悬架分块动力学模型的在线系统参数与外扰识别研究
2017-05-17郝慧荣张慧杰
郝慧荣, 张慧杰
(内蒙古工业大学 能源与动力工程学院, 呼和浩特 010051)
悬架分块动力学模型的在线系统参数与外扰识别研究
郝慧荣, 张慧杰
(内蒙古工业大学 能源与动力工程学院, 呼和浩特 010051)
根据汽车悬架动力学特性的理论知识,建立了七自由度汽车分块悬架动力学方程,车身分块系统中不包含路面外扰,故其辨识精度不会受外扰影响。推导了分块悬架动力学方程从惯性物理坐标到传感器坐标的变换。依据递推最小二乘算法,利用执行器作为激励,采用时域辨识方法对参数进行辨识,辨识出了从执行器到传感器的汽车分块悬架动力学模型。实现了悬架模型在线参数辨识与路面外扰反解识别,为七自由度汽车悬架的振动主动控制打下了坚实的基础。
分块悬架; 动力学模型; 参数辨识
汽车悬架系统对提高车辆操作稳定性和行驶平顺性起着至关重要的作用,现代高级轿车中主动悬架的应用越来越广泛,而实现良好的悬架振动控制效果的关键是能够获得准确的悬架动力学模型,尤其是在线参数模型[1-6]。关于在线参数辨识,文献[7]介绍了动力学系统辨识的递推最小二乘算法;文献[8]应用此算法辨识了六自由度主被动一体隔振平台,但有关悬架利用递推最小二乘算法辨识的国内外还很少研究;文献[9]给出了应用递推最小二乘算法辨识悬架参数,但没有考虑地面外扰对辨识的影响,而路面外扰很难监测,因此给出的方法不那么实用。
虽然整车悬架机构复杂,但其动力学模型,可采用了多刚体系统动力学的方法建立,模型参数采用实验建模的方法进行辨识。由于乘员与货物的变化,整车质量及其质心也会随之发生变化;悬架系统的弹簧、减振器及提供主动力的执行器都存在一定的非线性,从而使它们工作的平衡点位置随着汽车质量及其质心的变化而发生变化;再有车辆在行驶过程中,地面外扰始终存在,会对辨识精度产生影响,为此,这里提出一种对汽车悬架进行分块在线参数辨识的方法。
1 悬架整车动力学方程及其化简
对整车进行动力学分析时,可以将车身、车轮和车轴等看作刚体,悬架、车轮等看作弹簧和阻尼器;要实现悬架在线辨识及主动控制,为悬架弹簧并联一执行器,其两端布置传感器,如图1所示。图1(a)给出了七自由度整车悬架动力学模型,图中符号含义:z为车身垂向位移;θx为侧倾角;θy为俯仰角;vi为外扰激振输入(i=1,…,4下同);zui为车轮的位移;zi为车身与悬架连接点处的位移;ui为主动可控力;lxi、lyi为轮胎距离整车质心纵、横向距离。图1(b)将整车悬架分解成上面的“车身”三自由度系统与下面的4个“车轮”单自由度系统。对于“车身”,由于“传感器”和“执行器”的加入,使得它成为既是可观的也是可控的系统;而对于“车轮”,因其是单自由度系统,可以线下测试,获得先验信息。
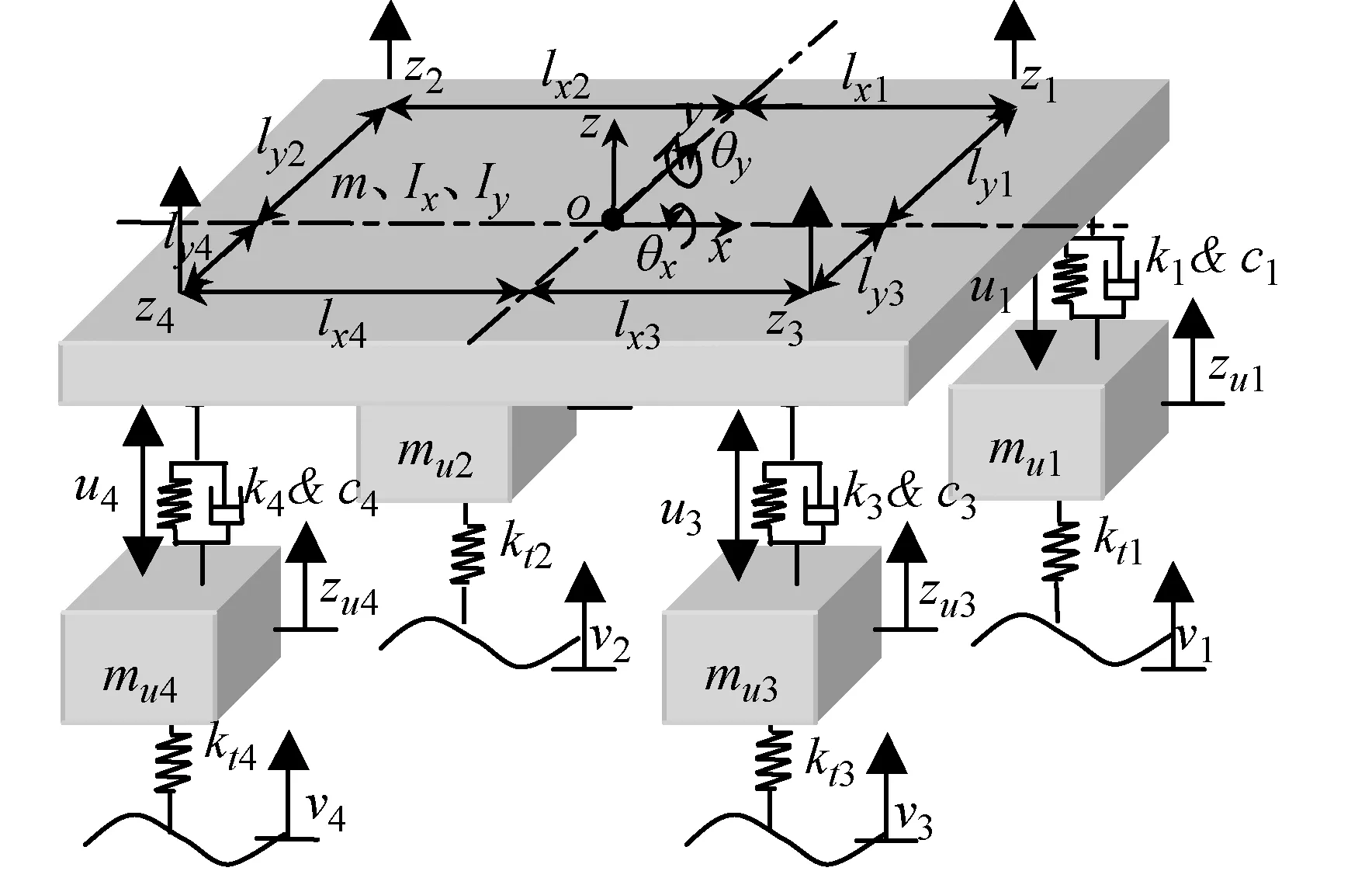
(a)

(b)
采用了多刚体系统动力学的方法,在惯性物理坐标系下,利用Lagrange方程汽车悬架整车动力学方程为
(1)
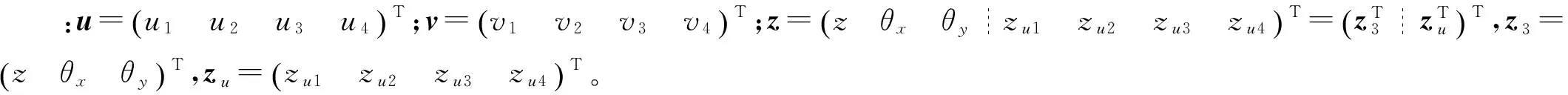

主动控制力矩阵E是力雅克比矩阵[10];阻尼矩阵与刚度矩阵有相似的结构,只是将“k”换做“c”,限于篇幅,后文都省去了阻尼矩阵。基于图1(b)的整车悬架分解,将式(1)按分块矩阵[11]可写为式(2a)和式(2b)的联立
式中:k=diag([k1k2k3k4]);K3=E3kE3;K3×4=E3k;Ku=k+kt。式(2a)表征非悬架质量以上的车身三自由度系统,式(2b)表征四个车轮单自由度系统,两者联立表征车辆悬架七自由度系统。
2 悬架在传感器坐标下的分块状态方程
为了实现悬架在线辨识与主动控制,下面推导式(2)在传感器坐标系下的形式。在侧倾角θx与俯仰角θy较小的情况下,车身与悬架连接的点zi线位移可以用z、θx、θy线性表示
(3)
若z1~z4的四个点中有三个点不同,由式(3)得
(4)
z3=(φT)-1w=(φ-1)Tw
(5)
z4=bTz3=bT(φT)-1w=bT(φ-1)Tw= (φ-1b)Tw=aTw
(6)
式(4)和式(5)表明从z1~z4的四个点中任选三个都可以表征车身三自由度,这里不失一般性选用z1、z2、z3。式(6)表明z4与z1、z2、z3线性相关,其中aT=(a1a2a3),不难证明a1+a2+a3=1。将式(5)代入式(2)得
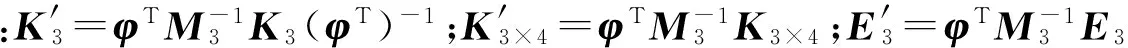
将式(6)和式(7)合在一起可写为

根据式(7)和式(8)可以方便写出其在传感器坐标系下的状态方程,即悬架分块状态方程
(9a)
(9b)

将式(8a)与式(8b)相加后得
(10)
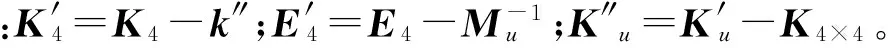
将式(3)和式(5)代入式(2),还可化简整理为

将式(11a)的三个方程加和在一起后得
(12)

3 分块动力学模型分析及递推最小二乘算法
在工程实际中对于悬架系统的参数辨识问题,更关心非悬架质量上的车体三自由度系统,即式(2a),这是因为汽车经常由于乘员与货物的变化使悬架动力学模型发生变化的正是这一部分,而轮胎刚度及非悬架质量通常不发生变化,在辨识前通过简单的测试就能知道。执行器的力是输入、传感器的位移是输出,根据图1(b)的模型、及式(2a)就能辨识出车身三自由度系统。
通过前文的推导可知道,式(7)~式(12)都是式(2)的一种线性变化形式,本质上它们等价,但又有区别:应用式(7a)可方便快捷的辨识车身三自由度系统参数,但其中k、c没有单独被辨识出来,它们都隐含在被辨识的参数当中;式(8)只是式(7)的增广形式,包含了式(6),利用式(7a)和式(8a)可方便给出悬架系统的分块状态方程式(9a)的参数;式(10)则是式(8a)与式(8b)相加后得到的,可理解成系统的合外力与合内力相平衡,可用其反解路面外扰;而式(11a)被应用于辨识车身系统参数k、c,但式(11a)的三个方程中有重复参数c4、k4,故使用式(12)进行辨识;若通过另外的测试知道车辆的非悬架质量Mu及轮胎刚度kt、阻尼ct等先验信息,辨识出k、c后利用式(8b)就能给出悬架系统的分块状态方程式(9b)的参数。
综上,悬架分块动力学方程的辨识关键在于对式(6)、式(7a)、式(12)中参数进行辨识,利用式(10)或式(11b)对路面外扰进行反解识别。
通过观察发现:式(6)的待辨识参数为1×3=3个,式(7a)的待辨识参数为3×18=54个,式(12)的待辨识参数为1×11=11个,总共待辨识参数为68个,而在文献[9]中不分块辨识的悬架动力学方程的待辨识参数为129个,可见利用悬架分块动力学方程再进行悬架参数在线辨识可以极大的减少计算工作量。
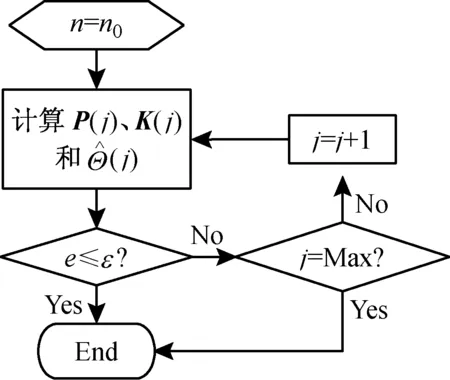
图2 递推算法流程图
4 悬架参数辨识仿真实例
这里给出一个悬架仿真辨识的实例,具体仿真参数为:m=876 kg,Ix=438 kg/m2、Iy=2 337 kg/m2;mu1=mu3=153 kg、mu2=mu4=85 kg;lx1=lx3=0.938 m、lx2=lx4=1.693 m;ly1=ly3=1.534 m、ly2=ly4=1.452 m;k1=k3=12 480 N/m、k2=k4=15 730 N/m;c1=c3=348 N·s/m、c2=c4=782 N·s/m;kt1=kt2=kt3=kt4=235 kN/m。仿真需要的信号包括致动器输入的力,传感器输出的位移、速度、加速度,工程实际中速度、加速度可以用位移数值微分一次、两次获得。将前面的仿真数据代入式(9),在Matlab中就能给出悬架分块状态方程,用Simulink为悬架建立仿真辨识模型,如图3所示。图3中“Clock”是辨识使用的同步时间模块;“Zero-Order Hold”是零阶保持采样模块,采样频率为1 000 Hz;“Eq9(a)、Eq9(b)”是根据式(9)给出的悬架分块状态方程模块;“u_v”是利用Matlab Function编制的控制信号和外扰信号模块,模拟现实中的主动控制力和路面激励;“Memory”是整时间步长的延迟模块,或可理解是数据暂存模块,它提供给递推程序上一次的辨识值、误差值;“RLSA”是根据递推最小二乘算法,利用Matlab Function编制的程序模块,模拟车辆ECU中的在线辨识器,RLSA模块的端口“e_、T_、P_”分别代表误差、辨识值、信息矩阵;端口“v_”代表辨识反解出的路面外扰;端口“D”是辨识数据的输入口;端口“I_D”是初始辨识数据的输入口。

图3 分块悬架辨识仿真模型
图4给出了应用递推最小二乘算法,辨识参数时的误差随时间变化曲线,误差收敛容许条件ε=10-4,可见参数的估计值是收敛的,图4中“e100、e500”的下角标分别代表初始观测次数n0=100、500(t=0.1 s、0.5 s)。图4(a)中e100从0.1~0.5 s历时0.4 s误差才收敛,e100最大绝对误差值达3×105;而图4(b)中e500从0.5~0.6 s历时0.1 s误差就收敛了,e500最大绝对误差值小于80,可见初始数据越多收敛速度越快,其最大绝对误差值也越小。

(a)(b)
图4 误差曲线
Fig.4 Curve of errors


(a)(b)
图5 辨识值与实际值对比
Fig.5 Contrast between identification value and real value
图6给出了实际输入路面外扰v与反解识别出的外扰v_的对比,其初始观测次数n0=100(t=0.1 s)。图6(a)是输入路面外扰是正弦信号,图6(b)是输入路面外扰是锯齿波信号。通过对比发现:t≤0.1 s时,辨识程序在准备初始观测数据,因此没有反解路面外扰;0.1 s
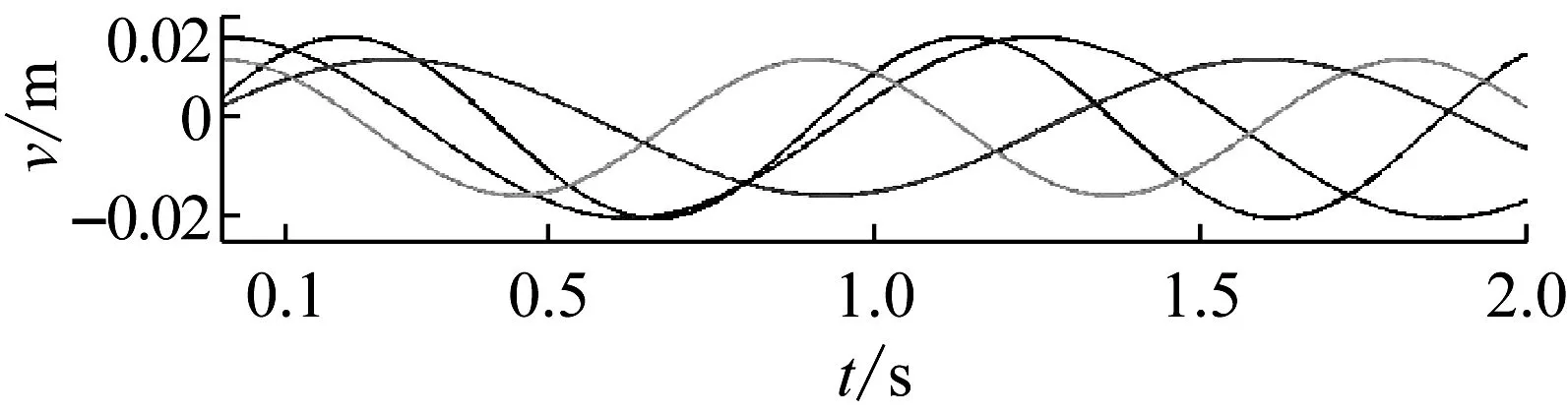
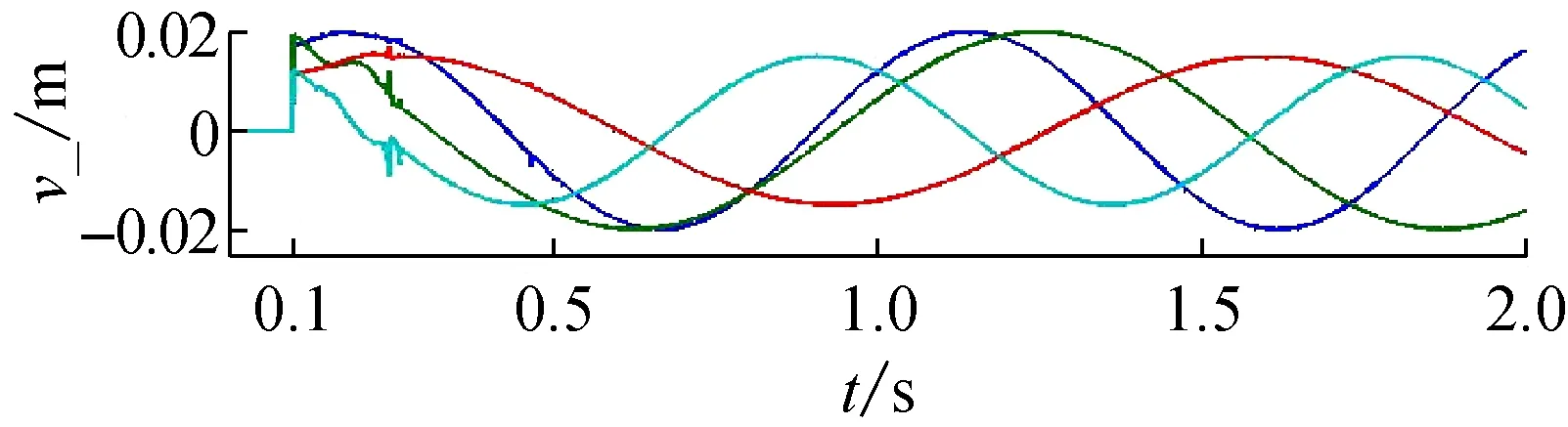
(a)
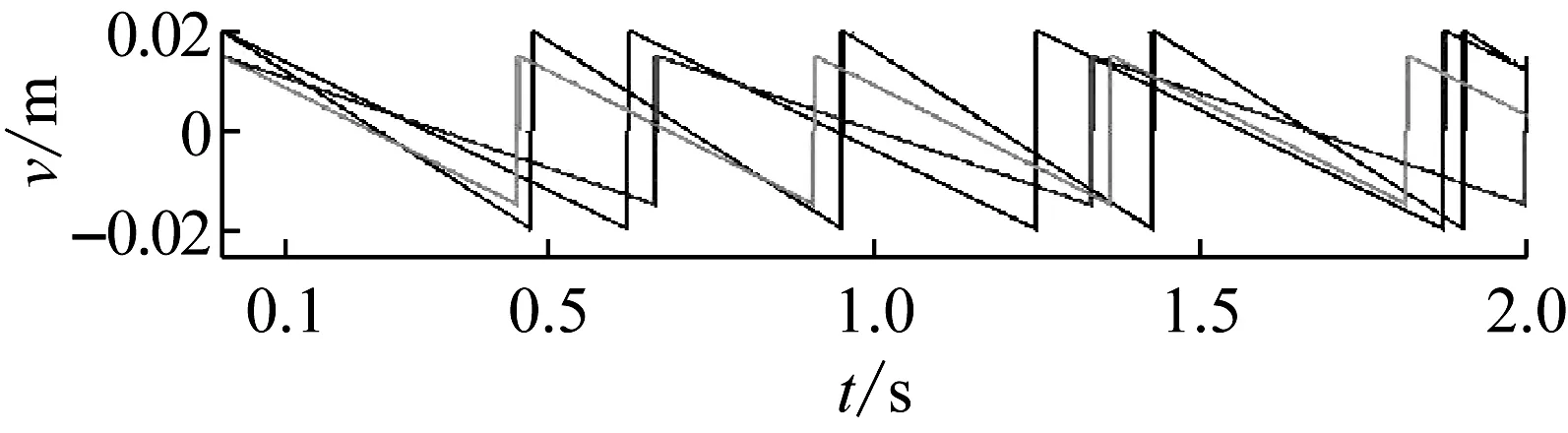

(b)
5 结 论
通过对悬架分块动力学模型在线参数的辨识研究得到如下结论:
(1) 悬架分块动力学模型的物理解释,“整车”悬架的七自由度动力学方程可以分解成上面的“车身”三自由度系统与下面的四个“车轮”单自由度系统。
(2) 在传感器坐标下所建立的悬架分块动力学方程为悬架模型的在线辨识提供了可用的先验知识。
(3) 悬架分块模型中的“车身”三自由度系统不再包含地面外扰,因此路面外扰不会影响模型精度,它既是可观的也是可控的;已知车辆的非悬架质量及轮胎刚度、阻尼,由四个“车轮”单自由度系统可反解路面外扰。
(4) 利用递推最小二乘算法进行参数在线辨识时,使用的初始数据越多则收敛速度越快,其最大的绝对误差值也越小。
[1] 周长城.汽车平顺性与悬架系统设计[M].北京: 机械工业出版社, 2011.
[2] 哈里斯C M,克瑞德C E. 冲击和振动手册[M].北京:科学出版社,1990.
[3] 刘伟,史文库,方德广,等. 汽车动力学分析及悬架子系统优化设计[J].哈尔滨工业大学学报, 2012,44(3):96-101.
LIU Wei, SHI Wenku, FANG Deguang. Vehicle dynamics analysis and optimization of suspension design[J].Journal of Harbin Institute of Technology, 2012, 44(3):96-101.
[4] 李彦,何琳,褚福磊,等.磁流变阻尼器实验建模及模糊半主动振动控制[J].振动与冲击,2009,28(11):91-96.
LI Yan, HE Lin, CHU Fulei. Modeling of MR-fluid damper and fuzzy semi -active vibration control strategy[J]. Journal of Vibration and Shock, 2009,28(11):91-96.
[5] 李中付,华宏星.一种非稳态环境激励下线性结构的模态参数辨识方法[J].振动与冲击,2008,27(3):8-12.
LI Zhongfu,HUA Hongxing. Modal parameters identification of linear structures undergo in non-stationary ambient excitation[J]. Journal of Vibration and Shock, 2008,27(3):8-12.
[6] 王斌,刘昭度,吴利军,等.汽车动力驱动系统传递特性实验建模[J].汽车工程,2007,29(2):137-140.
WANG Bin, LIU Zhaodu,WU Lijun,et al. Experimental modeling for transfer characteristics of automotive powertrain system[J]. Automotive Engineering, 2007,29(2):137-140.
[7] 刘君,夏智勋.动力学系统辨识与建模[M].长沙:国防科技大学出版社, 2007.
[8] 郝慧荣,白鸿柏,张慧杰,等.六自由度主被动一体隔振平台的动力学实验建模[J].振动与冲击,2011,30(11):4-7.
HAO Huirong, BAI Hongbai, ZHANG Huijie,et al.Experimental dynamic modeling of 6-DOF active-passive vibration isolation platform[J]. Journal of Vibration and Shock,2011,30(11):4-7.
[9] 张慧杰,郭志平,司景萍,等.汽车悬架整车动力学模型的参数辨识[J].振动与冲击,2013,32(23):145-150.
ZHANG Huijie, GUO Zhiping, SI Jingping, et al. Parametric identification of a vehicle suspension dynamic model[J]. Journal of Vibration and Shock, 2013,32(23):145-150.
[10] MACIEJEWSKI I. Control system design of active seat suspensions[J]. Journal of Sound and Vibration, 2012, 331(6):1291-1309.
[11] 高振兴. 矩阵的分块与应用[J].辽宁师范大学学报(自然科学版), 2011,34(2):157-161.
GAO Zhenxing. Block and application matrix[J]. Journal of Liaoning Normal University (Natural Science), 2011,34(2):157-161.
Online recognition of system parameters and external excitations for a vehicle block suspension dynamic model
HAO Huirong, ZHANG Huijie
(College of Energy and Power Engineering, Inner Mongolia University of Technology, Hohhot 010051, China)
According to the theory of a vehicle suspension’s dynamic characteristics, the dynamic equations were established for a vehicle block suspension with 7-DOF. There is no road disturbance in the vehicle body block system, so the identification precision was not affected by external excitation. These dynamic equations were converted from the inertial physical coordinates into the sensor coordinates. On the basis of the recursive least squares algorithm(RLSA), using actuators as excitations, the vehicle block suspension dynamic model was identified from actuators to sensors. The model parameters were recognized with time-domain identification method. Furthermore, the online parametric identification of a vehicle block suspension model and its road disturbances recognition were realized. The results laid a foundation for the vibration active control of a 7-DOF vehicle suspension.
block suspension; dynamic model; parametric identification
2016-05-18 修改稿收到日期:2016-09-07
郝慧荣 男,博士,讲师,1981年生
U463.33
A
10.13465/j.cnki.jvs.2017.09.033
