一种体外预应力钢筋混凝土摇摆框架抗震性能研究

鲁 亮， 刘 霞

(同济大学 结构工程与防灾研究所， 上海 200092)

一种体外预应力钢筋混凝土摇摆框架抗震性能研究

鲁 亮， 刘 霞

(同济大学 结构工程与防灾研究所， 上海 200092)

体外预应力摇摆框架(External Prestressing Rocking Frame，EPRF)是一种新型的采用结构控制技术的抗震结构体系。建立了单榀体外预应力摇摆框架的力学模型并推导其理论抗侧刚度公式；其次，建立了无阻尼耗能的体外预应力摇摆混凝土框架、有阻尼耗能的体外预应力摇摆混凝土框架以及常规钢筋混凝土框架的有限元模型；输入El Centro地震波采用ABAQUS有限元程序对三种框架进行了动力时程分析，得到了地震作用下的结构楼层位移响应、加速度响应和层间剪力响应，对比分析了三种框架的地震响应结果。研究结果表明，具有阻尼耗能的体外预应力摇摆框架能大幅度降低结构加速度和层间剪力响应，结构位移响应也能得到有效控制。

体外预应力； 摇摆框架； 力学模型； 时程分析； 抗震性能

Kurama等[1]将竖向无黏结预应力钢绞线引入摇摆结构，并且系统地研究了无黏结预应力混凝土自复位剪力墙的工作性能。Kurama等[2]针对这种自复位剪力墙提出了改进措施，增加了黏滞阻尼器，在侧向变形时能够耗能。为了提高摇摆体系的耗能能力，Ajrab等[3]提出了附加索缆系统，索缆通过撑杆与摇摆墙体在各楼层位置处相连, 并在索缆底部通过串联的阻尼器与基础相连。Restrepo等[4]对自复位剪力墙作出了进一步改进，在墙体与基础之间增加了一种软钢阻尼器在墙体产生一定的侧向变形时通过软钢的塑性变形来耗能。Eatherton等[5]研究了无黏结预应力技术应用于摇摆墙的结构体系，利用摇摆墙及其附属的阻尼耗能装置控制结构的变形模式和最大地震响应，并且实现了自复位功能。Deierlein等[6]提出由钢支撑框架、竖向后张预应力钢筋以及便于更换耗能元件组成的摇摆结构体系。

Lu等[7]提出受控摇摆式钢筋混凝土框架(Controlled Rocking Reinforced Concrete Frame, CR-RCF)这一新型抗震结构形式，并展开了一系列低周反复荷载和振动台试验研究[8-11]。这种新型结构体系的技术特征在于：① 放松柱与基础、柱与梁约束，采用纯铰接形式，并在梁柱构件内布置无黏结预应力筋提供弹性恢复力，这样结构抗侧刚度得到较大弱化，结构所受地震作用将大大减小，通过调整预应力筋的数量来控制结构的抗侧刚度；② 结构层间布置阻尼器，以耗散地震能量并控制结构地震响应位移；③ 节点处设置抗风和抗小震装置，以满足结构在风荷载和小震作用下的舒适度要求。研究结果表明，CR-RCF结构具有优异的抗震性能，主体结构在罕遇地震作用下可以做到不出现任何损伤，地震后破损的耗能装置可方便更换。图1给出了CR-RCF结构的振动台试验模型及节点构造图。

(a) 振动台试验模型

(b) 梁柱节点构造图

(c) 梁柱节点俯视图

1 EPRF结构简介

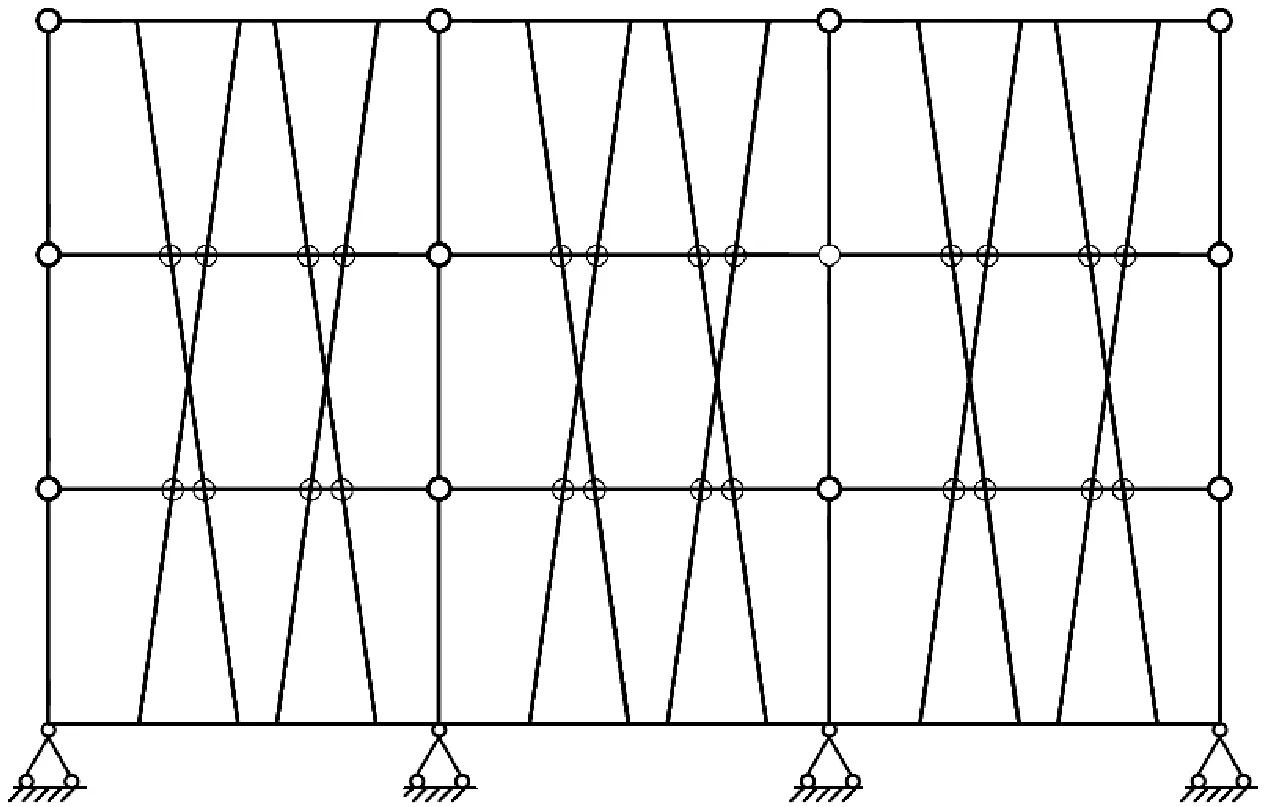
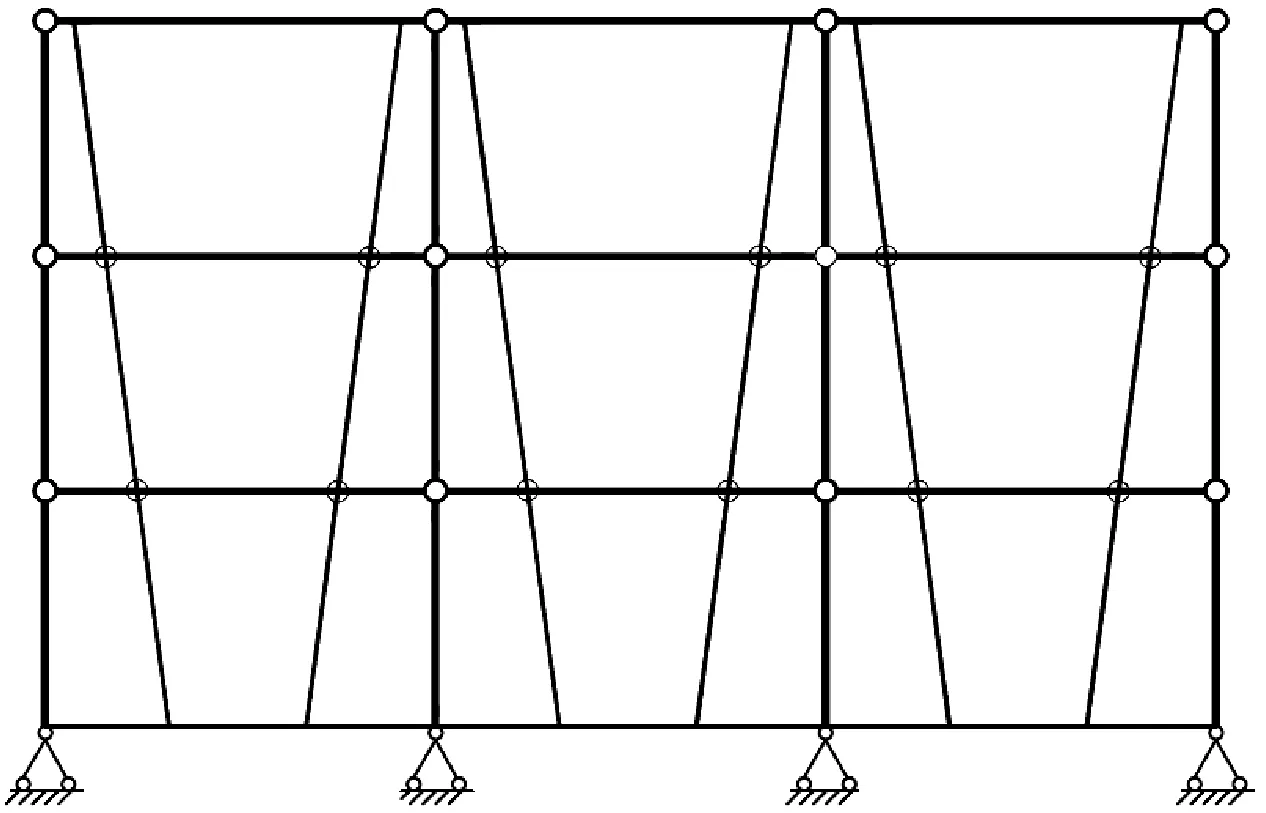
在大量调研国内外摇摆结构进展后，本文作者在受控摇摆式钢筋混凝土框架(CR-RCF)的基础上,首次提出了“体外预应力摇摆框架”(External Prestressing Rocking Frame，EPRF)这种新型抗震结构体系。与CR-RCF结构相比，EPRF结构具备CR-RCF所有结构控制技术特征，仅自复位恢复力提供方式不同。EPRF结构采用体外预应力提供地震作用下结构的自复位恢复力，体外预应力筋在一榀框架内对称且与竖向呈夹角布置，最初设想的结构竖向布置形式如图2所示。与CR-RCF结构相比，EPRF结构构造上的优点：① 体外预应力比体内施工方便，预应力控制简单；② 没有削弱梁柱构件截面。

预应力钢绞线提供恢复力，实现结构自复位，考虑到图2形式的预应力筋布置会在框架梁内产生较大的剪力和弯矩，为解决这个问题，图3给出了两种可能的预应力筋布置方案，中间层梁上下的钢绞线中预应力作用线在一条直线上，可以相互抵消大部分初始预应力，减小了由于预应力施加所带来的框架梁内力，仅需考虑对多层框架的顶层梁进行特别加强。在空间框架的另一方向，预应力筋的布置方式与图3所示类似，预应力筋布置空间受到建筑功能的限制，如与门窗、墙体位置冲突等，是工程实践的后续研究内容。与Kurama等提出的摇摆结构不同，EPRF结构预应力筋采用分段张拉形式锚固于相邻两层梁之间，并不采用整体张拉的方式。当然，体外预应力筋布置还可以有其它不同的布置方式。

图2 EPRF结构设想图

(a)

(b)

2 EPRF力学模型

2.1 理论刚度公式

EPRF结构通过在柱脚和梁柱节点设置纯铰节点来“弱化”框架结构的整体抗侧刚度，并通过梁间设置预应力钢绞线提供框架的整体水平恢复力，钢绞线通过预张拉产生初始张拉力，并保证在地震过程中不会出现零应力。初始张拉力由结构最大设计目标层间位移和水平抗侧控制刚度确定。地震作用下，结构发生摇摆，有效降低了地震作用下框架结构本身的延性设计需求；钢绞线在摇摆过程中受拉，产生的弹性恢复力保证框架结构在地震后恢复到初始位置。为阐明如此形式布置的预应力能产生水平恢复力以及得到恢复力模型，以下是推导过程，为分析方便，取一榀单层框架为例建立体外预应力摇摆框架的分析模型，如图4所示。

图4 EPRF结构的分析模型

在EPRF结构发生摇摆某一时刻，框架转过任意角度θ，实线为EPRF结构的初始状态，虚线为体外预应力摇摆框架发生摇摆后的状态，H为楼层高度，L1为钢绞线间距，d为钢绞线上下端锚固点间的相对距离，α为预应力钢绞线与柱的初始夹角，该参数由设计决定，β、β′分别为转动角度θ后两侧钢绞线转过的角度，N1，N2分别为框架柱的内力，F1，F2分别为预应力钢绞线的内力。

EPRF结构的运动模型可以表示为框架柱的运动为绕柱脚定轴转动，框架梁的运动为平动，则根据几何关系可得式(1)～式(8)

Hcosθ=(l+Δl1)cos(α+β)

(1)

d+Hsinθ=(l+Δl1)sin(α+β)

(2)

(3)

(4)

Hcosθ=(l-Δl2)cos(α-β′)

(5)

d=Hsinθ+(l-Δl2)sin(α-β′)

(6)

(7)

(8)

式中：l为预应力钢绞线初始长度；Δl1、Δl2分别为两侧预应力筋的变形量；F为作用在C点的水平推力，根据静力平衡原理，对A、B、C点取矩可得式(9)～式(11)

FHcosθ+N2Lcosθ+F2Lcos(α-β′)=0

(9)

FHcosθ-N1Lcosθ=F1Lcos(α+β)

(10)

F1dcos(α+β)+F2(L-d)cos(α-β′)+N2Lcosθ=0

(11)

设Δ=H·sinθ，由式(9)～式(11)可得式(12)

(12)

式中，kF为EPRF结构刚度。F1，F2又可以表示为

F1=Fp0+kpΔl1

(13)

F2=Fp0+kpΔl2

(14)

kp=EA/l

(15)

式中:Fp0为预张拉后钢绞线的初始力;kp为钢绞线的刚度;A为一侧钢绞线的面积;E为钢绞线的弹性模量。

根据式(12)可以得出EPRF结构的F-Δ的曲线，如图5所示，图中Δy为设计位移，Fy为钢绞线设计最大荷载，钢绞线初始预拉力Fp0=1/2Fy，当结构发生设计位移Δy时，B侧钢绞线松弛，初始预拉力完全释放恢复到0，结构中只有一侧钢绞线提供刚度；Δu为极限位移，Fu为极限荷载，当结构发生位移Δu时，钢绞线截面应力达到极限应力标准值。本结构设计的位移范围在-Δy～Δy范围内，Δy～Δu及-Δy～-Δu范围内整体结构刚度降低但一侧钢绞线仍能提供一定的刚度，作为结构的安全储备。

图5 体外预应力摇摆框架F-Δ预理论曲线

2.2 EPRF结构钢绞线角度

混凝土结构设计规范(GB 50010—2010)[12]规定在一般情况下，钢绞线张拉控制应力[σcon]不宜超过0.75fptk，fptk为钢绞线极限强度标准值。为确保EPRF结构始终处于弹性状态且预应力钢绞线具有一定安全余量，设计任一时刻钢绞线中的有效应力σe都不超过0.7fptk，结构在初始状态下钢绞线的应力为σi为0.35fptk，钢绞线变化的幅值Δσ，则摇摆过程中需满足式(16)

σi+Δσ≤0.70fptk

(16)

则Δσ≤0.35fptk，即

(17)

(18)

由于EPRF结构属于一种新型抗震结构体系，结构设计采用基于位移的设计方法，假如先设定层间位移目标设计值Δy，结构层高为H，则层间位移角tanθ=Δy/H，将式(17)、式(18)和θ值代入式(3)、式(7)可求得d值，由于tanα=d/H，可以求得α限值，即可确定钢绞线布置的角度。

本文中分析的一幢结构楼层高度3.6 m，钢绞线呈倒“八”字对称布置，，采用基于位移的设计方法，提出目标设计层间位移角最大值取tanθ=5%，即设计位移Δy=±90 mm，代入2.2节公式，可以求出钢绞线竖向布置角度α≤0.069，框架设计时取钢绞线与柱之间的夹角α=0.069。

2.3 结构刚度取值

EPRF结构的刚度和摇摆过程中的恢复力由体外预应力筋提供，而结构刚度的取值决定了结构动力特性和地震响应，EPRF结构刚度取值参考梁端铰型摇摆框架(CR-RCF)的取值原则。

经过试算，图3中EPRF结构刚度kF取为0.434 kN/m，单侧钢绞线可选用6根φs15.24标准型钢绞线。钢绞线的极限强度标准值fptk=1 860 N/mm2，弹性模量E=2.0×105MPa。

3 整体结构数值分析模型

采用ABAQUS有限元程序进行数值模拟。计算模型中梁柱及柱脚铰接接节点采用纯铰，预应力钢绞线的弹簧性能采用预拉Axial单元来模拟，X型阻尼器采用连接单元Cartesian模拟。试验模型中梁柱及人型支撑均采用梁单元B31模拟，单榀EPRF框架有限元模型示意图如图6所示。

图6 摇摆框架有限元模型示意图

考虑到常规钢筋混凝土框架结构在大震下构件进入塑性范围，梁柱材料模型采用混凝土塑性损伤模型，本模型中混凝土与钢筋本构采用同济大学基于ABAQUS开发的一组材料单轴滞回本构模型——TJ-Fiber[13]。

为了对比分析EPRF整体结构的动力特性及地震响应以评价其抗震性能，分别建立了常规框架RCF、EPRF无控结构(未设置层间耗能阻尼器)和EPRF有控结构(设置层间耗能阻尼器)三个有限元模型，建筑所在地区抗震设防烈度为8度，设计基本地震加速度为0.2g，设计地震分组为第三组，场地类别为Ⅲ类。计算结构原型为图7(a)所示三层框架结构，作为探索性研究，本文计算模型取其一部分(阴影部分)作单向水平地震激励动力响应分析。模型每层层高3.6 m，总高度10.8 m，纵向每跨跨度6 m，横向跨度6 m，框架平面布置如图7(b)所示。

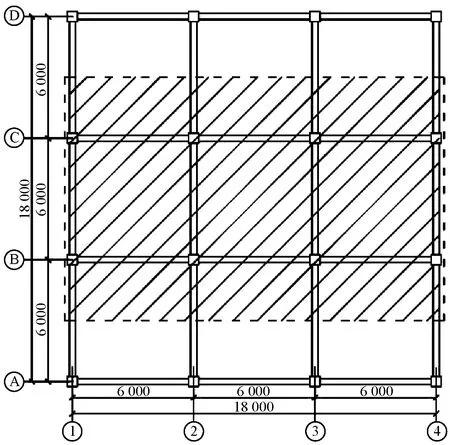
(a) 原型框架平面

(b) 计算模型平面尺寸

所有框架梁截面尺寸取300 mm×500 mm，柱截面尺寸取500 mm×500 mm，楼板板厚均为120 mm，楼面均布活荷载取2.0 kN/m2，混凝土密度为2 500 kg/m3，钢材密度为7 800 kg/m3，混凝土强度等级取为C40，钢筋强度等级均为HRB335。常规框架RCF的梁柱截面及配筋使用PKPM软件设计，EPRF无控及有控结构截面尺寸同常规框架RCF，配筋符合建筑抗震设计规范[14]梁柱构造要求。计算得到各层重力荷载代表值由下至上分别为1 053 kN、1 053 kN、963 kN。

本文EPRF整体结构层间位移角设计目标限值取为5%，结构的钢绞线与柱的初始夹角α的设置、整体结构刚度取值见本文第3节，为控制EPRF结构层间位移，在结构层间合理设置阻尼器(即EPRF有控结构)，布置在每层中间两榀框架平面内，共布置6个阻尼器，则EPRF整体结构每层钢绞线及阻尼器设置参数见表1。

参考本节中有限元的建模方法建立常规框架RCF和摇摆框架EPRF无控结构、EPRF有控结构有限元模型，三个模型如图8所示。

表1 EPRF结构钢绞线及阻尼器参数

(a) 常规框架

(b) EPRF无控结构

(c) EPRF有控结构

通过有限元计算结果，常规框架与EPRF无控结构、EPRF有控结构在X方向上的结构基本周期为：常规框架1阶周期为0.315 s，EPRF有控结构1阶周期为1.520 s，EPRF无控结构1阶周期为2.618 s，RCF结构周期最短抗侧刚度最大而EPRF无控结构周期最长结构抗侧刚度最小；EPRF有控结构相比于EPRF无控结构，由于结构层间设置了阻尼器，结构抗侧刚度有所提高，周期有所减小。粗略根据抗震规范设计反应谱曲线，结构周期变大(大于场地土特征周期)则结构地震响应加速度会相应变小、楼层剪力也会相应减小，可以认为EPRF结构具有较好的减震效果。

4 EPRF结构的抗震性能分析

本文分析所选地震动加速度时程是目前国内外经常使用的El Centro波，El Centro波是1940年美国IMPERIAL山谷地震记录，最大加速度：南北方向341.7 cm/s2，东西方向210.1 cm/s2，竖直方向206.3 cm/s2，场地土属于Ⅱ类～Ⅲ类。

将El Centro波地震动时程输入到第3节所建立的RCF结构、EPRF无控和EPRF有控结构三个有限元模型中，输入加速度峰值分别取0.07g、0.2g、0.4g三种工况，分别对应于8度抗震设防烈度下的小震(众值烈度)、中震(设防烈度)和大震(罕遇烈度)三种工况，得到结构楼层位移、加速度响应和层间剪力响应。

4.1 EPRF结构的位移响应

RCF、EPRF无控结构和EPRF有控结构在三种工况下的楼层位移响应最大值如表2所示，表中位移单位为mm。

表2 结构位移响应

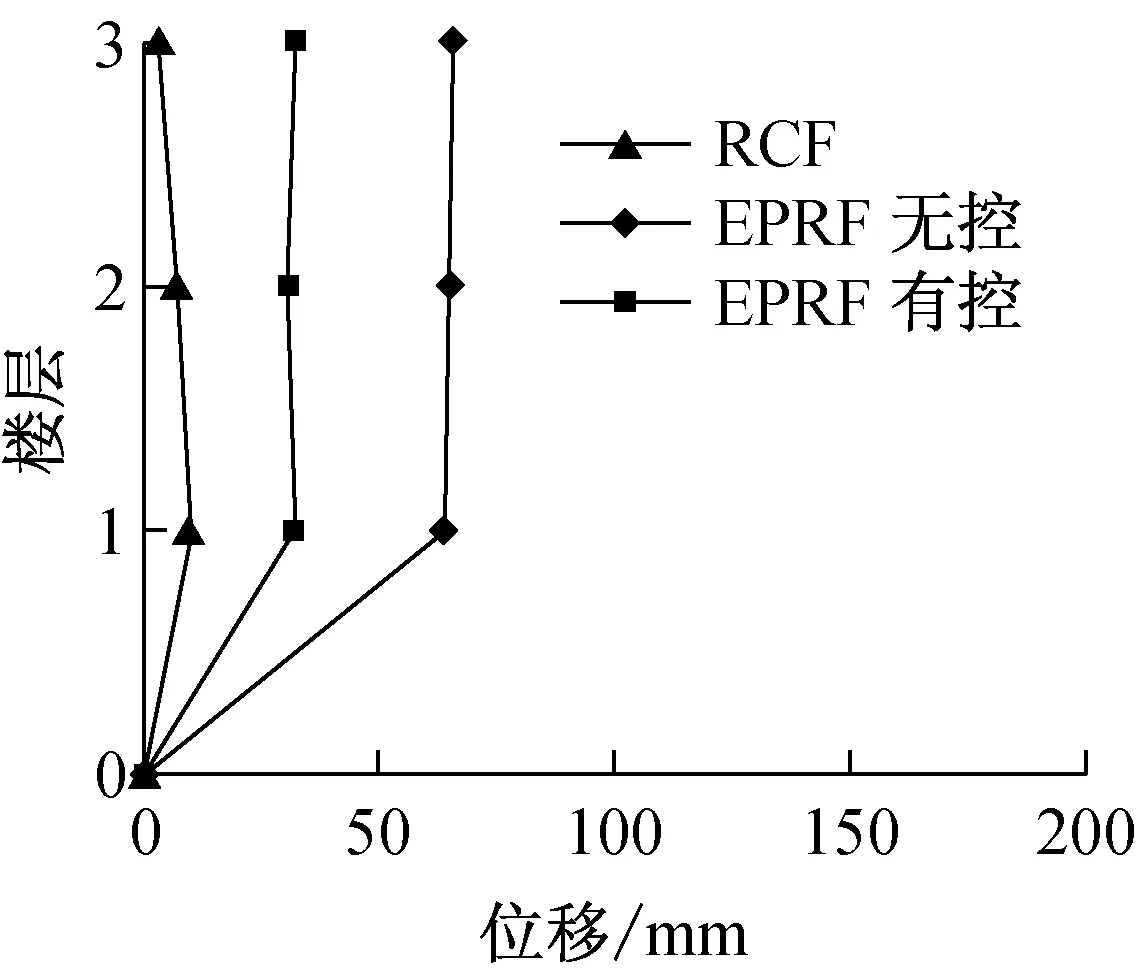
由表2可得到常规框架、EPRF无控结构和EPRF有控结构在小震、中震和大震三种工况下层间位移如图9所示。

(a) 小震

(b) 中震

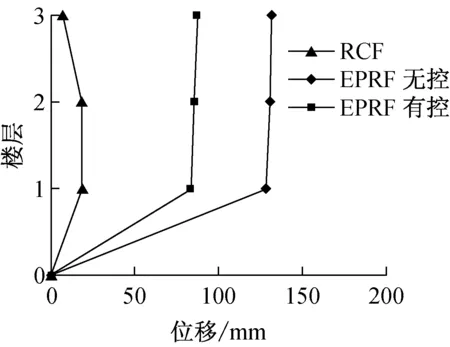
(c) 大震

由图9可知，在同等水准地震作用下，EPRF无控结构和EPRF有控结构的楼层位移远大于常规框架；由于EPRF有控结构中加入了层间阻尼器，结构位移显著得到控制，大震作用下，EPRF无控结构顶层的最大位移为389.5 mm，但是安装金属阻尼器装置后，位移下降为255.8 mm，位移减少了约34%，说明层间金属阻尼器的合理设置，能有效地控制结构的位移，从图9(c)可以看出大震下最大层间位移角为2.4%，小于5.0%的控制目标，即大震下钢绞线依然处于设定的弹性工作范围内。

4.2 EPRF结构加速度响应

RCF、EPRF无控和EPRF有控结构在三种工况下的加速度响应最大值如表3所示，为了便于比较，表3采用动力放大系数对比三种结构的加速度响应，图10给出了加速度放大系数对比图。

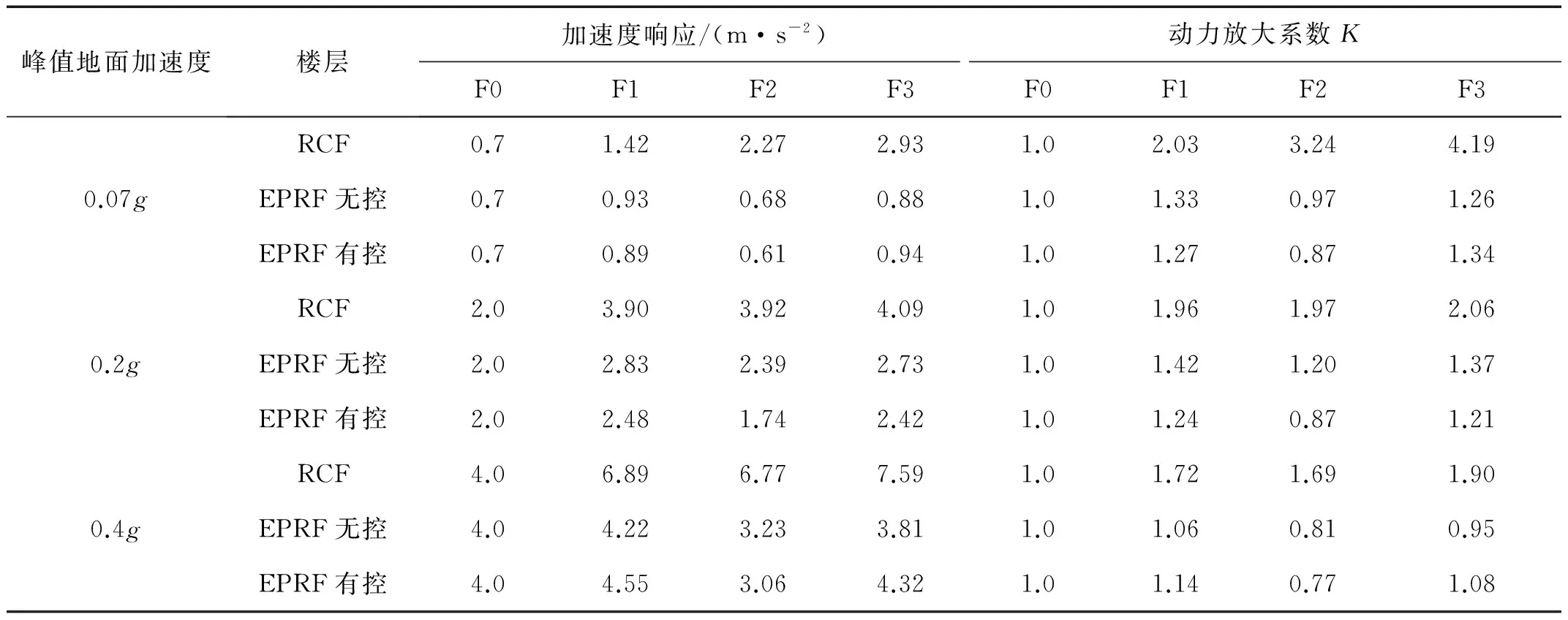
表3 结构加速度响应与动力放大系数K

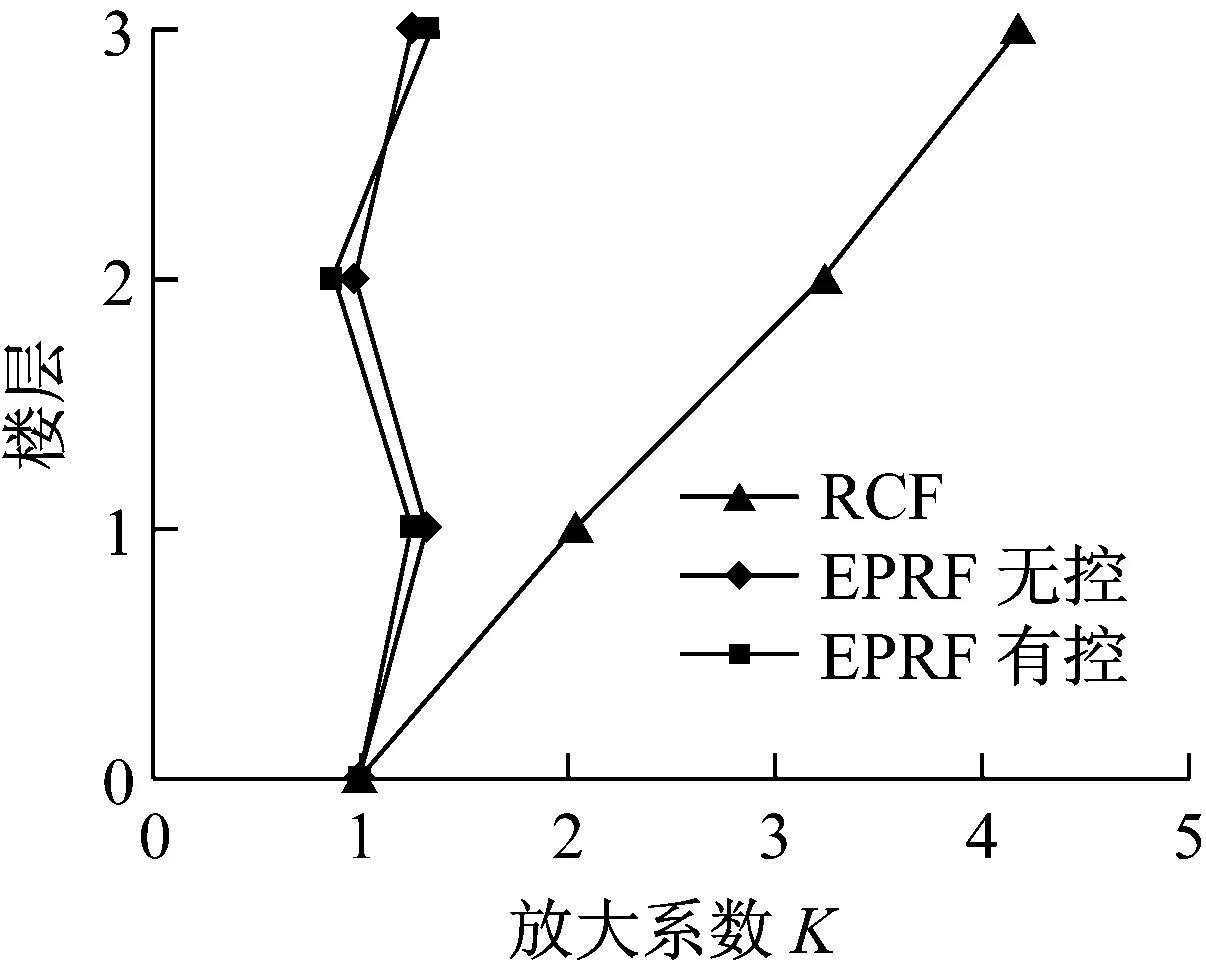
(a) 小震

(b) 中震

(c) 大震

4.3 EPRF结构的层间剪力响应

RCF、EPRF无控结构和EPRF有控结构在不同工况下的楼层剪力响应如表4所示，表中层间剪力的单位为kN。

表4 结构层间最大剪力响应

图11为结构层间剪力图，由图11可知，EPRF无控结构、EPRF有控结构中的层间剪力均大幅减小，其中EPRF无控结构柱基底剪力在小震、中震及大震作用下，比RCF结构减少了67.9%、55.7%、49.4%；EPRF有控结构基地剪力在小震、中震及大震作用下，比RCF结构减少了59.2%、57.8%、45.9%。

(a) 小震

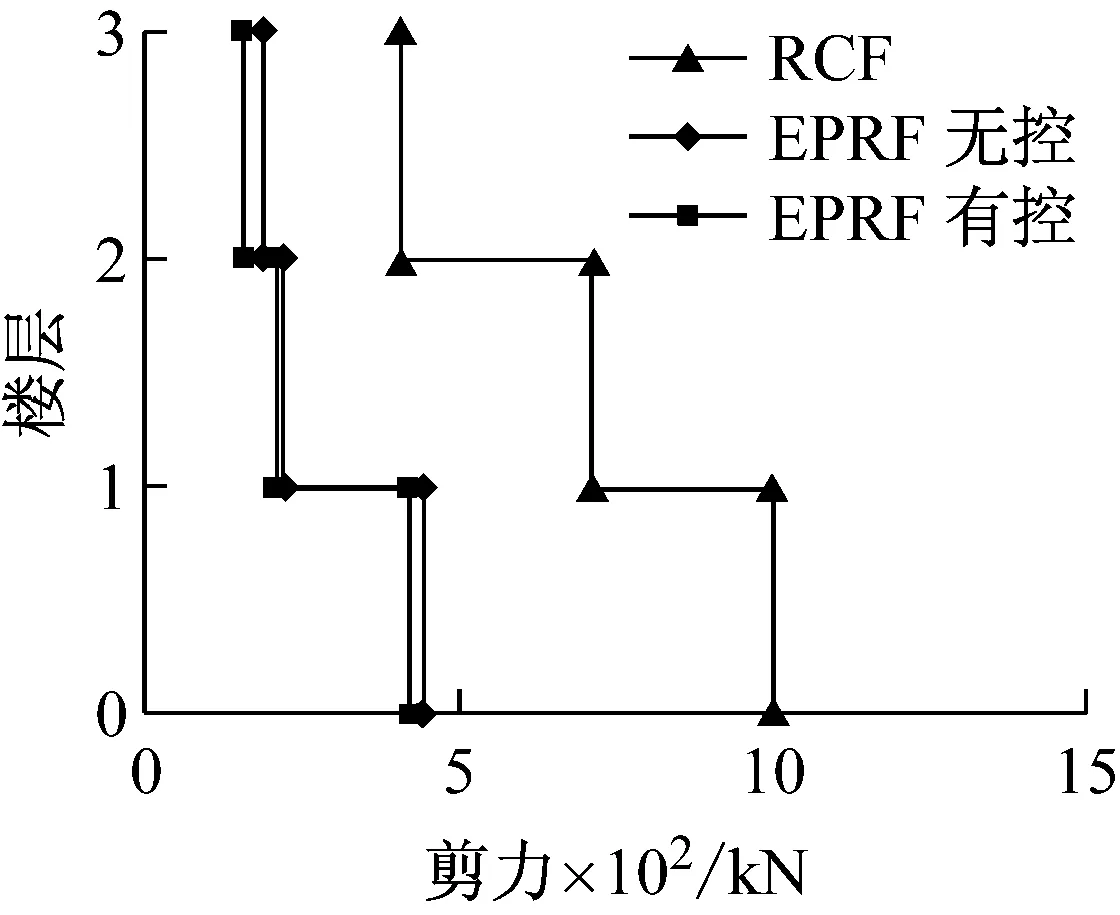
(b) 中震

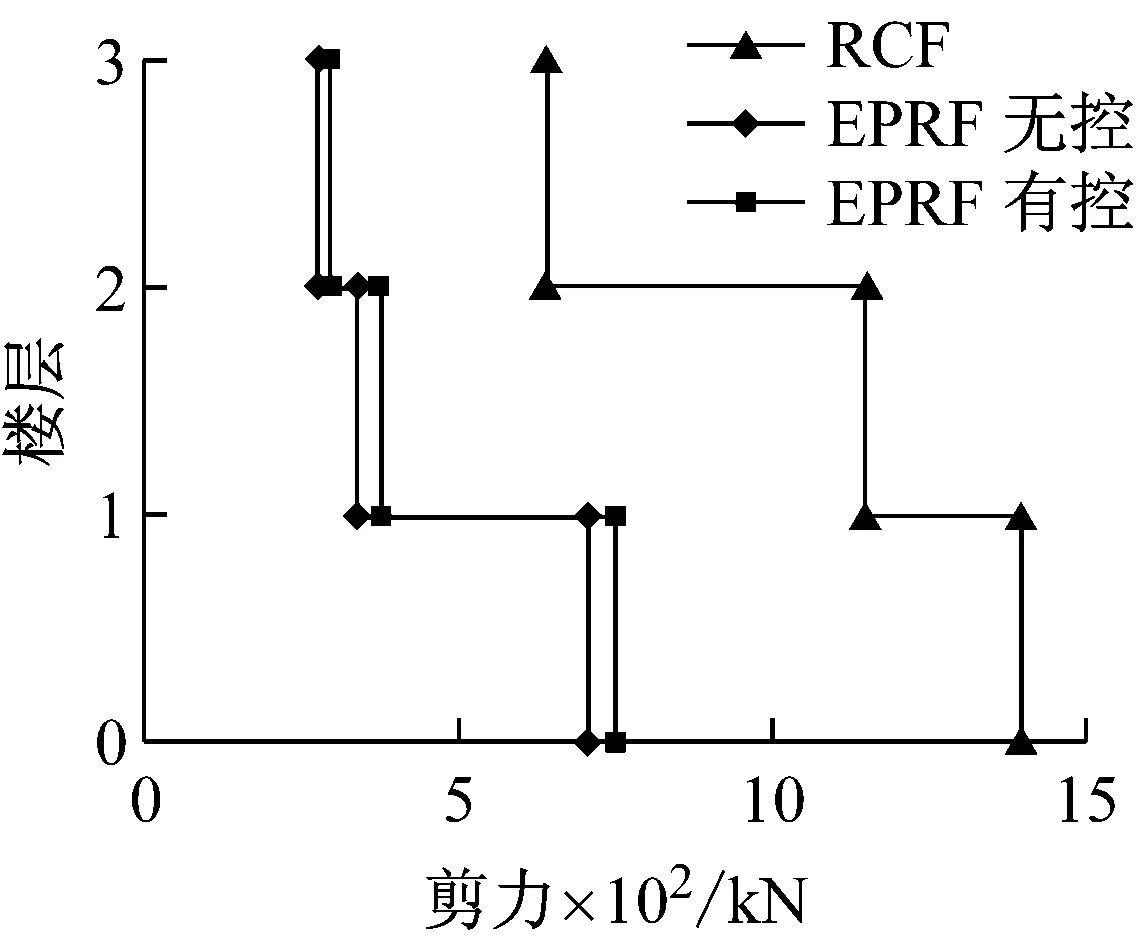
(c) 大震

5 结 论

本文提出了体外预应力摇摆框架(EPRF)新型抗震结构体系，建立了EPRF结构的力学模型并推导了抗侧刚度公式，通过ABAQUS软件建立了EPRF无控结构、EPRF有控结构和常规框架RCF的有限元模型，并分析了三种结构的抗震性能，可以得到以下结论：

(1) 与常规框架相比，EPRF结构(无控结构及有控结构)节点均采用铰接构造，结构整体抗侧刚度降低，结构自振周期增大，减震效果明显。

(2) EPRF有控结构相比于EPRF无控结构，结构中设置的层间阻尼器可以合理控制结构位移。

(3) EPRF结构在地震作用下的加速度响应及层间剪力响应显著减小。地震响应减小可以使得结构承受更大的地震作用，或者在相同的设防目标下，EPRF结构的构件承载力可以设计得更小，具有更好的经济性。

[1] KURAMA Y, SAUSE R, PESSIKI S, et al. Lateral load behavior and seismic design of unbounded post-tensioned precast concrete walls[J]. ACI Structural Journal, 1999, 96(4): 622-633.

[2] KURAMA Y C. Seismic design of unbounded post-tensioned precast concrete walls with supplemental viscous damping[J]. ACI Structural Journal, 2000, 97(4): 648-658.

[3] AJRAB J J, PEKCAN G, MANDER J B. Rocking wall-frame structures with supplemental tendon systems[J]. Journal of Structural Engineering, 2004, 130(6):895-903.

[4] RESTREPO J I, RAHMAN A. Seismic performance of self-centering structural walls incorporating energy dissipaters[J]. Journal of Structural Engineering, 2007, 133(11): 1560-1570.

[5] EATHERTON M, HAJJAR J F, DEIERLEIN G G, et al. Controlled rocking of steel-framed buildings with replaceable energy-dissipating fuses[C]//Proceedings of the 14th World Conference on Earthquake Engineering. Beijing: [s.n.], 2008: 12-17.

[6] DEIERLEIN G G, HAJJAR J F, EATHERTON M, et al. Seismically resilient steel braced frame systems with controlled rocking and energy dissipating fuses[C]//Network for Earthquake Engineering Simulation 7th Annual Meeting. Hawaii: [s.n.], 2009: 23-25.

[7] LU L, LU X L, ZHU F B, et al. Experimental study on seismic performance of a controllable rocking reinforced concrete frame[C]//Proceedings of the 5th International Conference on Advances in Experimental Structural Engineering. Taipei: [s.n.], 2013: 8-9.

[8] LU Liang, CHEN Junjie, LU Xilin. Numerical analysis of the seismic performance of a controllable rocking reinforced concrete frame[C]//Proceedings of the 13th International Symposium on Structural Engineering. Hefei: [s.n.], 2014: 24-27.

[9] 鲁亮，樊宇，刘亮,等. 受控摇摆式钢筋混凝土框架抗震机理研究[J]. 地震工程与工程振动，2015，34(1)：66-76.

LU Liang, FAN Yu, LIU Liang, et al. Research on the seismic performance of controlled rocking RC frame[J]. Journal of Earthquake Engineering and Engineering Dynamics, 2015, 34(1): 66-76.

[10] 鲁亮，刘霞，陈俊杰,等. 一种摇摆式钢筋混凝土框架节点刚度取值研究[J]. 振动与冲击，2015，34(13)：195-199.

LU Liang, LIU Xia, CHEN Junjie, et al. Parameter research of joints stiffness in a rocking reinforced concrete frame[J]. Journal of Vibration and Shock, 2015, 34(13): 195-199.

[11] 鲁亮，江乐，李鸿,等. 柱端铰型受控摇摆式钢筋混凝土框架抗震性能的振动台试验研究[J]. 振动与冲击，2016, 35(4): 193-198.

LU Liang, JIANG Le, LI Hong, et al. Shaking table test study on the seismic performance of a controllable rocking reinforced concrete frame with column-end-hinge joints[J]. Journal of Vibration and Shock, 2016, 35(4): 193-198.

[12] 混凝土结构设计规范: GB 50010—2010[S]. 北京：中国建筑工业出版社，2012.

[13] 吴晓涵. NosaCAD模型转ABAQUS模型说明书[EB]. http://www.nosacad.com/xzzx.htm.

[14] 建筑抗震设计规范: GB 50010—2011[S]. 北京：中国建筑工业出版社，2012.

Aseismic performance of an external prestressed rocking reinforced concrete frame

LU Liang， LIU Xia

(Research Institute of Structural Engineering and Disaster Reduction, Tongji University, Shanghai 200092, China)

A new seismic-resistance structure called the external prestressed rocking frame (EPRF) using the structure-control technology was proposed. Firstly, the theoretical lateral-resistance stiffness formula for a single frame of EPRF structures was derived based on its mechanical model. Then, three finite element analysis models were built for comparative analysis, they were an EPRF without dampers, an EPRF with dampers and a conventional frame. Finally, the seismic responses of the three frames including story drifts, story accelerations and inter-story shear forces were calculated with ABAQUS software using the time-history dynamic analysis and inputing the ground motion of El Centro earthquake wave. The comparison results showed that the EPRF structure with energy-dissipating dampers can greatly reduce the structural story accelerations and inter-story shear forces, and the structural displacement responses can be controlled effectively.

external prestressed; rocking frame; mechanical model; time-history analysis; aseismic performance

国家自然科学基金项目(51678453); 国家自然科学基金委国际合作项目(51261120377)

2015-11-06 修改稿收到日期：2016-03-29

鲁亮 男，博士，副教授，1969年生

TU352.1

A

10.13465/j.cnki.jvs.2017.09.027