杯形工具复合变幅杆设计及振动特性分析

陈汇资， 赵 波， 赵金坠，2， 高国富

(1. 河南理工大学 机械与动力工程学院, 河南 焦作 454000； 2. 郑州磨料磨具磨削研究所有限公司, 郑州 450007)

杯形工具复合变幅杆设计及振动特性分析

陈汇资1， 赵 波1， 赵金坠1，2， 高国富1

(1. 河南理工大学 机械与动力工程学院, 河南 焦作 454000； 2. 郑州磨料磨具磨削研究所有限公司, 郑州 450007)

针对硬脆材料曲面加工过程中加工精度差、效率低、加工费用高的问题，结合理论分析与有限元法，设计了一种适用于硬脆材料曲面高精度加工的超声杯形工具复合变幅杆。对所设计的变幅杆进行了阻抗特性分析和振动性能测试，结果显示变幅杆结构合理、振动效果良好；并通过有限元与试验的对比分析，探究杯形头的壁高、底厚、内径对杯形工具复合变幅杆谐振频率的影响。结果表明：变幅杆谐振频率随着底厚的增加而增大，随着杯形头壁高、内径的增大而减小，且实测结果与仿真分析较好符合。

硬脆材料;曲面加工;杯形工具复合变幅杆;有限元;谐振频率

随着曲面光学元件在航空航天、太空望远镜等高精尖设备上的广泛应用，对于硬脆材料曲面加工技术的需求也越来越迫切[1-2]。目前光学零部件等硬脆材料曲面加工常用的方法主要有精密磨削、研磨、抛光，不仅加工精度差，而且效率低、加工费用高。大量文献表明，可采用超声磨削加工技术解决上述问题，超声磨削技术相对于传统曲面加工技术具有以下优势[3-7]：① 超声磨削技术特别适用于脆硬材料的加工；② 超声磨削加工主要依靠磨粒瞬时局部的冲击作用来去除工件材料，因此切削力、切削热较小，大大减少工件的变形和烧伤现象，表面粗糙度也较低；③ 由于其工具头可根据零部件的形状做成相对应的成型加工工具，不需要工具头与工件做复杂的相对运动，就能完成复杂曲面的加工，从而提高了加工效率；④ 超声加工机床制作简单，只需要在普通精密机床上附加超声振动装置，拆卸、维修方便，不影响机床的非超声加工，降低了设备费用。

在加工硬脆材料的高精度平面和曲面时，需要采用大尺寸平面砂轮或杯状砂轮辅助超声振动的方法获得，其超声辅助磨削加工示意图(见图1)，装置主要包括:刀柄、电磁感应盘、带有杯形加工工具的复合变幅杆，本文将重点阐述杯形工具复合变幅杆设计及其振动特性。杯形工具复合变幅杆由于其截面形式复杂，所以声波在杆中的传导也异常复杂，耦合振动形式较多。因此，近年来国内外只有少数学者从事相关研究。许龙等[8]根据弯曲振动和耦合振动理论，设计了一种由变幅杆、薄圆盘和耦合振动圆筒组成的超声焊接振动系统，并且试验验证了在大信号测试条件下的纵-弯-纵振动模式。皮钧等[9]基于回形变幅杆的结构特点和纵波传播特性分析了波在变幅杆圆盘中发生的模态变化，发现了圆盘部分振动以切向振动模态为主，耦合后又转换为纵波形式。然后，基于三维波动方程建立了纵波回形变幅杆的频率方程，并且试验结果与理论结果基本吻合。笔者在前人工作的基础上，结合项目对零部件曲面加工质量及精度的特殊要求，设计了25 kHz杯形工具复合变幅杆，并在杯形头输出端或外壁圆周上电镀金刚石颗粒以供加工之用。

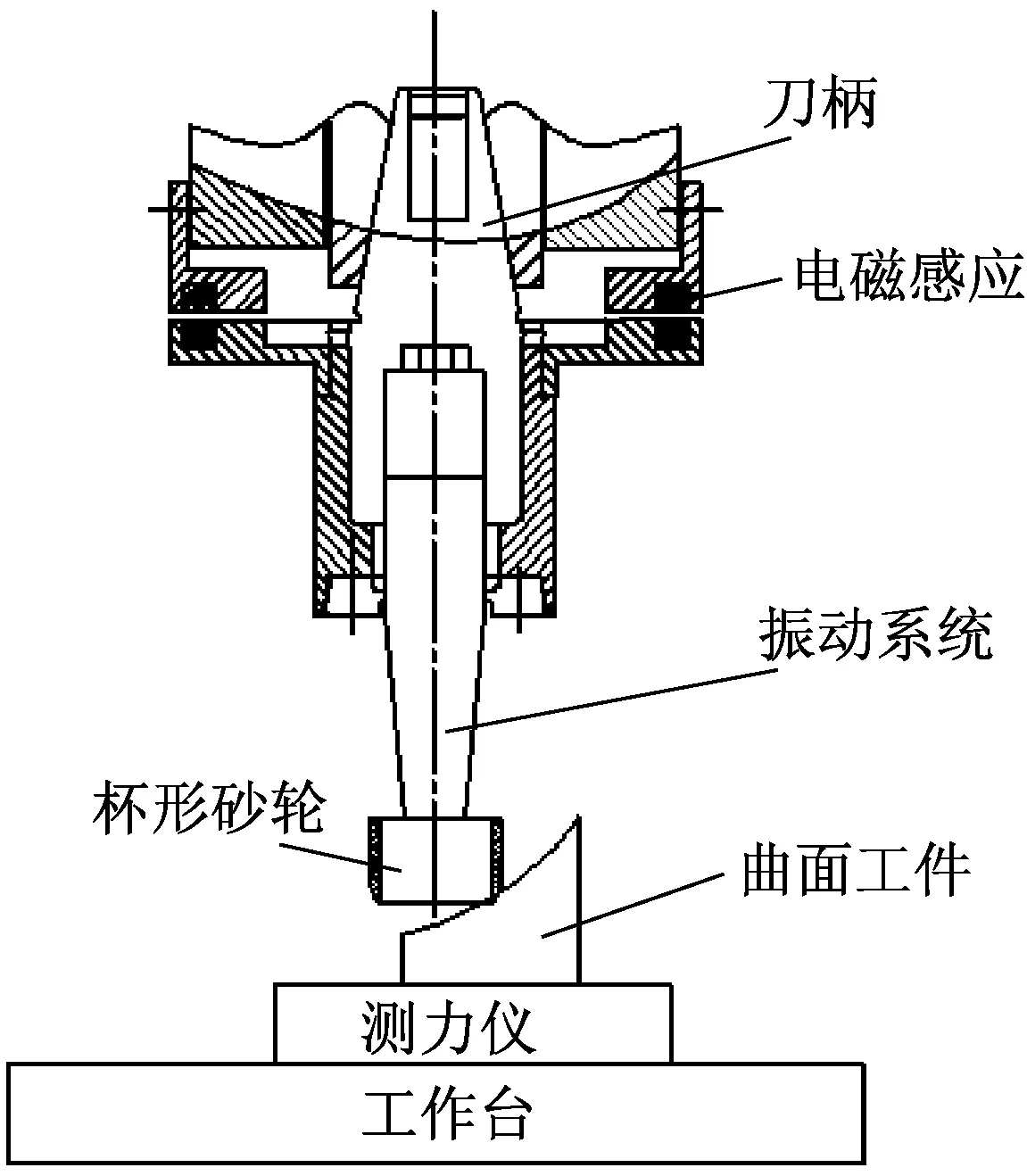
图1 超声铣磨系统工作的原理

1 杯形工具复合变幅杆的理论设计

由于杯形工具复合变幅杆振动形式异常复杂，目前尚没有权威的理论解释，为了更好深入研究这种异形结构，如图2所示。本文将杯形工具复合变幅杆分成简支边界薄圆板、圆筒和圆柱圆锥复合变幅杆三部分,分别应用薄板弯曲振动理论、耦合振动理论、一维纵向振动理论进行设计。

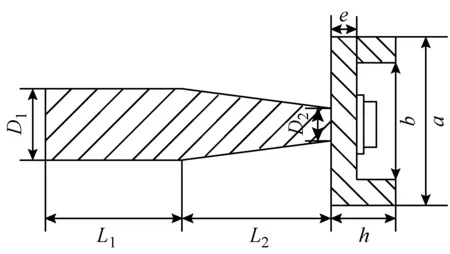
图2 变幅杆和杯形头

1.1 薄圆板理论设计

当圆盘的半径a远远大于其厚度e时，定义此圆盘为薄圆盘，根据弹性理论和薄板弯曲振动理论，薄圆盘的弯曲振动位移可表示为[10-12]

ξ(r,t)=[AJ0(knr)+BI0(knr)]exp(jωt)

(1)

弯矩和横向剪切力可表示为

Mr=-A[σJ1(knr)+knaJ0(knr)-

J1(knr)]+B[σI1(knr)+

knrI0(knr)-I1(knr)]

(2)

Qr=AJ0(knr)+BI0(kr)

(3)

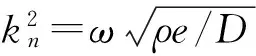
在简支边界条件下，弯曲振动薄圆盘的弯矩和横向剪切力皆为0，经对式(2)和式(3)整理后可求得薄圆盘的共振频率方程为

(4)

当薄圆盘的材料参数和几何尺寸给定时，代入式(4)，便可推出薄圆盘的共振频率为

(5)

1.2 圆筒耦合理论设计

当大直径圆筒受到纵向波激励时，由于泊松效应会产生径向振动，这时整个圆筒的振动是一个复杂的三维纵径耦合振动，难以求得能描述其振动形式的解析解。为了简化分析，本文只考虑纵向和径向振动，当引入等效弹性常数和等效机械耦合系数后，其振动可以等效成纵向和径向伸缩振动[13]。

根据圆筒的边界条件且忽略剪切力和应变，经过理论推导可得出圆筒的径向和纵向耦合振动频率方程为

(6)

sin[kz(h-e)]=0

(7)

式中:kr和kz分别为圆筒等效径向和等效纵向波数，为等效机械耦合系数；a、b分别为圆筒的外径、内径。式(6)和式(7)给出了圆筒耦合振动时的材料参数、几何尺寸、谐振频率之间的相互关系。当材料参数、几何尺寸给定时，即可求解径向和纵向耦合谐振频率。

1.3 圆柱圆锥复合变幅杆理论设计

由于圆柱圆锥复合变幅杆设计及运算较为常见，因此不再做详细阐述。该复合变幅杆通过传输矩阵法便可求得变幅杆频率方程为

(8)

式中:L1为变幅杆大端圆柱段长度;L2为圆锥段段长度;α为圆锥段截面变化系数，α=(N-1)/NL2。

2 有限元分析

通过PROE软件对薄圆盘、圆筒、变幅杆进行三维建模，然后将其模型导入到ANSYS中进行有限元分析。利用Solid 95单元划分有限元网格，选用Block Lanczos法对自由状态下的变幅杆进行模态分析，并在求解器提取的各阶模态中，选取与设计频率最为接近的谐振模态。

由于超声振动系统需安装到机床主轴上做高速旋转运动，为降低大尺寸工具的回转惯量，杯形头应采用较轻的材料。此外，变幅杆在工作过程中要承受一定的轴向和径向力，因此变幅杆应具备较大的轴向和径向刚度。基于上述要求，变幅杆、螺栓、垫片均采用45#钢，杯形砂轮采用6070铝合金，具体材料参数如表1所示。

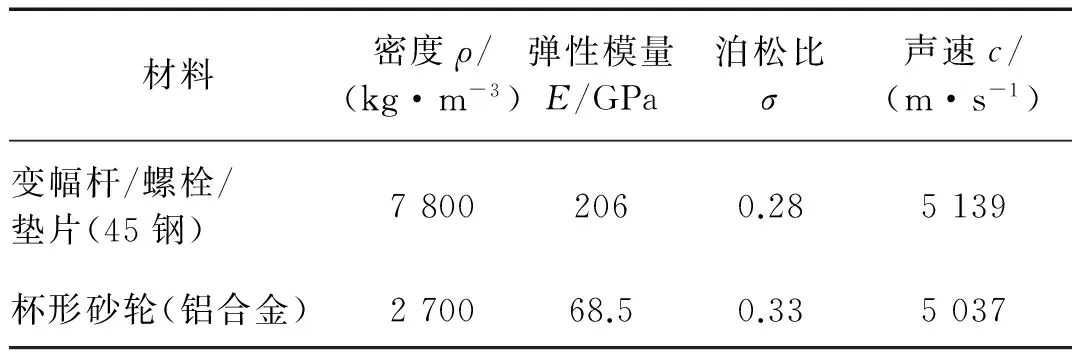
表1 材料参数

结合理论计算与有限元分析对杯形工具复合变幅杆进行设计及有限元修正，具体总设计流程，如图3所示。

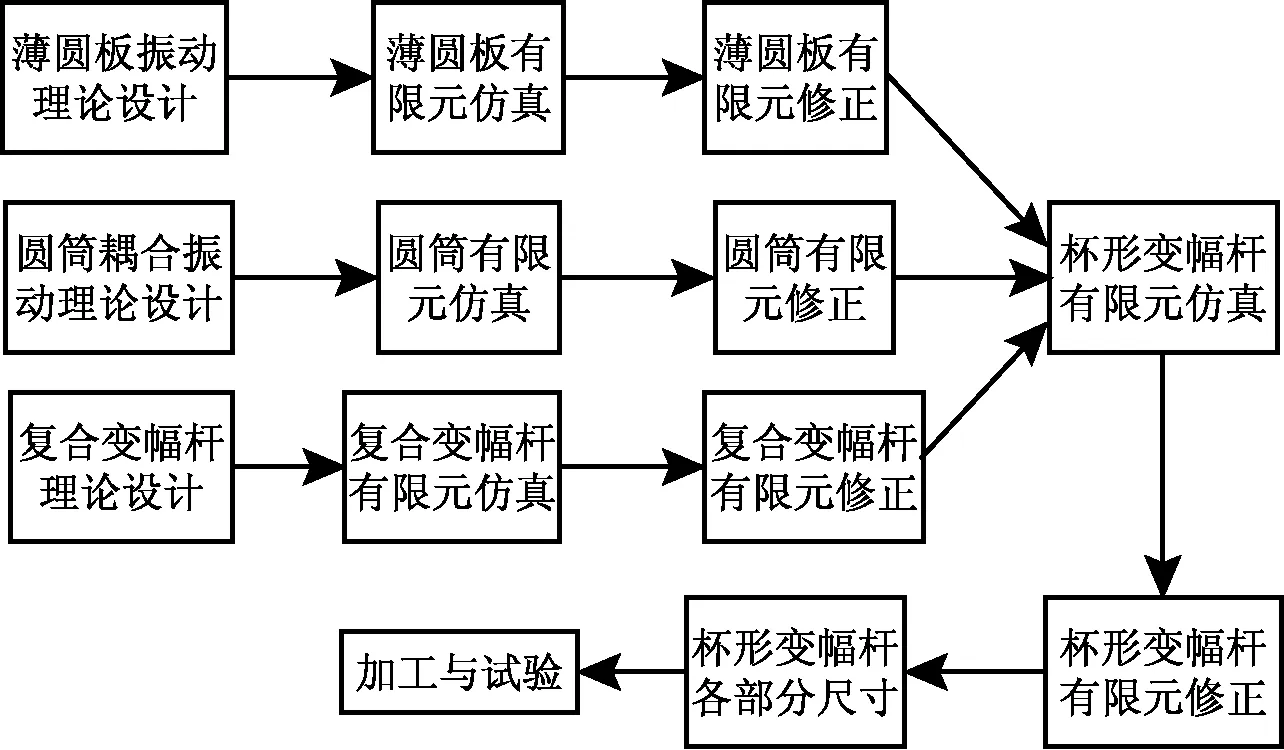
图3 杯形工具复合变幅杆设计流程图

2.1 薄圆盘尺寸确定

对式(4)求解后得kna值，根据设计要求取第二阶kna=5.454 7；设定薄圆盘厚e=10 mm，经式(5)得薄圆盘在该频率下产生二阶弯曲振动时的半径R(R=a/2)，R=55 mm，对所求的薄圆板进行有限元仿真。

提取模态结果后发现：薄圆盘弯曲振动的谐振频率为21 605 Hz，如图4(a)。通过减小薄圆盘半径以增大频率，使其与目标频率趋于一致，修正后薄圆盘半径R=50.2 mm，弯曲振动谐振频率为25 022 Hz，模态分析结果，如图4(b)所示。

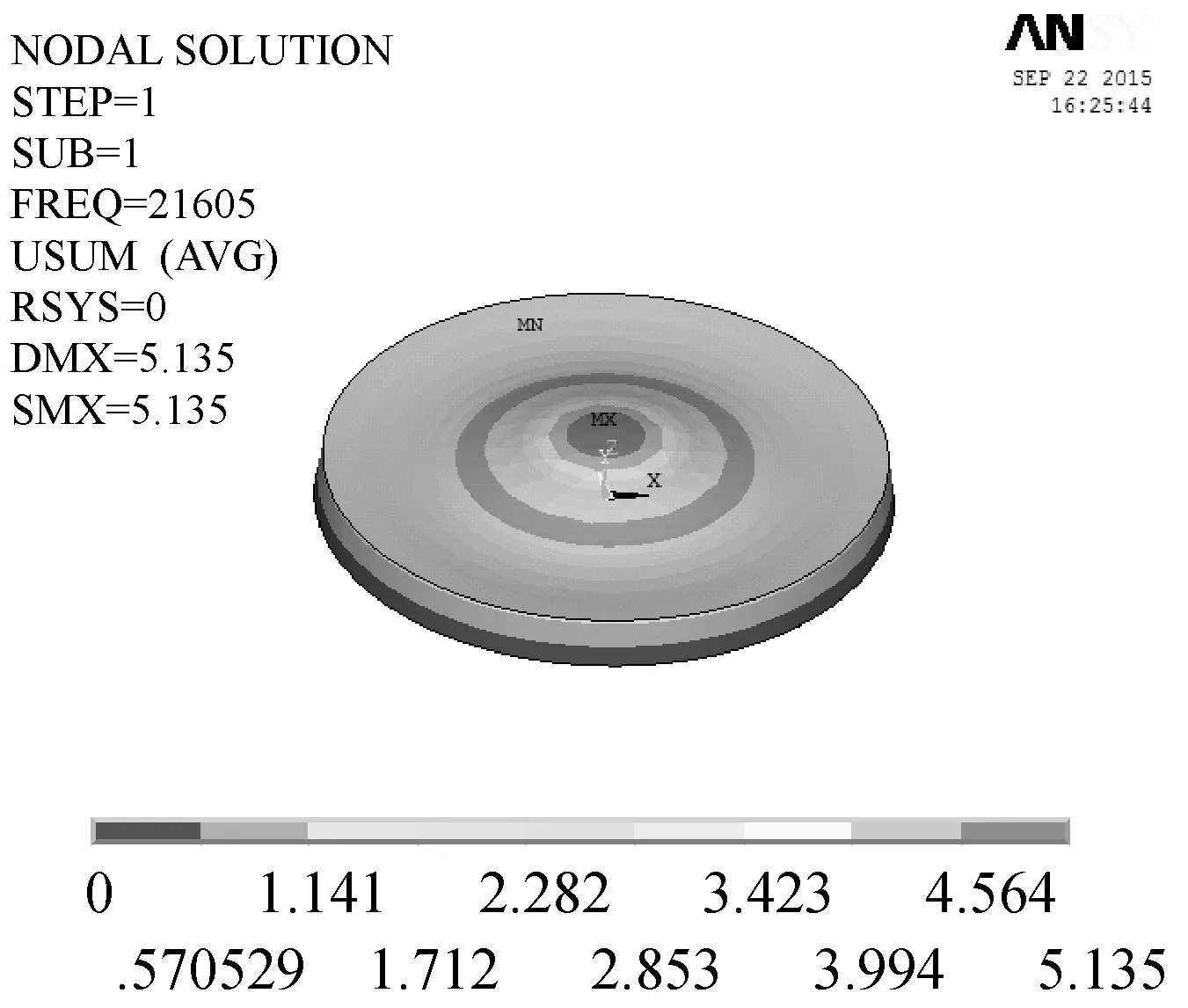
(a) 修正前薄圆盘谐振位移图

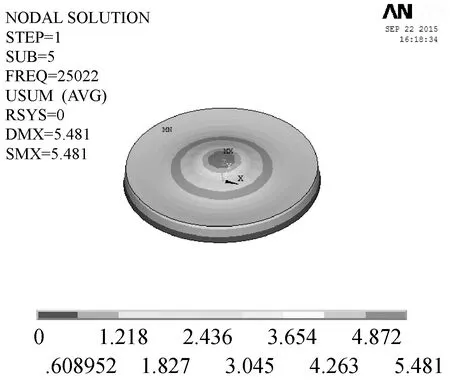
(b) 修正后薄圆盘谐振位移图

2.2 杯形工具尺寸确定

为保证杯形头刚度，设定壁高h=24 mm，根据式(6)和式(7)，即可求得圆筒的纵向频率为22 930 Hz，与设计频率相差很大。但是为保证杯形头工作过程中的径向刚度，不再修正圆筒高，通过修正圆盘半径使其与目标频率一致，当R=44.5 mm时，圆筒与圆盘耦合的杯形头谐振频率为24 956 Hz，如图5所示。

图5 杯形头谐振位移

2.3 圆柱圆锥变幅杆的尺寸确定

由于振动系统工作频率为25 kHz，因此换能器输出端尺寸已定，为减少振动系统能量损耗，要求换能器输出端直径与变幅杆输入端相等，即D1=45 mm；为提高杯形工具头的振动效果，需增大变幅杆输出与杯形工具头的接触面积，选取D2=28 mm。此外，设定L1=58 mm，运用MATLAB计算复合变幅杆频率方程(8)，最终确定圆锥段L2长为55 mm。对所求的变幅杆进行有限元仿真，其纵向谐振频率为25 061 Hz，如图6所示。变幅杆的仿真频率与理论计算基本一致，无需进一步修正。

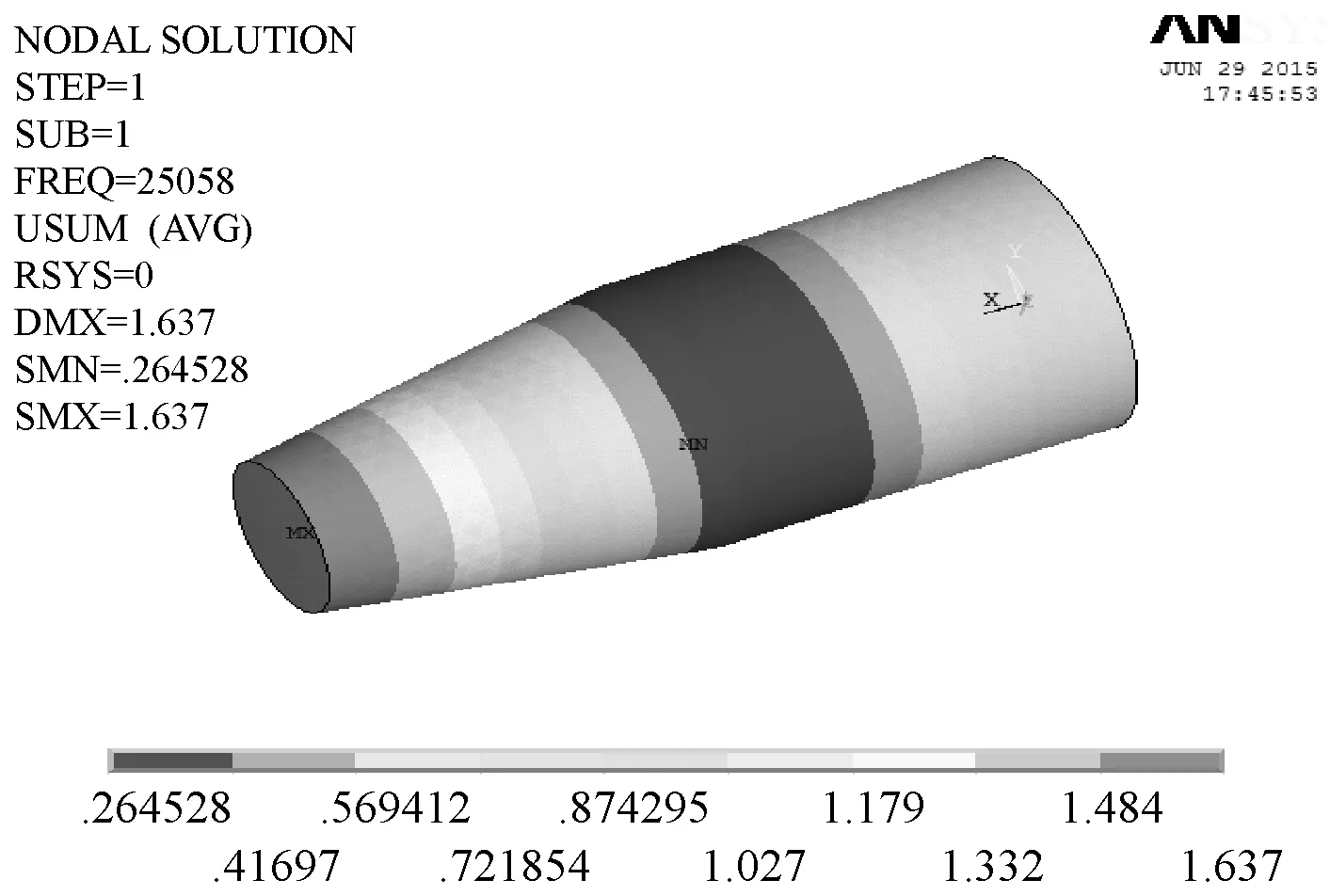
图6 复合变幅杆谐振位移

2.4 杯形工具复合变幅杆的尺寸确定

将杯形头与圆柱圆锥变幅杆耦合到一起进行有限元分析，其中圆柱圆锥变幅杆赋予45#钢性能参数，杯形工具赋予6070硬铝性能参数，具体模态分析结果如图7。

(a) 修正前系统谐振位移

(b) 修正后系统谐振位移

由图7可知，杯形头与变幅杆耦合后谐振频率为25 316 Hz，与设计频率相差300 Hz，需进一步修正。通过减小杯形头的底厚以调节系统的谐振频率，修正后杯形工具复合变幅杆谐振频率为25 044 Hz，满足设计要求。此外，可通过有限元软件后处理功能对杯形工具复合变幅杆进行路径定义、路径映射，提取相对位移结果后发现在一定的输入载荷下，杯形头外圆末端的相对径向振幅为1.449 m，相对纵向振幅为0.457 m，从而得出杯形头径向振动相对位移为纵向的3倍，如图8～图9所示。最终确定杯形工具复合变幅杆各部分尺寸，具体参数，如表2所示。

图8 杯形头纵向相对位移随壁高变化

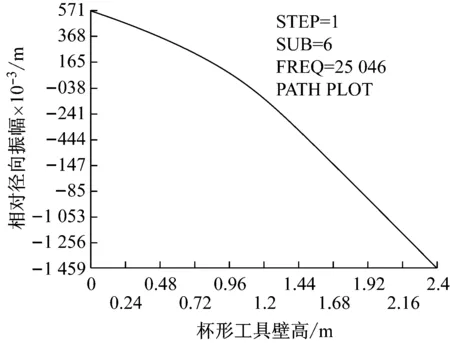
图9 杯形头径向相对位移随壁高的变化

表2 杯形工具复合变幅杆各部分尺寸参数

Tab.2 The size of the cup horn parameters mm

大端直径D1小端直径D2圆柱端L1圆锥段L2壁厚h底厚e内径b外径a452858552497189

3 变幅杆振动试验

3.1 阻抗特性试验研究

采用北京邦联时代电子科技有线公司的PV70A阻抗分析仪对所设计杯形工具复合变幅杆进行阻抗分析。由图10可知，变幅杆实测谐振频率在25 kHz附近，与ANSYS模态分析结果基本吻合，且导纳圆圆度较好，电导曲线正常。振动系统的机械品质因数较高，即系统的电声转化效率高，说明所设计变幅杆的尺寸及其结构都十分合理。

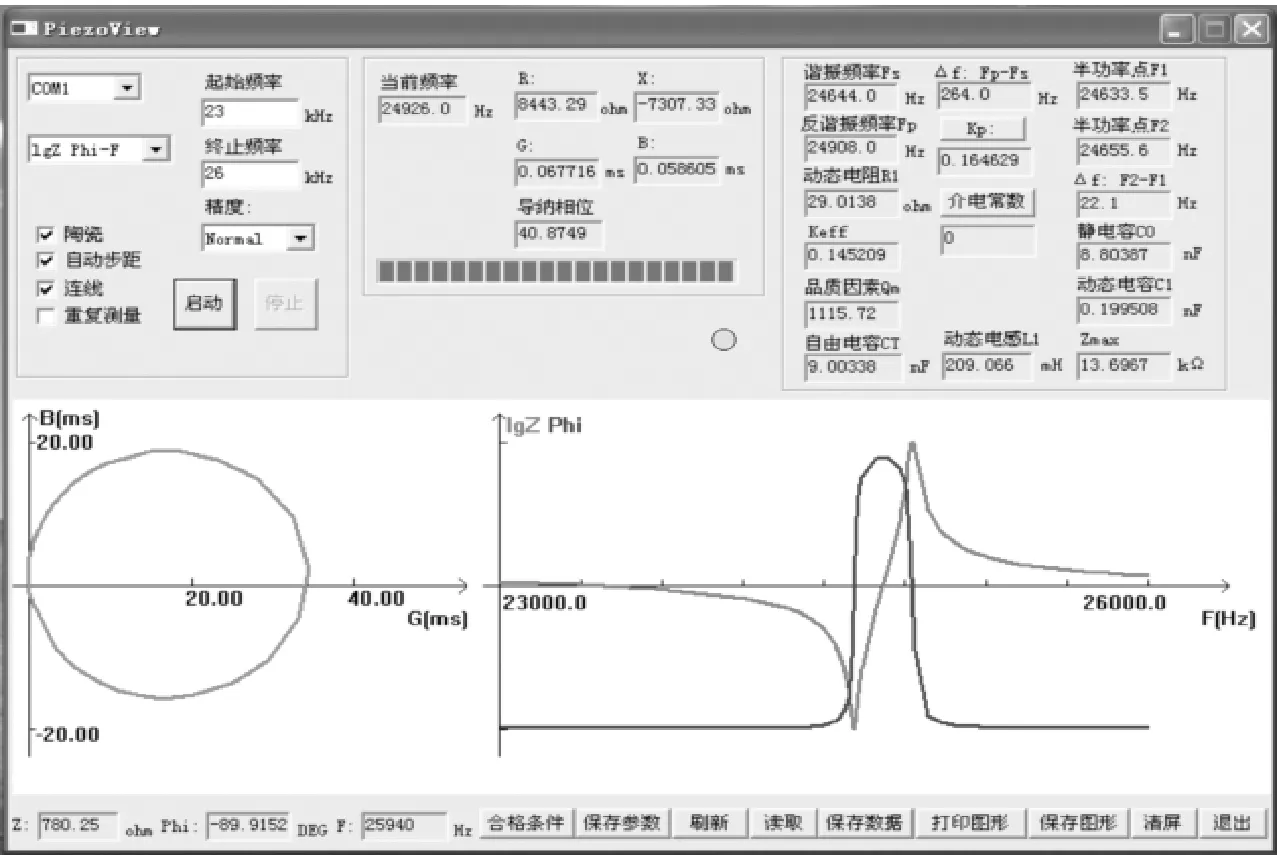
(b) 超声振子阻抗分析测试结果

3.2 振幅特性试验研究

采用高精度的KEYENCE-700K激光位移传感器对系统振幅展开测试。由于杯形工具复合变幅杆输出端振动形式表现为纵径耦合，因此应在杯形头端面和周向分别测试纵向和径向振幅，如图11所示。

(a) 径向测试振幅

(b) 轴向测试振幅

由图12可知，杯形工具复合变幅杆纵向振幅为2.7 μm，径向振幅为7.5 μm。由于杯形工具复合变幅杆的输出端是杯形头，其壁高较小，纵径耦合过程以径向振动为主，因此径向振幅大于纵向振幅，同时这也与有限元分析所得径向振幅是纵振3倍的仿真结果基本一致。

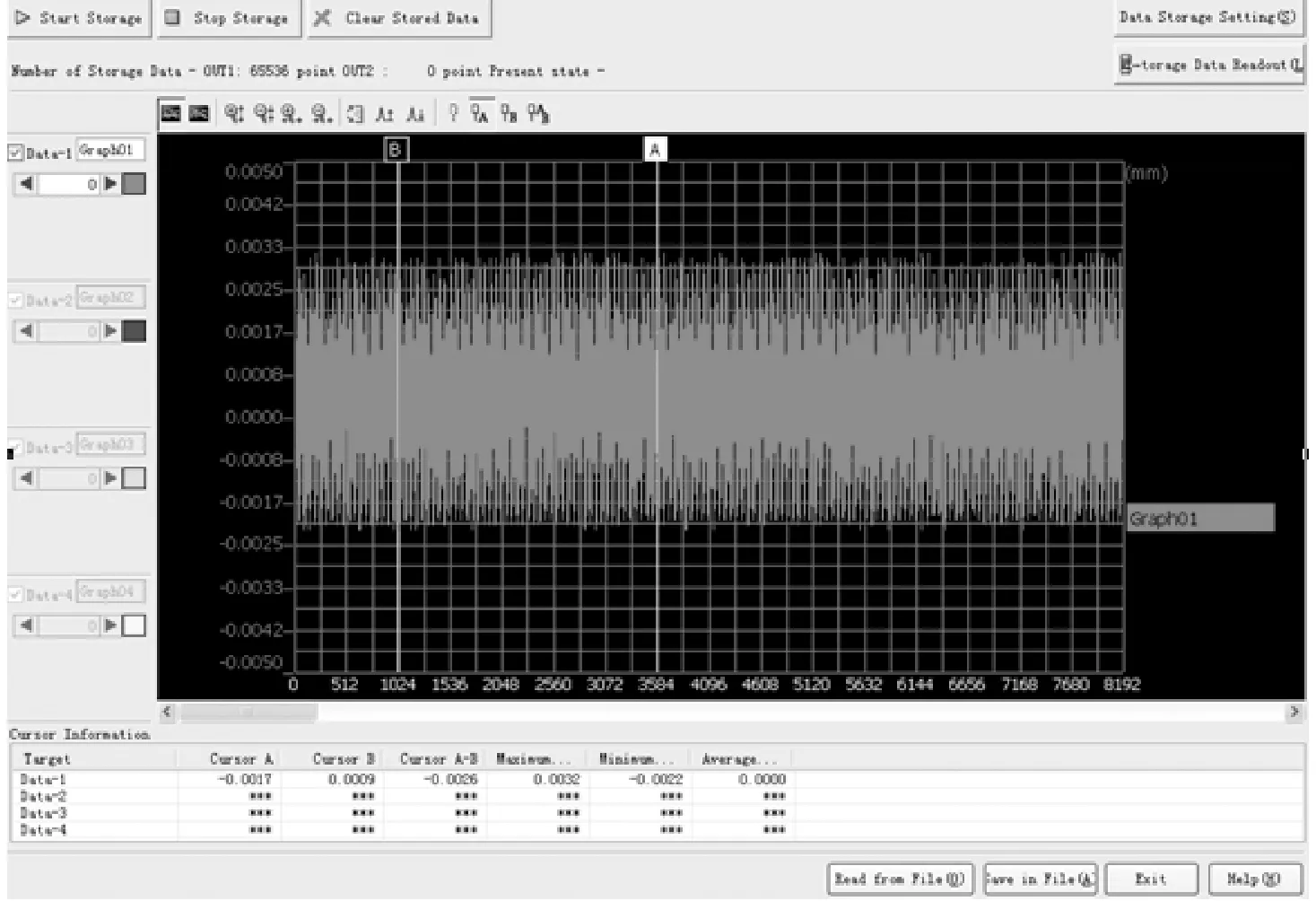
(a) 纵向振动振幅图

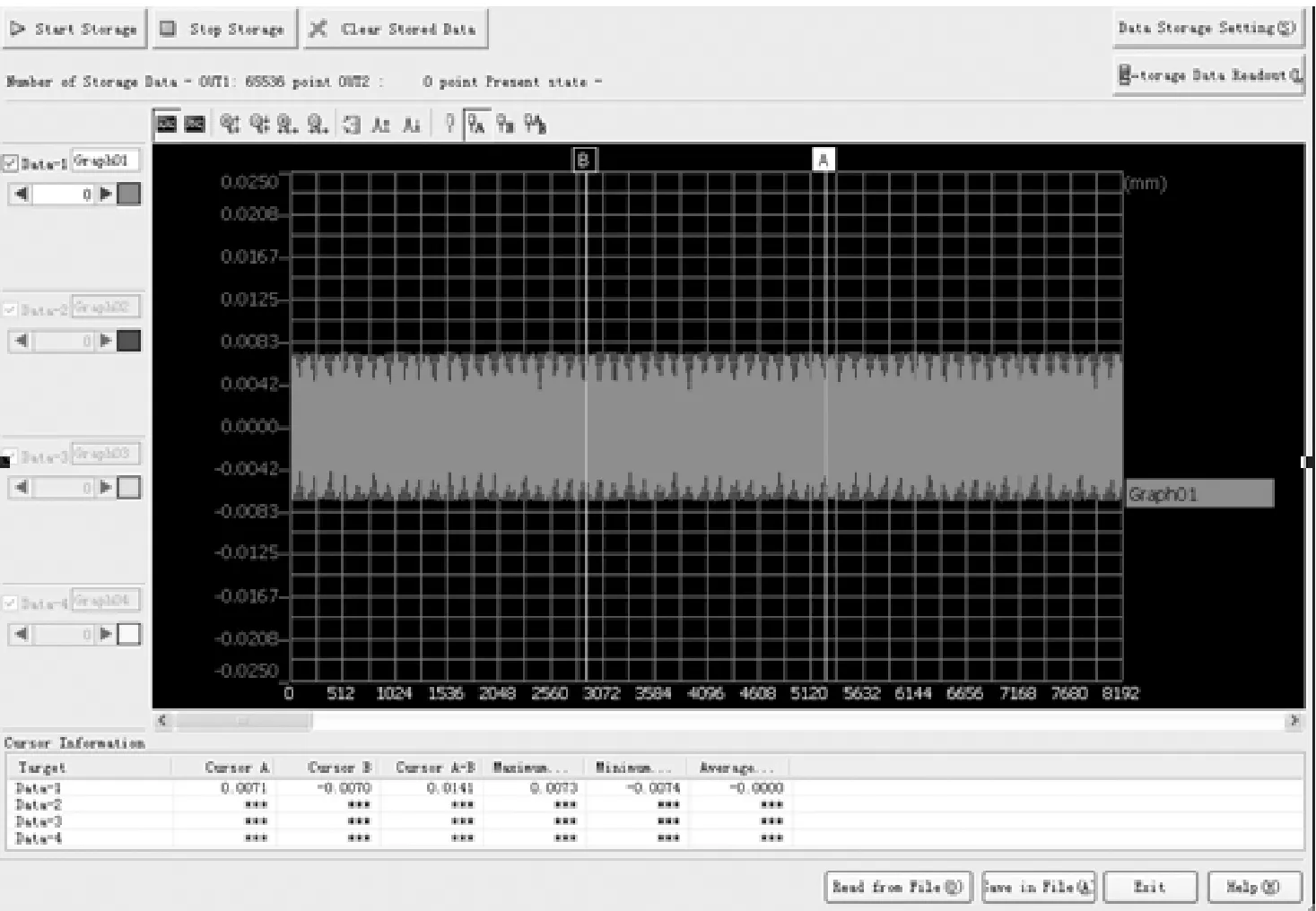
(b) 径向振动振幅图

为了进一步研究杯形工具复合变幅杆是否处于谐振状态，在杯形头纵向端部、壁高方向分别有规律地设定八个测试点，如图13所示。具体测试结果，如图14所示。

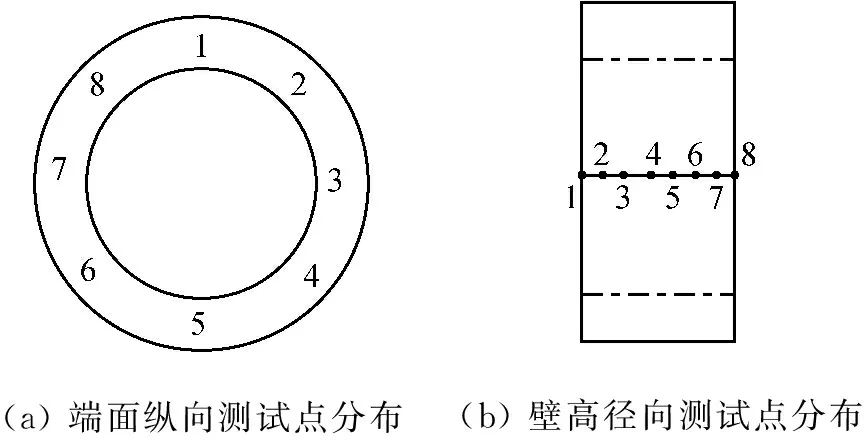
(a)端面纵向测试点分布(b)壁高径向测试点分布

图13 测试点分布

Fig.13 Test point distribution

由图14(a)可知，杯形头端面八个测试点的输出振幅基本上不变，均在2.7 μm左右浮动。由图14(b)可知，杯形头径向振幅随着壁高的增大而增大。因此，杯形工具复合变幅杆工作时处于谐振状态。

4 杯形头几何参数对振动系统的影响研究

杯形头为大尺寸构件，会对系统谐振产生较大影响，因此有必要对杯形头展开分析。本文通过仿真与试验相结合的形式，从杯形头壁高、底厚、内径三个角度来探求杯形头几何形状参数对杯形工具复合变幅杆谐振频率的影响规律，其中杯形头初始尺寸为外径a为89 mm，内径b为71 mm，底厚e为9 mm，壁高h为24 mm，4种不同尺寸的杯形头，如图15所示。

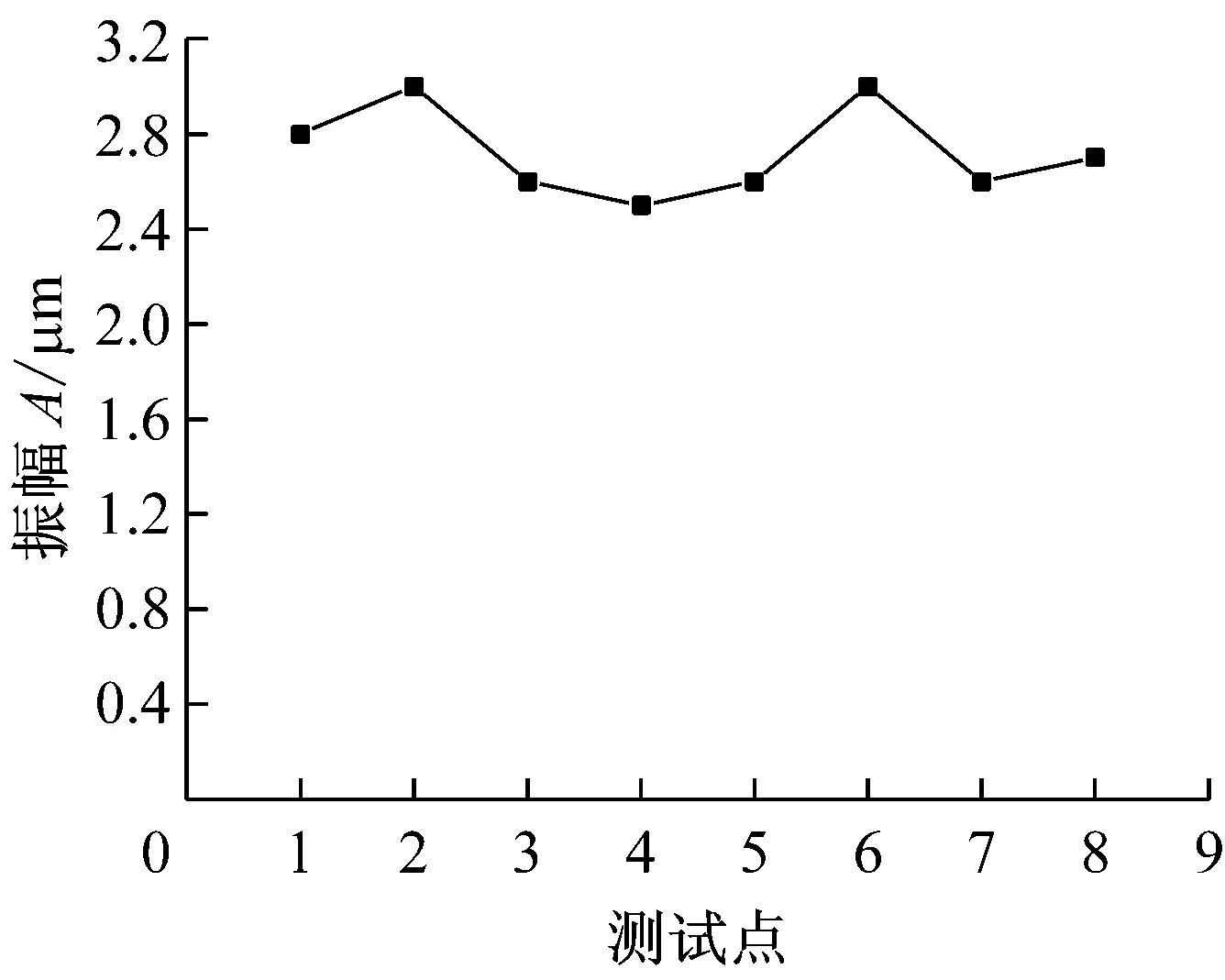
(a) 端面纵向振幅

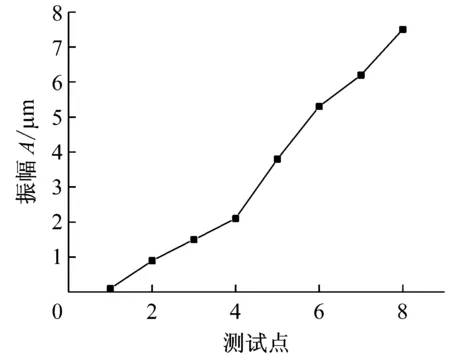
(b) 壁高径向振幅

图15 4种不同尺寸的杯形头

4.1 杯形头壁高h对杯形工具复合变幅杆谐振频率的影响

由图16可知，在杯形头底厚、内径不变的情况下，杯形头壁高由21 mm增大到24 mm的过程中，杯形工具复合变幅杆谐振频率的仿真与试验值都逐渐降低且变化趋势一致，虽然仿真值略大于试验值，但误差均在5%以内，仿真结果仍具有一定参考价值。

4.2 杯形头底厚e对振动系统频率的影响

由图17可知，在壁高、内径不变的条件下，杯形工具复合变幅杆谐振频率随着底厚的减小而降低，并且仿真与试验结果基本吻合。随着底厚的减小，测试值与仿真值越来越接近，主要由于底厚的减小致使杯形头与变幅杆装配间隙变小，结构更紧凑。

图16 壁高与谐振频率的关系

图17 底厚与谐振频率的关系

4.3 杯形头内径b对振动系统频率的影响

由图18可知，仿真与测试结果具有相同的变化规律，即在底厚、壁高不变的条件下，杯形工具复合变幅杆的谐振频率随着内径的增大而降低，内径每增大1 mm，其谐振频率减小200～300 Hz不等。

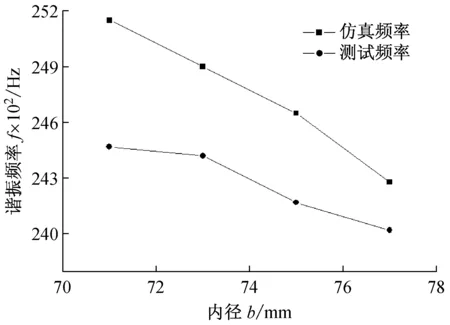
图18 内径与谐振频率的关系

通过对上述分析发现试验检测频率与仿真频率存在误差，产生这种结果的原因如下：① 杯形头与变幅杆采用的是螺纹连接，接触不够紧密，造成能量损失；② 杯形头和圆柱圆锥变幅杆不是同一种材料，波在不同材料中传播时产生了大量反射；③ 杯形头与变幅杆装配时预留2 mm左右的空隙，与仿真假设不同；④ 有限元分析时网格单元体的大小及密度对变幅杆谐振频率影响非常大，由于计算机的计算能力有限，变幅杆划分单元数量不足，难免比实际频率要大。

5 结 论

(1) 鉴于超声磨削技术在硬脆材料曲面高精度加工方面所具备的独特优势，基于弯曲振动理论、耦合振动理论和变幅杆设计理论，结合有限元分析法，设计了工作频率为25 kHz的超声杯形工具复合变幅杆。

(2) 对所设计的杯形工具复合变幅杆进行阻抗分析和振幅特性试验，结果显示：振动系统频带宽、动态电阻小、声电转换效率高，说明变幅杆结构设计合理；杯形头表现为以径向振动为主的纵径耦合振动形式，且输出端面纵向振幅变化不大，沿杯形头轴向越靠近输出端面其径向输出振幅越大，表明系统处于谐振状态。

(3) 利用有限元仿真分析和试验测试的方法，研究了杯形头几何参数对振动系统谐振频率的影响：当减小杯形头的壁高、内径时，变幅杆的实测与仿真频率都随之升高；当减小其底厚时，变幅杆实测与仿真频率都随之降低，且实测与仿真分析值高度吻合。

[1] 周志雄,周秦源,任莹晖.复杂曲面加工技术的研究现状与发展趋势[J].机械工程学报,2010,46(17):105-113.

ZHOU Zhixiong, ZHOU Qinyuan, REN Yinghui.Current research and development trends of complex surface machining technology[J].Journal of Mechanical Engineering, 2010, 46(17):105-113.

[2] 任力强.大口径光学曲面精密加工系统研制[D].北京:北京理工大学,2008.

[3] 曹凤国.超声加工[M].北京:化学工业出版社,2014.

[4] 赵升吨,李泳峄,范淑琴.超声振动塑性加工技术的现状分[J].中国机械工程,2013,24(6):835-840.

ZHAO Shengdun, LI Yongyi, FAN Shuqin. Status analysis of plastic processing technologry with ultrasonic vibration[J].China Mechanical Engineering, 2013, 24(6):835-840.

[5] LIM F C N, CARTMCLL M P, CARDONIA, et al. A preliminary investigation into optimizing the response of vibrating systems used for ultrasonic cutting[J]. Journal of Sound and Vibration, 2004(272):1047-1069.

[6] YA G, QIN H W, YANG S C, et al. Analysis of the rotary ultrasonic machining mechanism[J]. Journal of Material Processing Technology, 2002，129(1/2/3):182-185.

[7] MOHAMMAD M A Z, MOHAMMAD R R, AMIR A. Investigation of the effect of cutting speed and vibration amplitude on cutting forces in ultrasonic-assisted milling[J]. Journal of Engineering Manufacture, 2012, 226(7):1185-1191.

[8] 许龙,林书玉. 模式转换型超声塑焊振动系统的设计[J]. 声学学报,2010,35(6):683-693.

XU Long,LIN Shuyu. Design of ultrasonic vibration system with vibration mode-conversion for ultrasonic plastics welding[J]. Acta Acustica，2010,35(6)：683-693.

[9] 皮钧,纪跃波. 纵波回形变幅杆的研究[J]. 振动、测试与诊断，2010,30(1):65-69.

PI Jun,JI Yuebo. Study on longitudinal vibration of a folded acoustic horn[J].Journal of Vibration,Measurement &Diagnosis, 2010,30(1):65-69.

[10] 徐芝纶.弹性力学(下册)[M]. 北京: 人民教育出版社，1982.

[11] 张小丽,林书玉,付志强,等.弯曲振动薄圆盘的共振频率和等效电路参数研究[J].物理学报,2013,62(3):1-6.

ZHANG Xiaoli，LIN Shuyu，FU Zhiqiang, et al. Study on resonance frequency and equivalent circuit parameters of a thin disk in flexural vibration[J].Acta Physical Sinica,2013,62(3):1-6.

[12] 马奶连，贺西平.弯曲振动薄圆盘的最佳尺寸设计[J].云南大学学报(自然科学版)，2014,36(3):366-370.

MA Nailian, HE Xiping. The best dimension design of flexural vibration thin circular plate[J]. Journal of Yunnan University(Natural Science), 2014, 36(3): 366-370.

[13] LIN Shuyu.Coupled vibration of isotropic metal hollow cylinders with large geometrical dimensions[J]. Journal of Sound and Vibration, 2007,305(1):308-316.

Design of a cup horn and its vibration characteristics analysis

CHEN Huizi1, ZHAO Bo1, ZHAO Jinzhui1,2, GAO Guofu1

(1.School of Mechanical and Power Engineering, Henan Polytechnic University, Jiaozuo 454000，China;2.Zhengzhou Research Institute for Abrasives & Grinding Co.,Ltd., Zhengzhou 450007， China)

Aiming at problems of poor machining precision, low efficiency, and high processing cost in curve surface processing of hard and brittle materials, a kind of ultrasonic cup horn suitable for high precision machining of curve surfaces of hard and brittle materials was designed by combining the theoretical analysis and the finite element method. Afterwards,the impedance characteristic analysis and the vibration performance tests of the designed cup horn were performed. The results showed that the structure of the horn is reasonable and its vibration effect is good. Finally, through the finite element calculation and tests comparative analysis, the influences of wall height, bottom thickness, and inner diameter of the cup shaped head on the cup horn resonant frequencies were studied. The results showed that the resonance frequencies of the horn increase with increase in bottom thickness and decrease with increase in wall height, and inner diameter of the cup shaped head; the test results and the simulation analysis ones agree well each other.

brittle materials; curve surface processing; cup horn; finite element analysis; resonant frequency

国家“863”计划资助项目(2013AA040103)

2015-08-11 修改稿收到日期：2015-10-09

陈汇资 男，硕士生，1989年生

赵波 男，教授，博士生导师，1956年生

TB559

A

10.13465/j.cnki.jvs.2017.09.024