饱和多孔介质不同动力耦合形式数值分析

刘 宝， 苏 谦,2， 刘 亭， 李 婷

(1. 西南交通大学 土木工程学院， 成都 610031；2. 西南交通大学 高速铁路线路工程教育部重点实验室， 成都 610031)

饱和多孔介质不同动力耦合形式数值分析

刘 宝1， 苏 谦1,2， 刘 亭1， 李 婷1

(1. 西南交通大学 土木工程学院， 成都 610031；2. 西南交通大学 高速铁路线路工程教育部重点实验室， 成都 610031)

Biot饱和多孔介质波动行为的数值模拟在众多工程领域中具有重要的意义和作用，由于固相与液相耦合方程难以解耦，使该问题的数值模拟难度较大。针对饱和多孔介质中部分耦合u-p及全耦合u-p-U方程形式的特征，推导了相应动力耦合控制方程的有限元弱形式，并引入不同耦合形式的饱和多孔介质时域黏性边界，综合利用Comsol Multiphysics提供的偏微分方程应用模式进行二次开发求解，通过一维饱和多孔介质动力响应的解析解和数值解验证了模型求解技术的合理性和可行性，基于u-p-U耦合形式探讨了冲击荷载作用下干砂饱和砂地基动力固结中应力波传播特性。计算结果表明慢纵波对动力固结的影响比较显著，合理的冲击荷载持续时间有利于固结效果的改善。

饱和多孔介质；Biot模型；Comsol Multiphysics；u-p方程；u-p-U方程

饱和多孔介质的波动问题涉及诸多工程领域，特别在岩土工程、海洋工程、水利水电工程等领域中普遍存在。目前，研究饱和多孔介质宏观动力行为的理论主要有：Biot波动理论[1-2]和多孔介质理论[3]，两种理论在工程中已被广泛应用，比较而言，Biot波动理论在不同工程领域中得到了更为广泛和深入的应用。自Biot饱和多孔介质波动理论建立以来，国内外学者采用解析或数值手段对Biot波动方程及其工程应用进行了广泛的研究。

饱和多孔介质动力方程常用的解析方法多采用积分变换、级数展开和势函数分解等手段将其偏微分控制方程转化为变换域中的常微分方程，再通过逆变换获得空间域-时域中的解[4-5]，在一维等简单情形下可通过逆变换以获得其解析表达式[6-7]，对于大多数的研究问题尚需数值积分实现逆变换。时刚等[8]运用了薄层法对层状饱和地基动力响应进行求解，避免了逆变换过程中的数值积分，在一定程度上提高了计算效率和计算精度。

饱和多孔介质波动方程数值求解常用的方法包括有限元法、有限差分法及边界元法等[9]，有限元方法由于能够适应任意复杂几何形体、边界条件以及不同的材料模型而被广泛采用。Schanz[10]对Biot波动方程的有限元数值分析做了较为深入的研究，根据不同的简化假设，按不同的基本未知量提出了u-p、u-U、u-p-U耦合形式的有限元控制方程，并指出在渗透系数和荷载频率较小的情况，可以将流体相对于土骨架运动的惯性力忽略不计即u-p简化形式，但并未明确的给出可忽略流体惯性项的量化条件。既有研究中基于u-p简化形式采用有限元隐式算法进行饱和多孔介质波动问题的研究比较多见[11-12]。Zhao等[13]根据u-U形式采用显式有限元解法研究了二维饱和地基表面刚性基础的振动问题，显式有限元法避免了整体刚度矩阵的组装，从而提高了计算效率。但u-U形式在固相与液相两者压缩性差距较大时易出现体积锁死问题，而u-p-U形式通过引入压力场克服了该问题，另外，文献[14]基于u-p-U控制方程开发了相应的有限元程序，研究了砂土液化的问题，并开展了相关的室内试验进行了对比验证[15]，比较而言，目前有关u-p-U形式的文献研究报道较少。

综上可以看出，饱和多孔介质不同动力耦合形式的有限元求解多通过自行编制有限元程序实现，但有限元程序的编写涉及饱和多孔介质动力单元的开发、求解算法及合理人工边界的实施等关键问题，具有一定的理论深度和难度。当前广泛应用的功能强大的商业有限元软件Ansys、Abaqus和Comsol Multiphysics等均未提供饱和多孔介质不同耦合形式的动力单元，可通过其提供的开放接口编写内嵌语言或子程序实现，而目前这方面的研究报道尚不多见。

鉴于Comsol Multiphysics在定义和耦合偏微分方程灵活方便的优势，本文通过积分变换得到饱和多孔介质动力控制方程u-p及u-p-U的弱形式，引入Akiyoshi[16]给出的不同耦合形式的饱和多孔介质时域黏性边界，综合利用该软件提供的偏微分方程应用模式进行求解，通过一维饱和多孔介质动力响应的解析解验证了不同耦合形式模型的正确性，在此基础上，基于u-p-U耦合形式建立干砂-饱和砂地基耦合模型，并利用该模型着重分析冲击荷载下该体系的应力波传播特性，为研究饱和多孔介质动力响应问题提供了一种方便快捷的计算模式。根据该计算模式，可灵活地对研究中新提出的应力场控制方程、渗流场控制方程及固液相耦合关系发生变化的饱和多孔介质波动方程实现计算分析，以满足实际问题的需要。

1 饱和多孔介质动力控制方程

1.1 全耦合u-p-U方程

采用文献[17]给出的基本方程，考虑土颗粒的压缩性

土骨架本构方程

(1)

整体平衡方程

(2)

流体平衡方程

(3)

渗流连续方程

(4)

将式(3)代入式(4)中得

(5)

其中流体位移未知量Ui=ui+wi/n，式(2)、式(5)与式(1)构成了饱和多孔介质u-p-U动力耦合形式的方程。

在式(1)中：εij为固相骨架应变；λs、μs为固相骨架Lame常数；p为孔隙水压；α为Biot常数，α=1-Kb/Ks，Kb,Ks分别为固相骨架、颗粒的体积模量，Kb=λs+2μs/3；δij为Kronecker符号。在式(2)中：ρm=nρf+(1-n)ρs为总体有效密度；ρs和ρf分别为固相骨架密度和流体密度；n为孔隙率；u为固相骨架位移。在式(3)中：wi为流体相对于固相骨架的位移，在实际应用中根据；kf为动力渗透系数。在式(4)中，Q为流体的压缩系数，Q=(α-n)/Ks+n/Kf，Kf为流体体积模量。

1.2 部分耦合u-p方程

Zienkiewicz等通过略去Biot方程中的孔隙流体相对加速度项，推导出以土骨架位移u和孔压p为变量的简化控制方程。

平衡方程

(6)

达西运动方程

(7)

渗流连续方程

(8)

将式(7)代入式(8)中得

(9)

式(6)、式(9)与式(1)构成了饱和多孔介质u-p动力耦合形式的方程。

2 有限元模型的建立

2.1u-p方程的有限元弱形式

Comsol Multiphysics采用虚位移原理对偏微分方程表达的问题进行描述，因此需根据虚位移原理推导耦合场控制方程的等效弱形式。在式(2)与式(5)中分别乘以虚变量δu和δp，然后在求解区域范围内对方程进行积分，为使积分方程能够引入边界条件，应用Green-Gauss公式对积分方程进行分部积分，从而可得到耦合方程的弱形式。式(2)的积分形式为

(10)

由Green-Gauss公式得

(11)

式(5)的积分形式为

(12)

同理由Green-Gauss公式得

▽Tp(kij▽p)dΩ-

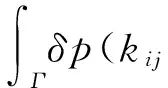
(13)

利用Galerkin加权余量法离散得到以土骨架位移u和孔压p为变量的u-p形式控制方程

u(x,t)=NuU(t);p(x,t)=NpP(t)

(14)

δu(x,t)=Nu;δp(x,t)=Np

(15)

式中，Nu，Np分别为U(t)，P(t)的插值形函数，以土骨架位移u和孔压p表达的u-p形式的有限元控制方程为

(16)

(17)

其中，

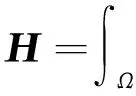
2.2u-p-U方程的有限元弱形式

采用相同的方式可得出u-p-U方程的有限元弱形式

(18)

其中，

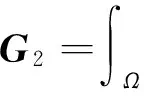
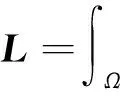
2.3 黏性人工边界

饱和多孔介质中由于固相和液相间存在相互作用，包含两类压缩波和一类剪切波，边界的处理问题变得较为复杂[18]，饱和多孔介质的人工边界， 除了要处理位移边界条件外， 还要考虑孔压在人工边界的传播。目前针对饱和多孔介质的人工边界的建立和研究已取得诸多成果，用的比较多的是透射边界、 黏性边界和在黏性边界基础上发展的黏弹性边界[19]。本文采用Akiyoshi饱和多孔介质黏性边界，通过设置阻尼器来吸收传到边界上的波动能量，从而消除或减小在边界上的反射。

(1)u-p耦合形式

法向应力

(19)

切向应力

(20)

边界压力

(21)

(2)u-p-U耦合形式

法向应力

(22)

切向应力

(23)

边界压力

(24)

Vp为压缩波在饱和多孔介质中的传播速度

(25)

Vs为剪切波在饱和多孔介质中的传播速度

(26)

2.4 模型建立的实施

Comsol是一款基于求解偏微分方程组的多场耦合计算平台，具有较强的计算性能及多场直接耦合的能力，其中PDE模块可以灵活地建立数学模型并基于该方程对问题进行求解，现将模型建立的关键流程进行描述：① 在模型向导中创建几何模型维度，通过MathematicsPDE Interfaces添加Weak Form PDE物理场，并将u-p或u-p-U动力耦合方程中对应的待求变量输入，选择Time Dependent后进入主图形界面；② 在模型树中，按照u-p或u-p-U中应力场、渗流场控制方程形式定义表达式，根据软件约定的弱形式书写规范将定义的方程表达式在”Weak Expressions”栏中输入；③ 建立几何模型并添加相应的人工边界，位移边界可通过PDE模式中内置的Dirichlet Boundary Condition(狄式边界)添加，应力边界通过添加Weak Contribution来实现；④ 模型网格划分与求解，网格单元默认为拉格朗日二次单元，网格的大小及时间步长选取应满足CFL稳定性原则，模型求解由内置的直接求解器或迭代求解器自动完成，即可实现饱和多孔介质动力耦合有限元模型的建立。

3 模型的验证及应用

Boer等给出了一维不可压缩饱和多孔介质动力响应的解析解，本文利用此解析解进行对比验证，算例的计算模型，如图1所示，模型的横向尺寸取1 m，竖向尺寸取4 m，按照上文中模型实施流程进行建模，边界条件分两种工况进行设置；第一类工况为底边为固定且不透水边界，左右边界水平位移固定且不发生渗流，上表面为自由透水边界，即孔压为0；第二类工况为底部为黏性吸收边界，其余边界条件同上，位移边界通过内置的狄式边界添加，应力边界通过在Weak Contribution栏输入对应的表达式实现。采用四边形拉格朗日二次单元划分网格，每个节点包含3个自由度。材料参数取值，如表1所示，土柱承受的动力荷载的时程曲线为函数f(t)，如图1所示。计算时间步长取0.001 s，荷载持续时间为0.3 s。本研究中由于求解问题的规模不太大，选用精度高、稳定性好、高效的稀疏直接求解器MUMPS进行求解，时间积分方法采用general-α方法，该方法具有无条件稳定、二阶精度的优点，并且能够通过控制数值阻尼，有效滤除高频数值频散响应[20]。

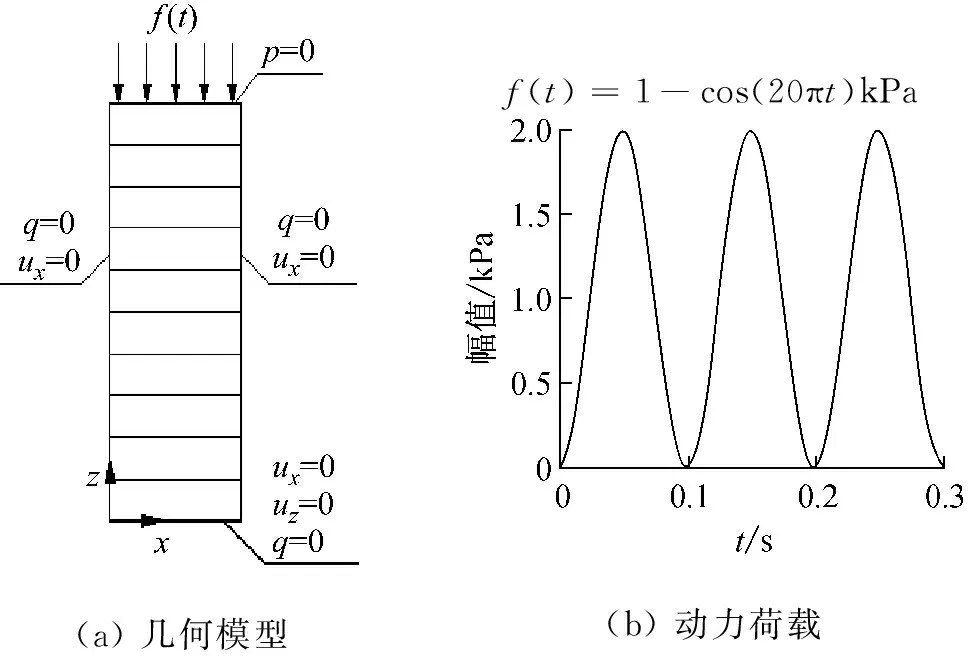
(a)几何模型f(t)=1-cos(20πt)kPa(b)动力荷载

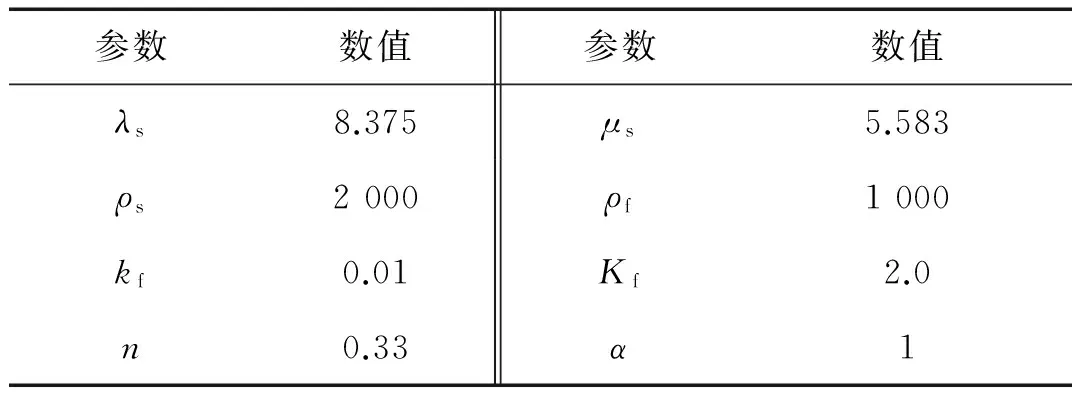
表1 文献[6]材料参数

3.1u-p及u-p-U模型的验证

在u-p耦合模型中，基本未知量为固相位移和孔隙水压，图2表示数值解与已知解析解的对比结果图，由图中可知，采用固定边界时，开始阶段的数值结果与解析解结果几乎一致，随着时间的推移，应力波传播到底部时，在固定边界产生反射波，进而使应力波在上部和下部边界产生多次反射，造成计算结果的偏差越来越大。采用Akiyoshi黏性吸收边界时，数值计算结果与解析解的结果非常吻合，可以看出，黏性边界比固定边界的计算结果更加合理。

在u-p-U耦合模型中，基本未知量为固相位移、孔隙水压及液相位移，能够考虑液相对于固相相对加速度的影响。由图3可知，采用黏性边界能够减少应力波在底部边界的反射，从而使数值计算与解析解结果相符合，而采用固定边界时，由于底部产生的反射波的影响，使得数值结果与解析解结果随着时间的推移偏差越来越明显。由图3(a)、图3(b)可知，土柱在动荷载作用下固相位移与液相位移的运动方向相反，固相向下运动，液相向上运动从而不断地挤出孔隙，反映出饱和多孔介质中固相与液相由内摩擦引起的黏弹性质。

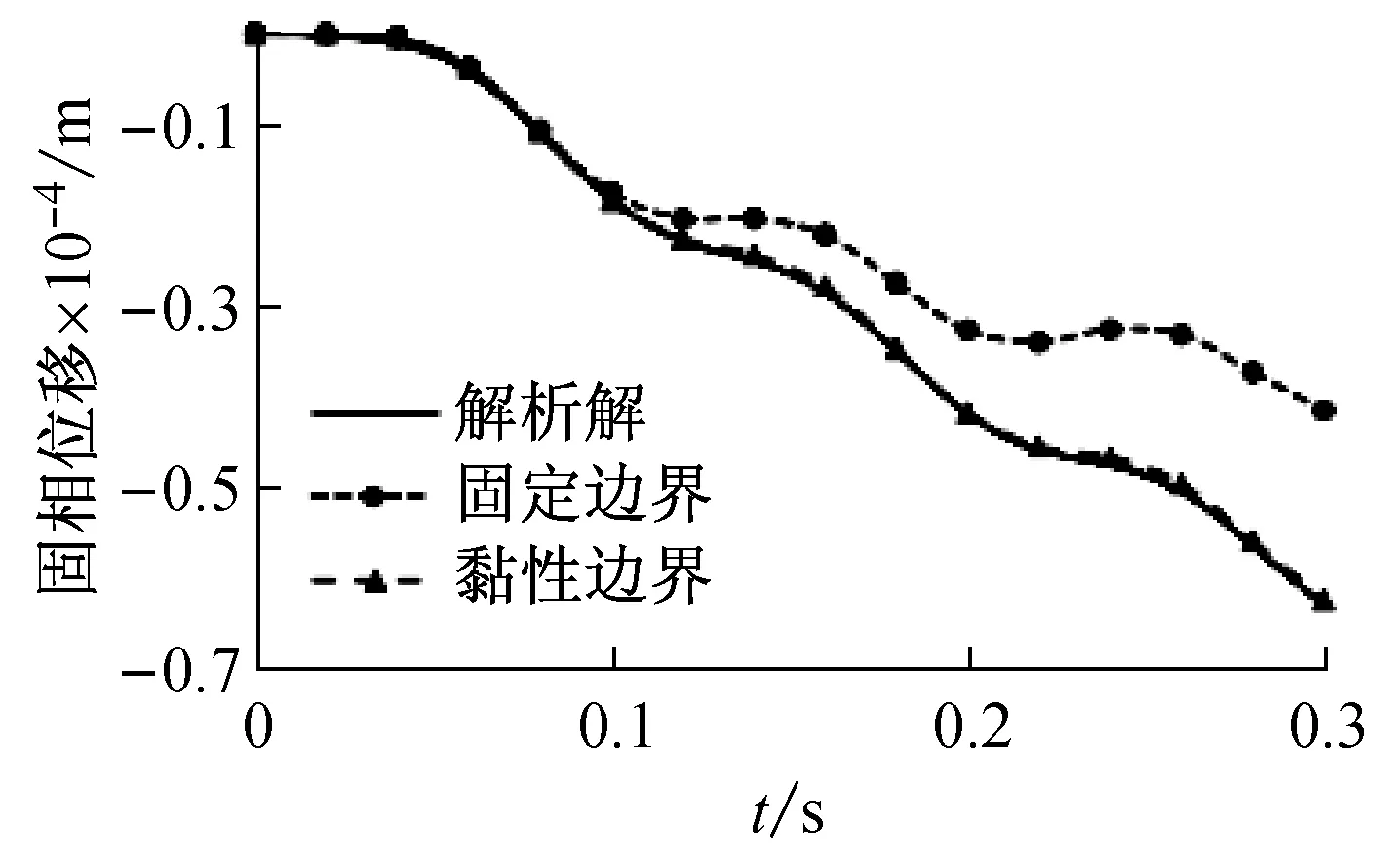
(a) z=1 m处固相位移时程曲线

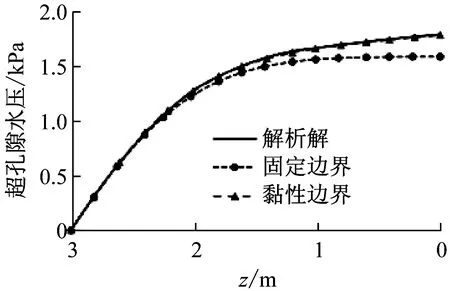
(b) t=0.15 s时超孔隙水压沿深度分布曲线

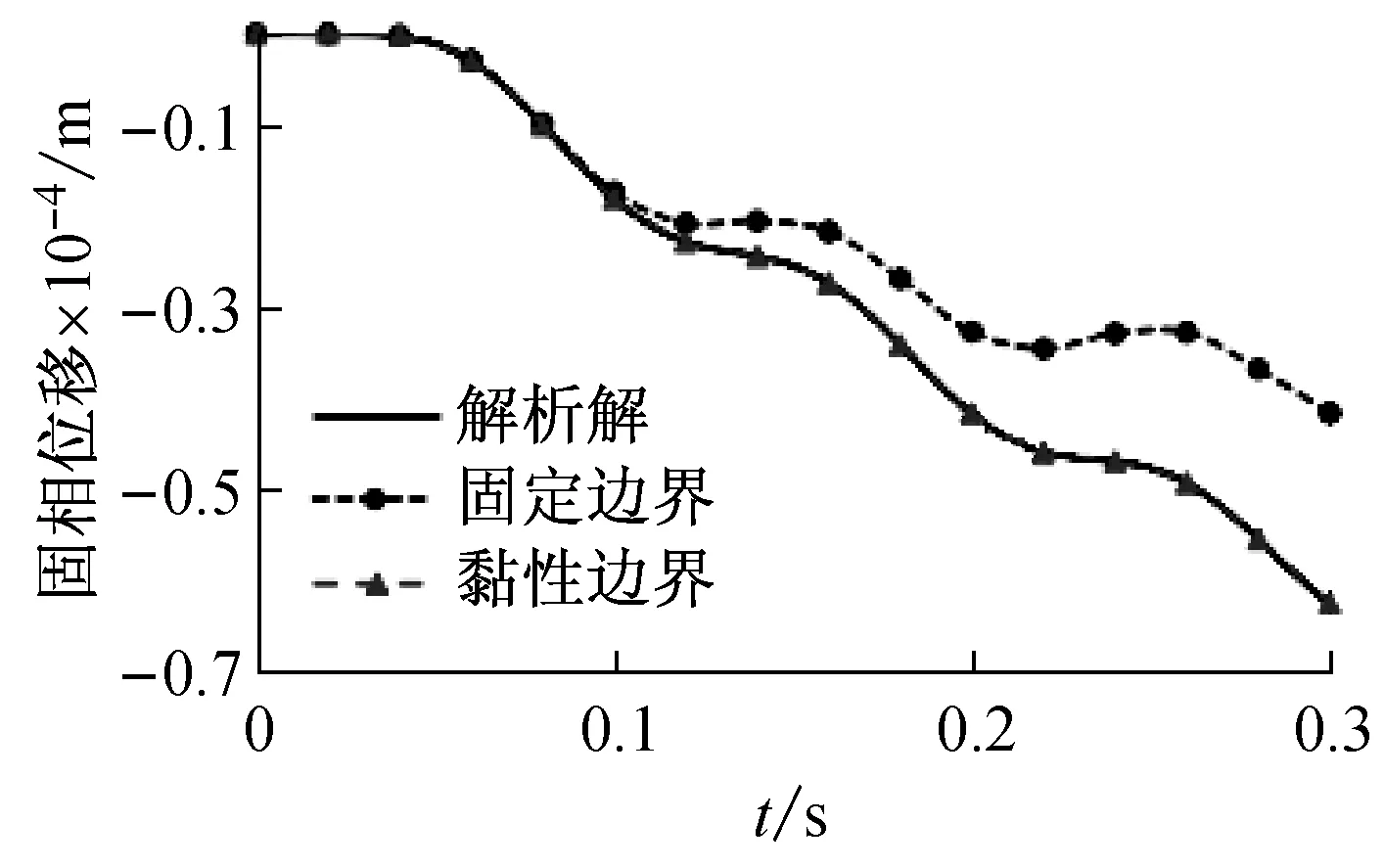
(a) z=1 m处固相位移时程曲线

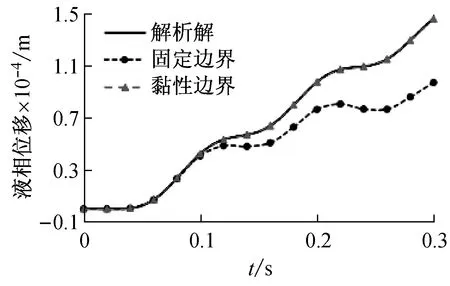
(b) z=1 m处液相位移时程曲线

3.2 模型耦合效应讨论

在饱和多孔介质中，孔隙水与土骨架的相互作用主要包括渗透力和惯性耦合力，渗透系数、荷载频率等因素是影响土骨架与孔隙水耦合效应的主要参数，由于在u-p简化形式中忽略了流体对于固相的相对加速度，因此有必要衡量不同荷载频率、不同渗透系数下u-p及u-p-U动力耦合形式的差异性。

图4为不同渗透系数下两种耦合形式的固相位移差变化规律，可以看出，在渗透系数较小时，孔隙水和固相骨架之间的相对位移比较小，产生的惯性耦合效应比较弱，在此情形下，u-p及u-p-U两种耦合形式的计算结果没有差异，可以认为渗透系数kf<10-3m/s时，惯性耦合效应可以忽略。但在渗透系数较大时，孔隙水和固相骨架之间的相对流动阻力小，两者之间形成较大的相对位移，从而表现出明显的惯性耦合效应，使得两者之间的计算结果出现差异。为考察荷载频率对惯性耦合效应的影响。图5为不同荷载频率下两种耦合形式的固相位移差变化规律。选取kf=10-6m/s以忽略渗透系数对惯性效应的影响，可以看出，随着频率的不断提高两种耦合形式的计算结果差异越来越显著，频率对饱和多孔介质应力波的传播特性有较大的影响，从上述分析可知，部分耦合形式u-p适用于渗透系数和荷载频率较小的情况。

图4 不同渗透率下两种耦合形式的固相位移差曲线

Fig.4 Solid displacement of the two dynamic formulation in differernt permeability coefficients

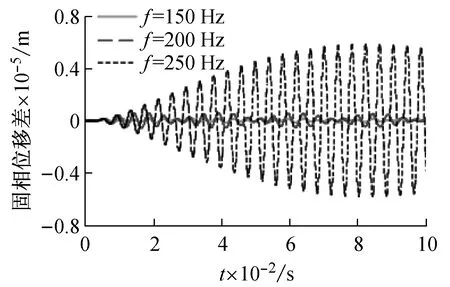
图5 不同频率下两种耦合形式的固相位移差曲线

Fig.5 Solid displacement of the two dynamic formulation in differernt frequencies

3.3 应用算例

滨海地区粉细砂地基分布广泛，且地下水位较高，粉细砂地基受到地下水影响常处于饱水状态，在工程实践中多应用动力固结法进行处理，鉴于目前有关u-p-U耦合形式的应用实例较少，本节基于此动力形式建立干砂-饱和砂层状地基耦合模型，研究冲击荷载作用下该体系的应力波传播特性。计算模型，如图6所示，饱和砂层上表面为自由透水边界，底边为固定且不透水边界，左右边界水平位移固定，材料计算参数见表2，荷载形式为三角形冲击荷载，加载周期分别为0.01 s和1 s，峰值都为1 Mpa，时间积分方法采用general-α方法，计算时间步长取0.000 1 s，采用直接求解器MUMPS进行求解。

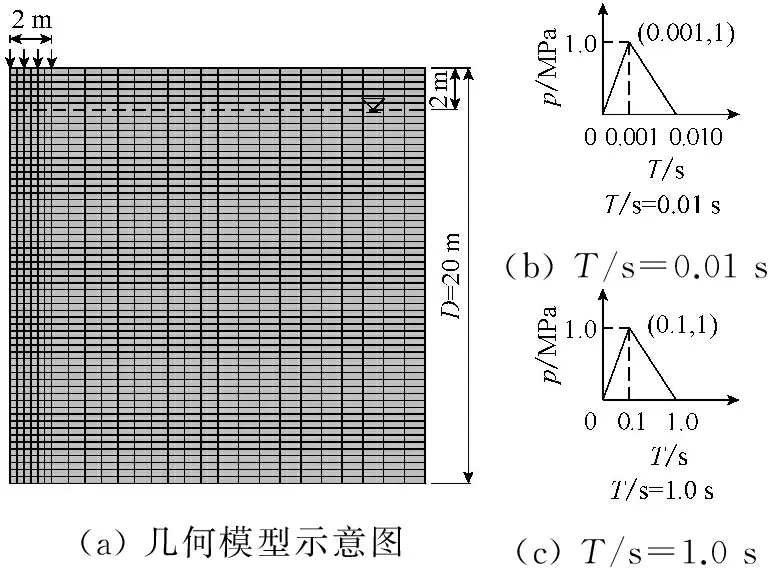
(a)几何模型示意图(b)T/s=0.01s(c)T/s=1.0s

表2 模型材料参数

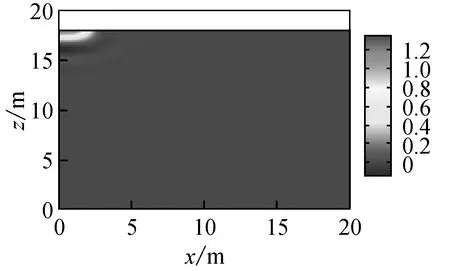
在干砂中冲击荷载激发的应力纵波传播速度为197 m/s，荷载应力峰值在12 ms时到达饱和砂区域，图7表示此时饱和砂中有效应力与超孔隙水压力的云图，由图7可知，在干砂中产生的应力波在饱和砂上部形成了超孔隙水压较高的区域，并表现出了曼德尔效应，即自由排水的上表面受到荷载作用时，会发生固结，土中的水排出，孔压消散，但是孔压不会立即消散，而是先上升后才慢慢消散。

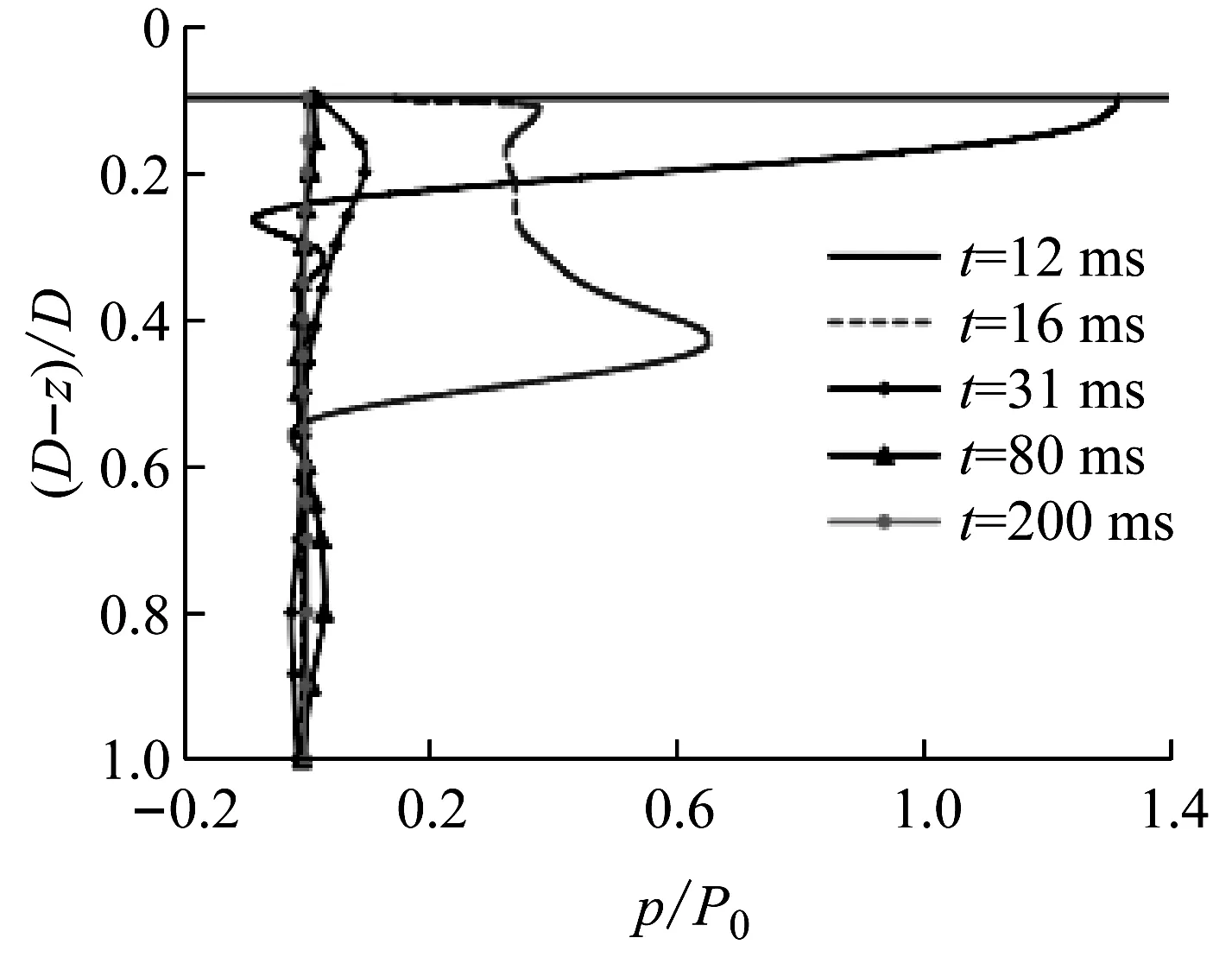
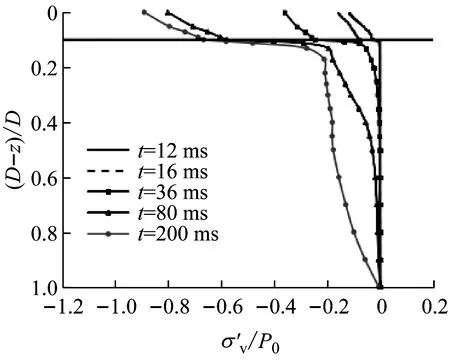
由图8可知，冲击荷载产生的能量以应力波的形式向体系内部传播，通过干砂层与饱和砂层分界面时由于介质阻抗的不同发生了明显的反射和透射现象，在饱和中快纵波和慢纵波波速大致为1 580 m/s和1 m/s，超孔隙水压的波动特性与快纵波的传播规律一致，而慢纵波波速较小且急剧衰减。由此可知，在该情形下，冲击荷载产生的应力波到达饱和砂层时有效应力迅速减少，转换为超孔隙水压以快纵波的形式进行传播，由较高的区域向深部和水平向发展，图9表示相同渗透率下荷载持续时间为1 s时，竖向有效应力与超孔隙水压力的分布图。由图可知，该情形下饱和砂中形成了明显的慢纵波，超孔隙水压峰值的传播速度大约为8 m/s，与饱和砂慢纵波的传播速度一致。

(a) 竖向有效应力

(b) 超孔隙水压

(a) 竖向有效应力

(b) 超孔隙水压

Fig.8 Normalized vertical effective stress and excess pore pressure profiles for loading duration of 0.01 s atx=1 m

由上述分析可知，不同荷载加载速率下，应力波在该体系中的传播规律表现出显著的差异性。荷载加载速率过快，荷载在干砂中产生的纵波到达饱和砂层时转化为超孔隙水压以快纵波形式进行传播，慢纵波发挥的作用不大，由于流体的压缩模量远大于土骨架的压缩模量，从而导致饱和砂中有效应力的增加幅度甚微，即快纵波对土体固结的影响不明显。当荷载加载速率减少时，形成了明显的慢纵波使得土骨架压缩从而引起孔隙水排出，但如果渗透系数较小，土骨架与孔隙水的耦合效应使得两者同时被压缩，由于流体的压缩模量远大于土骨架的压缩模量使得荷载转换为超孔隙水压的比例升高，因此，为促使饱和砂中有效应力的增加，宜提高冲击荷载的周期加载时间和土体渗透性，例如在强夯法加固地基工程实践中，采用中粗砂作为强夯垫层。目前，动力排水固结法加固软基的加固效果及其影响因素的研究仍待进一步深入开展，本文建立的数值研究方法可为动力排水固结法加固机制的研究提供一种方便快捷的手段。

(a) 竖向有效应力

Fig.9 Normalized vertical effective stress and excess pore pressure profiles for loading duration of 1 s atx=1 m

4 结 论

(1)针对u-p及u-p-U饱和多孔介质动力方程，借助COMSOL Multiphysics偏微分方程应用模式，实现了饱和多孔介质两种动力耦合方程的有限元求解，为饱和多孔介质动力响应问题提供了一种方便快捷的计算模式。

(2)通过一维饱和多孔介质动力响应解析解和本文数值解的对比分析，验证了模型求解技术的合理性和可行性，并便捷地实现了饱和多孔介质黏性边界的应用和施加，可方便地用于饱和多孔介质无限域的动力计算，两种动力耦合形式的计算结果表明部分耦合形式u-p适用于渗透系数和荷载频率较小的情况。

(3)基于u-p-U耦合形式探讨了冲击荷载作用下干砂-饱和砂地基动力固结中应力波的传播特性，计算结果表明慢纵波对动力固结的影响比较显著，合理的冲击荷载持续时间有利于固结效果的改善。

[1] BIOT M A. Theory of propagation of elastic waves in a fluid-saturated porous solid. I. Low-frequency range[J]. Journal of the Acoustical Society of America, 1956, 28(2): 168-178.

[2] BIOT M A. Theory of propagation of elastic waves in a fluid-saturated porous solid. II. Higher frequency range[J]. Journal of the Acoustical Society of America, 1956, 28(2): 179-191.

[3] BOWEN R M. Compressible porous media models by use of the theory of mixtures[J]. International Journal of Engineering Science, 1982, 20(6): 697-735.

[4] THEODORAKOPOULOS D D. Dynamic analysis of a poroelastic half-plane soil medium under moving loads[J]. Soil Dynamics and Earthquake Engineering, 2003, 23(7): 521-533.

[5] 胡安峰, 孙波, 谢康和. 下卧基岩饱和地基在移动荷载作用下的动力响应[J]. 振动与冲击, 2012, 31(4): 151-156.

HU Anfeng, SUN Bo, XIE Kanghe. Dynamic response of a saturated subgrade with rock substratum to moving loads[J]. Journal of Vibration and Shock, 2012, 31(4): 151-156.

[6] BOER D I R D, EHLERS D I W, LIU Z. One-dimensional transient wave propagation in fluid-saturated incompressible porous media[J]. Archive of Applied Mechanics, 1993, 63(1): 59-72.

[7] GAJO A, MONGIOVI L. An analytical solution for the transient response of saturated linear elastic porous media[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 1995, 19(6): 399-413.

[8] 时刚, 高广运, 冯世进. 二维及轴对称条件下饱和层状地基的Lamb问题解答[J]. 土木工程学报,2010,43(8):125-131.

SHI Gang, GAO Guangyun, FENG Shijin. The Green’s function of 2D and axisymmetric saturated layered half-space soil[J]. China Civil Engineering Journal,2010,43(8):125-131.

[9] 黄茂松, 李进军. 饱和多孔介质土动力学理论与数值解法[J]. 同济大学学报(自然科学版), 2004, 32(7): 851-856.

HUANG Maosong, LI Jinjun. Dynamics of fluidsaturated porous media and its numerical solution[J]. Journal of Tongji University (Natural Science), 2004,32(7): 851-856.

[10] SCHANZ I M, CHENG A H D. Transient wave propagation in a one-dimensional poroelastic column[J]. Acta Mechanica, 2000, 145(1): 1-18.

[11] RAHMANI A, PAK A. Dynamic behavior of pile foundations under cyclic loading in liquefiable soils[J]. Computers and Geotechnics, 2012, 40(3): 114-126.

[12] KHOSROJERDI M, PAK A. Numerical investigation on the behavior of the gravity waterfront structures under earthquake loading[J]. Ocean Engineering, 2015, 106: 152-160.

[13] ZHAO C, LI W, WANG J. An explicit finite element method for Biot dynamic formulation in fluid-saturated porous media and its application to a rigid foundation[J]. Journal of Sound and Vibration, 2005, 282(3): 1169-1181.

[15] TASIOPOULOULA P, TAIEBAT M, TAFAZZOLI N, et al. On validation of fully coupled behavior of porous media using centrifuge test results[J]. Coupled Systems Mechanics, 2015,4(1):37-65.

[16] AKIYOSHI T, FUCHIDA K, FANG H L. Absorbing boundary conditions for dynamic analysis of fluid-saturated porous media[J]. Soil Dynamics and Earthquake Engineering, 1994, 13(6): 387-397.

[17] ZIENKIEWICZ O C, SHIOMI T. Dynamic behaviour of saturated porous media; the generalized Biot formulation and its numerical solution[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 1984, 8(1): 71-96.

[18] 刘光磊, 宋二祥. 饱和无限地基数值模拟的黏弹性传输边界[J]. 岩土工程学报, 2006, 28(12): 2128-2133.

LIU Guanglei, SONG Erxiang. Visco-elastic transmitting boundary for numerical analysis of infinite saturated soil foundation[J]. Chinese Journal of Geotechnical Engineering, 2006, 28(12): 2128-2133.

[19] LI P, SONG E. A high-order time-domain transmitting boundary for cylindrical wave propagation problems in unbounded saturated poroelastic media[J]. Soil Dynamics and Earthquake Engineering, 2013, 48(5): 48-62.

[20] HAN B, ZDRAVKOVIC L, KONTOE S. Stability investigation of the Generalised-α time integration method for dynamic coupled consolidation analysis[J]. Computers and Geotechnics, 2015, 64: 83-95.

Numerical simulation for different dynamic coupling forms of saturated porous media

LIU Bao1, SU Qian1,2, LIU Ting1, LI Ting1

(1. School of Civil Engineering, Southwest Jiaotong University, Chengdu 610031, China;2. MOE Key Laboratory of High Speed Railway Engineering, Southwest Jiaotong Univeristy, Chengdu 610031, China)

Numerical simulation of dynamic behavior of saturated porous media is of great importance in many engineering problems. As pore fluid and solid skeleton interaction is hard to be decoupled, there are a lot of difficulties in numerical simulation. Aiming at characteristics of the partly coupled dynamic field equationu-pformulation and the fully coupled dynamic field equationu-p-Uformulation, the FE weak forms of the corresponding dynamic coupling control equations were derived. These FE weak forms were successfully implemented in the finite element software Comsol Multiphysics and the time domain viscous boundarys with different dynamic coupling forms were introduced in simulating unbounded saturated porous media domain. The reasonability and feassibility of the model solving technique were verified by using the analytical solution and numerical one to dynamic response of one-dimensional saturated porous meida. Finally, based onu-p-Ucoapled form, the propagating features of stress waves in the dry sandsaturated sand foundation dynamic consolidation under impacting loads were investigated. The computation results showed that the slow longitudinal were has an obvious effect on the dynamic consolidation; the reasonable time duration of impacting load is beneficial to the improvement of consolidation effects.

saturated porous media; Biot model; Comsol Multiphysics;u-pequation;u-p-Uequation

国家自然基金项目(51378441；51578467)

2015-12-30 修改稿收到日期：2016-03-01

刘宝 男，博士生，1988年生

苏谦 男，教授，博士生导师，1972年生 E-mail:suqian@126.com

TU443

A

10.13465/j.cnki.jvs.2017.09.022