基于EEMD与GA-小波神经网络的传动系声品质预测
2017-05-17黄海波黄晓蓉苏瑞强李人宪丁渭平
黄海波, 黄晓蓉, 苏瑞强, 李人宪, 丁渭平
(西南交通大学 机械工程学院,成都 610031)
基于EEMD与GA-小波神经网络的传动系声品质预测
黄海波, 黄晓蓉, 苏瑞强, 李人宪, 丁渭平
(西南交通大学 机械工程学院,成都 610031)
为了进行车辆传动系声品质预测,实施了传动系整车转鼓试验,并结合主、客观分析量化了影响传动系噪声烦恼度的主要异响指标;同时,通过相关分析揭示了心理声学客观参量与主观评价的内在关系。引入聚合经验模态分解(Ensemble Empirical Mode Decomposition, EEMD)方法与本征模态函数(Intrinsic Mode Function,IMF)样本熵值对传动系噪声特征进行了提取;在此基础上,以Morlet小波基函数作为隐含层节点的传递函数构建小波神经网络(Wavelet Neural Network,WNN),同时运用遗传算法(Genetic Algorithm, GA)优化小波神经网络的层间权值和层内阈值,构造出GA-小波神经网络模型并用于传动系声品质预测;为了对比所提取的传动系噪声特征性能,将心理声学参量也作为模型输入以进行预测,同时,为了对比GA-小波神经网络模型的预测效果,引入了传统的GA-BP神经网络模型。分析结果表明:GA-小波神经网络较GA-BP神经网络能更准确、有效地对传动系声品质进行预测,并且以本征模态函数样本熵值作为预测模型的输入特征其预测结果较心理声学参量效果更佳。
传动系;声品质;聚合经验模态分解;本征模态函数;小波神经网络
我国汽车产业已开始步入内涵式发展的稳健增长阶段,产能增长不再是主流,取而代之为车型品质的持续提升,反映到车辆声振舒适性(Noise, Vibration and Harshness,NVH)领域,即由原来单纯的“低噪声”目标要求演进为低噪声前提下对“声品质”的追求。汽车传动系作为车辆主要的传力系统,其工作方式必然会导致弯扭振动,当出现“非正常、非预期的噪声”即异响时,车辆的声品质必然会被大幅度地削弱[1]。因此,进行传动系噪声品质预测研究具有重要的意义。
目前,国内外对传动系声品质的研究较少,还处于起步阶段,主要集中于传动系振动引致的车内噪声分析。文献[2-3]针对传动系齿轮敲击噪声(Whine)进行了研究,认为齿轮敲击噪声是由于存在齿侧间隙以及发动机转矩波动,齿间出现重复冲击而产生的噪声现象,给人以“呜呜”声的感觉。文献[4]针对传动系引起的啸叫声(Squeal)进行了研究,发现啸叫主要来源于承载齿轮副与传动轴,其中齿轮啸叫是由于齿轮副动态啮合刚度、传递误差所引发的动态啮合激励噪声;传动轴啸叫是由于传动轴在高转速下自身发出的噪声。啸叫给人以高频心慌的感觉,同时具有一定的阶次性。文献[5]针对传动系振动引致的车内轰鸣声(Booming)进行了研究,指出传动系振动通过连接点传递至车身从而导致车身壁板振动可能会引发车内轰鸣声,特别当传动系模态、车身壁板模态和车内空腔声学模态耦合时最为严重,会给乘员带来焦躁不安、甚至头晕恶心的感觉。除此之外,还有文献针对传动系辐射噪声[6]、传动系部件摩擦噪声[7]等进行了研究。但以上研究工作主要为界定传动系振动引致的车内噪声,并未将其与乘员主观评价及声品质进行量化。然而,目前针对汽车声品质的研究已从整车深入到系统和零部件,如关门声品质[8]、减振器声品质[9]、喇叭声品质[10]等,但鲜有针对传动系声品质方面的研究与报道,因此,对其进行分析研究具有迫切性与现实意义。
本文通过传动系整车转鼓试验,对传动系引致的车内噪声进行了定性与定量分析,并结合相关分析找出了影响传动系声品质主观评价的主要心理声学参数。在此基础上,引入聚合经验模态分解 (Ensemble Empirical Mode Decomposition, EEMD)方法[11]构造出传动系噪声主要特征向量,并将其与经过遗传算法(Genetic Algorithm, GA)[12]参数优化的小波神经网络(Wavelet Neural Network)模型结合进行传动系声品质预测。为了验证所构造特征的性能,将心理声学参量也作为预测模型的输入特征进行比较,同时引入了GA-BP神经网络进行对比分析。通过比较分析,发现基于EEMD与GA-小波神经网络的方法预测效果更佳,可为今后传动系噪声评价和声品质预测提供参考。
1 传动系噪声测试及其主观评价
1.1 传动系噪声样本采集
为了减小路噪、风噪等背景噪声带来的干扰,汽车传动系噪声测试在整车半消声室内的转鼓上进行。试验参照国标GB/T 18697—2002[13]中的传感器布置方法,采用LMS SCADAS SM24噪声信号采集与回放系统和40AE传声器记录车内驾驶员耳旁噪声信号,如图1所示。数据采集参数设置如下:采样频率44 100 Hz,频率分辨率为1 Hz,采样时间15 s。用3款不同车型的前置后驱MPV汽车,分别以三挡缓加速方式由40 km/h加速到100 km/h、三挡匀速50 km/h、四挡匀速70 km/h和五挡匀速100 km/h进行整车转鼓试验并采集车内噪声信号。
通过时域采集的噪声样本,导入到LMS Test Lab 13A数据处理软件。考虑到噪声样本过少缺乏统计性,而噪声样本过多会增加评价人员疲劳度从而导致评价准确率降低。本文通过高性能耳机回放,选出具有代表性的加速过程噪声样本6组,匀速过程噪声样本90组。其中加速过程噪声样本由具有经验的主观评价人员选出的带有传动系敲击声、啸叫声和轰鸣声噪声信号各2组;匀速过程噪声样本由具有不同类型、不同程度异响的传动系噪声信号组成,同时在各挡位和速度下的样本组数分布均匀。将选取的噪声信号在CoolEdit软件中分别截取成长度为10 s的噪声样本,并对匀速工况噪声信号分别通过发动机转速基频和二阶频率FFT (Fast Fourier Transformation)带阻滤波,作为进行后续主、客观分析的数据。
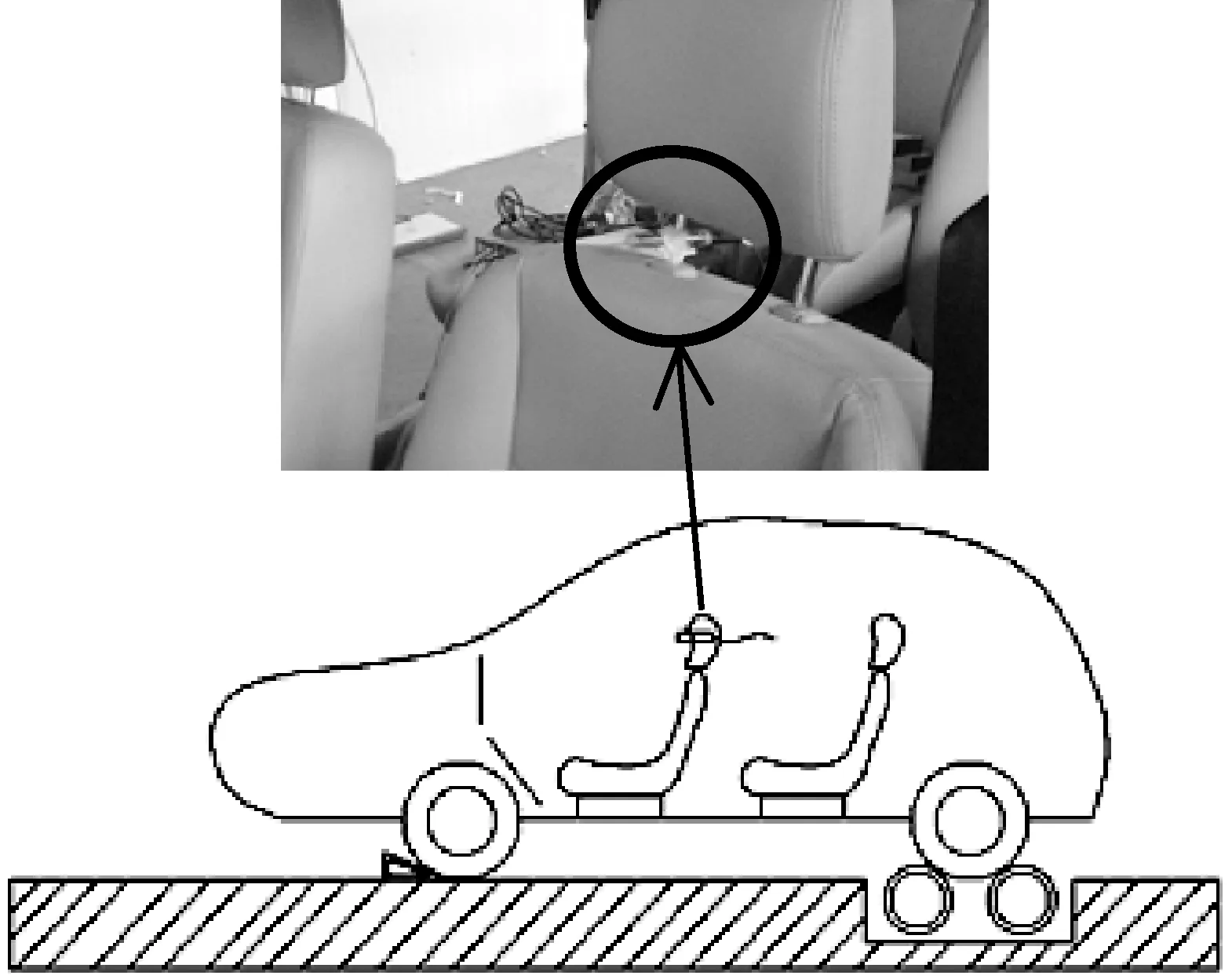
图1 整车转鼓试验示意图
1.2 传动系噪声品质主观评价
由于传动系噪声的特殊性,目前尚无联系传动系声品质与主观烦恼度的统一指标,为了给传动系噪声品质主观评分提供参考,首先进行了传动系异常噪声程度的评价实验。由于汽车在加速过程中车内噪声较为丰富,容易激发传动系异响,因此首先对通过整车转鼓试验收集到的6组不同类型传动系异响噪声样本进行主观评价,以此对传动系声品质进行定性分析。需要说明的是,由于汽车加速工况下车内噪声属于非平稳信号,即传动系异响时刻与程度具有随机性,不宜作为声品质客观分析数据。因此,为了对传动系声品质进行准确的定量分析,需采用匀速工况下收集的传动系噪声样本作为最终的主、客观评价数据进行分析。
选取28名听力正常、身体健康的在校学生作为主观评审团实施评价实验,其中男性15名,女性13名。首先采用排序法[14]进行传动系声品质定性分析,即对分别含有敲击声、啸叫声和轰鸣声的传动系加速噪声样本进行主观烦恼度排序。具体而言,每位主观评价人员对以上3种传动系异常噪声烦恼度进行排序,然后将各类噪声的排序结果进行统计,即统计传动系异响类型在排序中的计数数目。评价结果如图2所示,可知,从主观烦恼度的角度出发,不同评价人员对传动系声品质的感知具有差异性,但统计结果表明传动系轰鸣声较啸叫声烦躁,且两者的烦躁度都要强于敲击声。结合等级评分法[15]制定传动系声品质主观评价表如表1所示。然后主观评审团根据表1并参考传动系噪声品质定性分析结果对整车转鼓试验收集并后处理得到的90组匀速工况噪声样本进行精细化评分。对每个噪声样本的全部主观评分取算数平均值作为该样本的最终得分,并计算其对应的主观评分误差棒(Error Bar)[16],如图3所示。由评价结果可知,评审人员的主观评分较为稳定,其Kendall协和系数达到0.841。

图2 传动系异响强弱烦恼度计数统计
表1 传动系声品质主观评价表
Tab.1 Subjective evaluation form of the powertrain sound quality

传动系噪声品质烦恼度毫不烦恼有点烦恼比较烦恼非常烦恼评分等级1234
因此,该主观评价实验有效,可作为后续分析的基础。
2 基于心理声学的传动系声品质评价
心理声学参数(如响度、尖锐度、粗糙度等)能较好地反映人的主观听觉感受,所以研究中常常将其作为噪声品质的客观评价指标。对经过后处理得到的90组匀速工况噪声样本分别通过LMS test Lab 13A计算其心理声学参数—响度、尖锐度、粗糙度、抖动度,以及物理声学参数—A计权声压级、线性声压级,所得部分结果如表2所示。
为了研究传动系噪声品质主、客观评价之间的关系,对等级评分法得到的传动系噪声主观评价得分与声学客观参量进行相关分析。利用SPSS 20软件计算其相关系数,如表3所示,同时绘出主、客观评价相关散点图,如图4所示。

图3 传动系声品质主观评分汇总(“o”为主观评分平均值,“I”为主观评分误差棒)
Fig.3 Subjective evaluation scores for the powertrain sound quality (‘o’ is the average value of subjective evaluation scores, “I” is the error bar)

表2 传动系噪声品质客观参数

表3 主观评价与客观参数相关性
由表3与图4可知,传动系声品质的主观评价与粗糙度、尖锐度的相关系数高于0.7,显著性水平小于0.01,具有一定的线性关系,与响度、抖动度的相关系数分别为0.645 8和0.616 5,线性相关性较弱,而与A计权声压级、线性声压级的相关系数都低于0.6,表明主观评价与两者的相关性较差。这主要是因为传动系引致的车内轰鸣声一般在20~100 Hz范围内[17],同时轰鸣声亦为影响传动系声品质主观评价较大的噪声类型,而粗糙度指标适用于70 Hz内的调幅调频信号,使得主观评分与粗糙度的相关性较高。同样,传动系啸叫声主要分布于300~4 000 Hz范围内[18],而尖锐度对高频信息敏感,导致其与主观评分的相关系数亦较高。传动系齿轮敲击声相对于轰鸣声和啸叫声对主观评分的影响较小,而抖动度适用于20 Hz内的低频调制信号,亦能提取出部分敲击声特征信息。基于临界频带的响度计算对低频的划分较细,也可在一定程度上反映传动系声品质的烦恼度特性。A计权声压级与主观评分相关系数为0.552 7,不易判定两者之间是否存在线性关系,而线性计权声压级与主观评分的相关系数为0.359 1,几乎没有线性相关性。因此,考虑到传动系声品质与主观评价之间的复杂关系,现引入适合稳态、非稳态信号处理的聚合经验模态分解 (EEMD)方法与非线性映射能力较强的神经网络方法进行传动系噪声品质预测研究。

(a) 响度与主观评价相关散点图
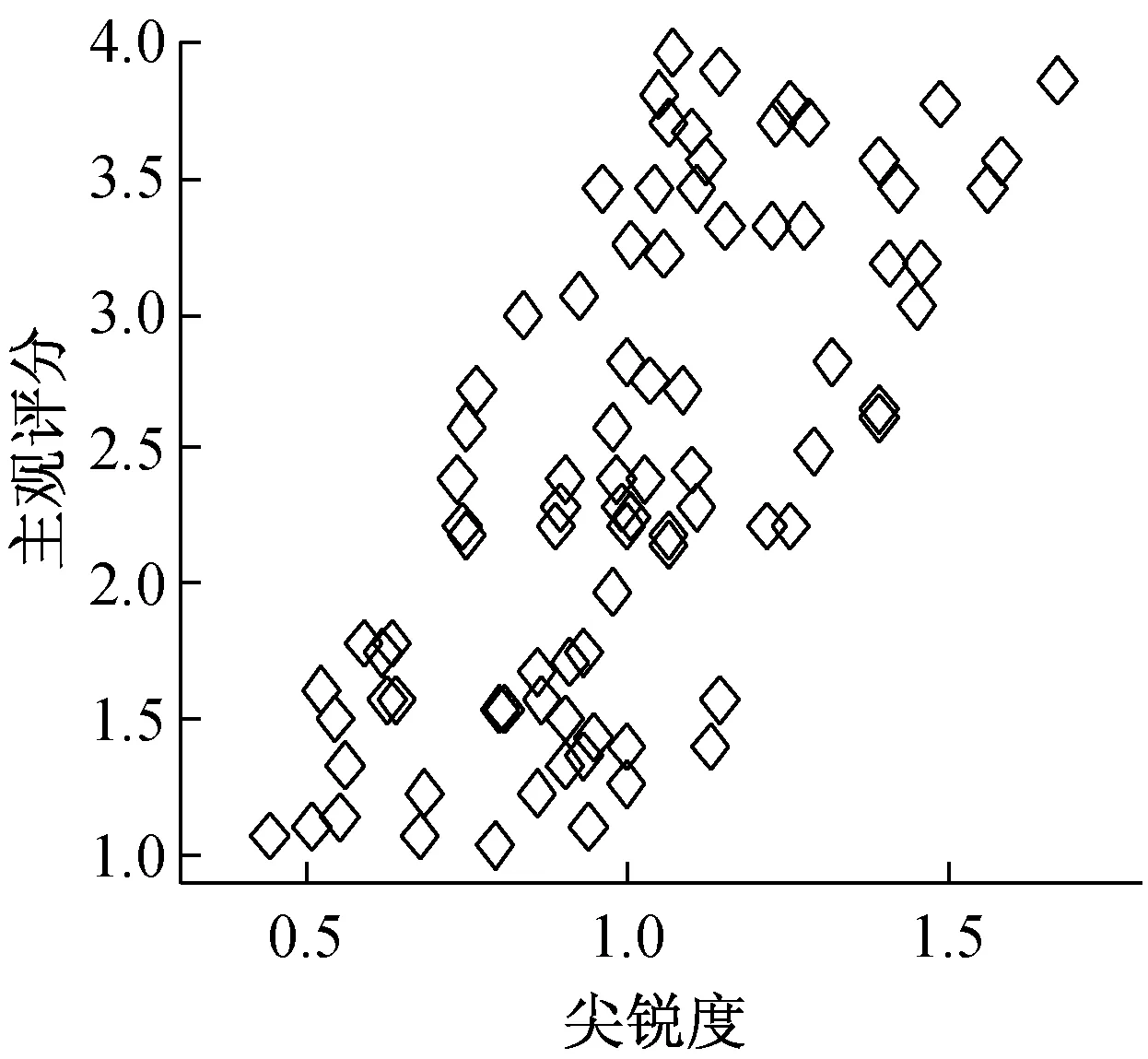
(b) 尖锐度与主观评价相关散点图

(c) 抖动度与主观评价相关散点图

(d) 粗糙度与主观评价相关散点图

(e) A计权声压级与主观评价相关散点图

(f) 线线计权声压级与主观评价相关散点图
3 基于EEMD与GA-小波神经网络的传动系声品质预测
3.1 基于EEMD的传动系噪声信号特征构造
3.1.1 EEMD
EEMD是在EMD(Empirical Mode Decompo- sition)[19]的基础上改进得到的一种自适应非平稳信号处理方法。不同于小波分解、小波包分解等方法,EEMD不依赖于基函数的选取,仅根据数据自身的时间尺度特征来进行信号分解,从而生成一系列具有不同特征尺度的数据序列—征模态函数(Intrinsic Mode Function, IMF)。本征模态函数是具有单分量物理意义的一类信号,代表了一个简单的固有特征模式。EEMD分解方法的核心在于利用高斯白噪声零均值的特点,在实测信号中加入具有一定幅值系数的高斯白噪声,然后对加入高斯白噪声的信号进行EMD分解从而得到若干本征模态函数,在此即完成一次EEMD迭代。根据设置的迭代次数反复对重新加入高斯白噪声的信号进行EMD计算,最后将各层IMF分别进行线性平均即得到最终的新IMF,该方法得到的新IMF经过高斯白噪声消噪从而成为更加持久稳固的真实信号。经过EEMD分解后的信号与各IMF关系为
(1)
式中:x(t)为原始信号;IMFi为各层本征模态函数;r为趋势项;n为分解的IMF个数。
3.1.2 传动系噪声信号特征构造
为了进行传动系声品质预测,需对传动系噪声信号特征进行构造。由于EEMD能从时频角度对非平稳信号进行自适应处理,因而特别适合进行机械噪声、振动信号分析。传动系噪声信号特征构造具体过程如下:
步骤1 滤波,首先对噪声信号样本进行高通滤波,消除20 Hz以下的声音信号。
步骤2 EEMD分解,对滤波后的声信号进行EEMD分解,设置EEMD聚合迭代次数为100次,由于目前暂无指导高斯白噪声幅值系数的选取原则,所以根据研究经验[20]取其值为0.4,由此计算得出n个本征模态函数IMFi,i=1,2,…,n。1号噪声样本的EEMD分解结果,如图5所示。
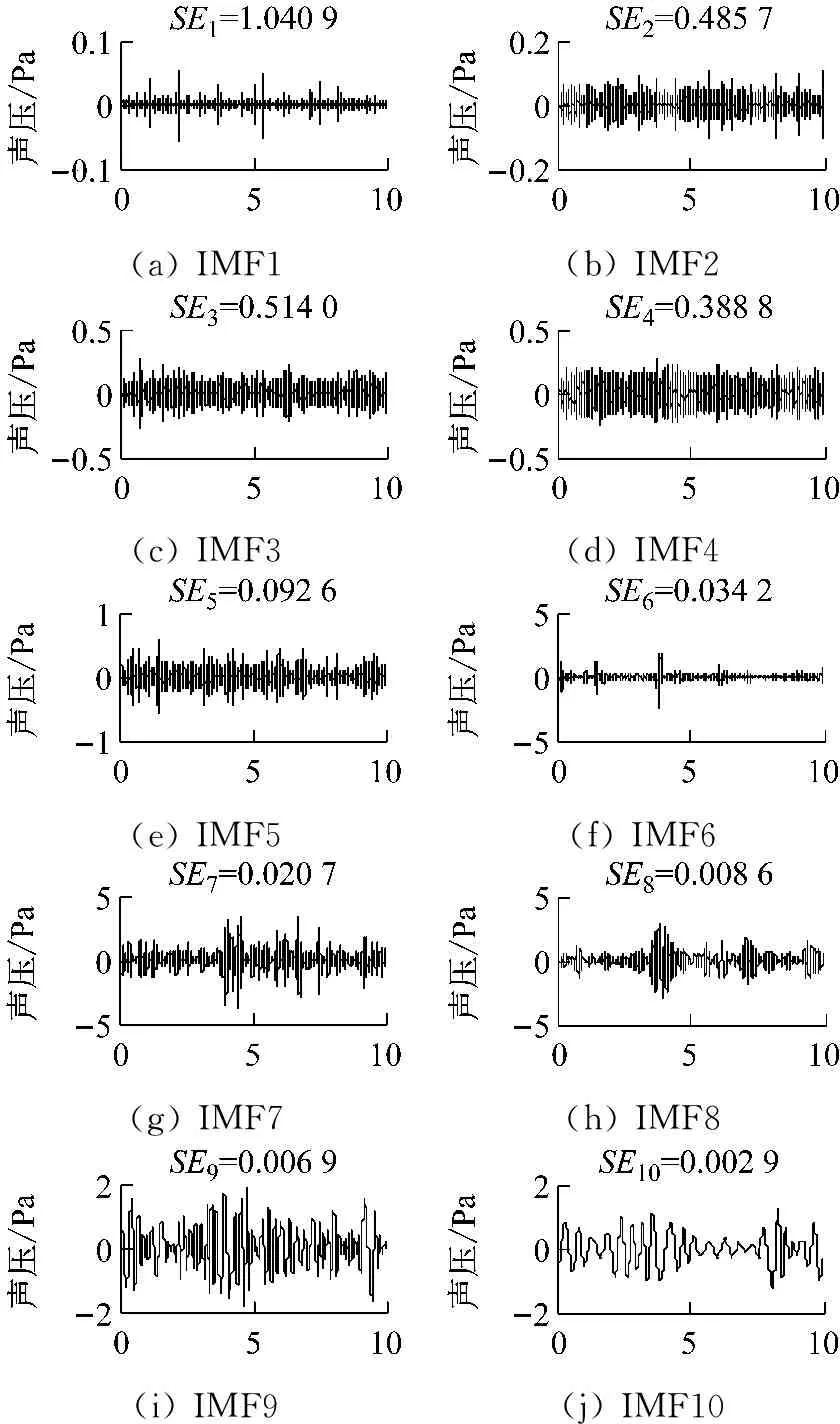
(a)IMF1(b)IMF2(c)IMF3(d)IMF4(e)IMF5(f)IMF6(g)IMF7(h)IMF8(i)IMF9(j)IMF10
图5 1号噪声样本的EEMD分解及计算结果
Fig.5 The EEMD decomposition and post-processing
result of 1# noise signal
步骤3 特征构造。传动系异响从某种意义上讲为车内正常噪声之外的新信息,该新信息导致了不同传动系声品质主观评价之间的差异,而样本熵作为一种量化时间序列复杂性的度量方法,其从物理意义上讲是度量序列产生新信息的量,因此可通过样本熵来构造传动系噪声信号特征。样本熵的计算方法可参考文献[21],据此可得各本征模态函数的样本熵特征值SEi计算如式(2)所示
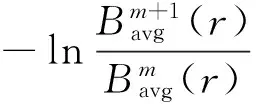
(2)
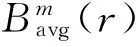
SE=(SE1,SE2,…,SEn)
(3)
3.2 GA-小波神经网络模型建立
3.2.1 小波神经网络
小波神经网络是一种以BP(Back Propagation)神经网络拓扑结构为基础,以小波基函数代替传统sigmoid函数作为隐含层节点传递函数的一种非线性神经网络。由于小波基函数具有正交性、紧支性、对称性等优点,可在一定程度上提升传统神经网络的抗噪性和泛化性。本文选择Morlet小波函数作为模型隐含层的传递函数,构造出的小波神经网络拓扑结构,如图6所示。
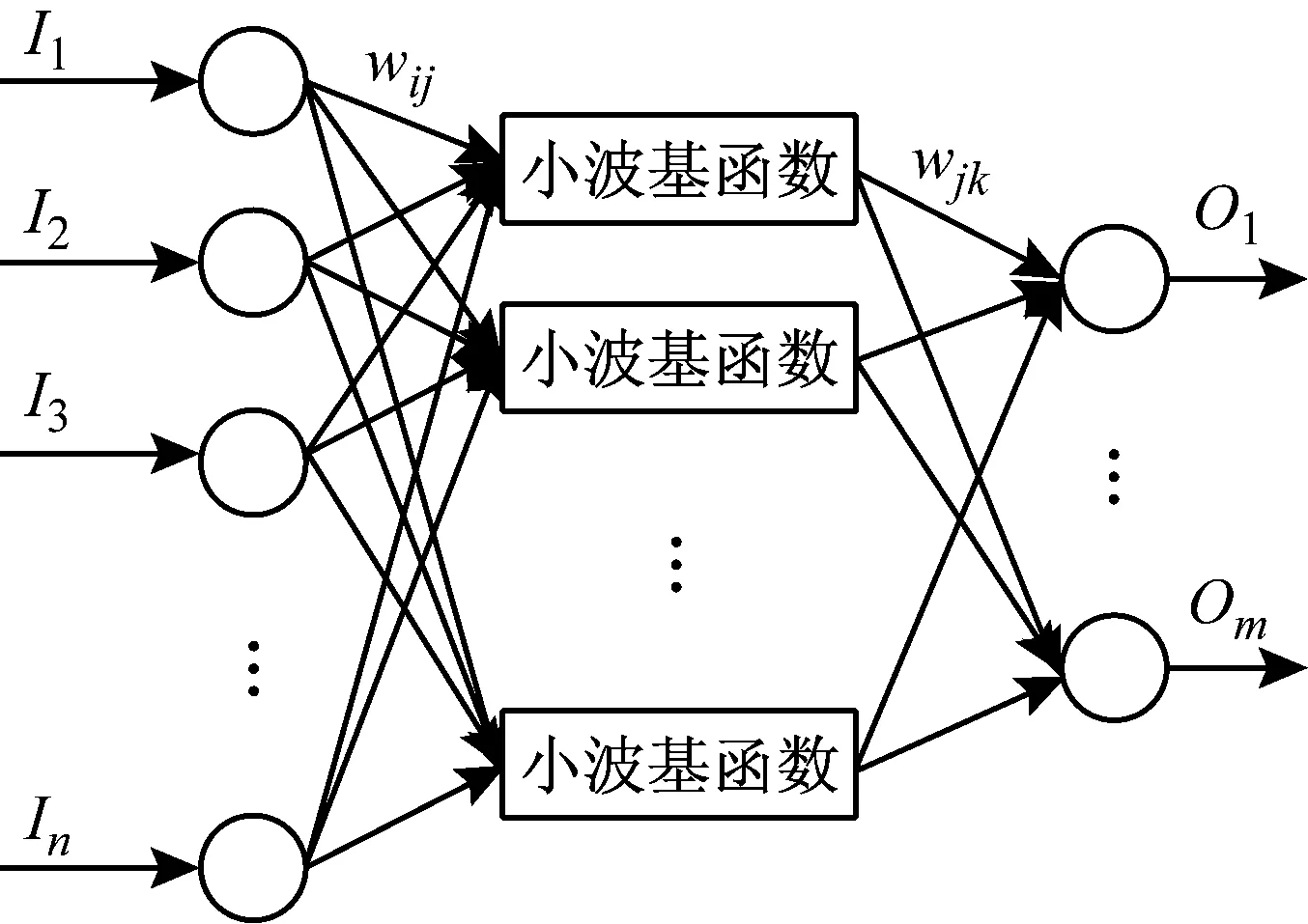
图6 小波神经网络拓扑结构图
当输入数据序列为Ii(i=1,2,…,n)时,小波神经网络的隐含层输出公式为
(4)
式中:h(j)为隐含层第j个节点的输出值;Фj为Morlet小波基函数;wij为输入层与隐含层之间的连接权值;bj和aj分别为小波基函数的平移因子与伸缩因子,在此作为隐含层阈值;l为隐含层节点数目。基于此,可得到小波神经网络的输出层计算公式为
(5)
式中:wjk为隐含层与输出层之间的连接权值;m为输出层节点数目。
3.2.2 GA-小波神经网络模型
小波神经网络根植于BP神经网络,本质上仍是前馈型神经网络,其层间权值及层内阈值为随机初始化,这会导致网络性能不稳定,甚至出现两极分化。因此,现引入智能算法优化小波神经网络的初始权值和阈值。常用的智能算法有遗传算法(GA)、蚁群算法(Ant Colony Optimization, ACO)、粒子群算法(Particle Swarm Optimization, PSO)等,这里采用遗传算法进行网络参数优化。遗传算法把生物进化的原理引入优化参数形成的编码串联群体中,按照所定义的适应度函数并通过遗传中的选择、交叉和变异对个体进行筛选,使适应度好的个体被保留,差的被淘汰,新的群体既继承了上一代的信息,又优于上一代。通过反复循环迭代,直至满足终止条件。遗传算法优化小波神经网络主要分为:小波神经网络结构确定、遗传算法优化网络参数、模型训练及预测,其算法流程如图7所示,具体计算过程为
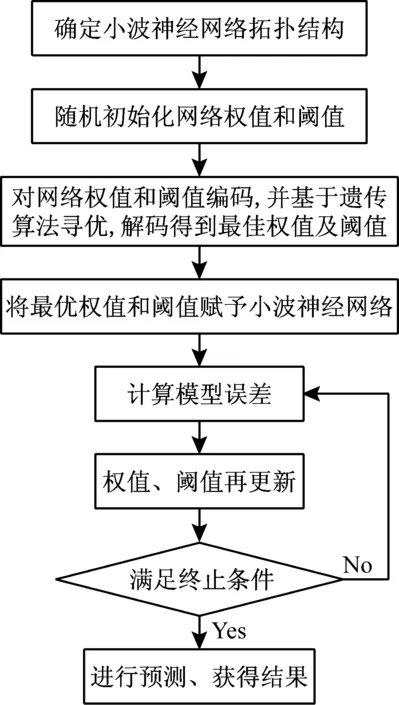
图7 GA-小波神经网络算法流程图
步骤1 小波神经网络结构确定。小波神经网络结构包含网络输入层、隐含层和输出层的节点数目。其中输入层节点数目等于输入样本维数;输出层节点数目等于输出向量维数;隐含层节点数目目前没有统一的选取原则,一般按照式(6)进行确定
nh=2×nin+1
(1)
式中:nh为隐含层节点数目;nin为输入层节点数目。
步骤2 遗传算法优化网络参数。小波神经网络需要优化的参数为网络的层间权值和层内阈值,首先对初始化的权值与阈值进行编码,然后通过小波神经网络对训练数据进行训练并将计算误差作为适应度值,接下来进行选择、交叉、变异计算新群体的适应度值,通过反复迭代,当达到终止条件时即可对染色体进行解码,最终得到最佳的小波神经网络权值和阈值初始值。这里设置的遗传算法参数如表4所示。

表4 遗传算法主要参数设置
步骤3 模型训练及预测。获得经过遗传算法优化的网络初始权值和阈值后,将其赋予新建立的小波神经网络,即可根据具体情况对样本数据进行训练及预测。
通过步骤1~步骤3可建立GA-小波神经网络模型,并将其用于传动系声品质预测。
3.3 传动系噪声品质预测及对比分析
将构造的IMF样本熵特征向量作为GA-小波神经网络的输入数据,传动系噪声主观评分作为网络的输出数据,进行传动系声品质预测。由于构造的IMF样本熵特征向量为10维,所以根据式(6)构建的GA-小波神经网络结构为10-21-1。为了对比提取的IMF样本熵特征性能,现将与传动系噪声主观评价相关性较高的心理声学参数响度、尖锐度、粗糙度和抖动度也作为模型的输入特征,重新构建新的GA-小波神经网络模型进行传动系声品质预测,并由式(6)确定其结构形式为4-9-1。同时,为了检验GA-小波神经网络的性能,在此引入传统的GA-BP神经网络模型进行对比分析,其中遗传算法参数和BP神经网络模型结构同GA-小波神经网络,并采用sigmoid 函数作为节点传递函数。将1号~60号噪声样本作为训练数据,61号~90号样本作为测试数据,分别采用归一化后的IMF样本熵特征向量与心理声学参量作为特征输入进行传动系声品质预测。由于遗传算法与神经网络求解的非唯一性,文中所有实验均运行50次并求取结果均值,所得测试集预测结果如图8所示,预测误差如图9和表5所示。
由图8和图9可知,GA-小波神经网络和GA-BP神经网络与所提取的输入特征结合能够对传动系声品质进行较好地预测,并且能够通过给定的样本信息权衡模型学习能力与样本识别精度。由表5可知,对于GA-小波神经网络,将IMF样本熵特征作为模型输入获得的预测结果其决定系数为0.966 5,均方根误差为0.863 2,均优于心理声学参量作为输入的预测效果,同时,对于GA-BP神经网络也有类似的特点。这表明经由本征模态函数与样本熵构造出的声信号特征较心理声学参量更适合作为传动系声品质预测模型的输入特征。另外,在输入特征一定的条件下,基于GA-小波神经网络的预测结果其决定系数与各项预测误差均优于GA-BP神经网络。这表明小波基函数作为隐层节点传递函数可以提升模型的鲁棒性与泛化性。值得一提的是,虽然GA-BP神经网络性能稍逊于GA-小波神经网络,但是当IMF样本熵特征向量作为GA-BP神经网络输入而声品质参量作为GA-小波神经网络输入时,前者的预测效果优于后者。这表明对于特定的回归问题,其输入特征的优劣对于预测效果具有重要性,同时进一步体现IMF样本熵相较声品质参量能更有效地提取出传动系声品质特性。因此,针对车辆传动系声品质评价问题,通过IMF样本熵与GA-小波神经网络既能对其进行准确且有效地预测。

图8 传动系声品质预测结果
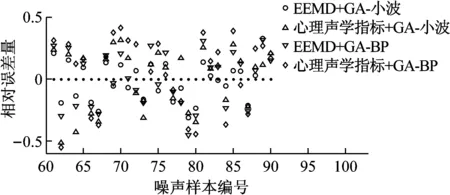
图9 传动系声品质预测结果相对误差量(相对误差量=预测值-真实值)
Fig.9 The relative error between the predicted and the real-evaluated powertrain sound quality (relative error = prediction values-real-evaluated values)

表5 各预测模型所得预测误差对比
4 结 论
(1) 通过传动系整车转鼓试验采集了加速工况噪声信号,基于此对传动系引致的车内主要异常噪声进行了定性分析,结果表明传动系轰鸣声、啸叫声和敲击声对主观烦恼度的影响依次降低。同时,通过传动系整车转鼓试验采集了匀速工况噪声信号,并对传动系引致的车内噪声进行了定量分析,找出了对传动系声品质主观评价影响较大的主要心理声学参数,为粗糙度和尖锐度。
(2) 构建了基于Molert小波基的小波神经网络作为传动系声品质预测模型,并通过遗传算法优化其层间权值和层内阈值。通过EEMD对采集并后处理得到的噪声信号进行分解,获得相应的本征模态函数—IMF,计算各IMF对应的样本熵值并构造出传动系声品质特征向量。为了验证所构造的传动系噪声特征性能,将与主观评价相关系数较高的心理声学参数也作为模型输入特征进行分析。预测结果表明IMF样本熵更适合作为传动系声品质特征向量。
(3) 为了对比GA-小波神经网络的性能,引入了传统的GA-BP神经网络进行声品质预测,结果表明在输入特征相同的条件下,GA-小波神经网络的预测准确性与鲁棒性均优于GA-BP神经网络。
[1] 吴光强,栾文博. 汽车传动系相关 NVH 问题的动力学研究论述[J]. 机械工程学报,2013,49(24):108-115.
WU Guangqiang, LUAN Wenbo. Review of dynamic research for NVH problems related to automotive driveline [J]. Journal of Mechanical Engineering, 2013, 49(24): 108-115.
[2] WANG M Y, MANOJ R, ZHAO W. Gear rattle modelling and analysis for automotive manual transmissions [J]. Proceedings of the Institution of Mechanical Engineers, Part D:Journal of Automobile Engineering, 2001, 215(2):241-258.
[3] KIM E Y, SHIN T J, LEE S K. New tonality design for non-stationary signal and its application to sound quality for gear whine sound[J].Proceedings of the Institution of Mechanical Engineers, Part D: Journal of Automobile Engineering, 2013,227(3): 311-322.
[4] CURTIS S, PEARS J, PALMER D. An analytical method to reduce gear whine noise, including validation with test data [C]//Society of Automotive Engineers. SAE Technical Papers. Warrendale:SAE International, 2005: 1819-1824.
[5] LEE S K. Objective evaluation of interior sound quality in passenger cars during acceleration [J]. Journal of Sound and Vibration, 2008,310(1/2): 149-168.
[6] WANG Y S, LEE J M, KIM D G, et al. Sound quality prediction for nonstationary vehicle interior noise based on wavelet pre-processing neural network model [J]. Journal of Sound and Vibration, 2007, 299: 933-947.
[7] 周广武,王家序,李俊阳,等. 低速重载条件下水润滑橡胶合金轴承摩擦噪声研究[J]. 振动与冲击,2013,32(20):14-17.
ZHOU Guangwu, WANG Jiaxu, LI Junyang, et al. Friction-induced noise of a water lubricated rubber alloy bearing under low speed and heavy duty[J]. Journal of Vibration and Shock, 2013, 32(20): 14-17.
[8] 杨川,于德介. 基于伪Wigner-Ville分布的汽车关门声品质评价参数研究[J]. 机械工程学报,2011,47(24):91-96.
YANG Chuan,YU Dejie. Research on the sound metric of door slamming sound based on pseudo Wigner-Ville distribution[J]. Journal of Mechanical Engineering, 2011, 47(24): 91-96.
[9] 黄海波,李人宪,丁渭平,等. 基于EMD-WVD的车辆悬架减振器异响声品质客观评价研究[J]. 振动与冲击,2015,34(18):154-160.
HUANG Haibo, LI Renxian, DING Weiping, et al. Research on the objective sound quality of vehicle suspension shock absorber abnormal noise based on EMD-WVD [J]. Journal of Vibration and Shock, 2015, 34(18): 154-160.
[10] 徐中明,张芳,贺岩松,等. 汽车喇叭声品质分析[J]. 汽车工程,2012,34(2):149-153.
XU Zhongming, ZHANG Fang, HE Yansong, et al. An analysis on the sound quality of car horns [J]. Automotive Engineering, 2012, 34(2): 149-153.
[11] WU Z, HUANG N E. Ensemble empirical mode decom-position: a noise-assisted data analysis method [J]. Advances in Adaptive Data Analysis, 2009, 56(1): 19-41.
[12] RICCAR D, LEA R. Genetic algorithms in chemistry[J]. Journal of Chromatography A, 2007, 1158(1/2): 226-233.
[13] Acoustics-method for measuring vehicle interior noise: GB/T 18697—2002[S].2002.
[14] WANG Y S, SHEN G Q, GUO H, et al. Roughness modelling based on human auditory perception for sound quality evaluation of vehicle interior noise[J]. Journal of Sound and Vibration, 2013, 332(16): 3893-3904.
[15] KIM H W, LEE S K, NA E W. Sound quality evaluation of the impact noise induced by road courses having an impact bar and speed bumps in a passenger car[J]. Proceedings of the Institution of Mechanical Engineers, Part D: Journal of Automobile Engineering, 2010, 224(6): 735-747.
[16] LEE S, KIM H, NA E. Improvement of impact noise in a passenger car utilizing sound metric based on wavelet transform[J]. Journal of Sound and Vibration, 2010,329(17):3606-3619.
[17] SHIN S H, IH J G, HASHIMOTO T, et al. Sound quality evaluation of the booming sensation for passenger cars [J]. Applied Acoustics, 2009, 70(2): 309-320.
[18] FIETKAU P, BERTSCHE B. Influence of tribological and geometrical parameters on lubrication conditions and noise of gear transmission[J]. Mechanism and Machine Theory, 2013, 69(8):303-320.
[19] HUANG N E, SHEN Z. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis [ J ]. Procedures of the Royal Society of London, Series A, 1998,454: 903-995.
[20] WU Z H, HUANG N E. A study of the characteris tics of white noise using the empiricalmode decomposition method[J]. Proceedings of the Royal Society A Mathematical Physical Engineering Science, 2004, 460: 1579-1611.
[21] 赵晓华,许士丽,荣建,等.基于Roc曲线的驾驶疲劳脑电样本熵判定阈值研究[J].西南交通大学学报,2013,48(1):178-183.
ZHAO Xiaohua, XU Shili, RONG Jian, et al. Discriminating threshold of driving fatigue based on the electroencephalography sample entropy by receiver operating characteristics curve analysis [J]. Journal of Southwest Jiaotong University, 2013, 48(1): 178-183.
Sound metric prediction of a power train system based on EEMD and GA-wavelet neural network
HUANG Haibo, HUANG Xiaorong, SU Ruiqiang, LI Renxian, DING Weiping
(College of Mechanical Engineering, Southwest Jiaotong University, Chengdu 610031, China)
To predict the sound quality of a vehicle power train system’s noise, a complete vehicle drum test was conducted. Combining subjective analysis and objective one, six sound indices for the power train system’s noise annoyance level were quantified. Via the correlation analysis, internal relations between the six psychoacoustic objective parameters and the subjective evaluation were revealed. Features of the power train system’s noise were extracted by using the ensemble empirical mode decomposition (EEMD) method, and the intrinsic mode function sample entropy. The Morlet wavelet basis functions were used as the transfer function of hidden layers to develop a wavelet neural network. In addition, the genetic algorithm was applied to optimize weights between layers and thresholds within layers so that a GA-wavelet neural network was developed to predict the sound quality of the power train systems’s noise. In order to validate the the newly extracted power train system’s noise features, the psychoacoustic parameters were also taken as the model’s inputs to predict the sound quality. Meanwhile, the conventional GA-BP neural network was also introduced to compare its performances with those of the GA-wavelet neural network. The results showed that the GA-wavelet neural network can predict the sound quality of the power train system’s noise more accurately and effectively than the GA-BP neural network can; the intrinsic mode function sample entropy values are better than the psychoacoustic parameters to be taken as the input features of the prediction model.
power train system; sound metric; ensemble empirical mode decomposition(EEMD); intrinsic mode function; wavelet neural network
国家自然科学基金(51475387);四川省重点研发科技计划项目(2015GZ0126)
2015-12-09 修改稿收到日期:2016-03-21
黄海波 男,博士生,1989年生
丁渭平 男,博士,教授,1968年生
U467.1+1
A
10.13465/j.cnki.jvs.2017.09.020
