一种滚动轴承特征频率的自动识别方法研究

高大为， 朱永生， 刘煜炜， 曹鹏辉， 高 闯

(西安交通大学 现代设计与转子轴承教育部重点实验室，西安 710049)

一种滚动轴承特征频率的自动识别方法研究

高大为， 朱永生， 刘煜炜， 曹鹏辉， 高 闯

(西安交通大学 现代设计与转子轴承教育部重点实验室，西安 710049)

为解决传统滚动轴承故障诊断及状态监测中依赖单一故障特征频率，以及诊断过程中人为主观因素造成诊断结果的不定性与效率低等问题，以包络谱与共振解调技术为例，提出一种自动识别滚动轴承故障特征频率及其倍频与调制频率的方法。该方法对信号进行包络谱或共振解调分析，在此基础上通过迭代算法依次找出转频与故障频率成分,并依据各成分在识别结果中的比例来进行故障诊断。人为仿真故障及滚动轴承加速寿命实验证明了文章方法的有效性。

故障诊断；频率识别；包络谱；智能算法

目前，随着工业4.0和大数据的相继提出，机械行业的智能化发展逐渐加快了步伐。而轴承作为机械系统的关键零部件之一，其运行状态好坏直接影响设备的正常运行。因此，轴承运行状态的监测是工业领域持续关注的焦点之一。

滚动轴承故障诊断的常用方法根据监测与诊断所采用的状态量可以分为温度法、油样分析法和振动(噪声)法[1]。温度法具有一定的局限性，且对故障不敏感；油样分析法只适用与于油润滑轴承，易受到其它颗粒的干扰，且多数情况下只适合于离线分析。而振动法因其具有的分析直观、适用范围广、结果可靠、便于发现微小故障等优点，被广泛使用。

振动是轴承自身动力学特性的外在表现，利用振动信号，可以反映轴承运转过程中状态的变化。振动信号主要由加工与安装误差引起的自身振动及外部激励引起的轴承部件的某些固定频率的振动两部分组成[2]。因此，我们可以根据轴承的振动来评判轴承的状态。

其中，包络谱分析是非常重要的一种方法。一般的包络谱分析可以得出隐藏在信号中的状态信息，在此基础上发展起来的共振解调技术也被广泛认可。它通过带通滤波、包络解调等一系列过程，可以将微弱的冲击脉冲信号从高频频带中提取出来，适合诊断早期故障。但该方法中，滤波器参数设置需要具有丰富的经验，这也造成了诊断结果具有偶然性和局限性等缺陷，给其应用带来了不便[3-4]。后来学者在其基础上提出了谱峭度[5]的概念，并用“快速峭度图”法来解决共振解调中滤波器参数选取依赖人为经验的问题[6]。

然而，以上两种方法，均依赖寻找故障特征频率来判断故障。而故障特征频率的计算只是经验公式，真实的故障特征频率与其计算值之间往往存在一定的偏差，并且即使最终找到故障特征频率，其单一性仍使故障诊断结果的说服力大打折扣。传统的依靠肉眼来寻找故障特征频率的方法，在轴承状态的实时监测中并不适用。

为解决上述问题，从而提高诊断方法的准确性及可信度。本文提出了一种滚动轴承故障频率智能识别算法，首先对信号进行包络谱或共振解调或其它有效的信号处理方法来进行分析，然后用计算机识别谱图中含有的故障频率成分，最后通过故障频率成分所占的概率比例，依据投票表决法来判断诊断结果。本文用多种故障类型分析了方法的有效性，实验结果表明该算法具有一定的工程实用价值。

1 基本方法介绍

1.1 故障特征频率

滚动轴承由内圈、外圈、滚动体和保持架四部分组成。而描述滚动轴承运动特性的量有五个，分别对应一个频率[7],即转频Fr、内圈频率Fi、外圈频率Fo、滚动体频率Fb、保持架频率Fc。由滚动轴承元件的线速度及尺寸等参数可推导出各个故障特征频率，分别为[8]

(1)

(2)

(3)

(4)

式中:Nb为滚动体的个数；Db为滚动体的直径；Dc为节圆直径；θ为接触角。实际中，由于滚动轴承的尺寸参数误差、变形等因素的存在，使实际的故障特征频率与理论的故障特征频率存在误差。

滚动轴承某部位出现损伤后，其它元器件会在运行中对损伤部位产生冲击，这种冲击信号的频率通常较低。较低的故障频率会与原来的信号进行调制，从而形成故障信号。此时需要一定的信号处理方法来获得故障频率，本文以包络谱技术与共振解调技术为例，来说明所提出的算法如何识别故障频率成分。

1.2 Hilbert解调与包络谱

Hilbert变换是一种处理带通信号的包络解调工具，可得到信号相位及瞬时频率，继而实现对故障信号的解调及故障频率的提取[9]。

设一窄带调制信号

x(t)=a(t)cos(2πf0t+φ(t))

(5)

式中，a(t)为缓慢变化的调制信号。

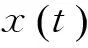
x′(t)=a(t)sin(2πf0t+φ(t))

(6)

解析信号的模或信号的包络为

(7)

解析信号的相位为

(8)

对所得的包络信号进行近一步的谱分析，即得包络谱。通过包络谱分析可得到隐藏在信号中的故障信息。

1.3 共振解调技术

在滚动轴承故障的早期阶段，由于故障冲击信号比较微弱，通过包络谱分析有时候并不能提取出故障特征频率，而该频率却可能会在高频段与共振频率发生调制现象。因此，与包络谱技术不同的是，共振解调技术可以弥补包络谱技术的某些不足，对早期故障信号进行分析。该技术首先在高频段进行带通滤波，然后通过包络解调技术将故障信号从调制信号中分离出来，继而依据故障特征频率进行故障类型判别。

2 故障频率的自动识别算法

信号进行谱分析后，谱图中所包含的信息需要进行大量计算与人工识别才能完成。对设备进行实时监测时，其工作量之大更是需计算机才可完成，并且谱图中包含的故障特征频率有与其它频率成分混叠及没显示出来的复杂情况。基于此，本文提出了故障特征频率自动识别算法，算法流程图如图1所示。

具体步骤如下：

(1) 确定待分析数据

①信号长度的确定

Ls=fs/Δf

(9)

式中:fs为采样频率;Δf为频率分辨率;为保证识别结果的可靠性，Δf取0.25,信号长度需大于等于该结果。②包络谱或共振解调分析。③选约转频30倍内的频率分量来进行识别,在此范围内基本能包含一般工况时的转频成分与故障频率成分,特殊工况时选取的范围适当调整。④需要的最大值点数n。信号的谱图中，幅值与能量有关，幅值大的频率成分不仅能反映信号的主要状态信息，而且其数量要比幅值低的随机噪声等成分少得多。依据信号谱图的这种特性，且为避免后者对故障识别的干扰，我们需要选择幅值最大的一部分点来进行分析。其数量选择的少，会漏掉许多与故障有关的频率分量；而若选择的多，则会将外界干扰等不相干的频率分量加进来，影响对故障的识别。

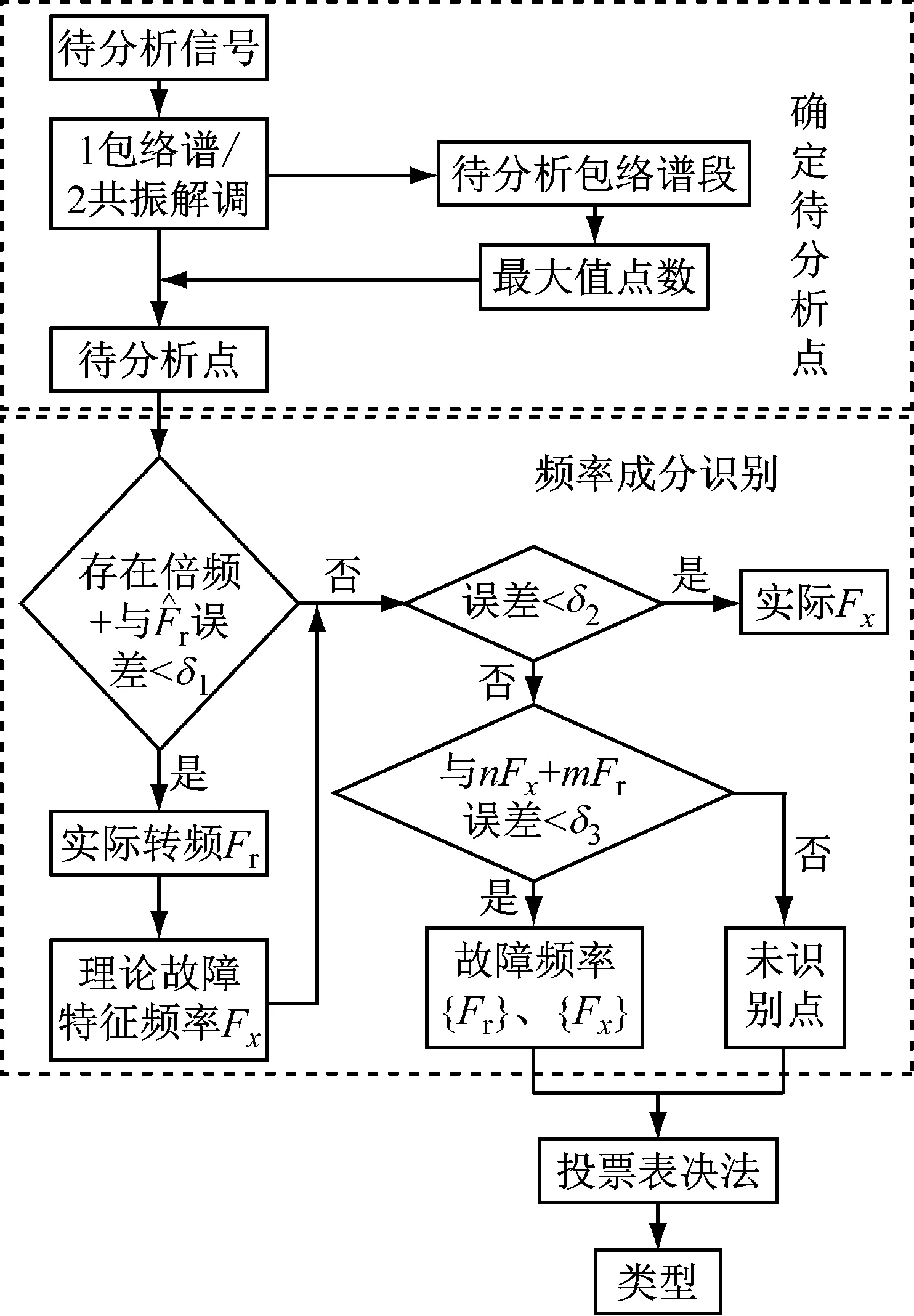
图1 算法流程图

基于此，本文从谱图中每次找5个最大的频率分量(选过之后不再选)来分析其幅值的极差。当取到合适的点数时，幅值的变化量就会衰减缓慢。以极差间的变化量小于初始极差的1/20为终止条件确定需要选择的最大值点数。

(2) 确定转频

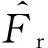
(3) 确定故障特征频率

(4) 确定相关频率

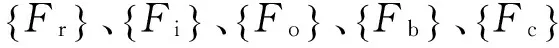
(5) 判断故障

计算并显示各故障频率成分在总点数中所占的比例，并用投票表决法来判断故障的存在与否及类型。

3 实验数据分析

3.1 仿真故障数据分析

本文用美国Case Western Reserve大学滚动轴承数据中心的实验数据[10]来分析本文方法的有效性。该实验装置主要由马达、扭矩变送器、功率计以及一些控制电路组成。实验所采用的轴承型号为：6205-2RS JEM SKF深沟球轴承，采样频率为48 K/s。故障轴承的结构参数见表1。本文所采用的故障数据是在各元件表面人为加工了一定尺寸的盲孔，实验工况及故障参数见表2。理论计算的轴承转频Fr为29.17 Hz。

表1 故障轴承的结构参数

表2 实验工况及故障特征频率

3.1.1 内圈故障识别

依上表所示，内圈故障的盲孔直径为355.6 um。若使频域信号的分辨率达到0.25，则原始信号长度至少需192 000个点。对其进行包络谱分析后，选取0～1 000 Hz频段为研究对象，进一步确定其所需的最大值点数，按上述步骤中的方法，每选5个最大值点分析其幅值变化量，结果如图2所示。

图2 每5个最大值对应的幅值变化量Fig.2 Corresponding amplitude difference of each 5 maximum values

通过阈值比较，取n=25(横坐标为5处)，即选25个最大值点来分析。又由于这25个点均存在于0～500 Hz内，因此将谱图显示至500 Hz,计算结果如图3所示。

图3 包络谱中最大的25个值

图3中标有圆圈的频率处即代表最大值点。设定δ1=1，实际转频为：Fr=29.11 Hz。从而根据特征频率与转速之比算出理论故障特征频率；设定δ2=1，找到的实际内圈故障特征频率，Fi=157.8 Hz,与计算值相差0.4 Hz左右；设定δ3=0.5，确定其故障频率与转频的倍频，识别结果见图4。

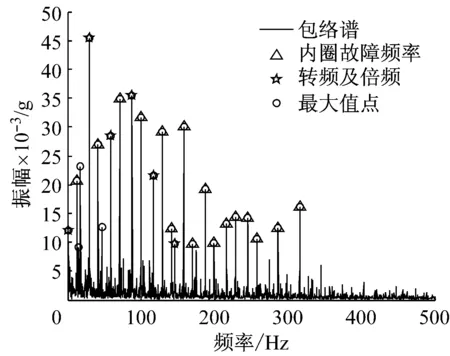
图4 内圈故障的故障识别图

由图4中可知,25个点中存在5个转频及其倍频成分；16个内圈故障频率成分；4个未识别成分。三种成分所占的比例分别为：20%、64%、16%。识别出的内圈故障频率成分较其它明显大，因此依据投票表决法可以判断存在内圈故障。

3.1.2 外圈故障识别

外圈故障数据的工况与内圈故障时相同，其盲孔直径为533.4 um。各个参数设定与内圈故障识别时相同，通过每5个点的极差计算，仍取n=25。识别出的转频仍为29.11 Hz；找到的实际外圈的故障特征频率，Fo=104.6 Hz,与计算值相差0.8 Hz左右；确定其故障频率与转频的倍频，识别结果见图5。

由图5可知,25个点中存在4个转频及其倍频成分；19个内圈故障频率成分；2个未识别成分。三种成分所占的比例分别为：16%、76%、8%。识别出的外圈故障频率成分较其它明显大，因此依据投票表决法可以判断存在外圈故障。

图5 外圈故障的故障识别图

3.1.3 识别正常信号

正常信号识别的各个参数设定与内圈故障识别时相同，通过每5个点的极差计算，取n=20。识别出的转频仍为29.11 Hz,没有找到故障频率成分，识别结果见图6。

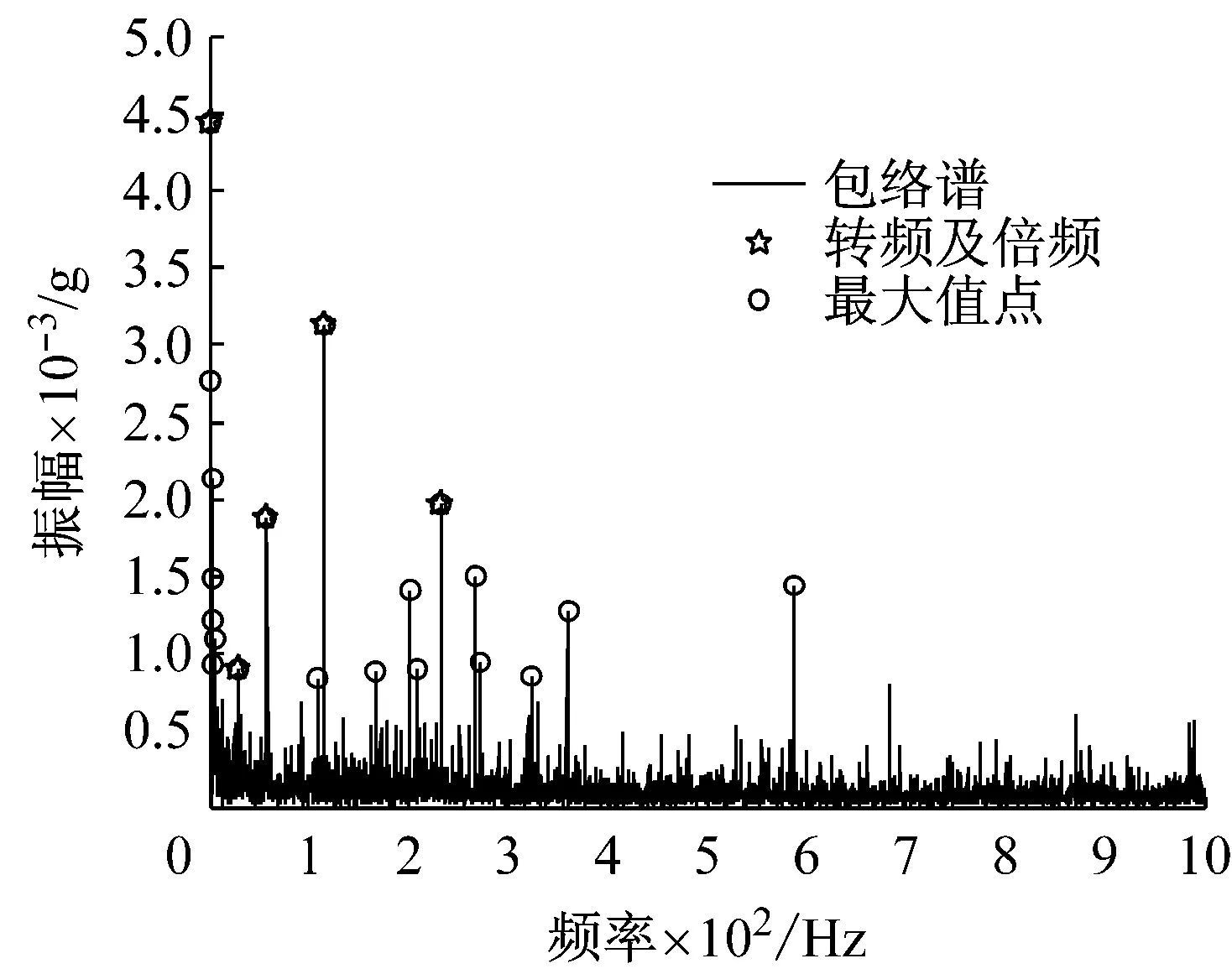
图6 正常信号识别图

由图6可知,20个点中存在4个转频及其倍频成分；16个未识别成分；两种成分所占的比例分别为：20%、80%。未识别成分明显变大，而故障成分为0，因此可以判断轴承不存在故障。

3.2 加速寿命实验数据分析

为验证该算法在实际工程应用中的效果，本文采用滚动轴承疲劳寿命加速实验获得的轴承内圈损坏后的数据[11]来进行分析。此时轴承的运转情况为开始出现明显的噪声，且不能继续使用，故障轴承见图7所示。实验所采用的轴承型号为：6309深沟球轴承，采样频率为32 K/s，采样长度为32 768，所加的轴向载荷为0，径向载荷为16.17 kN。针对每个试验轴承，每隔20 min采集一组振动数据。故障轴承的结构参数见表3，实验工况及故障参数见表4。计算出的内圈故障特征频率为165.45 Hz。

图7 故障轴承图

表3 故障轴承的结构参数

Tab.3 The structure parameters of rolling bearings

轴承中径D/mm滚子直径d/mm接触角α/(°)滚子个数/列72.5017.4608

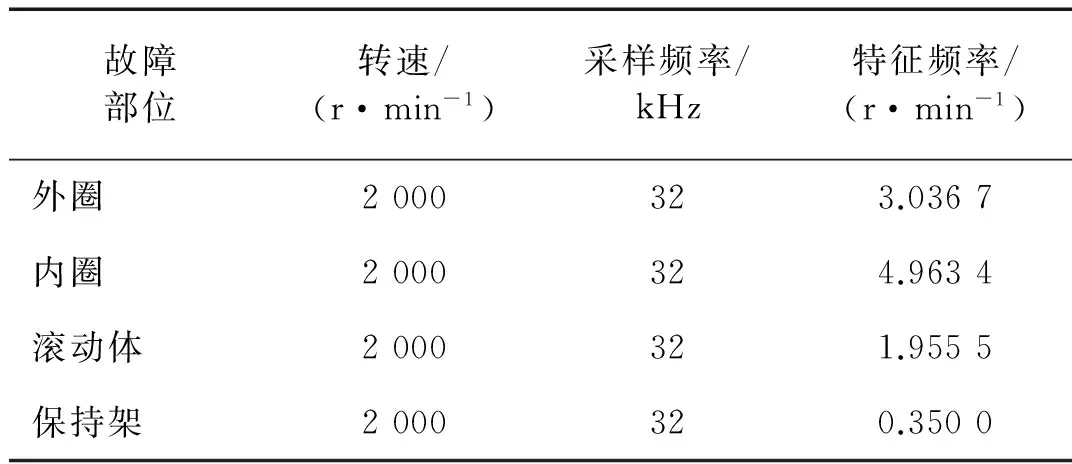
表4 实验工况及故障特征频率

由表3～表4可知，若使频域信号的频率分辨率达到0.25，则原始信号长度至少需128 000个点。为说明该方法仍适用于共振解调后的包络谱的识别，此时以共振解调后去趋势项的包络谱来作为识别对象。共振解调的快速峭度图见图8。

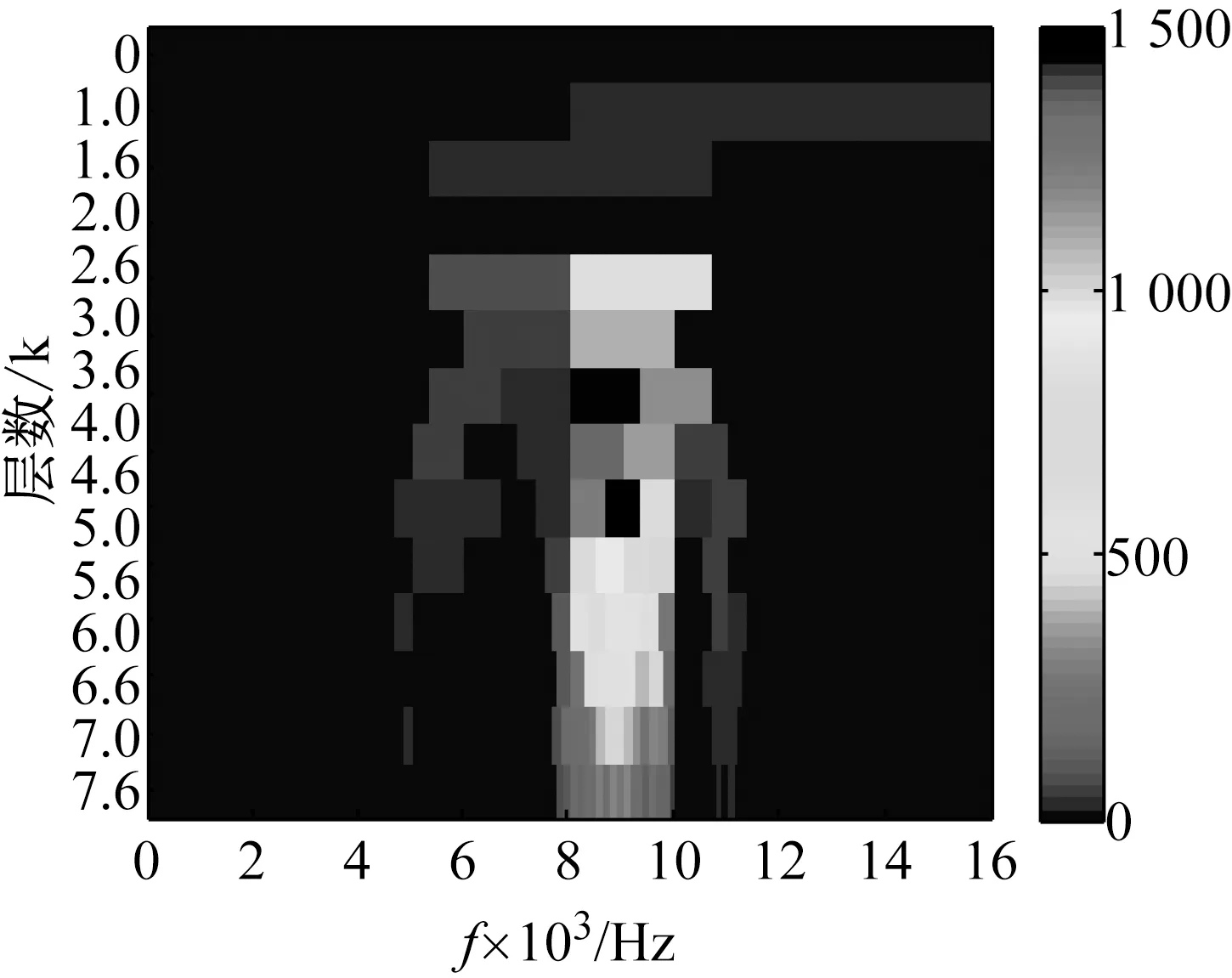
图8 信号的快速峭度图

由图8可知，谱峭度的最大值为1 500，自动确定的中心频率(共振频率)为9 000 Hz,带宽为666.7 Hz。以此作为滤波器参数，对信号滤波后做包络谱分析，选取0～1 000 Hz频段为研究对象，由每5个最大值点的极差(见图9)及阈值，确定n=20。

图9 每5个最大值对应的幅值变化量

设定δ1=1，识别出的转频为：Fr=32.8 Hz。设定δ2=1，找到的实际内圈故障特征频率，Fi=162.7 Hz,与计算值相差0.1 Hz左右。设定δ3=2，确定其故障频率与转频的倍频，识别结果见图10。

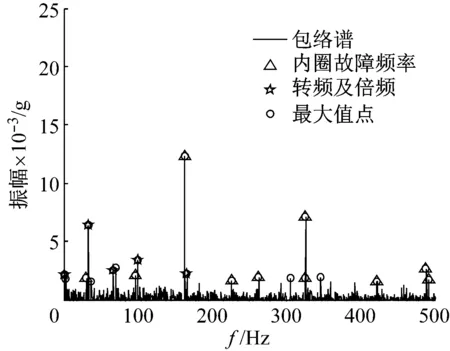
图10 内圈故障的故障识别图

在20个点中，识别出的转频相关频率成分4个，内圈故障相关频率成分10个，未识别点6个，未识别频率成分主要是实验台、传感器等实验装置及外部环境产生的频率。三种成分所占的比例分别为：20%、50%、30%。识别出的内圈故障频率成分较其它明显大，因此依据投票表决法可以判断存在内圈故障。

4 结 论

本文针对滚动轴承故障诊断的问题，以信号的包络谱技术与共振解调技术为例，提出了故障诊断与状态监测中计算机自动识别故障频率的算法，解决了工程应用中人为诊断造成的结果不定性与效率低的问题。该算法不仅适用于低频段的信号包络谱分析、早期故障诊断中高频段的共振解调分析，还适用于包括消噪方法在内的其它信号处理方法所获得的信号谱图。通过对Case Western Reserve大学滚动轴承仿真故障实验数据及加速寿命实验数据的分析，均识别出了相应的故障，验证了本文方法的有效性。

[1] SAHIN F, YAVUZ M C, ARNAVUT Z, et al. Fault diagnosis for airplane engines using Bayesian networks and distributed particle swarm optimization[J]. Parallel Computing, 2007, 33(2): 124-143.

[2] CHANG Yanwei, WANG Yaocai, LIU Tao, et al. Fault diagnosis of a mine hoist using PCA and SVM techniques[J]. Journal of China University of Mining and Technology, 2008, 18(3): 327-331.

[3] MCFADDEN P D, SMITH J D. Vibration monitoring of rolling element bearing by the high-frequency esonance technique-a review[J]. Tribology International, 1984, 17(1): 3-10．

[4] 王宏超，陈进，董广明，等. 基于快速kurtogram算法的共振解调方法在滚动轴承故障特征提取中的应用[J]. 振动与冲击，2013, 32(1):35-38.

WANG Hongchao, CHEN Jin, DONG Guangming,et al. Application of resonance demodulation in rolling bearing fault feature extraction based on fast computation of kutrogram[J]. Journal of Vibration and Shock,2013,32(1): 35-38.

[5] DWYER R F. Detection of non-gaussian signals by frequency domain kurtosis estima-tion[C]//Acoustic, Speech and Signal Processing. Boston: IEEE International Conference on ICASSP, 1983: 607-610.

[6] ANTONI J. Fast computation of the kurtogram for the detection of transient faults[J]. Mechanical Systems and Signal Processing,2007,21(1):108-124.

[7] LI B, CHOW M Y, TIPSUWAN Y, et al. Neural-network-based motor rolling bearing fault diagnosis[J]. IEEE Transaction on Indusrial Electronics,2000,47(5): 1060-1068.

[8] TANDON N, CHOUDHURY A. A review of vibration and acoustic measurement methods for the detection of defects in rolling element bearing[J]. Tribology International,1999,32(8):469-480.

[9] 何正嘉, 訾艳阳,张西宁, 等. 现代信号处理及工程应用[M]. 西安：西安交通大学出版社, 2007.

[10] LOPARO K A. Bearing vibration data set[Z]. Case Western Reserve University. http: ∥www． eecs． cwru． edu /laboratory /bearing /welcome _overview． htm．

[11] ZHU Xiaoran, ZHANG Youyun, ZHU Yongsheng. Bearing performance degradation assessment based on the rough support vector data description[J]. Mechanical Systems and Signal Processing, 2013, 34(1/2): 203-217.

An automatic recognition method for characteristic frequency of rolling bearings

GAO Dawei, ZHU Yongsheng, LIU Yuwei, CAO Penghui, GAO Chuang

(Key Laboratory of Education Ministry for Modern Design and Rotor-Bearing System, Xi’an Jiaotong University, Xi’an 710049, China)

In order to solve problems, such as, overdependence on single fault characteristic frequency, and the ambiguity and inefficiency of diagnosis results caused by subjective factors in fault diagnosis of rolling bearings, a method using the envelope spectrum and resonance demodulation analysis of signals was proposed to identify the fault characteristic frequency, and its multiplications and modulation frequency components of rolling bearings. Firstly, the original signal was analyzed with the envelope spectrum or resonance demodulation analysis. Then, a specific algorithm was used to identify faulty frequency components and rotating frequency in the spectrum. At last, the fault diagnosis of rolling bearings was conducted with the corresponding proportions of the identified frequency components. The fault diagnosis simulations and the life acceleration tests of rolling bearings demonstrated the validity of the proposed method．

fault diagnosis; frequency identification; envelope spectrum; intelligent algorithm

国家自然科学基金资助项目(51275383)

2016-01-07 修改稿收到日期：2016-03-16

高大为 男，硕士生，1992年3月生

朱永生 男，教授,1973年9月生

TH212；TH213.3

A

10.13465/j.cnki.jvs.2017.09.009