二维声学黑洞对弯曲波的能量聚集效应

黄 薇， 季宏丽,， 裘进浩， 成 利

(1. 南京航空航天大学 机械结构力学及控制国家重点实验室，南京 210016； 2.香港理工大学 机械工程系，香港 999077)

二维声学黑洞对弯曲波的能量聚集效应

黄 薇1， 季宏丽1,2， 裘进浩1， 成 利2

(1. 南京航空航天大学 机械结构力学及控制国家重点实验室，南京 210016； 2.香港理工大学 机械工程系，香港 999077)

声学黑洞(Acoustic Black Holes,ABH)效应是利用结构厚度以一定幂函数形式减小，致使弯曲波的相速度逐渐减小而实现能量逐渐聚集，理想情况下弯曲波波速减小为0从而无法传递到结构边缘，也就不会发生反射。声学黑洞效应使得结构产生高能量密度区域，因此能高效应用于能量回收和振动噪声控制。为了研究二维声学黑洞结构具有弯曲波能量聚集效应，运用有限元分析软件ABAQUS建立了二维声学黑洞模型，从时域上研究弯曲波在声学黑洞区域的传播过程，结合有限元数值结果与振动功率流的结果分析弯曲波能量聚集过程。最后通过激光超声实验系统对二维声学黑洞中弯曲波传播过程进行成像与分析，实验结果验证了二维声学黑洞结构对弯曲波能量的聚集效应。

声学黑洞；弯曲波；有限元分析；能量聚集；功率流

声学黑洞(Acoustic Black Holes,ABH)将物理学中的黑洞概念引入到波动和声振领域中，并将其作为一种全新的概念提出。声学黑洞效应通过结构阻抗的变化，致使结构中波的相速度和群速度发生变化，在结构局部区域实现波的聚集。薄板结构中，如果阻抗的变化通过板的厚度以一定指数形式变化来实现，弯曲波速会随着厚度的减小逐渐减小，在理想的情况下波速减小为0，这样就不会在尖端产生反射[1-2]。Georgiev等[3]运用Runge-Kutta-Fehlberg数值方法计算了频域内的阻抗矩阵，并得到了反射系数矩阵。Conlon等[4]运用有限元和边界元的数值方法，从频域上研究了排布多个声学黑洞的板结构的声辐射特性。Bayod等[5-8]针对含有ABH的梁和板结构进行实验观察和分析，实验结果表明声学黑洞效应的有效频率作用主要集中于中高频。尽管现有研究从频域上表明了声学黑洞效应的存在，但是波在声学黑洞结构中的传播过程无法通过频域方法得到很好的解释，无法从时域上认识声学黑洞结构中的波传播过程和黑洞效应形成的机制。

此外，声学黑洞结构由于实际加工工艺问题往往产生截断，研究发现很小的截断厚度就会对黑洞效应产生严重的影响，声学黑洞结构边缘的反射系数可达到50%～70%[9]。Bayod等研究了声学黑洞边缘的制造方法，通过直接在等厚度均匀板上拉延出一段尖锐的边缘从而在一定程度上克服声学黑洞边缘制造的困难。将薄板结构的厚度按照一定的形式裁剪即可得到二维声学黑洞结构。理想二维声学黑洞使得入射到黑洞的弯曲波被吸入声学黑洞的中心[10]。实际二维声学黑洞也会由于中心厚度极薄而产生截断等缺陷，因此容易在中心处形成圆形穿孔。Conlon等通过数值表明了缩小声学黑洞中心孔径，在一定频率范围内能够大大提高声学黑洞效应。Bowyer等[11-12]将圆形压痕置于矩形板中并进行了相关的实验研究，表明中心圆孔的存在会对声学黑洞效应产生影响。现有的对声学黑洞的研究着重于在频域特性上研究非理想黑洞效应的存在，而缺乏有效的手段揭示波在声学黑洞中的传播过程以及截断大小等参数对声学黑洞效应的影响关系。

本文针对这些问题，以中心处为圆形平台的二维声学黑洞结构为研究对象，从时域上研究声学黑洞结构中弯曲波的传播。对含有二维声学黑洞的板结构建立有限元数值模型，并采用有限元数值计算结果进行振动功率流分析，解释了弯曲波能量在声学黑洞中的传播过程与弯曲波的能量聚集效应，并探究了声学黑洞中心圆形平台大小对弯曲波传播的影响。最后通过基于激光超声技术的实验方法验证了声学黑洞结构对弯曲波能量的聚集效应。

1 声学黑洞结构中的弯曲波

在一维厚度变化的均匀介质中，弯曲波动方程为

(1)

U(x)=A(x)eiΦ(x)

(2)

其中，

(3)

(4)

式中:Φ为累积相位;kp=ω/cp，kp为均匀板的波数。对于一个厚度呈指数形式变化的结构

h(x)=εxm

(5)

当指数m≥2，累积相位Φ将趋于无限大，也就是说波无法到达边界也无法反射回来，因此弯曲波在边缘处被捕获而能量聚集。

对于变厚度的薄板结构，其弯曲波动方程为

(6)

假设不考虑结构的转动惯量与剪切效应，波数k为

k=(ρhω2/D)1/4

(7)

式中,ω为角频率，根据c=ω/k可得到弯曲波相速度

(8)

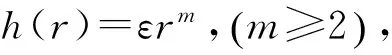
2 模型的建立

2.1 二维声学黑洞

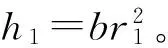
(9)

(a)二维声学黑洞板与横截面(b)横截面厚度变化示意图

图1 二维声学黑洞示意图

Fig.1 Schematic of two-dimensional ABH

2.2 有限元模型

为了研究弯曲波在声学黑洞结构中的传播特性，在有限元软件ABAQUS中建立了含有二维声学黑洞的板结构模型(350 mm×240 mm×5 mm)，如图2所示。为研究中心平台大小即截断大小对二维声学黑洞结构中弯曲波聚集的影响，分别对r1=20 mm和r1=30 mm的ABH建立有限元模型进行计算。在计算中所使用的其他参数如表1所示。二维声学黑洞局部区域网格的划分如图3所示，采用平面应力下的C3D8R单元求解，每个波长内至少包含10个单元以保证计算精度。

图2 含有二维声学黑洞的板结构有限元模型

表1 结构材料与几何参数表

Tab.1 Geometrical and material properties of the plate

参数数值弹性模量/GPa270板材料密度/(kg·m-3)7800泊松比0.3m2h2/mm5r2/mm100

图3 含有二维声学黑洞板结构局部区域网格的划分

结构受到五周期猝发音的集中力激励，激励点距离声学黑洞中心点150 mm。如图4所示，激励中心频率为f=20 kHz。结构左端边界固支，有限元求解得到结构位移与速度响应，运用Python语言后处理获取二维声学黑洞板结构平面板一侧结点响应，以Matlab平台编程分析振动功率流以及能量分布。

(a)五周期猝发音激励幅值

(b)激励施加位置示意

3 振动功率流分析

板上任一点的振动功率流为x方向和y方向的振动功率流分量的矢量和

(10)

时间平均的功率流为

(11)

式中:F为力;v为速度。功率流在某一方向的分量由剪力、弯矩和扭矩三部分组成。例如沿x轴分量经过简化可写成

(12)

现由两点之间的速度信号求得某方向上的功率流，对于简谐波

(13)

代入式(12)，于是有

(14)

假设结构上沿x方向临近两点间距为d′如图5,速度分别为v1和v2，则中点速度近似为

(15)

于是有

(16)

根据维纳-辛钦公式,信号的互相关函数与互功率谱函数互为傅里叶变换对

(17)

(18)

式中,V1和V2分别为v1和v2的傅里叶变换形式，按照帕斯瓦尔定理,信号按时域计算的平均功率等于按频域计算的平均功率,可以得到功率流在频域的表达式(取实部表示有功功率)

(19)

(20)

代入式(19)，就可得到功率流在x方向分量的互谱表达式(y方向可用同样方法求得)

(21)

图5 两点排布坐标示意图

4 有限元数值计算结果

图6为有限元数值计算所得位移响应，选取板中含有二维声学黑洞的正方形区域(240 mm×240 mm)部分进行讨论，声学黑洞位于此正方形区域的中央位置，图6(a)与图6(b)为r1=20 mm的声学黑洞，图6(c)与图6(d)为r1=30 mm的声学黑洞，图6(a)与图6(c)为t=0.1 ms时的位移场，图6(c)与图6(d)为t=0.3 ms时的位移场。可见，在点激励下弯曲波传播以散射状入射于声学黑洞，而后在声学黑洞中发生弯曲而能量聚集，并且波长在黑洞中心区域被压缩，波动幅值显著增大，在声学黑洞中形成高能量密度区域。增大中心圆板的半径，截断厚度也相应增大，使得聚集在中心的弯曲波幅值降低，聚集区域明显随着平台半径的增大而扩散。

(22)

式中,∑表示对0到T时刻内的数值求和，图7为t=0.3ms内的能量分布，图7(a)为r1=20mm的声学黑洞，图7(b)为r1=30mm的声学黑洞。明显可以看出能量聚集于声学黑洞中，声学黑洞对结构中的弯曲波产生了类似陷波器的效果。同样可以看出当声学黑洞中心的圆形平台扩大，能量聚集的范围扩大，但是依然聚集在声学黑洞的中央区域。因此，减小中心平台的大小即减小截断厚度，声学黑洞的能量聚集效果增强。

振动功率流分析可以更加直观地体现弯曲波能量在声学黑洞中的传递。采用第3节中的方法计算二维声学黑洞板中的振动功率流如图8所示，图8(a)与图8(b)为r1=20mm的声学黑洞，图8(c)与图8(d)为r1=30mm的声学黑洞，图8(b)与图8(d)为图8(a)与图8(c)的局部放大。显而易见，功率流以散射状入射于声学黑洞区域并在黑洞非均匀区域发生偏转而聚集于声学黑洞中心。对比图8(b)与图8(d)，当中心平台减小，在平台附近的功率流矢量偏转增大，因此，能量能够更加高效地聚集于声学黑洞中心。

5 实验验证

声学黑洞试件在实验中的扫描区域与AE传感器的位置如图10所示，扫描区域大小为220mm×220mm，在宽度方向上距离边界10 mm，声学黑洞中心距离板长度方向边界130 mm。ABH位于扫描区域中央。AE传感器位于结构对称轴上与声学黑洞中心的距离为d=150 mm。

(a)

(b)

(c)

(d)

(a) 为r1=20 mm的声学黑洞

(b) 为r1=30 mm的声学黑洞

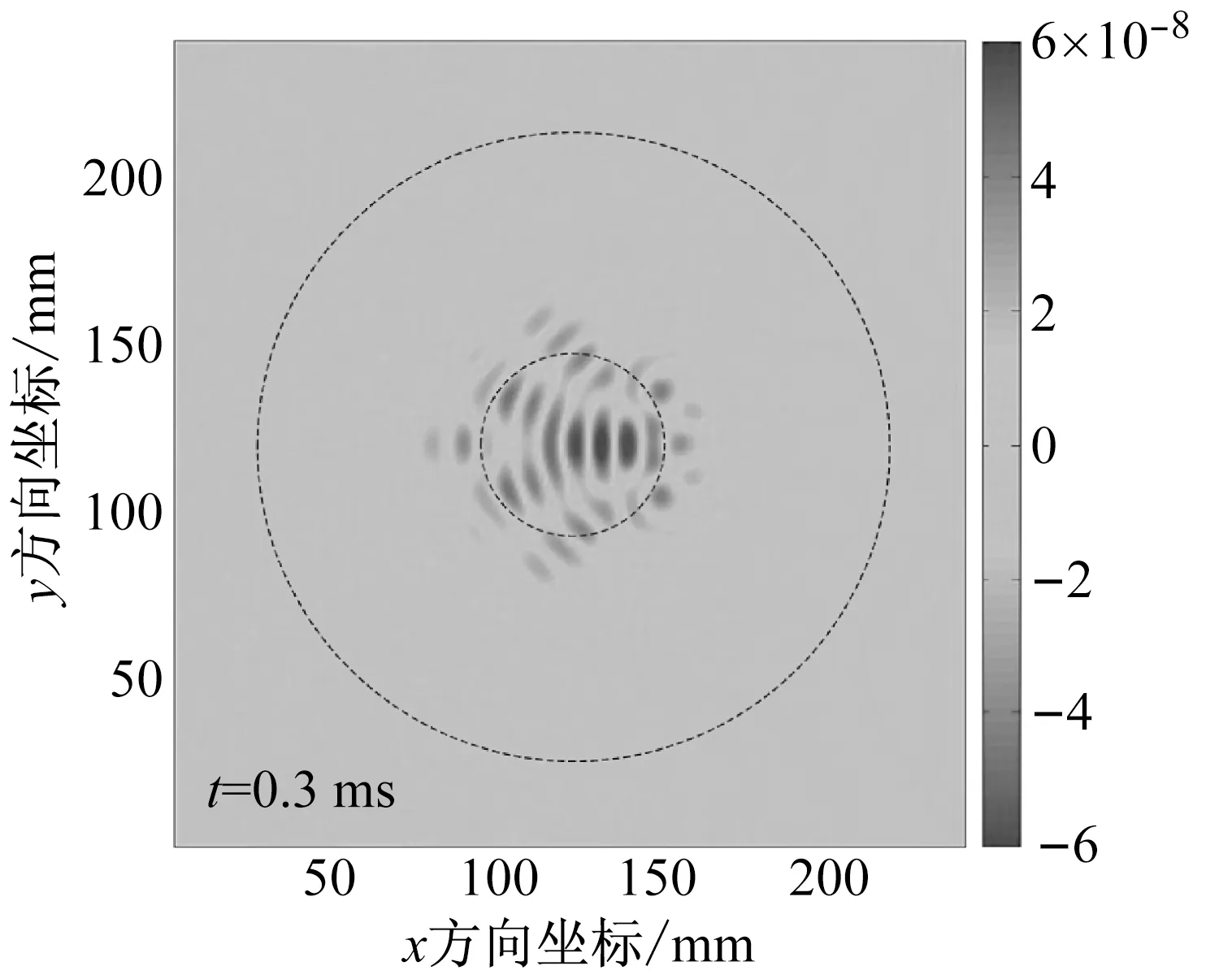
实验采样频率为1 MHz，采样时间为0.4 ms，x方向与y方向的空间采样间隔为1 mm。对采集得到的信号经过15～25 kHz的滤波处理后，得到不同时刻波场图像，图11为0.3 ms时刻波场图像。结果显示了弯曲波在声学黑洞板中聚集于声学黑洞中心区域。

将AE所采集到的信号运用式(22)的方法计算能量在声学黑洞板上的分布，如图12，可见在声学黑洞的中央区域，能量明显聚集。将实验所得的结果(图11和图12)与仿真所得结果(图6和图7)进行对比，实验与仿真基本吻合。图13为通过实验所采集的信号计算能量功率流分布，同样可以看出能量传递到声学黑洞，在中心圆板附近功率流矢量偏转而能量聚集于黑洞中。

(a)

(b)

(c)

(d)

(a) 实验系统示意图

(b) 实验系统实物图

图10 扫描区域与AE传感器的位置

6 结 论

本文利用有限元数值计算以及基于激光超声技术的实验方法对含有中心圆形平台的二维声学黑洞结构的弯曲波能量聚集效应进行研究，结合数值计算结果与振动功率流分析，从时域上研究了弯曲波在声学黑洞结构中聚集的现象与能量聚集过程，从功率流传递路径图中可以直观地看出弯曲波射线的偏转，弯曲波能量聚集在声学黑洞的中心区域。并研究了不同圆形平台的大小对弯曲波能量聚集效应的影响，减小中心平台可提高声学黑洞的能量聚集效应。此外，通过激光超声技术实验验证了弯曲波在声学黑洞板中的聚集。本文的研究对后续振动噪声控制及能量回收的应用具有指导意义。

图11 二维声学黑洞板0.3 ms时刻波场图像

Fig.11 Experimental results of wavefields for plate with two-dimensional ABH at 0.3 ms

图12 实验中二维声学黑洞板0.3 ms内的能量分布

Fig.12 Experimental results of energy distribution for plate with two-dimensional ABH within 0.3 ms

(a)二维声学黑洞板中功率流分布

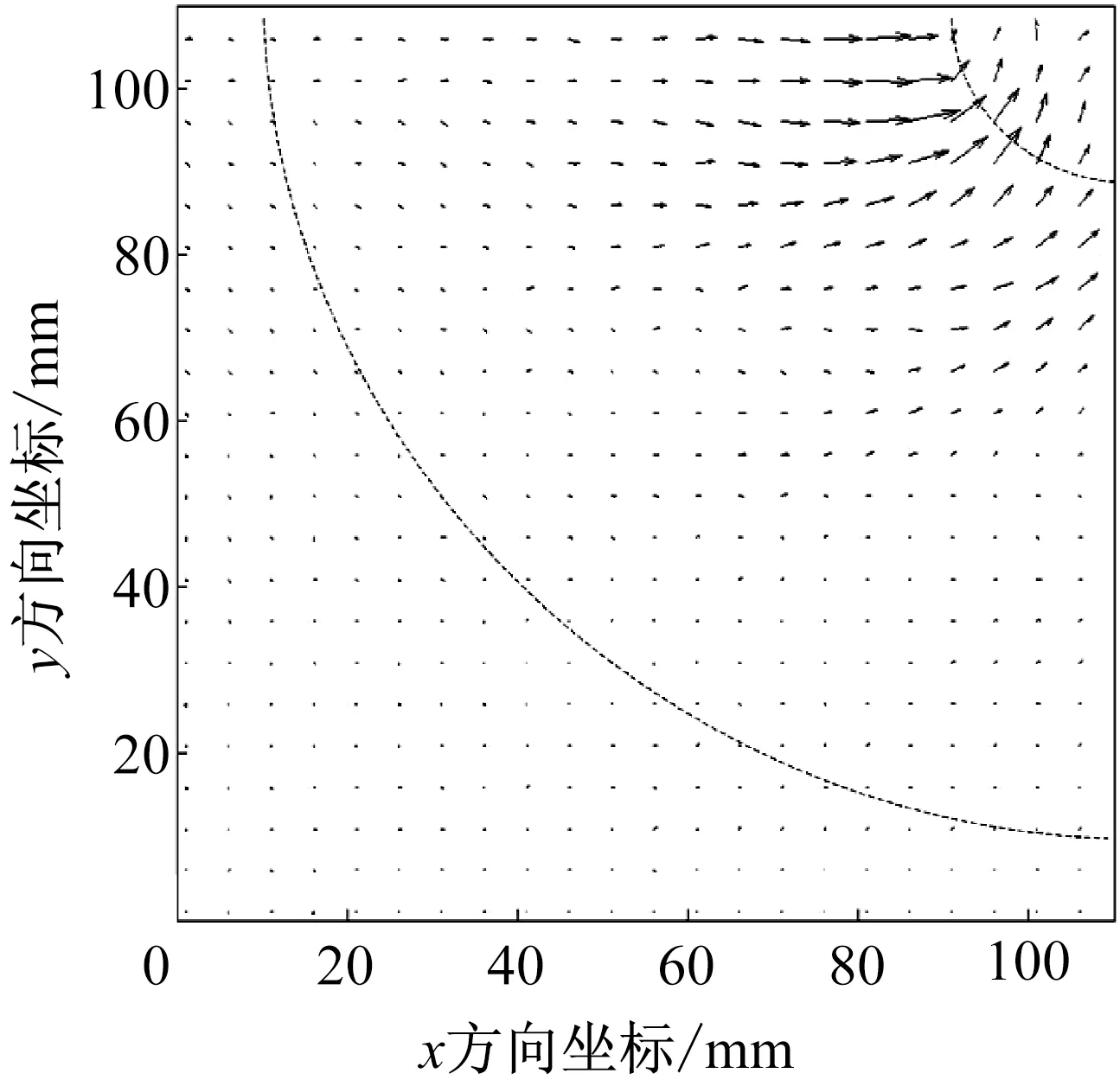
(b)四分之一板的放大图

[1] KRYLOV V V, SHUVALOV A L. Propagation of localised flexural vibrations along plate edges described by a power law[J]. Institute of Acoustics, 2000, 22:263-270.

[2] KRYLOV V V, TILMAN F J B S. Acoustic ‘black holes’ for flexural waves as effective vibration dampers[J]. Journal of Sound & Vibration, 2004, 274(3/4/5):605-619.

[3] GEORGIEV V B, CUENCA J, GAUTIER F, et al. Damping of structural vibrations in beams and elliptical plates using the acoustic black hole effect[J]. Journal of Sound & Vibration, 2011, 330(11):2497-2508.

[4] CONLON S C, FAHNLINE J B, FABIO S. Numerical analysis of the vibroacoustic properties of plates with embedded grids of acoustic black holes[J]. Journal of the Acoustical Society of America, 2015, 137(1):447-447.

[5] BAYOD J J. Experimental study of vibration damping in a modified elastic wedge of power-law profile[J]. Journal of Vibration & Acoustics, 2011, 133(6):1754-1754.

[6] BOWYER E P, O′BOY D J, KRYLOV V V, et al. Experimental investigation of damping flexural vibrations using two-dimensional acoustic ‘black holes’[D]. Belgium: Katholieke Universiteit Leuven, 2010.

[7] O’BOY D J, KRYLOV V V, KRALOVIC V. Damping of flexural vibrations in rectangular plates using the acoustic black hole effect[J]. Journal of Sound & Vibration, 2010, 329(22):4672-4688.

[8] BOWYER E P, O’BOY D J, KRYLOV V V, et al. Effect of geometrical and material imperfections on damping flexural vibrations in plates with attached wedges of power law profile[J]. Applied Acoustics, 2012, 73(5):514-523.

[9] KRYLOV V V, SHUVALOV A L. Propagation of localised flexural vibrations along plate edges described by a power law[J]. Institute of Acoustics, 2000, 22:263-270.

[10] KRYLOV V V. Propagation of plate bending waves in the vicinity of one- and two-dimensional acoustic black holes[C]//Proceedings of the First International ECCOMAS Thematic Conference on Computational Methods in Structural Dynamics and Earthquake Engineering. Grete: [s.n.], 2007.

[11] BOWYER E P, LISTER J M, KRYLOV V V, et al. Experimental study of damping flexural vibrations in tapered turbofan blades[C]//Proceedings of the Acoustics 2012 Nantes Conference. Nantes: [s.n.], 2012:395-396.

[12] BOWYER E P, O’BOY D J, KRYLOV V V, et al. Experimental investigation of damping flexural vibrations in plates containing tapered indentations of power-law profile[J]. Applied Acoustics, 2013, 74(4):553-560.

[13] ZHANG C, QIU J, JI H. Laser ultrasonic imaging for impact damage visualization in composite structure[C]//EWSHM-7th European Workshop on Structural Health Monitoring. Nantes:[s.n.], 2014:2199-2205.

[14] ZHANG C, JI H, QIU J, et al. Research on interference energy calculation method in laser ultrasonic technique[J]. Acta Optica Sinica, 2014, 34(7):714001.

[15] WU Y, QIU J, ZHANG C, et al. A method to improve the visibility of the damage-reflected wave[J]. Chinese Journal of Lasers, 2014, 41(3):0308001.

Energy focusing effect of Two-dimensional acoustic black hole on flexural waves

HUANG Wei1, JI Hongli1,2, QIU Jinhao1, CHENG Li2

(1. State Key Laboratory of Mechanics and Control of Mechanical Structures, Nanjing University of Aeronautics & Astronautics, Nanjing 210016， China； 2. Department of Mechanical Engineering, Hong Kong Polytechnic University, Hong Kong 999077, China)

The acoustic black hole (ABH) phenomenon in thin-walled structures with a power function form reducing leads to a smooth reduction of the phase velocity of flexural waves and energy focalization. In an ideal case, flexural wave velocity decreases to zero so that it never reaches a structure’s edge, much less reflects back. This causes structural areas with high energy density, the high energy effects can be used for various engineering applications, such as, energy harvesting, vibration and noise control and so on. In order to investigate the energy focusing effect of two-dimensional acoustic black hole on flexural waves, the model of two-dimensional acoustic black hole was built using the finite element software ABAQUS, and numerical simulations were conducted for the transmission of flexural wave in the acoustic black hole areas. Vibration power flow and finite element simulation were combined to analyze the energy focalization of flexural waves. Finally, the transmission process of flexural wave in two-dimensional acoustic black hole was imaged and analyzed by using the laser ultrasonic scanning technique. The test results verified the energy focalization effect of two-dimensional acoustic black hole on flexural waves.

acoustic black hole; flexural wave; finite element analysis; energy focalization; power flow

国家自然科学基金重点项目(11532006);机械结构力学及控制国家重点实验室(南京航空航天大学)自主研究课题资助(0515Y02);中央高校基本科研业务费专项资金资助(NE2015101);六大人才高峰C类(JXQC-002)；江苏高校优势学科建设工程资助项目;江苏省重点基金项目(BK20150061)

2015-12-17 修改稿收到日期：2016-03-15

黄薇 女，博士生，1991年生

季宏丽 女，副教授，1983年生

O421+．5

A

10.13465/j.cnki.jvs.2017.09.008