基于时间-小波能量谱样本熵的滚动轴承智能诊断方法

邓飞跃, 唐贵基

(1.石家庄铁道大学 机械工程学院，石家庄 050043； 2.华北电力大学 能源动力与机械工程学院，河北 保定 071003)

基于时间-小波能量谱样本熵的滚动轴承智能诊断方法

邓飞跃1, 唐贵基2

(1.石家庄铁道大学 机械工程学院，石家庄 050043； 2.华北电力大学 能源动力与机械工程学院，河北 保定 071003)

为了解决滚动轴承故障模式智能识别与运行状态检测问题，提出了时间-小波能量谱样本熵的计算方法，并将其作为特征参数用于滚动轴承智能诊断的研究。采用Hermitian小波对轴承信号进行连续小波变换，得到蕴含故障信息的时间-小波能量谱序列，再通过计算其样本熵值，量化提取信号中的故障特征信息。轴承不同故障模式下的时间-小波能量谱样本熵区分明显，以此作为特征向量输入支持向量机，实现了对轴承不同故障模式的智能识别。之后计算轴承全寿命周期实验数据的时间-小波能量谱样本熵，按照时间顺序排列，绘制出了轴承运行状态曲线，通过判断曲线走势可有效诊断出轴承早期故障的发生。实验结果表明，时间-小波能量谱样本熵可以有效用于滚动轴承智能诊断的研究。

滚动轴承；智能诊断；连续小波变换；样本熵；支持向量机

滚动轴承是旋转机械中支承转动轴的核心部件，对于保持转轴的工作位置和旋转精度具有至关重要的作用，同时它也是机械设备中最易发生故障损坏的部件之一[1]。随着计算机技术的不断发展，采用基于信号处理技术结合人工智能诊断方法对滚动轴承故障进行智能诊断已经越来越广泛。

采用人工智能方法对滚动轴承故障进行诊断，需要在轴承信号中准确提取出表征故障信息的特征参数，这一过程对于轴承智能诊断尤为关键。近年来，各种熵的理论被广泛用于轴承故障特征参数的提取中，王小玲等[2]采用短时傅里叶变换(Short-time Fourier Transform，STFT)方法得到了信号的幅值谱，通过计算Shannon熵，提出了以频带熵为特征参数用于轴承故障识别；赵志宏等[3]利用EEMD方法对振动信号进行分解，计算前几个内蕴模式分量的样本熵(Sample Entropy, SampEn)作为输入支持向量机(Support Vector Machine, SVM)的特征向量，完成了对轴承故障类型的智能识别；赵志宏等[4]对轴承信号进行小波包分解，通过计算各个子信号的样本熵作为特征向量输入SVM实现了对轴承故障模式的识别；冯辅周等[5]通过小波相关滤波技术对轴承信号进行降噪处理，然后分析信号排列熵的变化趋势，对轴承运行状态进行了有效检测。上述方法都取得了不错的效果，但这些方法得到的特征参数只能用于滚动轴承智能诊断过程中单一目标的研究，鲜有能同时用于轴承故障模式智能识别与运行状态检测的分析方法。

Hermitian小波具有较强的信号奇异性检测和瞬时相位识别能力，因此本文选用Hermitian小波通过连续小波变换得到了蕴含轴承故障信息的时间-小波能量谱，再结合样本熵理论，计算时间-小波能量谱样本熵作为轴承故障模式识别和运行状态检测的特征参数。通过SVM智能分类识别和轴承运行状态趋势判断，较为准确地实现了滚动轴承的故障模式识别和运行状态检测。

1 基于Hermitian连续小波变换的时间-小波能量谱样本熵

1.1 Hermitian小波

(1)

(2)

Hermitian小波的时域表达式为

(3)

Hermitian小波的时域波形如图1所示。从图中可知:该小波的实部为偶函数，是传统的MexicoHat小波，在支撑区域内共振荡1.5次；虚部为奇函数，在支撑区域内振荡1次，根据Nyquist采样定理，仅需很少的采样点就能准确描述Hermitian小波的波形[8]。小波变换可看作是对信号的卷积滤波，滤波器的点数越多平滑掉信号中奇异点的机率也就越大，而信号中的奇异点是反映重要故障信息的载体，因此Hermitian小波具备较强的奇异性检测能力，更有利于轴承信号中特征信息的提取。

图1 Hermitian小波波形

另外，通过傅里叶变换，Hermitian小波的频谱表达式为

(4)

式中，ω为角频率。由式(4)可知，Hermitian小波傅里叶变换的结果为实数，因此Hermitian小波变换可以做到无相位移动，对信号进行卷积滤波时不会改变原始的相位信息。

1.2 时间-小波能量谱

设φ(t)是一有限能量函数，φ(t)∈L2(R)，傅里叶变换后φ(ω)满足如下的容许条件

(5)

式中,φ(t)为母小波，对φ(t)进行伸缩和平移变换，尺度参数和位置参数分别设为a和b，则得到一组函数φa,b(t)为

(6)

式中，φa,b(t)称为小波基函数。信号x(t)的连续小波变换表示为

(7)

式中，φ*(t)是φ(t)的共轭。

依据小波变换过程中能量守恒原理，可得

(8)

将式(8)改写为

(9)

令

(10)

那么E就被称为信号x(t)连续小波变换后的时间-小波能量谱[9]。

时间-小波能量谱表征的是小波变换后信号能量随时间的分布情况，当滚动轴承某个元件发生故障时，其他元件通过故障点位置就会发生冲击振动。因为冲击信号频率分布较广，在冲击发生时，在各个频率段内均有信号能量的分布，若将信号沿着尺度轴积分，可得随时间变化的信号小波能量分布。若在时间轴的某段范围内，轴承元件没有发生故障冲击，那么信号的小波能量分布就相对较为平缓，若发生了故障冲击，在该时刻的能量分布中就会出现一个峰值。因此，信号小波变换后得到的时间-小波能量谱中蕴含了故障冲击的特征信息，也就是滚动轴承的故障特征信息。

1.3 样本熵计算

样本熵是对时间序列复杂度的一种度量，熵值越小，时间序列复杂度越小，自相似性越高。它在计算概率时不包括向量的自身匹配，计算更加简单。相比Shannon熵、K熵、近似熵等方法，样本熵对数据长度的依赖更小，一致性更好，并且对于丢失数据也不敏感，抗干扰和抗噪声的能力更强。

文献[3]中给出了样本熵的详细计算过程，本文照此过程计算时间-小波能量谱序列的样本熵。需要指出的是，样本熵计算过程中需要嵌入两个参数m和r，根据文献[3-4]的研究成果：当m=1或m=2，r=(0.1～0.25)Std(Std为数据序列的标准差)时计算得到的样本熵具有较为合理的统计特性，因此本文取参数为m=2，r=0.2Std。

2 时间-小波能量谱样本熵分析

2.1 不同故障模式下的比较

滚动轴承故障模式不同，对应振动信号经过Hermitian连续小波变换后的时间-小波能量谱中蕴含的特征信息也不同，能量谱在自相似性和复杂程度上会有很大差异，计算样本熵并将其作为特征参数可用于表征轴承不同故障模式下的特征信息。

截取实际试验中轴承在正常、滚动体、内圈和外圈故障4种状态下的振动信号进行分析。实验中，转轴转速为1 470 r/min，采样频率为12 800 Hz，数据长度为8 192个点。滚动轴承4种运行模式下振动信号的时域波形如图2所示。经过Hermitian连续小波变换后，计算各自的时间-小波能量谱如图3所示。从图中可知:轴承正常运行状态下的时间-小波能量谱沿时间轴分布最为混乱，幅值也最小；滚动体故障发生时，时间-小波能量谱沿时间轴分布出现了一些峰值；内圈故障时，能量谱中峰值出现的个数较多；外圈故障时出现的峰值个数最多。

分别计算原始信号和时间-小波能量谱序列的样本熵，结果如表1所示。从表中可知，在轴承不同运行模式下，计算两类信号序列得到的样本熵值大小是不同的，但样本熵值都在轴承正常运行时最大，其次是外圈故障和内圈故障，发生滚动体故障时数值最小。这说明，轴承正常运行时信号序列的复杂程度最高，其次是发生外圈故障和内圈故障，滚动体故障运行时信号的复杂程度最小，这个顺序也和时间-小波能量谱序列中出现的峰值个数情况相一致。

(a) 正常

(b) 滚动体故障

(c) 内圈故障

(d) 外圈故障

(a) 正常

(b) 滚动体故障

(c) 内圈故障

(d) 外圈故障

表1 样本熵计算

为进一步比较两种信号序列的样本熵在轴承不同工况下的区分度情况，将表1中数据进行归一化处理，结果如表2所示。从表2中结果可知，时间-小波能量谱样本熵在轴承4种运行模式下的区分度明显，并且彼此区分程度要远好于原始信号的直接样本熵，后者在轴承发生滚动体故障和内圈故障时样本熵值大小接近，采用原始信号直接样本熵作为特征参数显然无法正确区分轴承滚动体故障和内圈故障。通过Hermitian连续小波变换得到的时间-小波能量谱序列相比原始信号蕴含了更为丰富的故障特征信息。

表2 样本熵比较

2.2 故障出现对样本熵的影响

时间-小波能量谱反映了轴承信号经小波变换后能量沿时间轴的分布情况，当轴承正常运行时，信号序列中并没有明显能量峰值的出现，此时信号序列复杂程度相对保持稳定；当故障出现时，在故障发生的时刻信号能量会出现峰值，导致信号序列复杂程度发生变化，反映到时间-小波能量谱样本熵上就是样本熵值大小会有明显变化。据此推断，时间-小波能量谱样本熵对轴承运行中出现的早期故障较为敏感。

为证实上述推断，本文分析了轴承从正常运行至发生不同类型故障时时间-小波能量谱样本熵的变化情况。选用美国Case Western Reserve University网上公开的滚动轴承故障数据[10]，实验轴承为支撑驱动端电机轴的JEMSKF6025-2RS深沟球轴承，取轴承正常运行与发生不同类型故障时(故障程度最小，直径为0.007 inch)的数据进行计算分析。样本数据长度为8 192个点，各故障类型样本分别在4种不同工况下取得，分别为：工况1(电机转速为1 797 r/min，载荷为0 Hp)、工况2(转速为1 772 r/min，载荷为1 Hp)、工况3(转速为1 750 r/min，载荷为2 Hp)和工况4(转速为1 730 r/min，载荷为3 Hp)。计算每个样本的时间-小波能量谱样本熵，得到滚动轴承从正常运行至分别发生滚动体、内圈和外圈故障时时间-小波能量谱样本熵值的变化情况如表3所示。从表中可知，在4种运行工况下，轴承正常运行时样本的时间-小波能量谱样本熵与出现不同故障类型时样本的样本熵相比，熵值大小均出现不同幅度的减小，并且下降程度较为明显。通过以上分析，证实了前面所做的推断：时间-小波能量谱样本熵对轴承运行过程中出现的早期故障较为敏感，轴承故障一旦发生，熵值大小会出现明显变化。

表3 轴承不同工况运行下时间-小波能量谱样本熵的变化

Fig.3 Time-wavelet energy spectrum SampEns change when bearings work under different conditions

时间-小波能量谱样本熵工况1工况2工况3工况4正常运行0.60990.65270.67490.7120滚动体故障0.50320.52900.57530.6007内圈故障0.27090.22930.25570.3103外圈故障0.11840.05430.06960.0583

3 实验分析

3.1 实验流程

不同故障模式下滚动轴承信号的时间-小波能量谱样本熵大小区分明显，而且轴承正常运行至发生故障时，样本熵值大小也会出现明显变化。因此，时间-小波能量谱样本熵可作为特征参数较为准确地表征轴承信号蕴含的特征信息。基于此，本文提出使用时间-小波能量谱样本熵对轴承进行故障模式智能识别和运行状态检测，具体流程如图4所示。

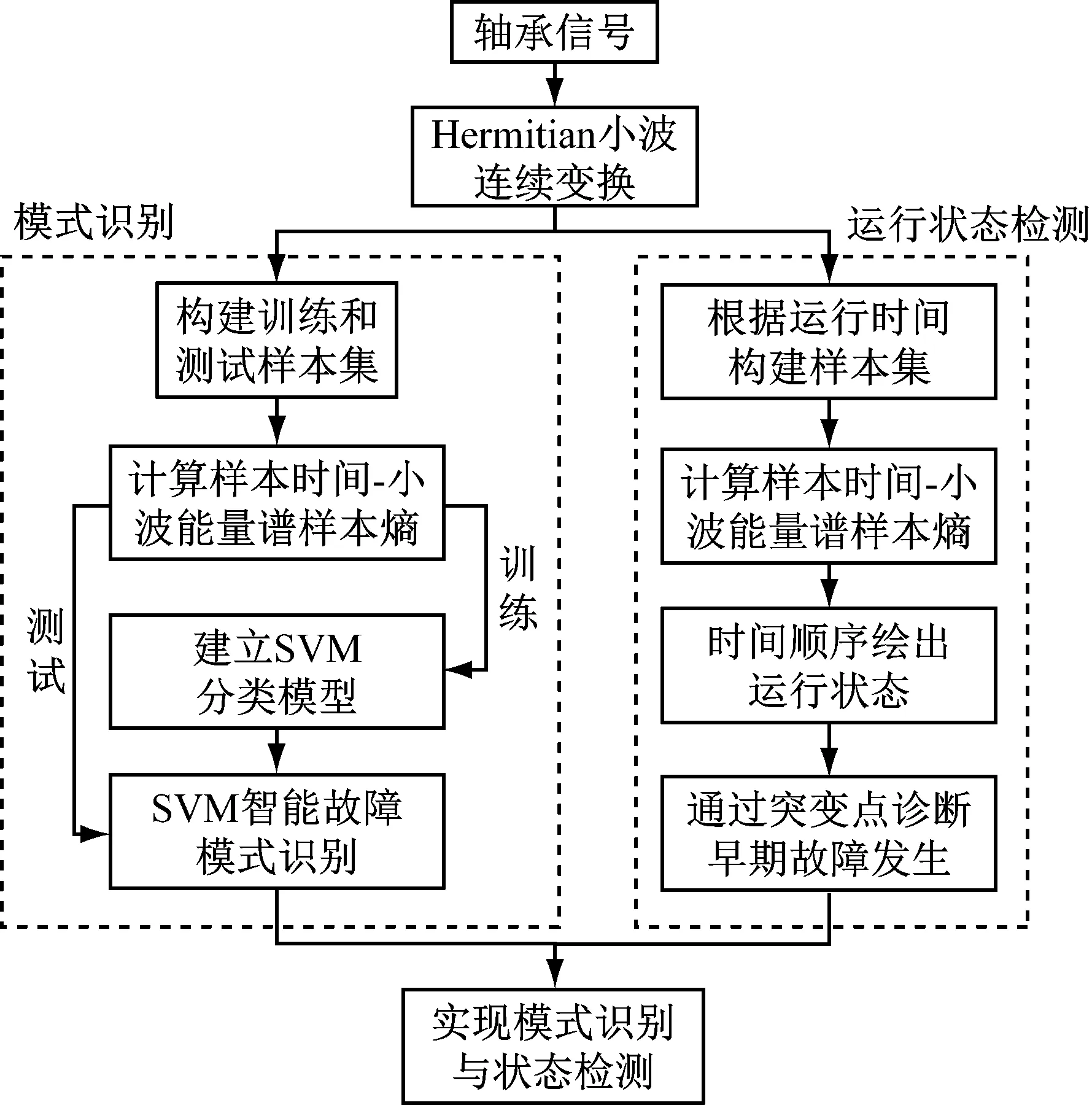
图4 基于时间-小波能量谱样本熵的轴承故障模式识别与运行状态检测流程图

Fig.4 Diagram of fault mode recognition and running state detection of bearing based on time-wavelet energy spectrum sample entropy

3.2 故障模式识别

实验是在QPZZ-II滚动轴承实验台上完成的，图5为实验平台。实验轴承是6205深沟球轴承，利用线切割方式在轴承内、外圈和滚动体上加工宽为0.2 mm、深为1.5 mm的沟槽来模拟轴承实际故障。实验中，转轴转速为1 480 r/min，采样频率为12 800 Hz，每组数据样本长度为5 120点。

图5 轴承试验台结构

首先在轴承正常、滚动体、内圈和外圈故障4种运行模式下，各选取10组样本进行分析，分别计算每组样本的时间-小波能量谱样本熵，结果如图6所示。从图中可知，轴承不同运行模式下，各个样本的时间-小波能量谱样本熵变化较为平稳，波动不大。其中，轴承正常运行时的样本熵与发生各类型故障时区分最为明显；外圈故障区分也较为明显；内圈故障和滚动体故障样本的样本熵值较小，相对较为接近，但彼此相距明显，分离清晰。滚动轴承运行模式不同，相应信号的时间-小波能量谱样本熵值大小也不同，以此作为特征向量可以用于轴承不同故障模式的智能识别。

SVM是一种针对有限数据样本的新型机器学习方法，它不需要采用大量的样本数据对自身模型进行训练，在有限样本和多维模式识别领域具有独特的优势。因此，本文选用SVM方法用于轴承故障模式智能识别，选择径向基核函数建立“一对多”类型的SVM分类模型，设置参数为δ=0.2，C=0.1。在轴承4种运行模式中各采集40组数据样本用于分析，共160组。其中，每个模式下随机选取10组为训练样本，30组为测试样本。计算每组样本的时间-小波能量谱样本熵作为特征向量，先通过训练样本建立SVM，并进行SVM模型的有效性测试，然后再将测试样本特征向量输入到SVM，进行轴承故障模式智能识别。

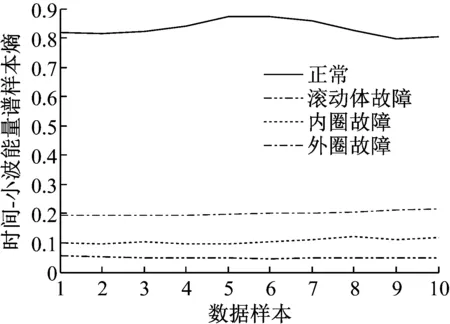
图6 不同运行模式下时间-小波能量谱样本熵分布

Fig.6 The distribution of time-wavelet energy spectrum SampEns under different working states

为进行对比，本文采用基于小波包变换的样本熵方法对相同数据样本也进行轴承故障模式识别，选取“db12”小波，对样本信号经过3层小波包分解后，计算每个子频带信号的样本熵，并将其作为特征向量输入到SVM进行识别，该方法具体步骤可参考文献[4]。上述两种方法智能识别的结果如表4所示，从中可知，两种方法对于测试样本的分类准确率均为100%，因此建立的SVM分类效果较好。本文方法中，轴承滚动体故障和内圈故障测试样本中各有一个样本被错分，120组测试样本的识别准确率为98.3%；小波包样本熵方法中，滚动体故障样本中有一个被错分，识别准确率为99.1%，两种方法识别准确率非常接近，均能实现对滚动轴承不同故障模式的准确识别，这也证实了本文方法的有效性。需要指出的是，本文方法识别轴承故障模式所用的时间要远小于小波包样本熵方法，这是因为小波包样本熵方法需要计算信号小波包分解后每个子频带信号的样本熵，每个样本中包含8个特征向量，而本文方法只需在各个样本中提取1个特征向量。因此，本文所提方法计算量更小，识别效率更高。

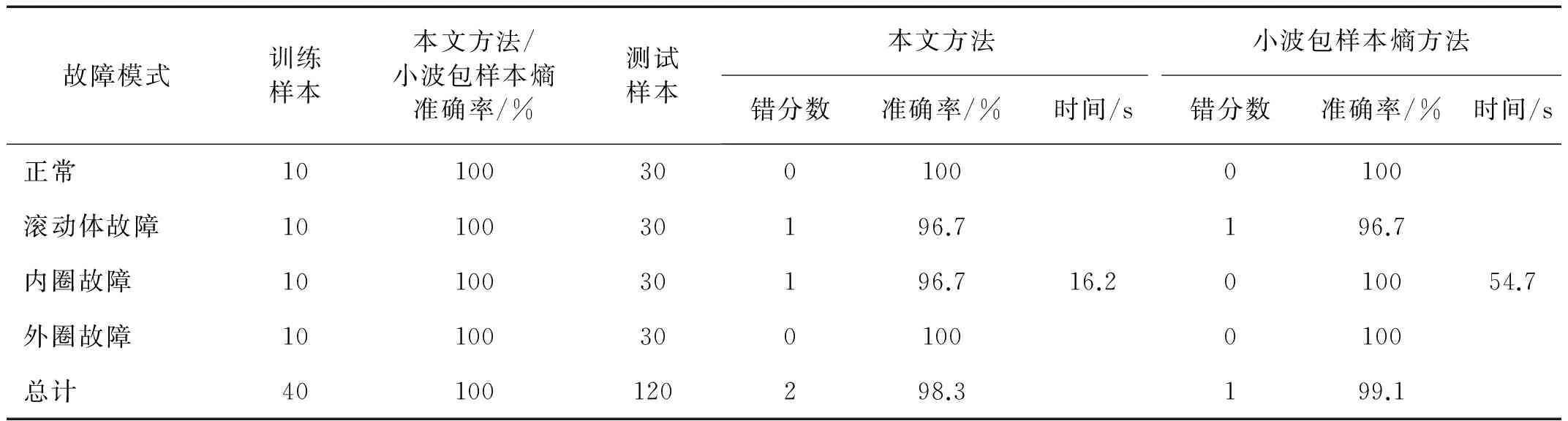
表4 轴承故障模式识别结果

3.3 运行状态检测

美国辛辛那提大学智能维护系统(Intelligent Maintenance Systems,IMS)的全寿命周期轴承实验[11]记录了轴承从正常工作状态到故障发生至一定程度时的变化过程，本文以此数据用于滚动轴承运行状态检测分析。轴承全寿命周期实验平台示意图如图7所示，在转轴上安放有4个测试的滚动轴承，振动信号通过6062E数据采集卡每隔10 min采集一次，采样频率为20 000 Hz。每组数据长度为20 480点，实验结束之后，编号为1的轴承出现了非常严重的外圈故障。

图7 轴承全寿命周期实验平台

选取实验测试数据中的前732组数据进行分析，计算每组数据的时间-小波能量谱样本熵，然后按照轴承运行的时间顺序绘制出时间-小波能量谱样本熵值的变化曲线，结果如图8所示。从图中可知，在轴承开始运行后，振动信号的时间-小波能量谱样本熵值虽然有小幅度波动，但整体波动趋势平稳，趋势基本保持不变，这对应轴承正常运行状态下信号时间-小波能量谱样本熵的变化情况；当轴承运行至5 420 min时，熵值开始减小，并且接下来下降趋势非常明显，这说明轴承正常的运行状态已经发生了变化，早期故障已经出现；当运行至6 470 min时，熵值出现了较为明显的下降，但随后一段时间熵值变化较为平稳，说明此时轴承故障程度并不严重；当运行至7 020 min时，时间-小波能量谱样本熵出现剧烈下降，说明此时轴承故障已经较为严重。观察时间-小波能量谱样本熵检测到的轴承运行状态变化趋势，可知在5 420 min时，轴承出现了较为轻微的早期故障。

图8 时间-小波能量谱样本熵检测

本文所选用的实验平台及实验数据与文献[12]中所选用的完全相同，根据后者的研究结果证实当轴承运行至5 410 min时出现了较为微弱的早期故障，这与图8中的检测结果非常接近，从而验证了时间-小波能量谱样本熵用于检测轴承运行状态的有效性和准确性。

轴承信号的峭度指标与轴承转速、尺寸及所受载荷无关，一旦轴承发生早期故障，峭度值就会增大，因此该指标常用于描述轴承的运行状态。峭度值的计算表达式为[13]

(11)

式中，μ和σ分别为信号的均值和标准差。计算每组数据的峭度值，按照时间顺序排列，得到描述轴承运行状态变化的峭度图如图9所示。从图中可知，轴承开始运行后，峭度指标基本保持平稳，峭度值变化范围不大；运行至6 470 min时，峭度值突然增大，但随后一段时间峭度值变化较为平稳，说明峭度指标检测出轴承的运行状态出现了异常，但故障程度并不严重；运行至7 020 min时，峭度值开始剧烈增大，变化非常明显，说明此时轴承已出现了较为严重的故障。峭度指标检测轴承运行状态各个阶段的变化与时间-小波能量谱检测结果相一致，但峭度检测发现轴承早期故障的时间要比时间-小波能量谱样本熵晚1 050 min。

图9 峭度指标检测

4 结 论

本文基于Hermitian连续小波变换和样本熵理论，提出了时间-小波能量谱样本熵的计算方法，将其作为特征参数用于滚动轴承故障智能诊断研究，通过实验分析，验证了所提方法的有效性，得到相关结论如下：

(1) Hermitian小波具有较好的信号奇异性检测和瞬时相位识别能力。连续小波变换后得到的时间-小波能量谱反映了信号能量在时间域内的分布状况，其中蕴含了轴承的故障特征信息。

(2) 轴承在不同故障模式下，得到的时间-小波能量谱序列的自相似性和复杂程度有较大区别，样本熵值区分明显。将其作为特征向量输入SVM，能较为准确地实现轴承故障模式的智能识别。

(3) 轴承运行出现故障时，信号的时间-小波能量谱样本熵将发生明显变化，通过绘制时间-小波能量谱样本熵的变化曲线，可以对轴承的运行状态进行检测，相比峭度方法可以更早地诊断出轴承早期故障的发生。

[1] MENG Lingjie, XIANG Jiawei, ZHONG Yongteng, et al. Fault diagnosis of rolling bearing based on second generation wavelet denoising and morphological filter[J]. Journal of Mechanical Science and Technology, 2015, 29(31):3121-3129.

[2] 王小玲，陈进，从飞云. 基于时频的频带熵方法在滚动轴承故障识别中的应用[J]. 振动与冲击，2012,31(18):29-33.

WANG Xiaoling, CHEN Jin, CONG Feiyun. Application of spectral band entropy (SBE) method in rolling bearing fault diagnosis based on time-frequency analysis[J]. Journal of Vibration and Shock, 2012,31(18):29-33.

[3] 赵志宏, 杨绍普. 一种基于样本熵的轴承故障诊断方法[J]. 振动与冲击, 2012,31(6):136-140.

ZHAO Zhihong, YANG Shaopu. Sample entropy-based roller bearing fault diagnosis method[J]. Journal of Vibration and Shock, 2012,31(6):136-140.

[4] 赵志宏, 杨绍普. 基于小波包变换与样本熵的滚动轴承故障诊断[J]. 振动、测试与诊断, 2012,32(4):640-644.

ZHAO Zhihong, YANG Shaopu. Roller bearing fault diagnosis based on wavelet packet transform and sample entropy[J]. Journal of Vibration, Measurement and Diagnosis, 2012, 32(4):640-644.

[5] 冯辅周, 司爱威, 饶国强,等. 基于小波相关排列熵的轴承早期故障诊断技术[J]. 机械工程学报, 2012, 48(13):73-79.

FENG Fuzhou, SI Aiwei, RAO Guoqiang, et al. Early fault diagnosis technology for bearing based on wavelet correlation permutation entropy[J]. Journal of Mechanical Engineerin, 2012, 48(13):73-79.

[6] SSU C H H, SA L D, LI W G. Hermitian hat wavelet design for singularity detection in the Paraguay river level data analyses[C]//Proceeding of the International Society for Optical Engineering. California: Proceedings of SPIE, 1997.

[7] LI Hui, ZHANG Yuping, ZHENG Haiqi. Application of Hermitian wavelet to crack fault detection in gearbox[J]. Mechanical Systems and Signal Processing, 2011, 25(4):1353-1363.

[8] LI Hui, FU Lihui, ZHENG Haiqi. Bearing fault diagnosis based on amplitude and phase map of Hermitian wavelet transform[J]. Journal of Mechanical Science and Technology, 2011, 25(11):2731-2740.

[9] 张进，冯志鹏，褚福磊. 滚动轴承故障特征的时间-小波能量谱提取方法[J]. 机械工程学报，2011,47(17)：44-49.

ZHANG Jin, FENG Zhipeng, CHU Fulei. Extraction of rolling bearing fault feature based on time-wavelet energy spectrum[J]. Chinese Journal of Mechanical Engineerin, 2011,47(17):44-49.

[10] The case western reserve university bearing data center[EB/OL]. http://csegroups.case.edu/bearingdatacenter/ pages/ download-data-file.

[11] WANG Yi, XU Guanghua, LIANG Lin, et al. Detection of weak of transient signals based on wavelet packet transform and manifold learning for rolling element bearing fault diagnosis[J]. Mechanical Systems and Signal Processing, 2015, 54/55:259-276.

[12] 唐贵基, 王晓龙. 自适应最大相关峭度解卷积在滚动轴承早期故障诊断中的应用[J].中国电机工程学报, 2015, 35(6):1436-1444.

TANG Guiji, WANG Xiaolong. Adaptive maximum correlated kurtosis deconvolution method and its application on incipient fault diagnosis[J]. Proceedings of CSEE, 2015,35(6):1436-1444.

[13] 胡爱军，马万里，唐贵基. 基于集成经验模态分解和峭度准则的滚动轴承特征提取方法[J]. 中国电机工程学报，2012，32(11)：106-111.

HU Aijun, MA Wanli, TANG Guiji. Rolling bearing fault feature extraction method based on ensemble empirical mode decomposition and kurtosis criterion[J]. Proceedings of the CSEE, 2012, 32(11):106-111.

An intelligent method for rolling element bearing fault diagnosis based on time-wavelet energy spectrum sample entropy

DENG Feiyue1, TANG Guiji2

(1. Department of Mechanical Engineering, Shijiazhuang Tiedao University, Shijiazhuang 050043, China;2. School of Energy, Power and Mechanical Engineering, North China Electric Power University, Baoding 071003, China)

In order to solve the problem of fault mode intelligent recognition and running state detection of rolling element bearing, a new method called time-wavelet energy spectrum sample entropy as the characteristic parameter was proposed for bearing fault intelligent diagnosis. Time-wavelet energy spectrum which contained fault information of bearing was obtained through the Hermitian wavelet continuous wavelet transform, and fault feature was quantitatively extracted by calculating the sample entropy of the energy spectrum. The time-wavelet energy spectrum sample entropies of bearings under different fault modes could be distinguished clearly, which could be treated as input characteristic vectors of a support vector machine (SVM) in order to complete the intelligent recognition of different fault modes of bearings. Next, the trend of running state of bearing was acquired through calculating the time-wavelet energy spectrum sample entropy of data from the whole life cycle test rig of bearing and arranging them chronologically. The early damage occurring in bearing could be effectively detected by judging the running state trend. Practical examples show the proposed method can be applied to the research for intelligent diagnosis of rolling element bearing efficiently.

rolling element bearing; intelligent diagnosis; continuous wavelet transform; sample entropy; support vector machine (SVM)

河北省自然科学基金(E2014502052)；中央高校基本科研业务专项资金项目(2014XS83)

2016-01-05 修改稿收到日期：2016-03-17

邓飞跃 男，博士,讲师,1985年11月生 E-mail:dengfeiy@126.com

TP206

A

10.13465/j.cnki.jvs.2017.09.005