考虑轮胎侧偏特性的赛车转向几何研究

柴 天 李 凡 雷 飞 刘 杰 曾 侠 唐应时

1.湖南大学汽车车身先进设计制造国家重点实验室，长沙，4100822.湖南大学机械与运载工程学院，长沙，410082

考虑轮胎侧偏特性的赛车转向几何研究

柴 天1,2李 凡1,2雷 飞1,2刘 杰1,2曾 侠2唐应时1,2

1.湖南大学汽车车身先进设计制造国家重点实验室，长沙，4100822.湖南大学机械与运载工程学院，长沙，410082

为了提高赛车轮胎侧向附着合力及转向极限侧向加速度，提出了一种考虑轮胎侧偏特性的转向几何。通过分析轮胎侧偏角的影响，确定了整车转向瞬心位置，并建立了三自由度整车模型。结合轮胎力学模型，以最大化整车轮胎侧向附着合力为目标，采用隔代映射遗传算法对考虑轮胎侧偏特性的转向几何进行求解。整车仿真和试验结果表明，相比阿克曼转向几何，考虑轮胎侧偏特性的转向几何可以更有效地增大整车轮胎的侧向附着合力，提高赛车在极限工况下的转弯性能。

转向几何；轮胎侧偏特性；轮胎侧向力；优化；赛车

0 引言

赛车运动期望车辆在赛道上以尽可能短的时间完成既定里程，因此，车辆需以尽可能高的平均速度完成比赛。然而赛道往往由各种直道和弯道组成，赛车在直道中会加速、在弯道中需减速以顺利通过弯道，所以，为了提高赛车的平均速度，需要提高赛车加速时的纵向加速度、制动时的纵向减速度以及转向时的侧向加速度[1]。提高侧向加速度可使赛车以更快的车速转向，从而提高赛车在弯道中的平均速度；而且由于转向车速提高，赛车在进入弯道前可以不过多地减速，出弯时能以更高的初速进行加速，也有利于提高赛车直道的平均速度，因此，转向性能对赛车至关重要。

目前，国内外学者对车辆转向性能开展了众多研究。初亮等[2]考虑独立悬架断开点对转向梯形运动的影响，建立了断开式转向梯形机构的数学模型并对机构进行了优化设计。董恩国等[3]研究了设计变量的随机误差对转向机构的影响，减少了不确定因素对车辆转向性能的影响。文献[4-5]研究了转向和悬架之间的相互作用。SIMIONESCU等[6]对二自由度转向机构进行了运动学分析，并对其性能进行了研究。MIHAILIDIS等[7]设计了一种可调节的转向梯形机构，使车辆可以满足不同工况的性能需求。

上述研究基本是在阿克曼转向几何基础上对转向系统进行研究的，这对车辆转向系统的工程开发有很好的指导意义。但阿克曼几何未考虑轮胎的侧偏特性，且赛车更关注轮胎附着力的提高，以使整车获得更大的加速度。本文考虑轮胎侧偏特性的影响，提出了一种满足赛车性能需求的转向几何。首先，建立考虑轮胎侧偏特性的三自由度整车转向模型；然后，结合轮胎力学模型，以最大化整车轮胎侧向附着合力为目标，采用隔代映射遗传算法对考虑轮胎侧偏特性的转向几何进行求解；最后，通过整车动力学仿真和整车试验对这种转向几何的性能进行验证。

1 整车转向动力学建模

转向几何的确定，关键在于确定整车转向瞬心位置。阿克曼转向几何没有考虑轮胎侧偏特性，将转向瞬心定位于后轴延长线上。但赛车通常会以很大的侧向加速度进行转向，使赛车轮胎产生很大的侧偏角，转向瞬心也大幅度前移，所以阿克曼转向几何很难适用于赛车。

若整车转向为定半径稳态回转运动，则转向瞬心将位于以质心为圆心、转弯半径为半径的圆周上。由于轮胎侧偏角的影响，转向瞬心将沿该圆周前移，故由此可确定前移后转向瞬心的位置和对应的各轮胎侧偏角。同时，由于侧偏角与侧向附着力相关，进而可对转向几何与整车轮胎侧向附着合力的关系进行研究。

1.1 整车模型

忽略空气动力学和悬架跳动的影响，并假设轮胎的倾角和束角均为0、整车转向为定半径稳态回转运动，则可建立包含纵向、侧向和横摆运动的三自由度整车转向模型(图1)。图中，R为整车稳态回转运动的半径；I为整车转向瞬心；O为整车质心；u、v、ω分别为整车质心位置上的纵向速度、侧向速度和横摆角速度，且侧向速度v的方向指向瞬心；纵向速度u与整车纵轴的夹角δ为质心侧偏角，图中所示方向为负值，δ越大,表明瞬心的前移量越大；l、tf、tr分别为整车的轴距和前后轮距；a、b分别为质心与前后轴的距离。

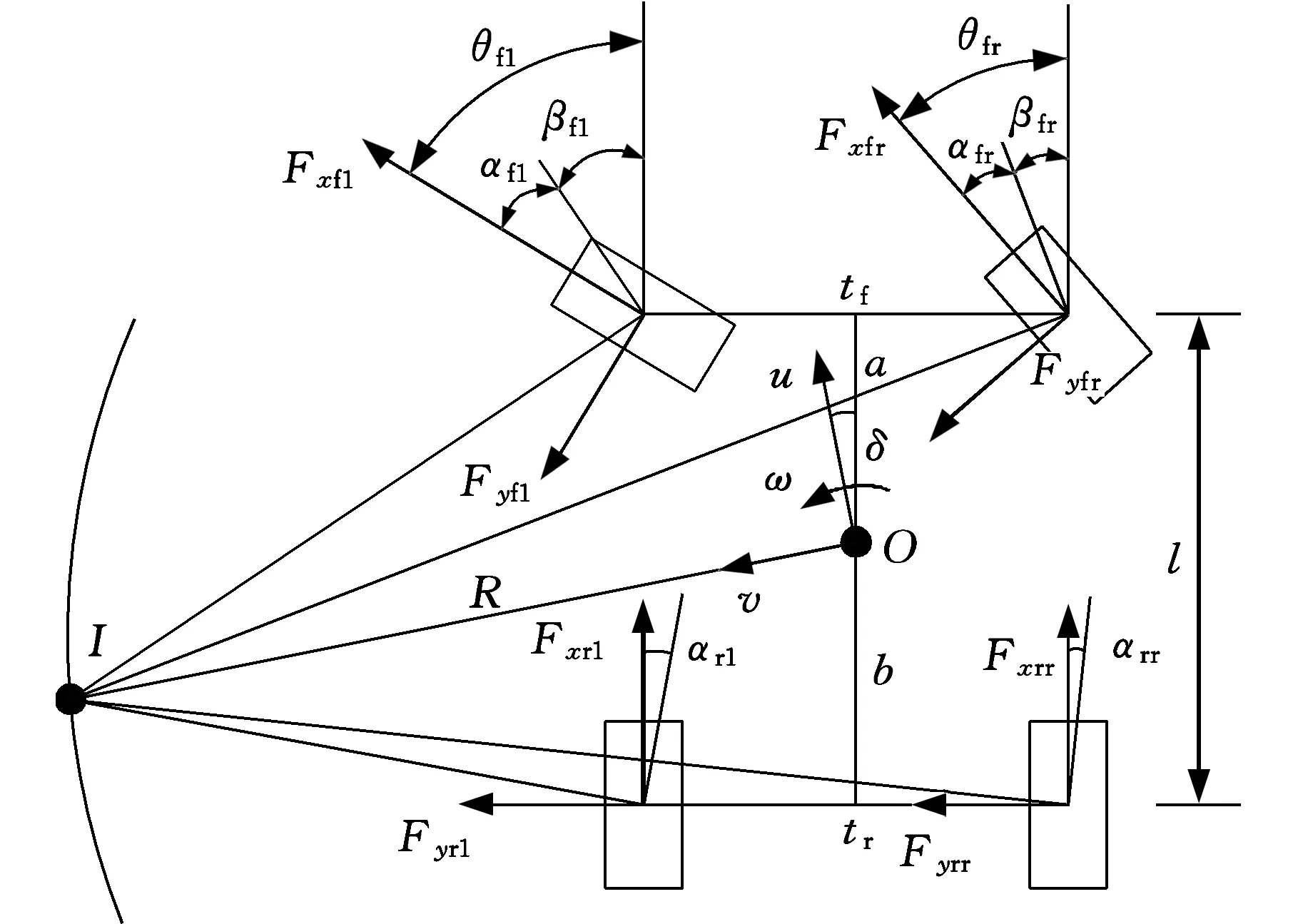
图1 三自由度整车转向模型Fig.1 3-DOF car steering model

根据牛顿第二定律，三自由度整车转向模型的动力学方程为

Fyfrsin(θfr+δ)+Fxflcos(θfl+δ)-Fyflsin(θfl+δ)+

(Fxrr+Fxrl)cosδ-(Fyrr+Fyrl)sinδ

(1)

Fyfrcos(θfr+δ)+Fxflsin(θfl+δ)+Fyflcos(θfl+δ)+

(Fxrr+Fxrl)sinδ+(Fyrr+Fyrl)cosδ

(2)

Fxrrtr/2-Fyrrb-Fxrltr/2-Fyrlb=0

(3)

θj=αj+βj

(4)

(5)

(6)

式中，Fu、Fv分别为各轮胎附着力在纵向速度u和侧向速度v方向上的分力；Mz为各轮胎附着力对质心O的横摆力矩；m为整车质量；Iz为整车绕过质心竖直轴的转动惯量；Fxi为轮胎的纵向附着力，i=fr,fl,rr,rl；Fyi为轮胎的侧向附着力；θj为前轮转角，j=fr,fl；αi为轮胎侧偏角；βi为轮胎速度方向与整车纵轴的夹角；d1、d2、d3、d4分别为轮胎附着力对整车质心的力臂。

1.2 轮胎模型

由上述模型可知，当转弯半径R和质心侧偏角δ确定时，即可确定转向瞬心位置和各轮胎的侧偏角，进而可由PAC2002魔术公式轮胎模型[8]计算轮胎的侧向附着力Fy，即

Fy=Dsin{Carc tan[Bα-EBα+Earctan(Bα)]}+Svy

(7)

式中，D、C、B、E分别为峰值因子、形状因子、刚度因子和曲率因子；Svy为曲线偏移量；α为轮胎侧偏角。

赛车轮胎采用特殊配方设计，其附着系数明显高于普通轮胎附着系数[1]。通过对典型的大学生方程式赛车轮胎进行试验[9]，获得轮胎力学特性试验数据，并根据试验数据对PAC2002魔术公式轮胎模型的各项因子进行拟合，所获得轮胎模型的力学特性如图2所示。

图2 轮胎的力学特性Fig.2 Mechanical properties of racing tire

通过上述轮胎模型计算轮胎的侧向附着力，需获取各轮胎的垂向载荷。载荷转移后各轮胎的垂向载荷[10]

Fzi=Fz0i+ΔFsi+ΔFui

(8)

其中，Fz0i为静平衡状态下各轮胎的垂向载荷；ΔFsi、ΔFui分别为簧载质量和非簧载质量转移引起的轮胎垂向载荷变化量，即

式中，ay为整车侧向加速度；ms、mu分别为整车簧载质量和非簧载质量；msf、msr分别为前后轴簧载质量；muf、mur分别为前后轴非簧载质量；kf、kr分别为前后悬架侧倾刚度；hz为簧载质量质心与侧倾轴线的距离；hrf、hrr分别为前后悬架侧倾中心高度；huf、hur分别为前后轴非簧载质量的质心高度。

对于轮胎的纵向附着力，由于前轮为从动轮，故可认为其纵向附着力为轮胎的滚动阻力，其计算公式为

(9)

式中，μ为轮胎滚动阻力系数。

后轮为驱动轮，其纵向附着力为驱动力。假设差速器的锁紧系数为0，则两后轮的纵向附着力相同。当已知各轮胎侧向附着力、前轮纵向附着力以及整车运动状态时，通过式(1)即可求出后轮的纵向附着力。

2 考虑侧偏特性的转向几何求解

由式(4)可知，前轮转角直接影响轮胎侧偏角的大小，从而影响轮胎的侧向附着力，所以，为增大整车轮胎的极限侧向附着合力，以提高赛车转向时的极限侧向加速度，可以将对考虑轮胎侧偏特性转向几何的求解等效为对最大化整车侧向附着合力的优化问题。

2.1 优化问题

整车轮胎侧向附着合力越大，侧向加速度越大，因此，以侧向附着合力为优化目标函数。由轮胎侧偏特性可知，轮胎侧偏角与轮胎侧向附着力直接相关。又由式(4)和式(5)可知，当转弯半径R确定时，可由两前轮转角θfr、θfl和质心侧偏角δ确定各轮胎的侧偏角，故将其作为优化设计向量X =(θfr,θfl,δ)。

质心侧偏角δ过大将会降低车辆横向稳定性，为此，取δ的约束为±12°[11]。由于改变整车运动状态的外力均来自轮胎附着力，故附着合力受整车运动状态约束。又由于假设整车转向为定半径稳态回转运动，故在该运动状态下整车纵向速度u和横摆角速度ω均为常数，且侧向速度v=0。根据式(1)～式(3)，轮胎附着合力应满足等式∑Fu=0,∑Fv=muω和∑Mz=0。综上所述，并令ay=uω，则整车侧向附着合力的优化问题可描述为

(10)

采用隔代映射遗传算法(IP-GA)[12]进行求解，该算法是对小种群遗传算法(μGA)的改进。在μGA能够避免收敛早熟、可以快速寻找到最优区域等优点的基础上，IP-GA在μGA中加入了IP算子，通过连续两代之间的最优个体来构造移动方向以快速获得更优的个体，从而增强对全局最优解的搜索能力，并大大提高了收敛速度。由于在某一确定的转弯半径下只能求解出所对应的内外前轮转角，故对式(10)的优化模型分别在不同转弯半径下进行求解，即可得到一定转角范围内的内外前轮转角关系。

2.2 优化结果

以某型大学生方程式赛车为例，求解考虑轮胎侧偏特性转向几何，并确定前轮转角关系，其整车相关参数见表1。根据大学生方程式赛车比赛赛道的特点，赛车转弯半径多在4.5～25 m之间；但为满足前轮转角设计范围的需要，在3.5～45 m范围内对前轮转角关系进行求解，须考虑轮胎侧偏特性转向几何所确定的前轮转角关系，如图3和表2所示。

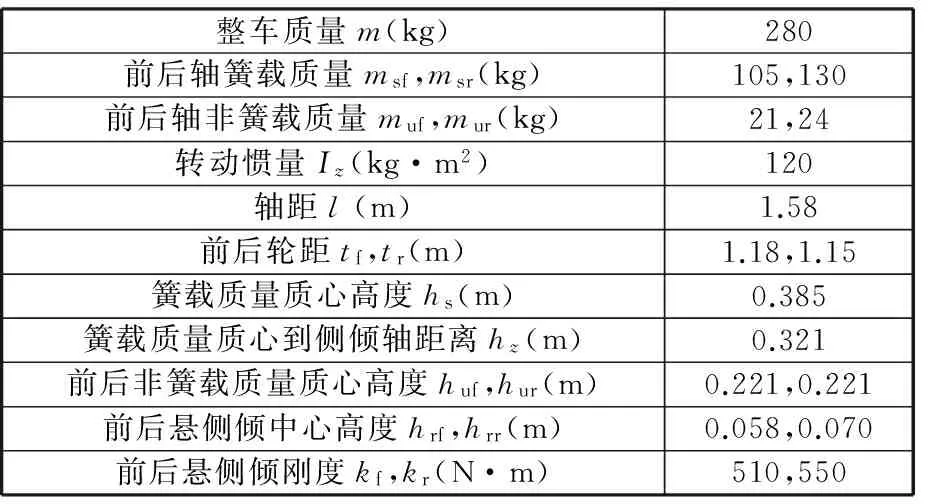
表1 赛车相关参数Tab.1 Parameter of racing car

图3 前轮转角关系Fig.3 Relation of front wheel steering angles表2 两种转向几何下的前轮转角对比Tab.2 Front wheel steering angles of bothsteeing geometries

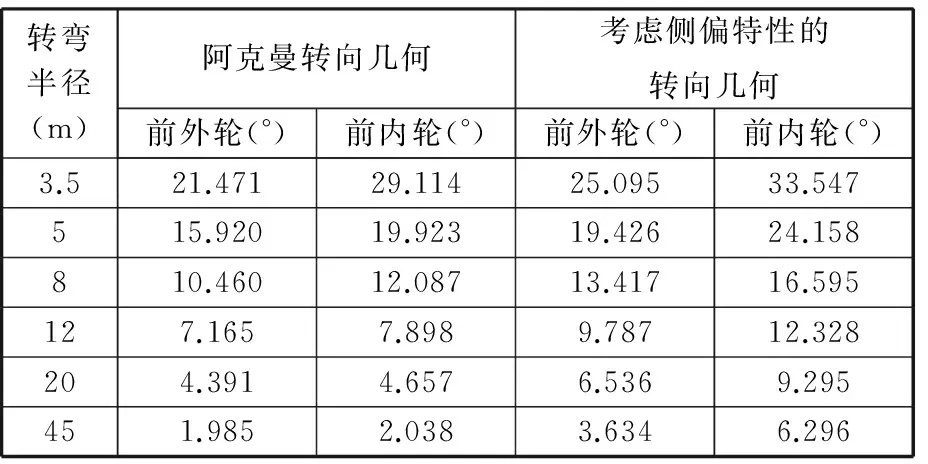
转弯半径(m)阿克曼转向几何考虑侧偏特性的转向几何前外轮(°)前内轮(°)前外轮(°)前内轮(°)3.521.47129.11425.09533.547515.92019.92319.42624.158810.46012.08713.41716.595127.1657.8989.78712.328204.3914.6576.5369.295451.9852.0383.6346.296

2.3 分析与讨论

由图3和表2可知，在3.5～45 m的转弯半径范围内，考虑轮胎侧偏角影响的转向几何与传统阿克曼转向几何确定的前轮转角关系有明显区别，相同转弯半径下两种转向几何内外前轮的转角也有很大差别。

为使整车产生侧向加速度，需要轮胎提供侧向附着力，则轮胎会产生侧偏角。后轮侧偏角会使整车转向瞬心从后轴延长线向前偏移，表现为质心侧偏角增大。相较阿克曼转向几何，瞬心位置的变化使相同转弯半径所对应的前轮速度方向发生变化，从而导致前轮转角变化。又由于前轮也会产生侧偏角，从而进一步改变前轮转角。图4、图5所示分别为考虑轮胎侧偏特性转向几何在最大侧向加速情况下的轮胎侧偏角和质心侧偏角曲线，由图可知，轮胎产生很大的侧偏角，而且质心侧偏角也很大，这表明转向瞬心有很大的前移量。所以，在前后轮胎侧偏特性的共同作用下，考虑轮胎侧偏特性的转向几何与阿克曼转向几何产生了明显的差异。

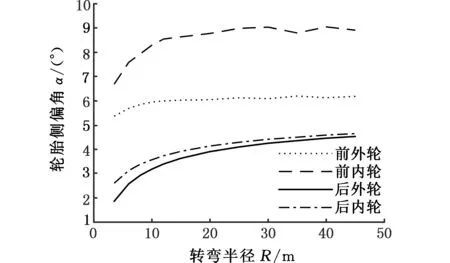
图4 轮胎侧偏角曲线Fig.4 Curve of slip angles of tire

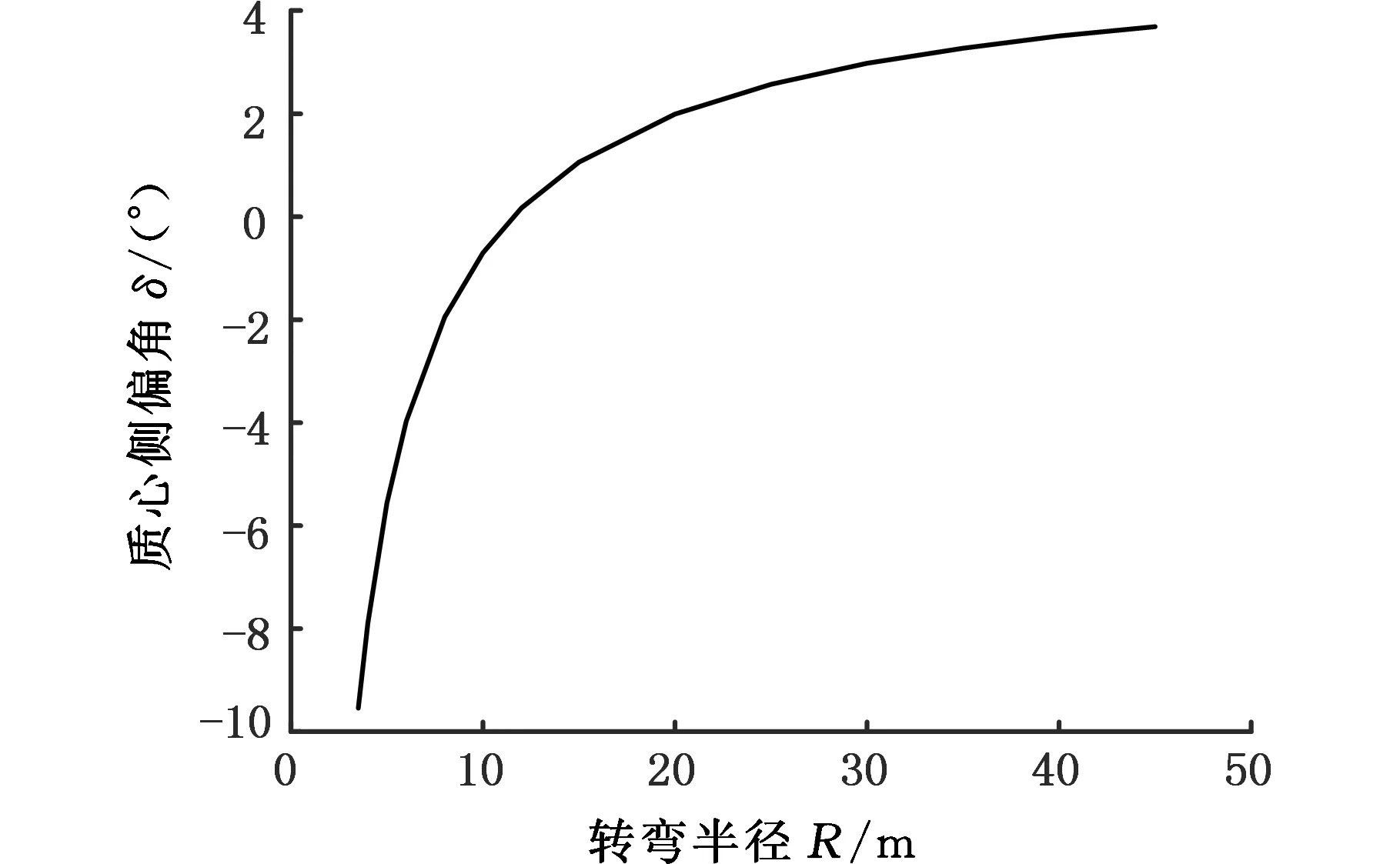
图5 质心侧偏角曲线Fig.5 Curve of vehicle side slip angle

3 整车仿真和试验验证

3.1 整车稳态回转仿真

分别采用阿克曼转向几何和考虑轮胎侧偏特性的转向几何，在ADAMS/Car中建立某型大学生方程式赛车的多体动力学仿真模型[13]，并对整车的稳态回转进行仿真分析。不同转弯半径下，赛车稳态回转的最大侧向加速度仿真结果如图6所示。

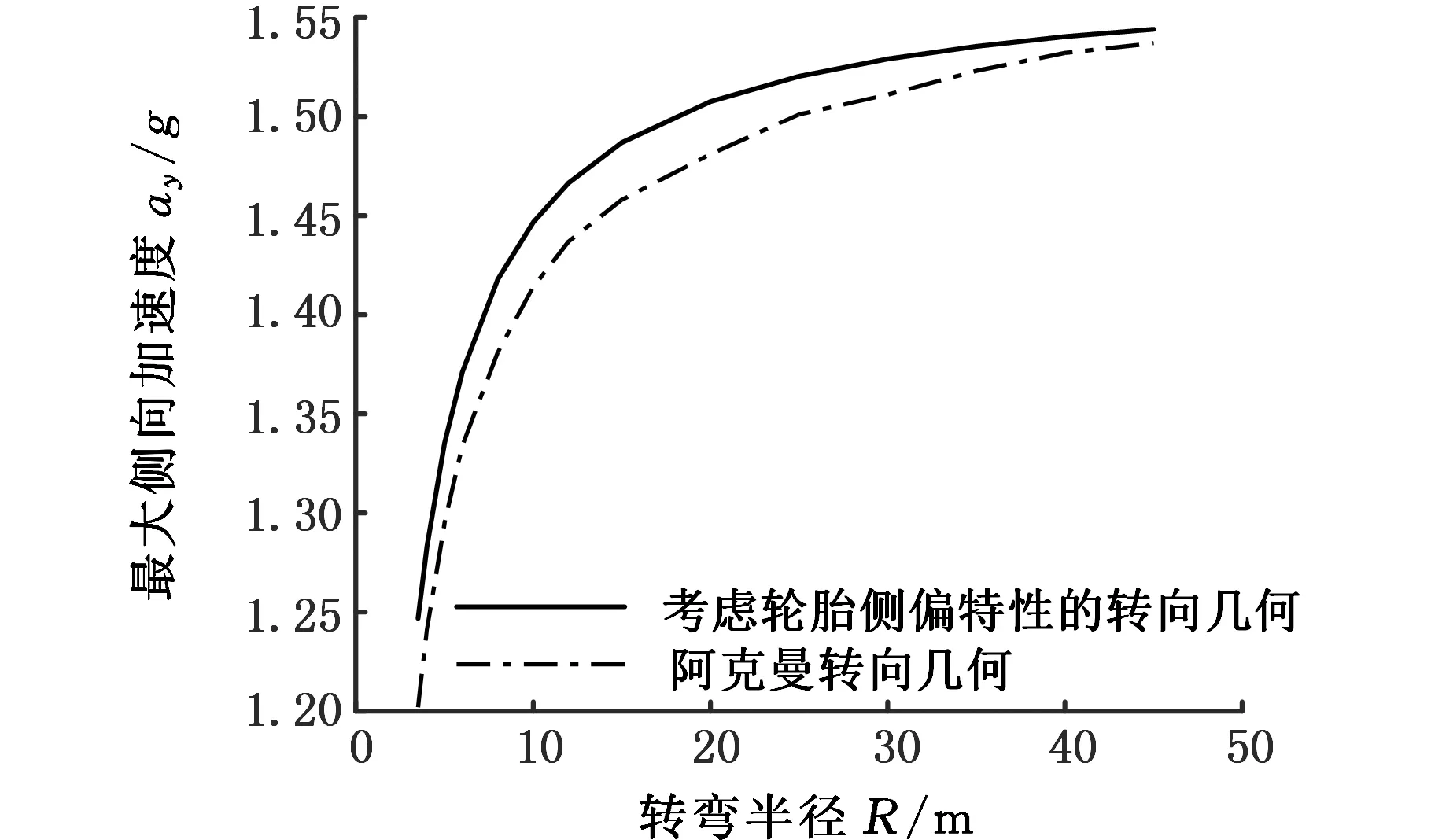
图6 不同转弯半径下两种转向几何的最大侧向加速度Fig.6 Maximum lateral acceleration vs. turning radius

由图6可知，考虑轮胎侧偏特性的转向几何可以提高整车的最大侧向加速度，故该转向几何可以增大整车轮胎的侧向附着合力。随着转弯半径的增大，最大侧向加速度的增量逐渐减小，其原因是当转弯半径较小时，最大侧向加速度较小，则整车侧向载荷转移量较小，内侧轮胎仍有较大垂向载荷来产生侧向附着力，所以通过改善内外前轮转角关系可以有效增大整车轮胎的侧向附着合力，进而提高整车的侧向加速度。而当转弯半径增大时，最大侧向加速度增大，整车侧向载荷转移使内侧轮胎的垂向载荷明显减小，无法产生对整车运动有明显影响的侧向附着力，所以通过改善内外前轮转角关系，也无法对整车的侧向加速度产生显著的影响。

3.2 整车试验验证

为验证考虑轮胎侧偏特性转向几何的实际效果，使用某型大学生方程式赛车对整车稳态回转性能进行试验。通过对赛车转向机构进行改装，获得不同的转向几何，实现对不同转向几何的转向性能对比。试验用大学生方程式赛车如图7所示。

图7 试验用大学生方程式赛车Fig.7 Formula student racing car for experiment

赛车以尽可能大的侧向加速度进行稳态回转时，其车速和侧向加速度有较大浮动。为便于对试验结果进行分析，可通过赛车完成整圈稳态回转的最短时间来计算赛车的侧向加速度。虽然计算结果为最大平均侧向加速度，但不影响对两种转向几何的优劣进行对比和对侧向加速度的变化趋势进行分析。试验结果见表3。

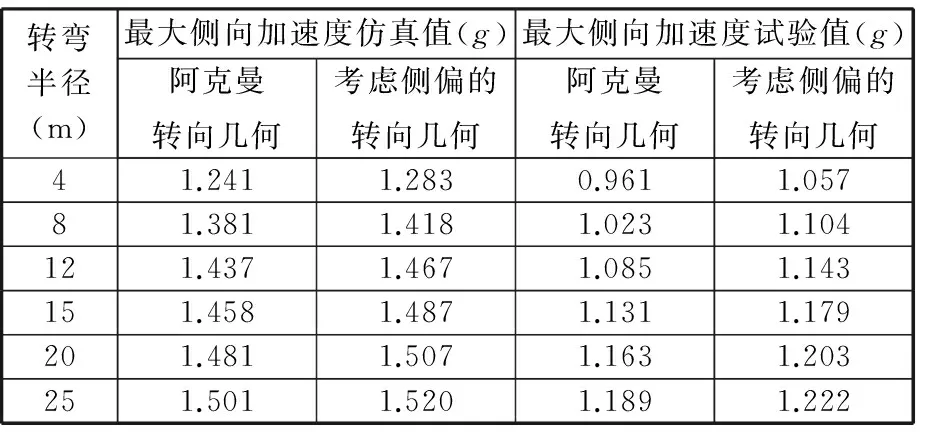
表3 整车试验结果Tab.3 Vehicle experiment results

由表3可知，整车稳态回转试验的侧向加速度数据低于ADAMS/Car仿真数据。这是由多种因素综合作用所造成的，包括轮胎与试验场地路面的实际附着情况、ADAMS/Car多体动力学模型和实车的误差、试验员驾驶水平以及试验结果为平均侧向加速度等。由试验结果可知，在不同转弯半径下，考虑轮胎侧偏特性转向几何的最大侧向加速度均大于阿克曼转向几何的最大侧向加速度，且两种几何的加速度差值随转弯半径的增大而减小。上述变化趋势与ADAMS/Car仿真结果基本一致。这说明采用考虑轮胎侧偏特性的转向几何可以有效增大整车轮胎的极限侧向附着合力，提高整车的极限侧向加速度。

4 结论

(1)本文提出的转向几何在确定整车转向瞬心时考虑了轮胎侧偏特性，使其不仅考虑了轮胎侧偏角对轮胎滚动方向的影响，而且考虑了轮胎力学特性对整车侧向加速度的影响。

(2)相比阿克曼转向几何，考虑轮胎侧偏特性的转向几何可以有效增大整车轮胎的极限侧向附着合力，提高整车的极限侧向加速度，提高整车在极限工况下的转向性能。

(3)由于后轮侧偏角将使整车转向瞬心前移，从而影响前轮转角，故赛车转向几何的优化设计应当综合考虑前后轮胎的影响。

[1] MILLIKEN W F, MILLIKEN D L. Race Car Vehicle Dynamics[M].Warrendale: Society of Automotive Engineers, Inc.,1995.

[2] 初亮, 鲁和安, 彭彦宏, 等. 空间机构学理论在断开式转向梯形分析及优化中的应用[J]. 农业机械学报,1999,30(4):77-82. CHU Liang, LU Hean, PENG Yanhong, et al. Theory of Spatial Mechanism Applying on the Analysis and Optimization of the Splitting Ackerman Steering Linkage[J]. Transactions of the Chinese Society for Agriculture Machinery,1999,30(4):77-82.

[3] 董恩国, 张蕾, 关志伟.双前桥转向机构稳健设计的研究[J].汽车工程,2013,35(8):673-676. DONG Enguo, ZHANG Lei, GUAN Zhiwei. A Study on the Robust Design of Double-front-axle Steering Mechanism[J]. Automotive Engineering,2013,35(8):673-676.

[4] 唐应时, 朱彪, 朱位宇, 等. 基于响应面方法的转向梯形优化设计[J].中南大学学报(自然科学版),2012(7):2601-2606. TANG Yingshi, ZHU Biao, ZHU Weiyu, et al. Optimization of Ackerman Steering Linkage Based on RSM[J]. Journal of Central South University(Science and Technology),2012(7):2601-2606．

[5] 刘振声, 赵亮.双前桥转向系与悬架运动协调性分析及优化[J]. 中国机械工程,2013,24(16):2164-2167.LIU Zhensheng, ZHAO Liang. Motion Compatibleness Analysis and Optimization of Double Front Axle Steering Mechanism and Suspension System[J]. China Mechanical Engineering,2013,24(16):2164-2167.

[6] SIMIONESCU P A, TEMPEA I, LOCH N E. Kinematic Analysis of a Two-degree-of-freedom Steering Mechanism Used in Rigid-axle Vehicles[J]. Proceedings of the Institution of Mechanical Engineers Part D,Journal of Automobile Engineering,2001,215(7):803-812.

[7] MIHAILIDIS A, SAMARAS Z, NERANTZIS I,et al. The Design of a Formula Student Race Car:a Case Study[J]. Proceedings of the Institution of Mechanical Engineers Part D,Journal of Automobile Engineering, 2009,223(6):805-818.

[8] PACEJKAH B. Tyre and Vehicle Dynamics[M]. Amsterdam:Elsevier Butterworth-Heinemann,2006.

[9] KASPRZAK E M, GENTZ D. The Formula SAE Tire Test Consortium-tire Testing and Data Handling[J]. SAE Paper,2006:776-4841.

[10] 余志生.汽车理论[M].3版.北京：机械工业出版社, 2005. YU Zhisheng.Theory of Automobile[M].3rd ed. Beijing: China Machine Press,2005.

[11] 夏光,唐希雯,陈无畏,等.基于轮胎合力计算与分配的车辆横向稳定性控制研究[J]. 汽车工程,2015,37(11):1298-1306. XIA Guang, TANG Xiwen, CHEN Wuwei, et al. A Research on the Lateral Stability Control of Vehicle Based on the Resultant Force Calculation and Allocation of Tire[J]. Automotive Engineering,2015,37(11):1298-1306.

[12] LIUG R, HAN X. Computational Inverse Techniques in Non-destructive Evaluation[M]. Boca Raton:CRC Press,2003.

[13] MUELLERR L. Full Vehicle Dynamics Model of a Formula SAE Racecar Using ADAMS/Car[D]. College Station :Texas A & M University,2005.

(编辑 陈 勇)

Study on Steering Geometry of Racing Cars with Consideration of Tire Cornering Characteristics

CHAI Tian1,2LI Fan1,2LEI Fei1,2LIU Jie1,2ZENG Xia2TANG Yingshi1,2

1.State Key Laboratory of Advanced Design and for Vehicle Body，Hunan University，Changsha，410082 2.College of Mechanical and Vehicle Engineering， Hunan University， Changsha， 410082

For improving the tire lateral resultant forces and lateral accelerations of racing cars, a steering geometry was proposed considering the effects of tire cornering characteristics. The instantaneous center of steering was defined by analyzing the impacts of tire slip angles, and a 3-DOF full vehicle model containing tire model was developed for steering simulation. The steering geometry was obtained via optimization of maximizing lateral resultant forces of tires by IP-GA. Simulations and tests were conducted to validate the theoretical basis of the present steering geometry. The results indicate that the maximum lateral resultant force is raised under the design using the present steering geometry compared with Ackerman steering geometry. Thus the steering performance within extreme condition could be improved.

steering geometry；tire cornering characteristic；tire lateral force；optimization；racing car

2016-11-04

国家自然科学基金资助项目(51205117)

U463.42

10.3969/j.issn.1004-132X.2017.09.018

柴 天，男，1983年生。湖南大学汽车车身先进设计制造国家重点实验室博士研究生。主要研究方向为汽车系统动力学。E-mail: chaitian@hnu.edu.cn。李 凡，男，1981年生。湖南大学汽车车身先进设计制造国家重点实验室助理教授。雷 飞，男，1981年生。湖南大学汽车车身先进设计制造国家重点实验室助理教授。刘 杰，男，1979年生。湖南大学机械运载工程学院副教授、博士研究生导师。曾 侠，男，1993年生。湖南大学机械与运载工程学院本科生。唐应时，男，1946年生。湖南大学汽车车身先进设计制造国家重点实验室教授。