精密钢球传动减速机构的瞬时接触热特性分析

孙鹏飞 安子军 刘向辉

燕山大学机械工程学院,秦皇岛,066004

精密钢球传动减速机构的瞬时接触热特性分析

孙鹏飞 安子军 刘向辉

燕山大学机械工程学院,秦皇岛,066004

基于Hertz接触理论，以精密钢球传动减速机构为研究对象，建立了减速机构啮合副齿面接触分析模型。分析了钢球与摆线槽齿面间的瞬时接触域，在此基础之上，分析输入轴转速、负载对减速机构热特性的影响，得到钢球与齿面间接触域的瞬时生热率和瞬时摩擦温升。分析结果表明：钢球与摆线槽齿面的瞬时接触域是时变接触椭圆；输入轴转速和负载对瞬时生热率和瞬时摩擦温升都有明显影响，但转速的影响更大；瞬时摩擦温升在常规转速下随转速单调递增，在超低转速下随转速先递减再递增。研究结果为精密钢球传动的三维热力耦合分析奠定了理论基础。

精密钢球传动；瞬时接触域；生热率；摩擦温升

0 引言

精密钢球传动是一种新型端面啮合行星传动机构，该机构在内外摆线封闭槽之间放置若干钢球作为中介体传递运动和动力，因其具有无回差、传动比范围大等特点，在精密机械传动领域具有良好的应用前景。

随着高精密机械的发展，具有无回差传动特性的精密钢球传动逐渐成为研究热点。TERADA等[1-3]对这种传动机构进行了理论研究，并将成果应用于精密机械伺服传动机构。安子军等[4-8]对精密钢球传动的啮合理论、运动学、力学及动力学等进行了深入研究，取得了一系列研究成果。高东强等[9]针对二级摆线钢球减速器进行了结构设计，并运用Pro/E和ADAMS对其进行联合仿真分析，得到偏心盘和输出盘的角速度曲线。HIROYUKI等[10]定性分析了传动机构的钢球滚滑现象对输出轴转角误差的影响。聂松辉等[11]利用质心运动定理建立机构在有无配重两种情况下的运动微分方程，对机构的振动特性进行了研究。

目前关于精密钢球传动瞬时接触热特性的研究相对较少。本文以精密钢球传动减速机构为研究对象，运用Hertz接触理论，对钢球与摆线槽齿面间的瞬时接触域进行分析，获取瞬时接触域的几何特性参数；在此基础之上，运用BLOK[12]和ARCHARD[13]在摩擦温升方面的研究成果，对接触域的瞬时生热及瞬时摩擦温升进行研究，从理论上分析生热率及摩擦温升的变化规律，为精密钢球传动三维热力耦合分析提供理论基础。

1 结构和传动原理

精密钢球传动结构如图1所示。固定中心盘左端面上加工有齿数为z1的外摆线封闭槽；弱刚性组合行星盘右端面加工有齿数为z2的内摆线封闭槽。行星盘左端面和输出盘右端面上分别加工一组互相平行的锥形槽；在浮动盘左右两端面上各加工一组互相平行的锥形槽，并保证两端面对应位置的锥形槽互相垂直，右端面锥形槽和行星盘上的相同，左端面锥形槽和输出盘上的相同。固定中心盘、弱刚性组合行星盘和钢球4组成精密钢球传动的减速机构；弱刚性组合行星盘、浮动盘、输出盘和钢球6、8组成浮动盘式等速输出机构。

1.偏心输入轴 2.固定中心盘 3.弱刚性组合行星盘 4、6、8.钢球 5.壳体 7.浮动盘 9.输出轴(盘)图1 精密钢球传动结构图Fig.1 Structure diagram of precision ball transmission

偏心输入轴匀速转动，带动组合行星盘做行星运动，行星盘右端面的内摆线封闭槽推动钢球4运动。钢球4受到固定中心盘左端面上外摆线封闭槽的约束，反推行星盘以较低的角速度自转。行星盘的自转角速度经浮动盘式等速输出机构由输出轴(盘)输出，从而完成速度转换。

2 齿面接触模型

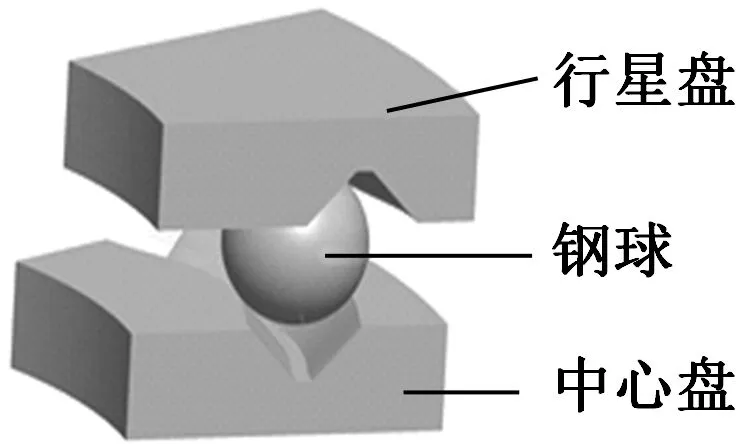
图2 减速机构单齿 啮合模型Fig.2 Single tooth meshing model of reducing mechanism

考虑到减速机构啮合副的对称性和啮合传动周期性[5]，当钢球系转过2π角度时，钢球系相对中心盘和行星盘分别转过一个齿[7]，故仅截取中心盘(外摆线)、行星盘(内摆线)上的一个齿进行分析。图2所示为减速机构单齿啮合模型。

假设钢球与齿面间接触为弹性接触，接触域法向压力分布不受滚动或滑动影响。减速机构在过啮合点的截面内，任意啮合位置的Hertz齿面接触模型如图3所示。钢球与外摆线槽齿面、内摆线槽齿面在啮合点处的局部坐标系分别为A1x1y1、A2x2y2(假设在某啮合位置A1、A2啮合点为传力接触，B1、B2啮合点为非传力接触[6])。

图3 Hertz齿面接触模型Fig.3 Hertz contact model of tooth surface

3 数学模型

3.1 瞬时接触域

在精密钢球传动减速机构中，钢球与摆线槽齿面间接触属于光滑非协调表面接触。根据Hertz接触理论可知，在法向载荷作用下，光滑非协调接触表面的瞬时接触域在接触点处的公切平面呈椭圆形。定义接触椭圆沿摆线槽齿面母线方向的半轴为椭圆半轴b，在接触面内垂直于齿面母线方向上的半轴为椭圆半轴a。

钢球与齿面的瞬时接触椭圆不仅受法向载荷N(φ)影响，同时还受到齿面主曲率κij的影响。N(φ)和κij均随着啮合位置变化，造成钢球与齿面间瞬时接触椭圆是时变接触椭圆。为了便于研究，假设从行星盘一侧看输入轴为逆时针转动。此时时变接触椭圆的几何特性为

(1)

(2)

(3)

Sij(φ)=πaij(φ)bij(φ)

(4)

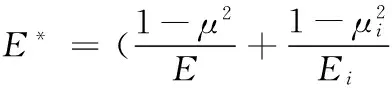
时变接触椭圆上的最大接触压力为

p0ij(φ)=

(5)

时变接触椭圆上法向压力分布为

(6)

式(1)、式(2)、式(5)中的F(e)是与钢球和摆线槽齿面在啮合点处主曲率有关的椭圆积分函数，当κij≥0时，有

当κij<0时，有

K(e)是第一类完全椭圆积分，E(e)是第二类完全椭圆积分。

3.2 接触热特性

精密钢球传动减速机构中生热的主要原因是各个钢球与齿面间的滑动摩擦。在任意啮合位置钢球与齿面间的啮合副摩擦生热计算公式[12]为

Hi(φ)=∬υi(φ)pi(φ)Vi(φ)dS

(7)

钢球与齿面间的相对滑动引起接触域摩擦温升，齿面上时变接触椭圆中心瞬时摩擦温升[13]为

(8)

本文假设钢球与齿面间摩擦功全部转化为啮合副摩擦热，摩擦热全部用于加热钢球与齿面。

4 瞬时接触热特性分析

文中计算范例所选取的减速机构设计参数为：中心盘齿数z1=13，行星盘齿数z2=15，短幅系数K=0.3，发生圆半径r0=3 mm，啮合钢球半径r=3 mm，摆线槽深3 mm，槽型角β=45°，槽底宽1 mm。样机材料为轴承钢GCr15。

(a)中心盘

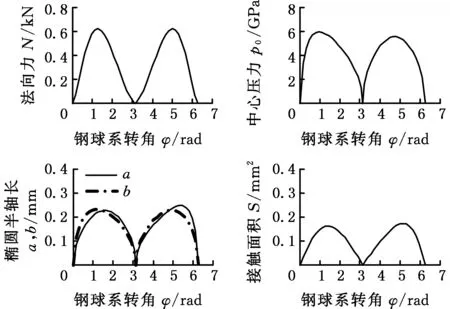
(b)行星盘图4 时变接触椭圆特性Fig.4 Characteristic of time-varying contact ellipse

减速机构在一个啮合周期内输入轴转速ωh=150 rad/s、负载Mr=38 kN·mm时，钢球与齿面瞬时接触域的时变接触椭圆特性如图4所示。由图4可知，在中心盘或行星盘上，前半周期和后半周期的各参数曲线，除了法向接触载荷曲线是关于φ=π对称分布，其余均不对称。其原因是在前半个周期内，钢球与中心盘摆线槽外侧和行星盘摆线槽内侧齿面相啮合；在后半个周期内，钢球则与中心盘摆线槽内侧和行星盘摆线槽外侧齿面啮合，摆线槽内外侧齿面上在关于φ=π对称的两个啮合点的主曲率不同。以半轴b观察时变接触椭圆的时变性，由图4可知，半轴b随钢球系转角在齿面上的变化形式为：长半轴—短半轴—长半轴—短半轴。时变椭圆以这种形式交替变化是因为齿面在实际啮合点处与齿面母线垂直方向上的主曲率κij按图5变化，一个周期内主曲率κij值的正负在交替变化。

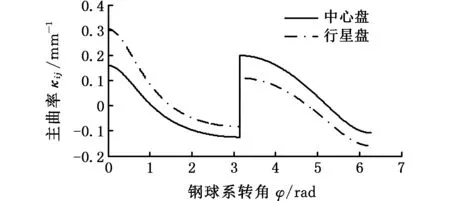
图5 摆线槽齿面啮合点主曲率κijFig.5 Main curvature of meshing point of cycloidal groove

由图4中S-φ曲线可知，摆线槽齿面上瞬时接触域非常小，中心盘和行星盘齿面上时变椭圆半轴的最大值约为0.25 mm，面积最大值约为0.18 mm2，在法向载荷N(φ)作用下，分布在接触域上的压力会比较大。由于同时受齿面曲率和法向接触载荷的影响，在摆线槽齿面上，最大时变椭圆未出现在椭圆半轴a、b相等时的位置或法向接触载荷最大时的位置，而是略有偏移，在钢球与摆线槽外侧齿面啮合时这种现象更为明显。

在摆线槽齿面上，法向接触载荷最大时的位置并不是时变椭圆中心压力最大时的啮合位置，而是位于其左侧。这是因为接触中心压力不仅受法向接触载荷的影响，同时还受瞬时接触域面积的影响。

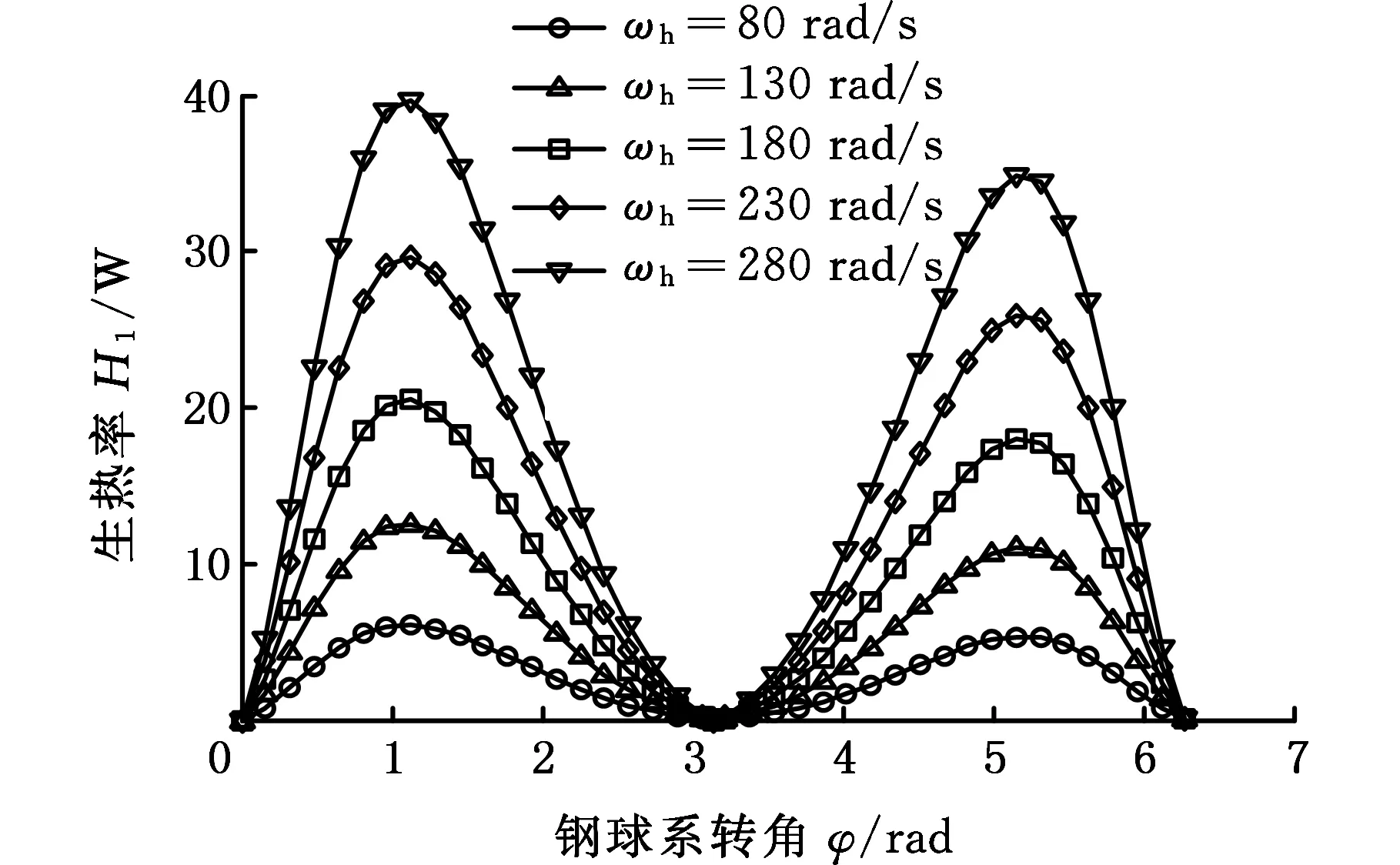
减速机构在一个啮合周期内负载Mr=38 kN·mm时，输入轴转速的变化对啮合副生热的影响如图6所示。由图6可知，各啮合位置的生热都随转速的升高而增大。其中，钢球与外侧齿面啮合时，生热率要高于钢球与内侧齿面相应位置啮合时的生热率，尤其是在靠近齿顶(图6中φ=0或φ=2π)约1/3齿高位置生热率相差最大，并且内外侧齿面上对应位置的生热率差值随着转速的升高而变大。这主要是由于钢球与外侧齿面啮合时，相对滑动速率和滑动摩擦因数比钢球与内侧齿面啮合时对应位置的滑动速率和摩擦因数要大，并且随着转速的升高，外侧齿面滑动速率和摩擦因数的增幅更大。图7为输入轴转速ωh由130 rad/s增大到180 rad/s时的相对滑动速率增幅ΔV和滑动摩擦因数Δυ增幅曲线。在图7中关于φ=π对称的位置，外侧齿面上的滑动速率增幅ΔV1和摩擦因数增幅Δυ1比内侧齿面上的滑动速率增幅ΔV2和摩擦因数增幅Δυ2大。

(a)中心盘

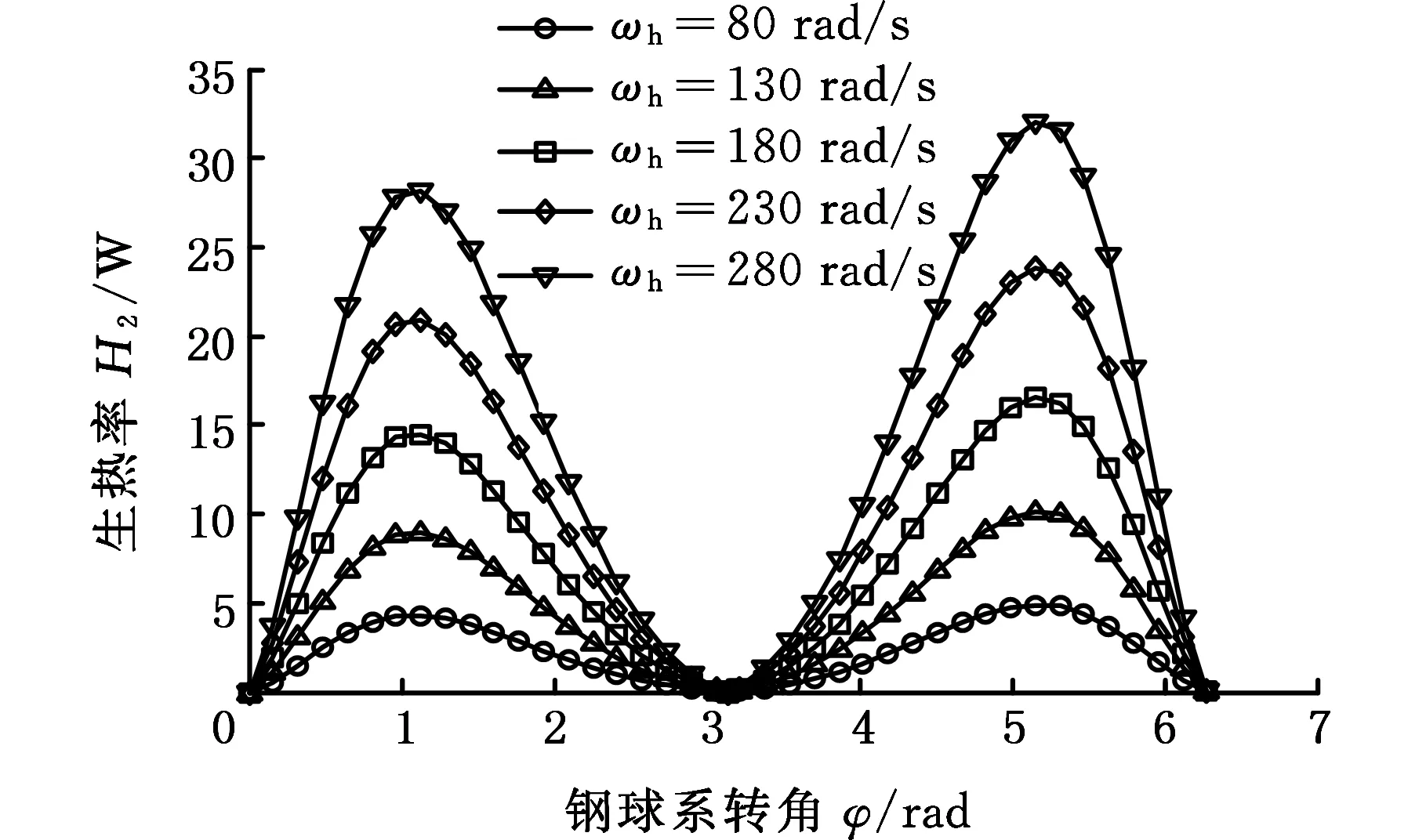
(b)行星盘图6 不同转速啮合副生热率变化Fig.6 Variation of heat generation rate of meshing pairs under different rotational speeds

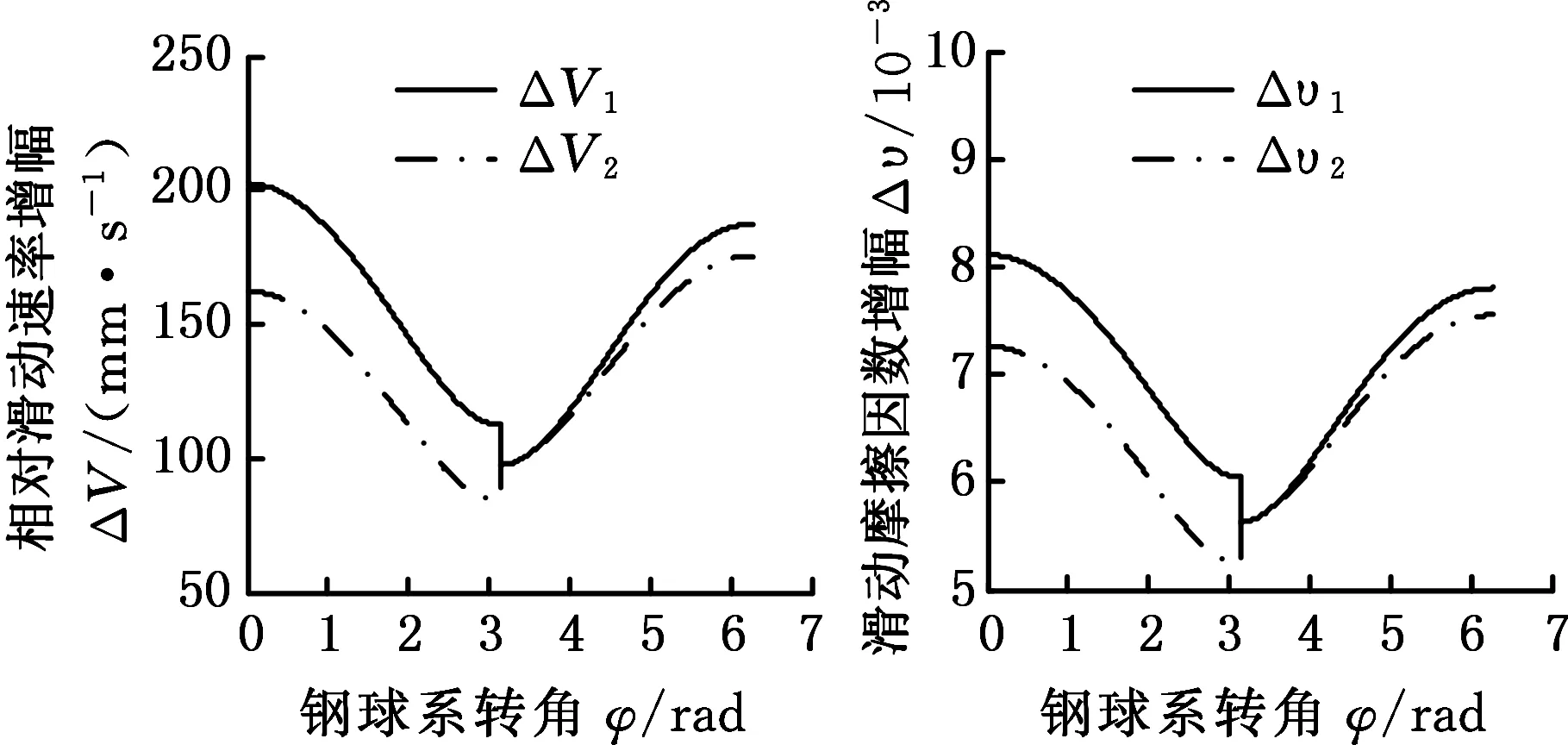
(a)相对滑动速率增幅(b)摩擦因数增幅图7 相对滑动速率增幅及摩擦因数增幅Fig.7 Relative sliding rateamplification and friction coefficient amplification

减速机构在一个啮合周期内输入轴转速ωh=150 rad/s时，在不同负载作用下啮合副生热变化情况如图8所示。由图8可知，这种工况下啮合副生热率的变化特征与图5所示的特征相似，随着负载的增大，生热率也在逐渐变大，不同之处在于负载引起生热率变化的幅度要小于输入轴转速引起生热率变化的幅度，这反映出啮合副生热率对输入轴转速的变化比对负载的变化更敏感。

(a)中心盘

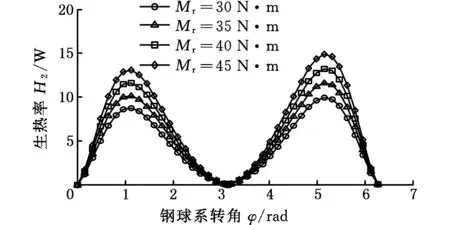
(b)行星盘图8 不同负载对啮合副生热率影响Fig.8 Influence of different loads on heat generation rate

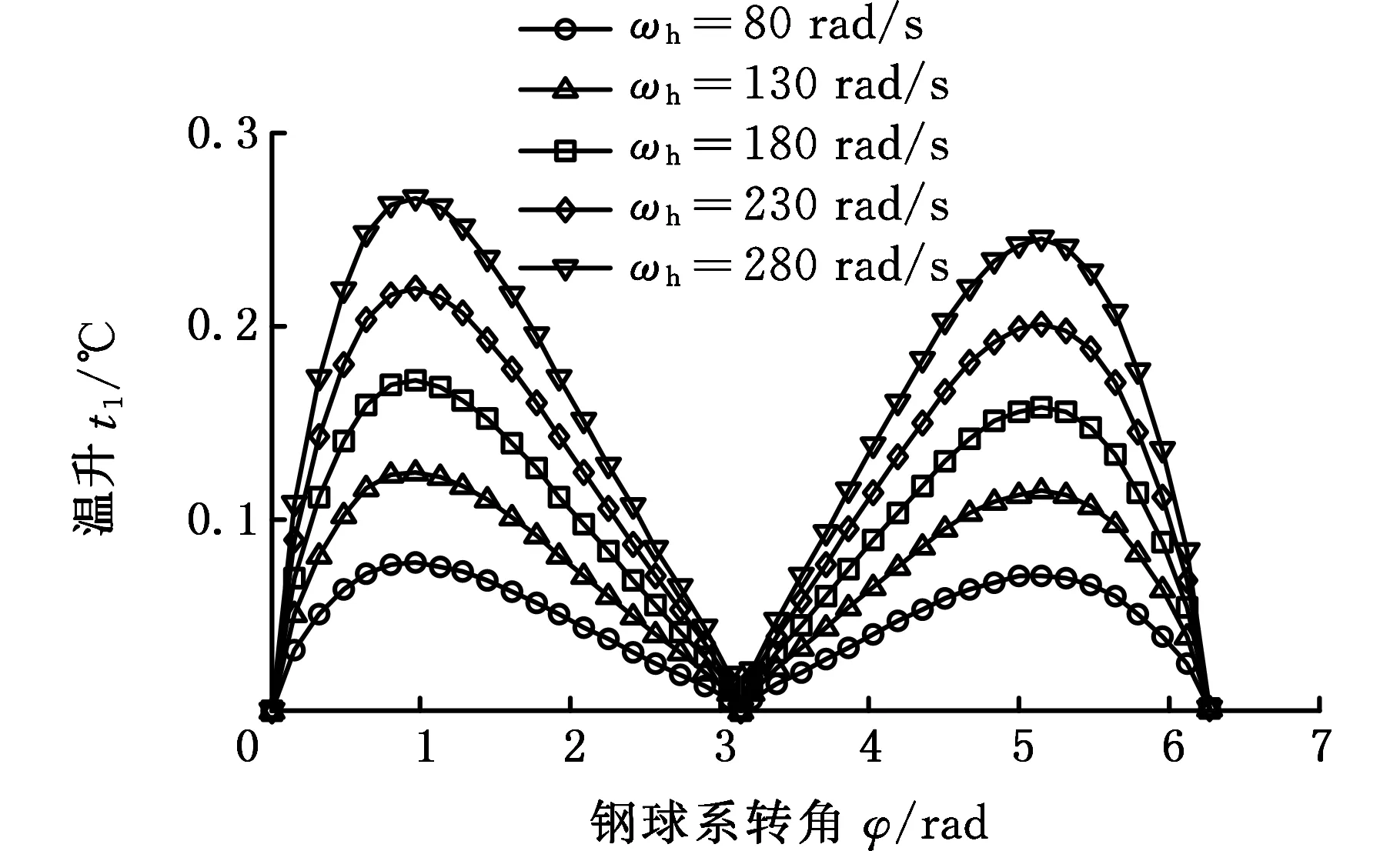
(a)中心盘

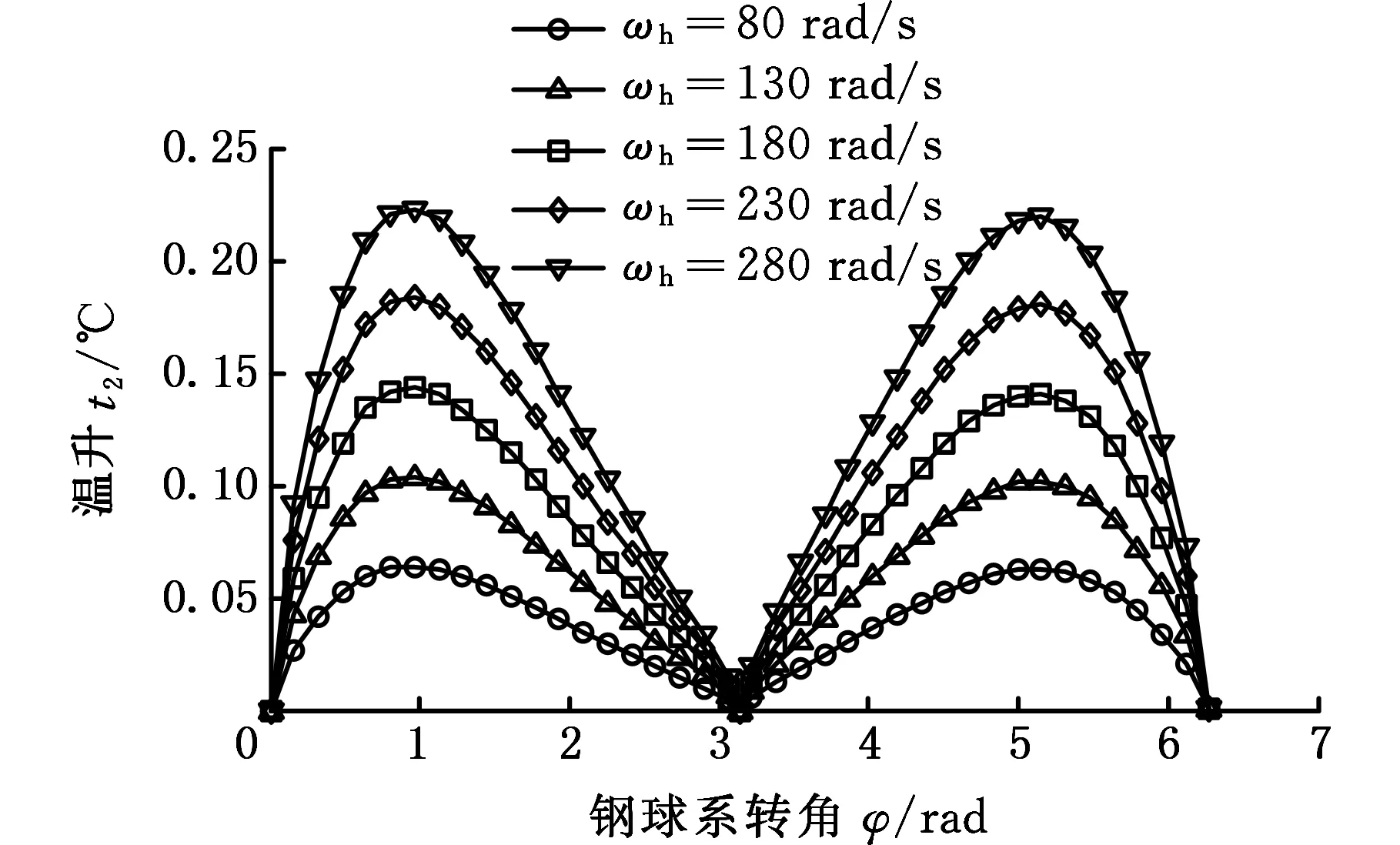
(b)行星盘图9 常规转速工况下时变接触椭圆中心瞬时温升Fig.9 Center instantaneous temperature rise of time-varying contact ellipse under conventional speed condition

输入轴转速对时变接触椭圆瞬时摩擦温升的影响需要分成两种情况分别进行讨论。

图9所示为一个啮合周期内常规输入轴转速变化引起的时变接触椭圆中心瞬时摩擦温升的变化情况。由图9可知，瞬时摩擦温升随着输入轴转速单调递增。在中心盘摩擦温升曲线上，关于φ=π对称的两个位置，外侧齿面大升高于内侧齿面温升，这与中心盘齿面上的生热变化相符；在行星盘摩擦温升曲线上，关于φ=π对称的两个位置，内侧齿面温升略大于外侧齿面温升，与行星盘齿面上的啮合副生热率曲线不符。这主要是因为任一啮合位置的摩擦温升受到此位置的曲率、法向接触载荷、相对滑动速率等多因素的综合影响。由于在靠近齿顶位置的曲率、滑动速率、摩擦因数比靠近齿根(φ=π)位置的大，因此靠近齿顶位置的温升增幅大于靠近齿根位置的温升增幅。

一个啮合周期内，在超低转速工况下，不同转速对时变接触椭圆中心瞬时摩擦温升的影响如图10所示。该工况下瞬时温升曲线特征与常规转速工况下的温升特征不同。从图10中各转速下的瞬时温升曲线可知：同一啮合位置，在某一转速范围内，瞬时摩擦温升随转速的升高而下降；过临界转速后，瞬时摩擦温升随着转速升高而升高。针对温升随转速先递减再递增的现象，图11给出了合理解释。图11所示为齿面滑动摩擦因数随输入轴转速的变化关系，从图11中可知，本文采用的Buckingham摩擦因数随着输入轴转速的升高先迅速下降再逐渐升高。结合式(7)和式(8)，便可解释超低转速工况下出现这一现象的原因。若采用其他摩擦因数计算公式，只要υ不取为常数(实际摩擦因数不可能为常数)，传动机构在低

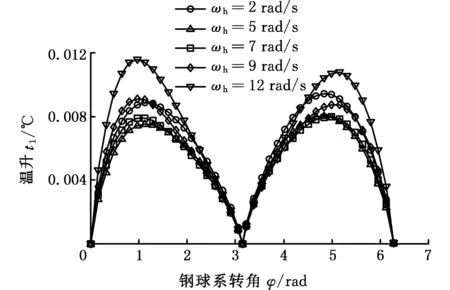
(a)中心盘

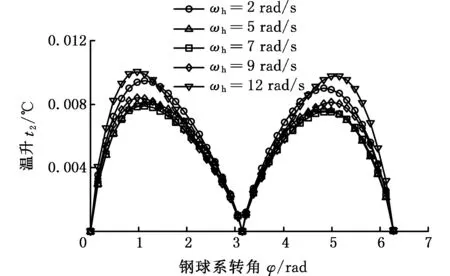
(b)行星盘图10 超低转速工况下时变接触椭圆中心瞬时温升Fig.10 Center instantaneous temperature rise of time-varying contact ellipse under ultralow speed condition

速区运转时总会有一最佳转速使各啮合位置的瞬时温升处于最小值。当机构处于低速或怠速工况时，减速机构的这一特性有利于减小因温度升高对传动装置造成的不利影响。

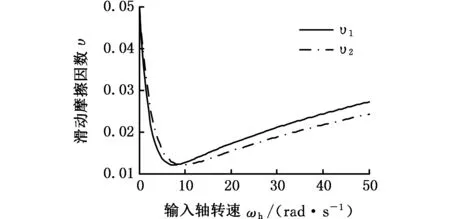
图 rad时υ-ωh关系Fig.11 Relation between υ and ωh at rad

在一个啮合周期内不同负载对时变接触椭圆中心瞬时摩擦温升的影响如图12所示。这种条件下瞬时温升曲线特征与常规转速工况下瞬时温升曲线特征相似。从图12中可看出，在同一啮合位置，不同负载引起的相邻两温升曲线的增幅和图9中转速导致的相邻两温升曲线增幅相比，负载引起的温升增幅较小，负载每增加5 N·m温升最大增幅约为0.01 ℃，这说明负载对瞬时摩擦温升的影响小于输入轴转速对瞬时摩擦温升的影响。

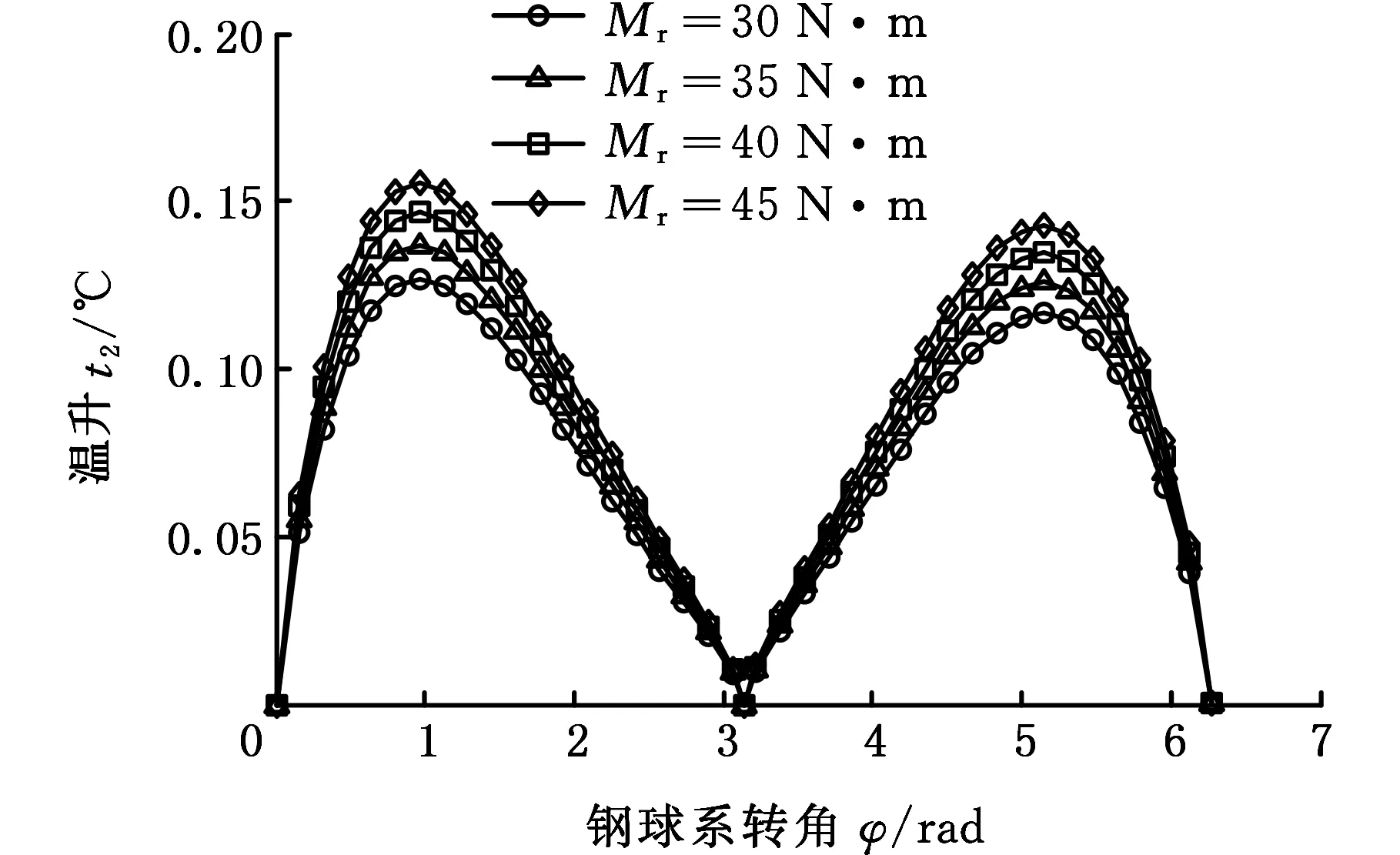
(a)中心盘

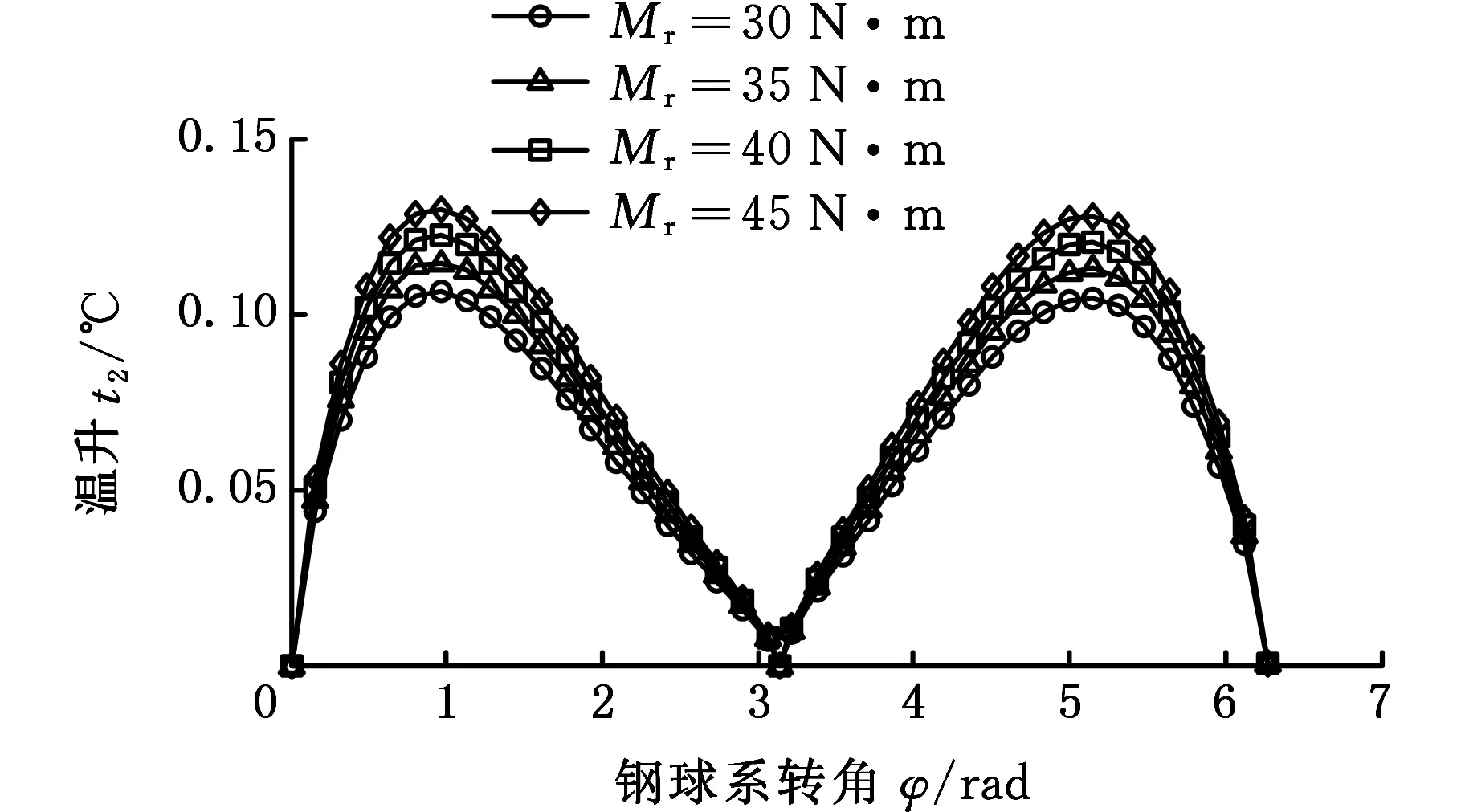
(b)行星盘图12 不同负载对时变接触椭圆中心瞬时温升影响Fig.12 Influence of different loads on center instantaneous temperature rise of time-varying contact ellipse

5 算例分析

取不同于前述分析的减速啮合机构设计参数：z1=10,z2=12,K=0.35，r0=3.5 mm,r=3.5 mm，β=45°，材料为GCr15。分析输入轴转速、负载对啮合副生热率及瞬时摩擦温升的影响。按前述分析模型，分别计算得到φ=π/3rad时啮合副生热率对输入轴转速和负载的变化率如图13所示，以及φ=π/3rad时啮合副瞬时摩擦温升对输入轴转速和负载的变化率如图14所示。图13的纵轴标目分别是生热率对转速、负载的变化率，图14的纵轴标目分别是温升对转速、负载的变化率。

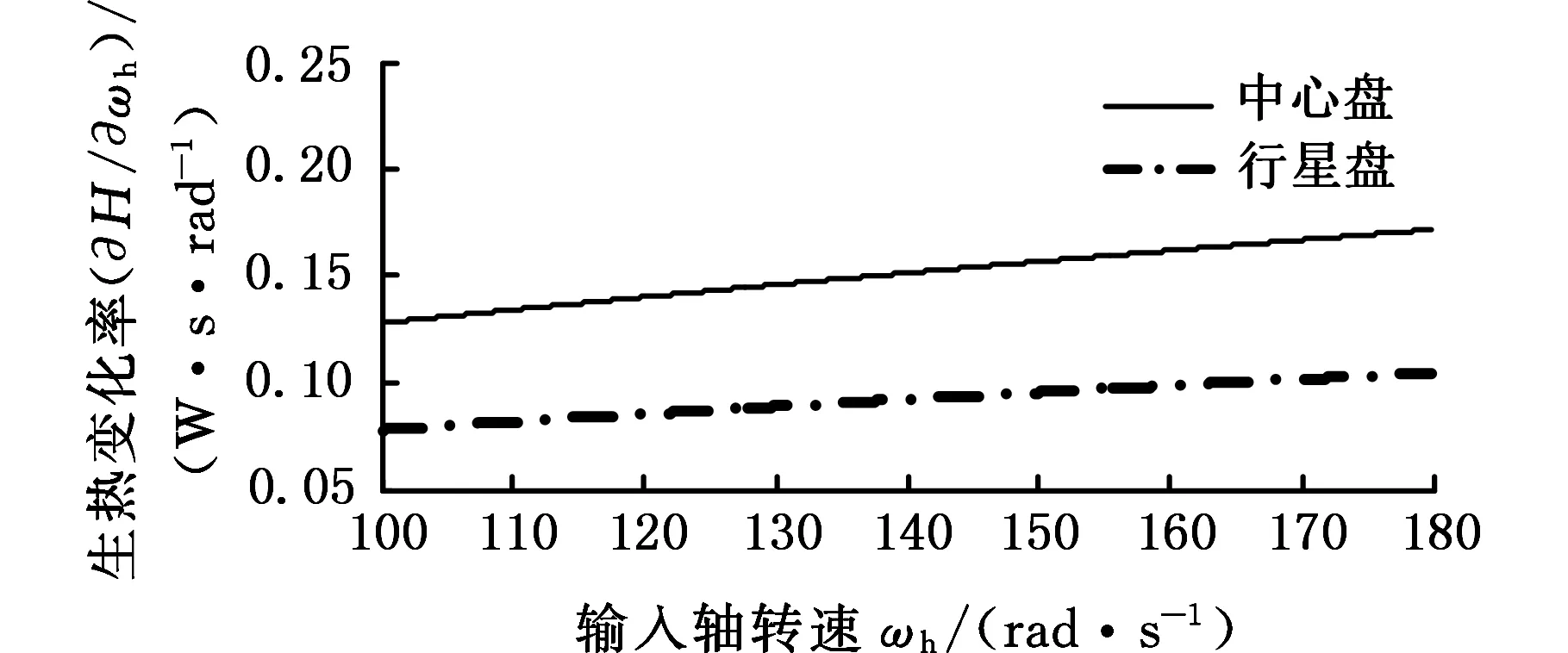
(a)生热率随转速的变化率

由图13和图14可知，啮合副生热率和瞬时摩擦温升对输入轴转速和负载的变化率均为正，表明生热率和瞬时摩擦温升随输入轴转速和负载的增大而增大，但增大的幅度有所不同。图13a中啮合副生热率对输入轴转速的变化率随转速增大而增大,可知，啮合副生热率的增幅随输入轴转速的增大而逐渐变大。比较图13a和图13b以及比较图14a和图14b可知，输入轴转速对生热率和瞬时摩擦温升的影响更显著。综合可见算例计算结果与前述分析结果是吻合的,证明了钢球与齿面间的瞬时接触热特性分析结果的正确性。

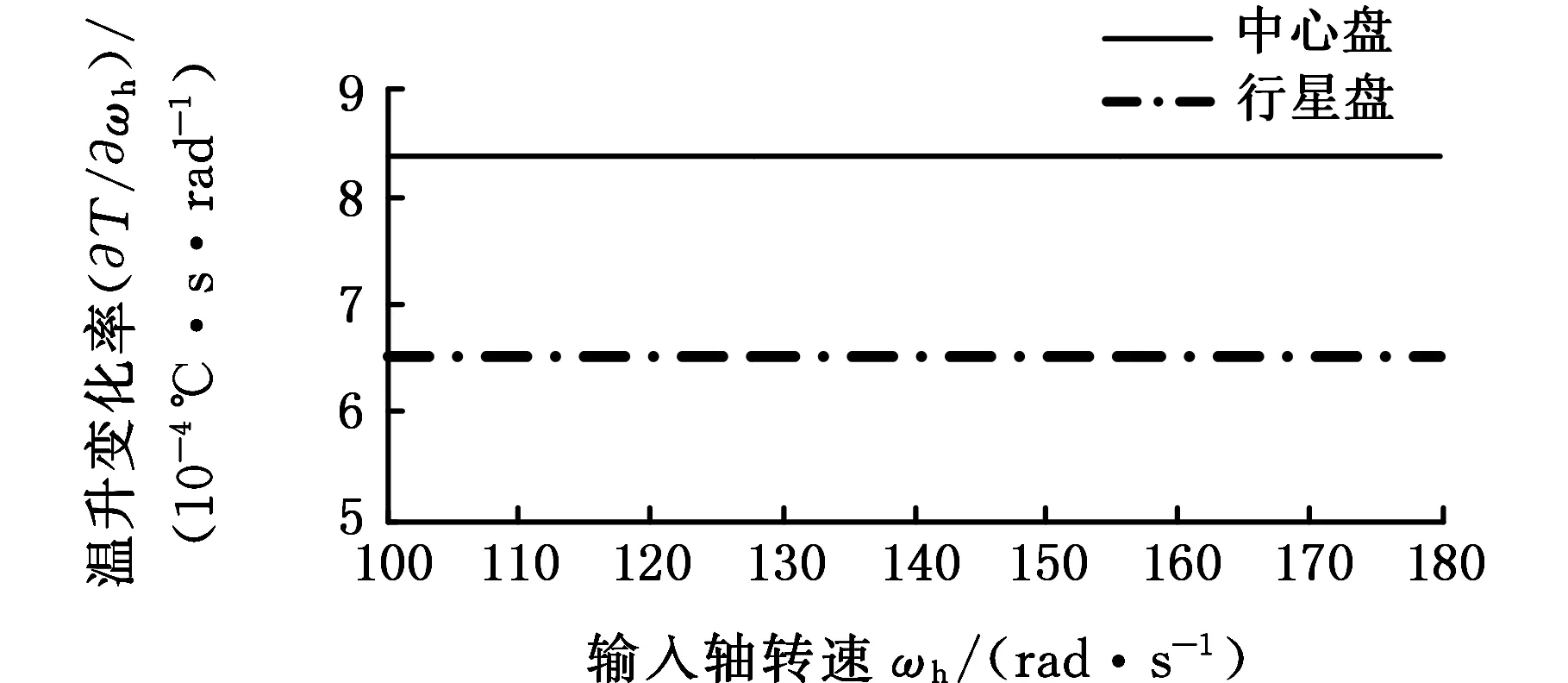
(a)瞬时温升随转速的变化率

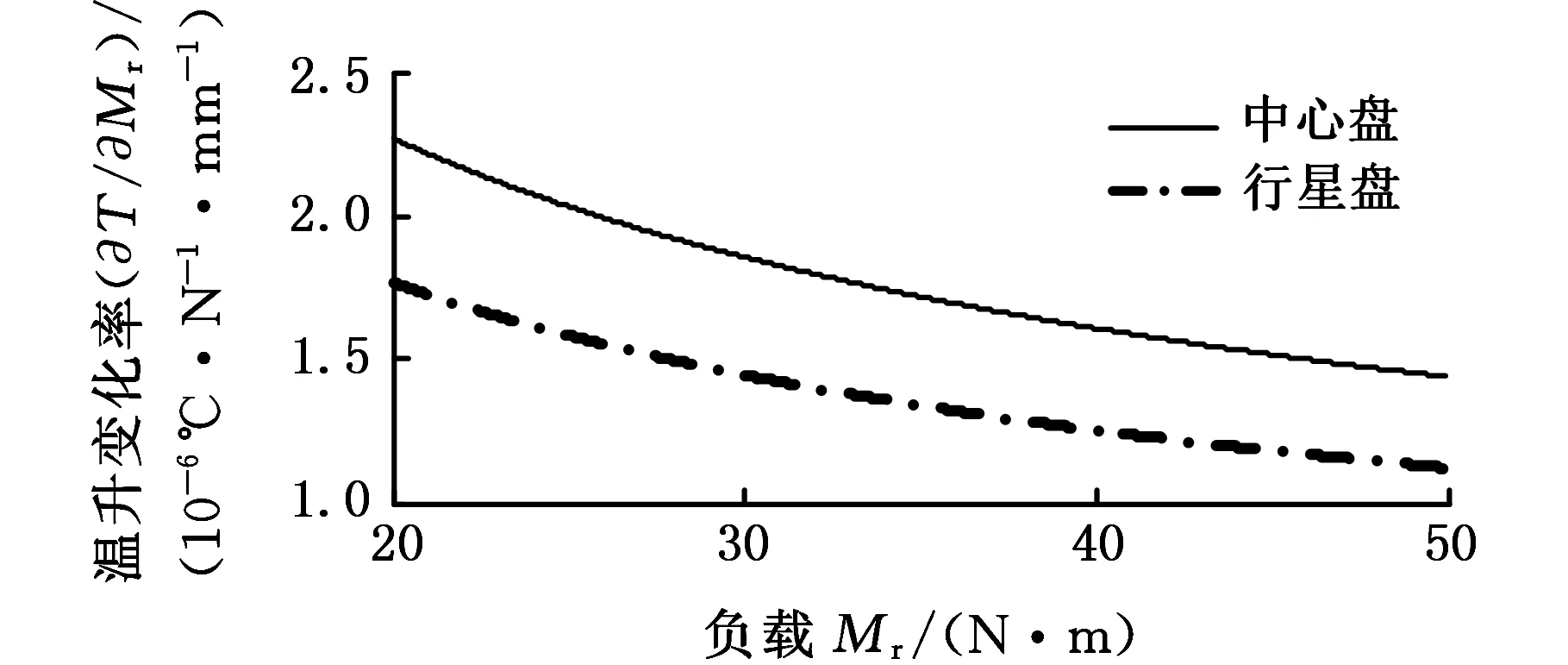
(b)瞬时温升随负载的变化率图14 瞬时温升随转速、负载的变化率Fig.14 Rate of instantaneous temperature rise varies with speed and load

6 结论

(1)基于Hertz接触理论建立齿面接触模型，推导出瞬时接触椭圆几何特性参数的公式，得知钢球与摆线槽齿面的瞬时接触域是时变接触椭圆。

(2)摆线槽齿面上同一啮合位置的瞬时生热率随着输入轴转速和负载的增大而增大，且生热率增幅随输入轴转速的增大逐渐变大；瞬时生热率对输入轴转速的变化更敏感；摆线槽外侧齿面的生热率高于内侧齿面的生热率。

(3)摆线槽齿面上同一啮合位置，常规转速的瞬时摩擦温升随输入轴转速单调递增；而超低转速的瞬时摩擦温升随着输入轴转速先递减再递增。瞬时摩擦温升随负载单调递增，它对转速的变化更敏感。啮合副的最大瞬时温升分别出现在中心盘外侧齿面和行星盘内侧齿面上。

[1]TERADAH，MAKINOH，IMASEK.FundamentalAnalysisofCycloidBallReducer(3rdReport)[J].JSPE，1995，61(12)：1075-1079.

[2]TERADAH，MAKINOH，IMASEK.FundamentalAnalysisofCycloidBallReducer(4thReport)[J].JSPE，1997，63(6)：834-838.

[3]TERADAH.TheDevelopmentofGearlessReducerswithRollingBalls[J].JournalofMechanicalScienceandTechnology, 2010，24(1)：189-195.

[4] 安子军，曲志刚，张荣贤. 摆线钢球传动齿形综合研究[J]. 机械工程学报，1996，32(5)：41-46.ANZijun，QUZhigang，ZHANGRongxian.ResearchonToothShapeSynthesisoftheCycloidBallTransmission[J].ChineseJournalofMechanicalEngineering，1996，32(5)：41-46.

[5] 张鹏，安子军，杨作梅. 摆线钢球行星传动啮合副非线性力学性能研究[J]. 工程力学，2010，27(3)：186-192.ZHANGPeng，ANZiJun，YANGZuomei.ResearchonNonlinearMechanicalPropertiesforEngagementPairofCycloidBallPlanetaryTransmission[J].EngineeringMechanics，2010，27(3)：186-192.

[6] 安子军. 摆线钢球行星传动研究[D]. 秦皇岛：燕山大学，2000.ANZiJun.TheResearchforCycloidSteelBallPlanetaryTransmission[D].Qinhuangdao：YanshanUniversity，2000.

[7] 宜亚丽，安子军，王海侠. 无隙钢球精密传动啮合副滑动特性研究[J]. 中国机械工程，2014，25(23)：3206-3211.YIYali，ANZijun，WANGHaixia.SlidingPropertyResearchonMeshingPairofNo-backlashBallPrecisionTransmission[J].ChinaMechanicalEngineering，2014，25(23)：3206-3211.

[8] 张鹏，安子军. 摆线钢球行星传动动力学建模与固有特性分析[J]. 中国机械工程，2014，25(2)：157-162.ZHANGPeng，ANZijun.DynamicsModelandNaturalCharacteristicsofCycloidBallPlanetaryTransmission[J].ChinaMechanicalEngineering，2014，25(2)：157-162.

[9] 高东强，王伟. 摆线钢球行星传动机构设计与仿真分析[J].陕西科技大学学报，2014，32(6)：139-150.GAODongqiang，WANGWei.TheStructuralDesignandSimulationAnalysisoftheCycloidBallPlanetaryTransmissionMechanism[J].JournalofShanxiUniversityofScience&Technology，2014，32(6)：139-150.

[10]HIROYUKIO，YUSUKEM，HIROSHIN.BehaviorofBallsinaStandardBallReducer[J].ProceedingsoftheJapanSocietyofMechanicalEngineers，2002，674(68)：290-296.

[11] 聂松辉，李鸿，颜彧.摆线钢球减速器振动分析[J].机械设计与研究，2014，30(2)：56-58.NIESonghui，LIHong，YANYu.TheVibrationAnalysisoftheCycloidSteelBallReducer[J].MachineDesignandResearch，2014，30(2)：56-58.

[12]BLOKH.TheFlashTemperatureConcept[J].Wear，1963，6(6)：483-494.

[13]ARCHARDJF.TheTemperatureofRubbingSurfaces[J].Wear，1958，2(6)：438-455.

(编辑 苏卫国)

Analysis on Instantaneous Contact Thermal Characteristics of Reducing Mechanisms for Precision Ball Transmissions

SUN Pengfei AN Zijun LIU Xianghui

School of Mechanical Engineering，Yanshan University，Qinhuangdao，Hebei,066004

Based on the Hertz contact theory, a tooth surface contact model was established forward to analyze the instantaneous contact areas and thermal characteristics of reducing mechanisms for precision ball transmissions. The contact patches among the balls and tooth surfaces of cycloidal groove were analyzed, then the effects of the input shaft speeds and loads on the thermal characteristics of reducing mechanisms were investigated. Instantaneous heat generation rates and instantaneous frictional temperature rises among the balls and tooth surfaces were obtained. The results indicate that the instantaneous contact areas among the balls and tooth surfaces of cycloid groove is a time-varying contact ellipse. The input shaft speeds and loads have visible influences on instantaneous heat generation rates and frictional temperature rises, but the influences of speeds are greater. Instantaneous friction temperature rises are monotonically increasing with the increased speeds under the general speed conditions, but in the low speeds, temperature rises are monotonically decreased and then monotonically increased. The results of the study provide a good foundation for three dimensional thermal mechanical coupling analyses of precision ball transmissions.

precision ball transmission; instantaneous contact area; heat generation rate; friction temperature rise

2016-05-16

国家自然科学基金资助项目(51275440)；河北省自然科学基金资助项目(E2013203085)

TH132.4

10.3969/j.issn.1004-132X.2017.09.001

孙鹏飞，男，1990年生。燕山大学机械工程学院博士士研究生。研究方向为精密机械传动理论与控制技术。E-mail：ysupfsun@sina.com。安子军(通信作者)，男，1960年生。燕山大学机械工程学院教授、博士研究生导师。E-mail:zjan@ysu.edu.cn。刘向辉，男，1992年生。燕山大学机械工程学院硕士研究生。