一维斜向超声振动辅助磨削滚动轴承钢工艺及试验研究

王 艳 王 帅 刘建国 李德蔺

上海理工大学机械工程学院，上海,200093

一维斜向超声振动辅助磨削滚动轴承钢工艺及试验研究

王 艳 王 帅 刘建国 李德蔺

上海理工大学机械工程学院，上海,200093

针对目前只有一维轴向、一维切向等振动方向不变的一维超声振动辅助磨削的情况，首次提出了一维斜向超声振动辅助磨削工艺方法。利用MATLAB对一维斜向超声振动辅助磨削磨粒的运动轨迹进行了模拟分析。建立了超声振动试验系统的动力学模型。通过对超声振动工作台的模态分析,研制了一维斜向超声振动辅助磨削试验系统，对不同角度下超声振动辅助磨削滚动轴承钢的磨削力及表面粗糙度值进行了研究，探究了磨削力及表面粗糙度值随超声振动方向的变化规律。多次试验结果表明，超声振动角度为67.5°附近的表面粗糙度值明显优于其他角度的表面粗糙度值，磨削力也有减小。对正交试验结果的极差分析得出：当超声振动角度为67.5°、砂轮速度为20 m/s、工件速度为0.5 m/min以及磨削深度为4 μm时，加工后的工件表面粗糙度达到最低值，其中工件速度是影响表面粗糙度的最重要工艺参数。

斜向；超声振动辅助磨削；动力学模型；磨削力；表面粗糙度

0 引言

超声振动辅助磨削是将超声频率的机械振动附加到砂轮或者工件上的一种复合磨削加工技术。国内外学者对超声振动辅助磨削进行了大量研究。郎献军[1]建立了轴向超声振动辅助磨削45钢的磨削力模型，对轴向超声振动能够减小磨削力进行了理论验证。张洪丽等[2]对一维切向超声振动辅助磨削的试验表明：施加切向超声振动时，磨削力及磨削力比均减小，能够改善硬脆材料的可加工性。SPUR等[3]对径向超声振动辅助磨削陶瓷材料的研究中发现：超声振动辅助磨削能使磨削力减小，工件去除率提高。闫艳燕[4]设计了在切向、轴向同时施加超声振动的二维磨削装置，明显提高了磨削纳米复相陶瓷的表面质量。TAGHI等[5]对超声振动辅助磨削42CrMo4进行了研究，结果表明,与传统磨削相比，施加超声振动能使磨削法向力减小约60%，而且磨削温度降低显著。NIK等[6]自行设计并经过优化分析，研制了轴向超声振动辅助磨削试验装置，对Ti6Al4V合金进行研究发现，与普通磨削相比，法向磨削力及切向磨削力平均减小约13.5%和14.2%，并且表面粗糙度减小了10%。ABDULLAH等[7]对超声振动辅助磨削和普通磨削铝合金、X210Cr12钢的磨削力及表面粗糙度值做了对比试验研究，发现干磨时，超声振动辅助磨削的磨削力及表面质量都要优于普通磨削，超声振动辅助磨削没有出现磨削烧伤和表面毛刺现象。 MAHADDALKAR等[8]对超声振动辅助磨削的磨削力及磨削温度做了研究，发现超声振动使磨削力明显减小，通过建立热源模型进行仿真及试验得出，超声振动使流入工件的热流减少约42%，大大减小了发生磨削烧伤的可能性。

诸多学者的研究大多集中于一维轴向或一维切向超声振动，而二维超声振动的装置设计也比较复杂。本文提出了一种新型的一维斜向超声振动辅助磨削工艺，该工艺融合了一维轴向与一维切向超声振动的优势，用自行设计的一维斜向超声振动辅助磨削系统，通过改变超声振动方向与机床坐标系之间相对角度的一系列正交试验，对磨削滚动轴承钢时的磨削力及表面粗糙度值进行了研究。

1 斜向超声振动辅助磨削的运动学分析

超声振动辅助磨削是将超声振动与普通磨削结合起来的一种加工方法，与普通磨削相比，超声振动辅助磨削时砂轮表面磨粒相对于工件的运动方式有所不同，导致磨削要素也会发生变化。本节将建立一维斜向超声振动辅助磨削时磨粒运动的数学模型，并用MATLAB进行仿真分析，研究超声振动时磨粒运动轨迹对材料去除方式的影响。

为研究方便，将坐标系oxy固定在工件上。普通磨削时磨粒的运动包括两部分：绕砂轮轴线以线速度vs的圆周运动，相对于工件沿x方向以速度vw的匀速平移运动。图1所示为普通磨削及超声振动辅助磨削的运动方式。

(a)普通磨削(b)轴向超声振动辅助磨削

(c)切向超声振动(d)斜向超声振动 辅助磨削 辅助磨削图1 普通磨削和超声振动辅助磨削的运动方式Fig.1 The motion modes of traditional grinding and ultrasonic vibration assisted grinding

一维斜向超声振动辅助磨削的超声振动方向与砂轮轴向在平行于工件表面的平面内可以形成0～90°夹角，通过自行设计的一维斜向超声振动辅助磨削系统可以实现一维轴向或切向超声振动无法实现的效果。

磨粒的运动除绕砂轮轴线的圆周运动和沿x方向的匀速平移运动外，还有一个沿超声振动方向的简谐振动(幅值为A，频率为f)，超声振动方向与砂轮轴向的夹角为α。假设坐标原点与主轴轴线重合，且处于砂轮中心，振动初相位为0。将超声振动投影到砂轮轴向和切向，即可推导出一维斜向超声振动辅助磨削时砂轮磨粒相对于工件的运动方程[9]：

(1)

ω0=2πfωs=2vs/ds

式中,t为时间;ω0为超声振动角频率;ds为砂轮直径;ωs为砂轮角速度。

取A=10 μm，f=19.98 kHz，ds=300 mm，vs=15 m/s，vw=1 m/min，α=67.5°代入式(1)中，即可模拟出超声振动方向与砂轮轴向成67.5°时的单颗磨粒三维运动轨迹，如图2中曲线1所示。令参数f=0，其他参数不变，可得到相同工况下普通磨削时单颗磨粒的运动轨迹，如图2中曲线2所示。图2作图时将振幅A放大了10倍。

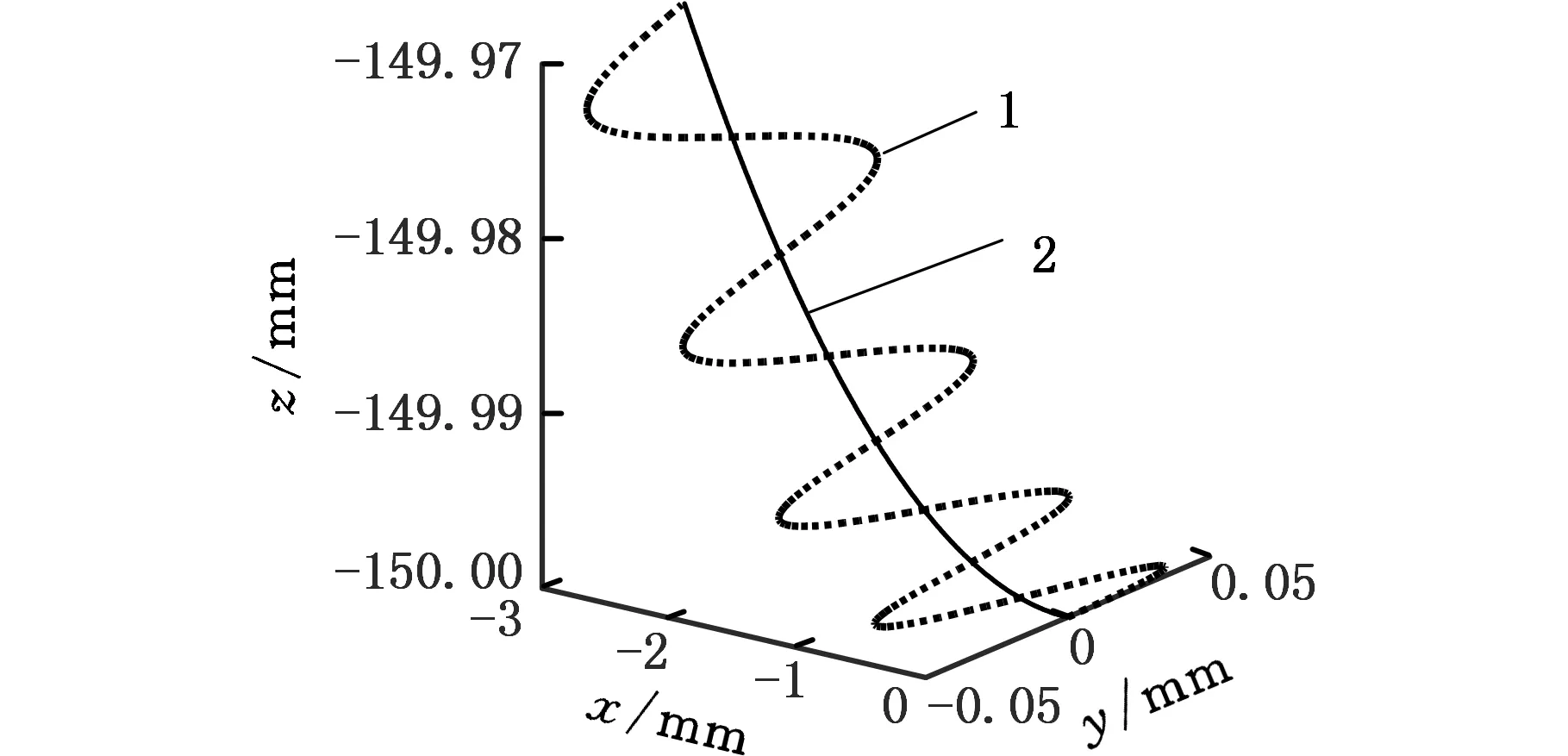
(a)α=67.5°时三维视角下的两种轨迹

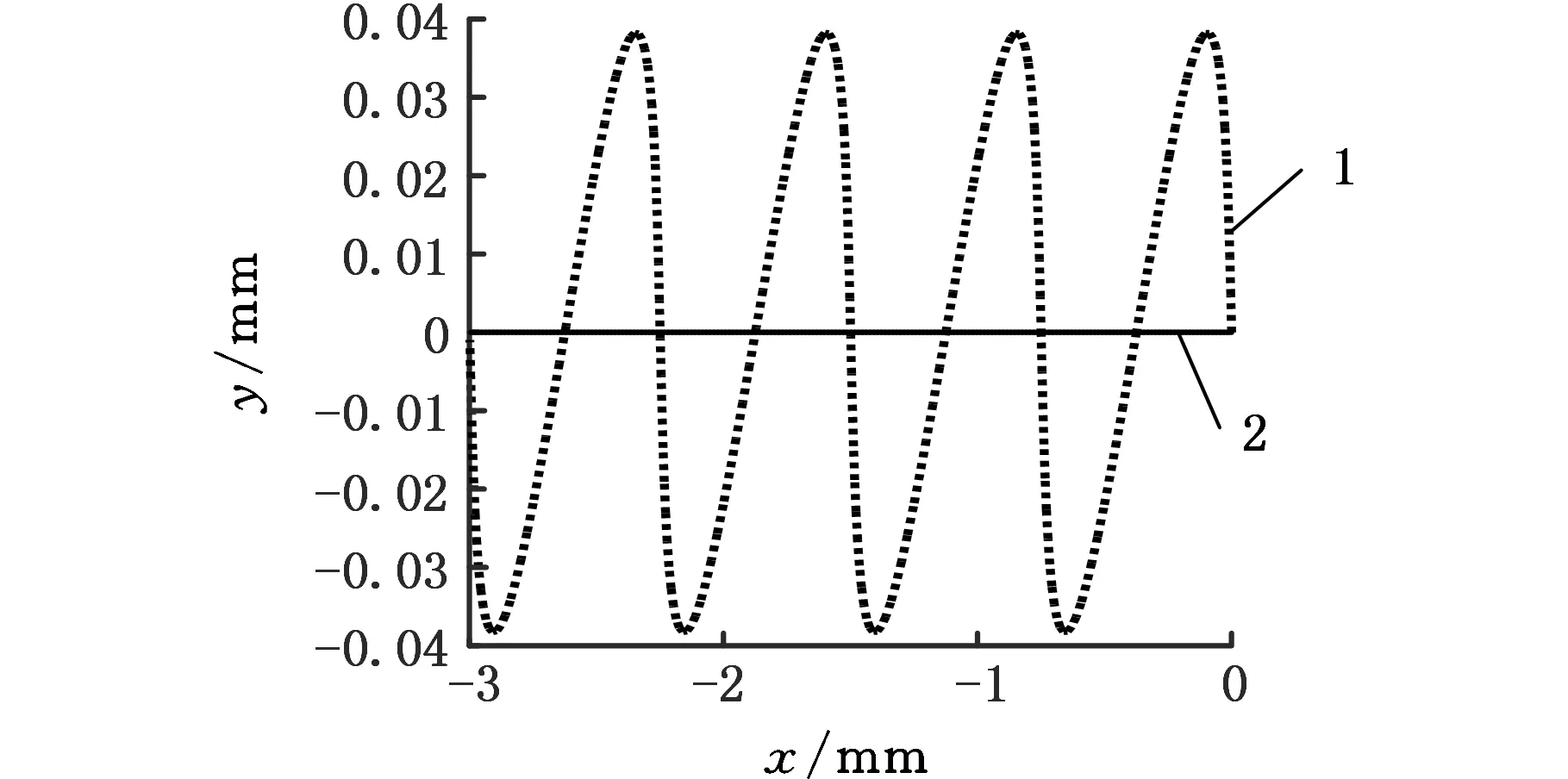
(b)α=67.5°时oxy平面内两种轨迹投影

(c)α=67.5°时oxz平面内两种轨迹投影 1.超声振动轨迹 2.普通磨削轨迹图2 一维斜向超声振动辅助磨削磨粒运动轨迹 与普通磨削磨粒轨迹Fig.2 The motion paths of particle for oblique ultrasonic vibration grinding and traditional grinding

从图2中可以看出，一维斜向超声振动可以看作是一个一维轴向超声振动和一个一维切向超声振动的合成运动，它兼顾了轴向超声振动辅助磨削时单颗磨粒几何接触弧长变长、磨削轨迹变宽的优势特性，以及一维切向超声振动辅助磨削时磨粒多次往复熨压的优势特性。

2 一维斜向超声振动系统分析

2.1 一维斜向超声振动试验系统的动力学模型

本试验中的超声振动辅助磨削系统由超声波发生器、超声振动系统(声学部件)、磨削机床及相应的检测设备如测力仪、动平衡检测系统等部分组成。超声振动系统的结构简图见图3。工件托台通过双头螺柱与阶梯形变幅杆相连，变幅杆与换能器经过阻抗匹配后安装在一起。试验时，超声振动电源产生高频电信号传递给换能器。换能器将电能转化为纵向超声机械振动Asin(ω0t+φ0)，其中A是换能器端部的超声振动振幅，ω0是超声激励角频率，φ0是超声振动初相位。通过变幅杆与工件托台将振动传递到工件安装位置，从而使工件产生符合工况要求的超声振动。超声振动的传递依靠的是变幅杆与工件托台内部各个质点的纵向振动，而工件托台和变幅杆的实际外形也近似由数段杆状体组成，因而可以把变幅杆和工件托台的振动问题简化为杆状连续体的纵向振动问题。

图3 超声振动系统结构简图Fig.3 Structure of ultrasonic vibration system

试验中超声振动系统的动力学模型如图4所示。图中工件托台简化为两段等截面杆1和2。杆1、2之间是工件托台的支承位置，该支承简化为一刚度为k的弹性约束。阶梯形变幅杆简化为两段等截面杆3和4。杆1，2，3，4分别采用独立的坐标系x1～x4。其中Ai为杆i的截面积，Li为杆i的长度，Ei为杆i的弹性模量，ρi为杆i的密度(i=1，2，3，4)。工件托台为铝合金材料，变幅杆为钢材。显然A1=A2，E1=E2，ρ1=ρ2，E3=E4，ρ3=ρ4。杆i中任一位置的位移响应分别为ui，各段杆的振动方程如下[10]：

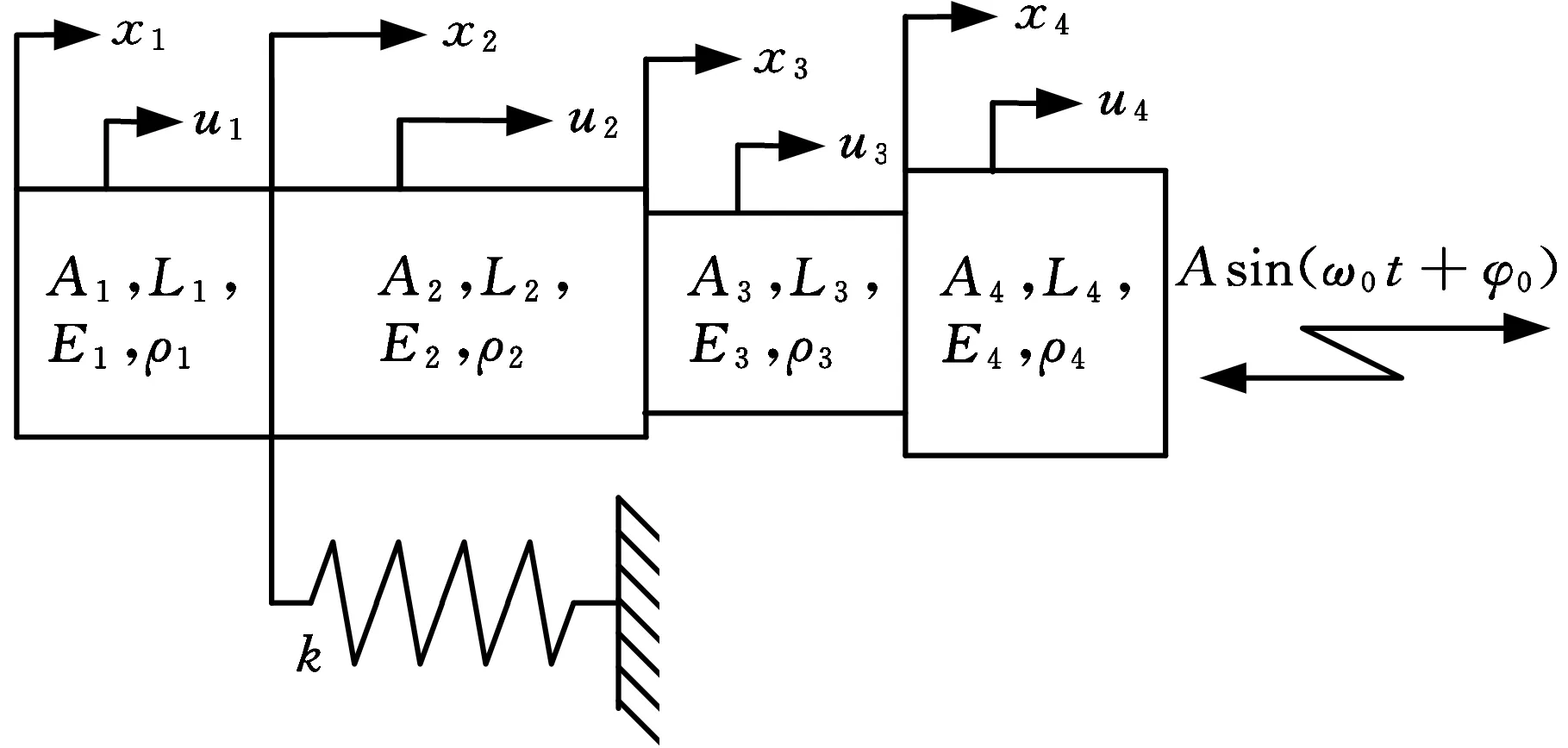
图4 试验中超声振动系统动力学模型Fig.4 Dynamic model of ultrasonic vibration system

(2)

式中，Ci、Di为待定系数；ω为系统固有角频率；φ为由初始条件决定的振动相位。

对于该模型，可以提出以下边界条件与连续条件：

(1)边界条件1。杆1左端为自由端，应力为零，即当x1=0时，有

(2)边界条件2。杆4的右端为自由端，应力为零，即当x4=L4时，有

(3)连续条件1。杆1、2相连处位移与内力相等，即当x1=L1，x2=0时，有

(4)连续条件2。杆2、3相连处位移与内力相等，即当x2=L2，x3=0时，有

(5)连续条件3。杆3、4相连处位移与内力相等，即当x3=L3，x4=0时，有

将式(2)分别代入上述条件中，最终可以得到系统频率方程：

(3)

式中，k为杆1和杆2相连处弹性支承的刚度。

式(3)是一个超越方程，不能直接给出ω的表达式，但当给出E、A、L、ρ等参数的具体值后可以用数值方法求得各阶固有角频率ωj(j=1,2,…)的近似值，将ωj代入式(2)即可得到各段杆的振型方程。当外加超声振动激励角频率ω0≈ωj时，上述振动系统会接近共振状态。

2.2 试验中超声振动工件托台的模态分析及结构优化

波的物理实质是能量传送的过程。超声波是一种纵波，能传递很强的能量，超声波在弹性介质的传播过程中任意横截面的总能量不变，而振幅与能量密度成正比[11]，即

式中，K′为系数。

在超声振动工件托台的设计时，一般考虑将工件托台的长度尺寸定为工作台中超声波的半波长，或者定为超声波波长的整数倍，此时工件托台末端放工件的位置将达到最大振幅。超声波波长λ可由下式求得：

(4)

(5)

其中，vu为超声波在超声振动工件托台中的传播速度，m/s；f为超声波在工件托台中振动的频率，Hz。本装置超声振动工件托台选用航空铝材T7075，密度ρ=2.81 g/cm3，泊松比μ=0.33，弹性模量E=71 GPa。

将上述材料参数代入式(4)、式(5)，经过计算求得超声波在T7075中的波长λ=252 mm，这里取半波长作为参考尺寸来确定振动工件托台的长度，用ANSYS Workbench进行模态分析并优化后得到工件托台的长度为124.4 mm、宽度为56 mm、高度为32 mm。由于超声振动变幅杆的共振频率范围为19.6～20.3 kHz，因此对超声振动试验装置进行模态分析时，需要满足两个设计要求[6]：一是工件托台与变幅杆装配后，能够在该频率范围内达到共振状态，二是提取的该阶共振状态的模态为纵向振型。图5所示为提取的纵向振动的模态分析，其频率为19.83 kHz，在与变幅杆共振的频率范围内，可以认为该设计方案满足试验要求。

图5 超声振动工作台模态分析Fig.5 Modal analysis of ultrasonic vibration workbench

一维斜向超声振动试验的方案主要依靠自行设计的一维斜向超声振动试验装置来实现，它可实现超声振动方向与砂轮轴向的夹角在0～90°变化。该装置主要由同心定位的两个圆盘形旋转部分组成，其下半部分固定在Kistler-9257B 压电陶瓷式三向测力仪上，超声振动工件托台连接在上半部分，这样就能保证超声振动工件托台旋转而测力仪不动，确保任意角度变化时测量的都是砂轮轴向、径向和切向三个方向的力。

3 试验条件及试验结果分析

3.1 一维斜向超声磨削试验条件

磨削试验工件选用优质轴承钢GCr15，磨削前需进行热处理：850°淬火，200°低温回火。其化学成分见表1。

表1 GCr15化学成分(质量分数)Tab.1 Chemical composition of GCr15(mass fraction) %

该磨削试验是在斯莱福林KP-48T光学玻璃精密磨床上进行的，该磨床的砂轮转速范围为5～30m/s。砂轮的选择对磨削加工十分重要，直接影响着磨削工件的表面质量、磨削力、磨削温度与砂轮的损耗等。工件选用轴承钢GCr15，硬度较高，综合各方面因素，试验选用树脂结合剂200目CBN砂轮。在试验开始之前，先将工件加工成15mm×12mm×5mm尺寸。磨削工艺参数设定如下:砂轮速度为10m/s，15m/s，20m/s；磨削深度为4μm，6μm，8μm；工件速度为0.5m/min，1m/min，1.5m/min。磨削的条件为一次行程(逆磨、干磨)，试验的工装系统如图6所示。

图6 斜向超声振动辅助磨削试验系统Fig.6 Experimental system of oblique ultrasonic vibration assisted grinding

试验时，将工件粘贴在工件托台端部上方中间区域。由于超声振动装置加工误差及工件本身误差的存在，在砂轮一次行程中工件表面不能完全被磨到，因此需要先将工件表面磨平。为了减少不必要的影响因素，每次试验前都用金刚石笔对砂轮做一次修整，使砂轮达到相同的工况。修整参数：修整深度10μm，轴向进给速度50μm/r，砂轮速度vs=10 m/s。

3.2 普通磨削试验测量结果

首先对工件做一组普通磨削试验，磨削参数设置如表2所示。

表2 磨削参数Tab.2 Grinding parameters

为了降低误差对结果的影响，取三次试验的平均值，测量所用表面粗糙度仪为Taylor Hobson Form Talysurf 200b，沿垂直于磨削方向进行测量，取样长度为5 mm。测量试验结果如表3所示。

表3 普通磨削试验结果Tab.3 The result of traditional grinding

3.3 超声振动角度对磨削力及表面粗糙度值的影响

假定砂轮轴向为0方向，为了减少试验次数,取角度α分别为0、22.5°、45°、67.5°、90°进行试验。其他磨削参数设置同表2。Kistler测力仪测得的磨削力信号如图7所示。试验结果如表4所示。

(a)轴向磨削力

(b)切向磨削力

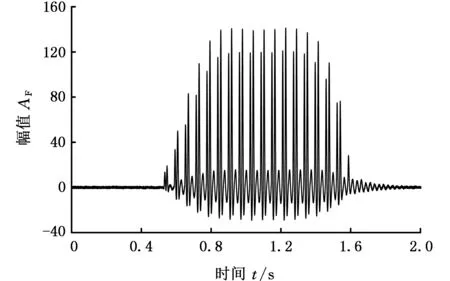
(c)法向磨削力图7 Kistler测力仪测得的磨削力信号(α=22.5°)Fig.7 Grinding force signal measured by Kistler (α=22.5°)表4 一维斜向超声振动辅助磨削时的试验结果Tab.4 The result of one dimensional oblique ultrasonic vibration assisted grinding

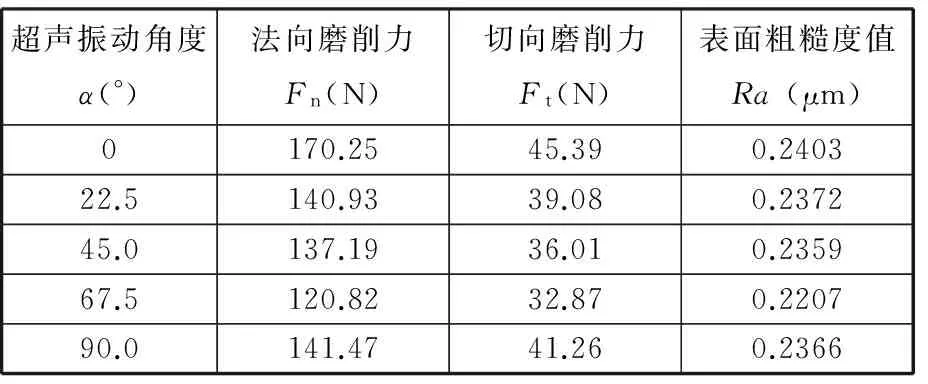
超声振动角度α(°)法向磨削力Fn(N)切向磨削力Ft(N)表面粗糙度值Ra(μm)0170.2545.390.240322.5140.9339.080.237245.0137.1936.010.235967.5120.8232.870.220790.0141.4741.260.2366

磨削力随角度变化的趋势如图8a所示，工件表面粗糙度值随角度变化的趋势如图8b所示。由图8a可知，不论角度如何变化，超声振动辅助磨削的磨削力都小于普通磨削时的磨削力，平均分别减小约32.1%和27.2%，表面粗糙度也优于普通磨削的表面粗糙度，表面粗糙度值减小约10.3%。

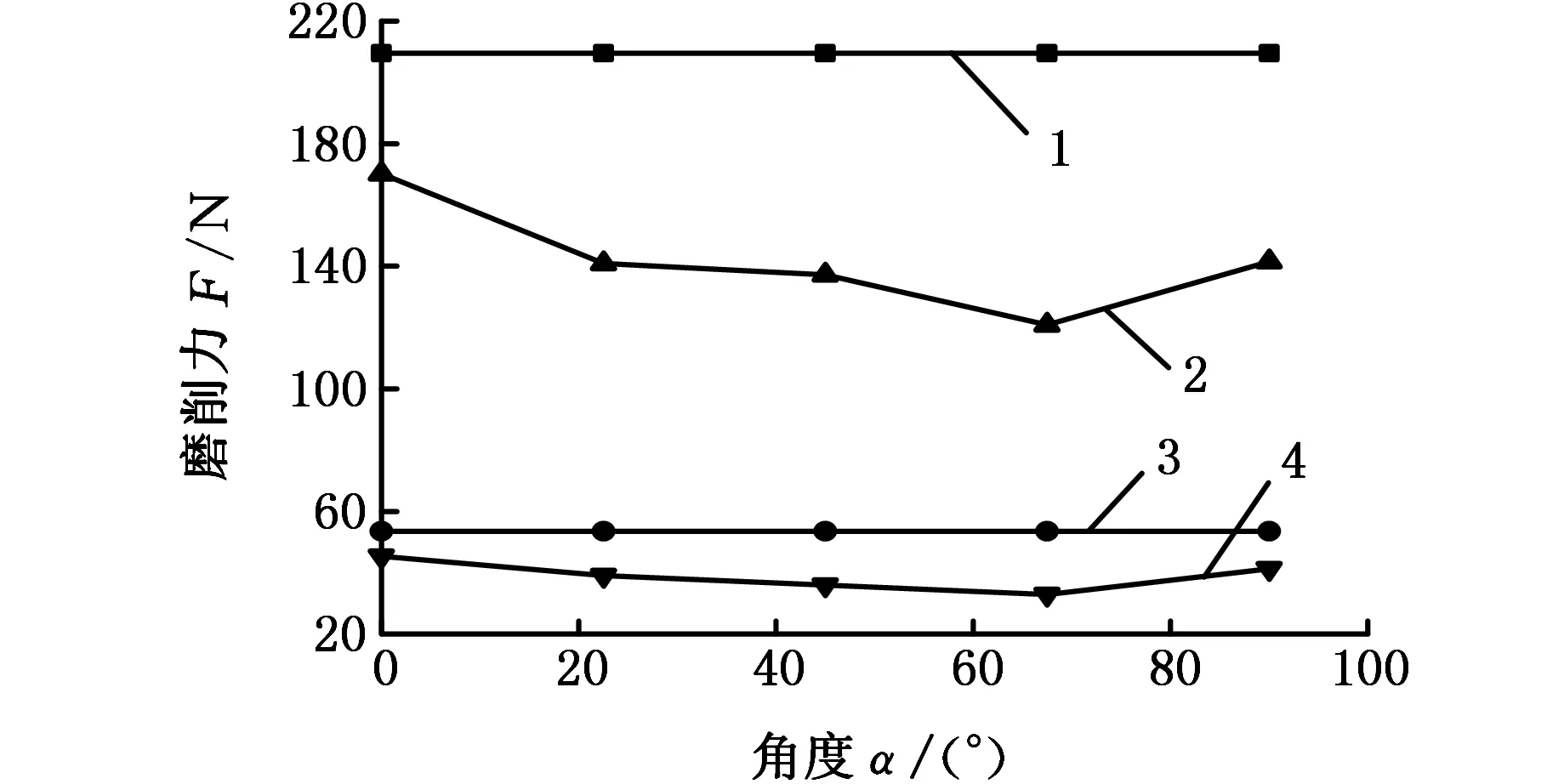
1.普通磨削Fn 2.超声磨削Fn3.普通磨削Ft 4.超声磨削Ft(a)磨削力随振动角度变化的趋势

1.普通磨削 2.超声磨削 (b)表面粗糙度值随振动角度变化的趋势图8 磨削力及表面粗糙度值随超声振动角度 变化的趋势Fig.8 Variation trend of the grinding force and surface roughness with the direction of ultrasonic vibration

由图8可以看出：超声振动角度在0～90°变化时，磨削力及表面粗糙度值也随之变化，在67.5°左右磨削力和表面粗糙度值最小，明显优于单纯的一维轴向或切向超声振动辅助磨削的加工效果，这说明一维斜向超声振动辅助磨削具有明显优势。将一维斜向超声振动辅助磨削的运动投影到砂轮轴向和砂轮切向，则在砂轮轴向和砂轮切向同时存在超声振动，在超声振动角度改变的同时，砂轮轴向和切向振动的振幅也随之变化，结果表明，磨削力及表面粗糙度值变化与轴向及切向超声振动的振幅密切相关。

斜向超声振动可以看成是由同频率同相位的轴向超声振动与切向超声振动的合成。无论是轴向超声振动还是切向超声振动都有减小磨削力和表面粗糙度的效果，这两种效果的显著程度都与超声振幅的大小成正相关[9,12]。在图8中，随着振动角度α在0～90°变化，工件的振幅并未发生变化，只是投影到轴向与切向的振幅分量大小有所改变。

假设工件振幅为x，则轴向振幅分量为xcosα，切向振幅分量为xsinα。当0<α<90°时，总有

xcosα+xsinα>x

即轴向振幅与切向振幅之和总大于工件振幅。这就是斜向超声振动辅助磨削比单纯的轴向或者切向超声振动辅助磨削效果更好的原因。

在α从0～90°变化的过程中，xcosα+xsinα-x的值先增大后减小，所以图8a中磨削力的变化趋势是先减小后增大，图8b中表面粗糙度值的变化趋势是先减小后增大。在图8的试验结果中最优角度为67.5°，这是由试验对象材料硬度较高所导致的。切向超声振动对磨削高硬度材料具有独特优势：切向超声振动可以使砂轮磨粒与工件发生周期分离，磨粒对工件材料产生冲击作用，促进了材料的去除，从而减小了加工高硬度工件时的磨削力和表面粗糙度值[9，13]。因此在本次试验中，切向超声振动的作用比轴向超声振动的作用更加显著。当超声振动角度为67.5°时，切向振幅分量大于轴向振幅分量，所以试验结果中的最优角度是67.5°。

3.4 正交试验的磨削力及表面粗糙度值分析

采用正交试验法(4因素3水平)研究不同磨削参数对工件表面粗糙度值的影响规律，表5为正交试验加工因素水平表，表6所示为试验结果。

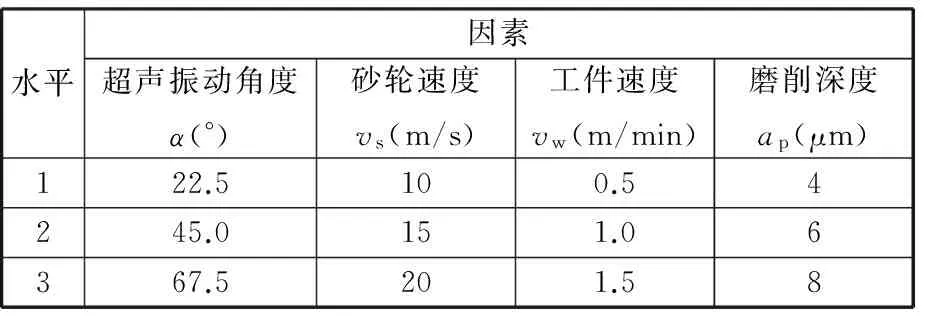
表5 因素水平表Tab.5 The factors and levels table

表6 正交试验结果Tab.6 The result of orthogonal experiment

极差分析法(简称“R”法)具有计算简便、直观形象、简单易懂等优点，是正交试验结果分析最常用的方法[14]，本文采用极差分析法对正交试验结果进行数据分析。编写MATLAB程序得到正交试验的极差分析结果如表7所示。

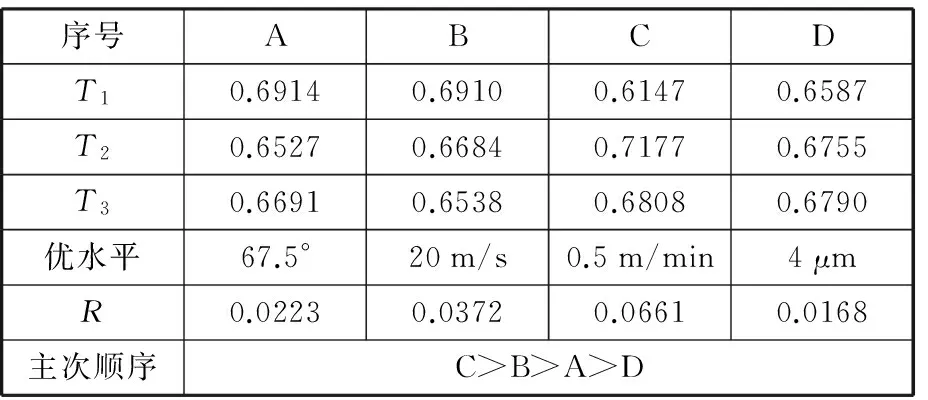
表7 极差分析结果表Tab.7 Range analysis results

表7中，A为超声振动角度，B为砂轮速度，C为工件速度，D为磨削深度；Ti为任一列上水平值为i时所对应的试验指标之和；R为极差，是任一列因素各水平的试验指标的最大值与最小值之差，即R=max(Ti)-min(Ti)，R反映了各列因素的水平变动时，试验指标的变动幅度。

因为各因素的优水平的确定与试验指标(表面粗糙度值)有关，由Ti的大小可以判断各因素的最优水平，此处表面粗糙度值越小越好，因此可以得出最优水平为：超声振动角度67.5°、砂轮速度20 m/s、工件速度0.5 m/min、磨削深度4 μm。R越大，说明该因素对试验指标的影响越大，因此也就越重要。从表7中可以看出，各因素对工件表面粗糙度值影响由大至小依次为：工件速度vw、砂轮速度vs、超声振动角度α、磨削深度ap。对最优磨削参数进行试验验证，最优磨削参数和磨削试验结果如表8所示。将表8中的磨削试验结果与表4、表6进行比较可以看出，当采用正交试验极差分析所得的最优参数磨削时的磨削力最小，表面粗糙度值最小。以上试验结论可作为超声振动辅助磨削滚动轴承钢的参数设定依据。

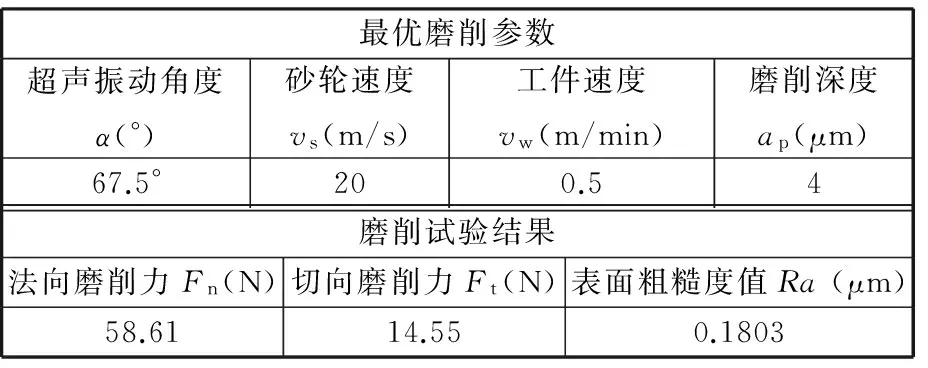
表8 最优磨削参数及磨削试验结果Tab.8 Optimal grinding parameters and results of grinding experiment

4 结论

(1)本文提出了一维斜向超声振动辅助磨削的概念，建立了一维斜向超声振动试验系统的动力学模型，设计了一维斜向超声振动辅助磨削试验系统，通过对试验装置的模态分析及优化改进，达到了试验要求。

(2)与普通磨削相比，超声振动辅助磨削的法向力和切向力都明显减小，分别平均减小约32.1%和27.2%。试验结果表明在不同角度的斜向超声振动下，67.5°左右的法向磨削力及切向磨削力的减小最明显，分别减小约42.3%和38.5%。

(3)与普通磨削相比，超声振动辅助磨削的表面粗糙度值有了改善，平均减小约10.3%，在超声振动角度变化过程中，67.5°角附近的表面粗糙度值改善最大，减小约14.6%。

(4)利用极差分析法对正交试验数据进行分析得出了使一维斜向超声振动辅助磨削滚动轴承钢表面粗糙度值最优时的磨削参数最优组合：超声振动角度为67.5°、砂轮速度为20 m/s、工件速度为0.5 m/min、磨削深度为4 μm，对指导实际的生产加工有重要意义。

[1] 郎献军. 轴向超声振动辅助磨削的磨削力建模研究[D]. 长沙:中南大学, 2014. LANG Xianjun. Study on Grinding Force Modeling of Axial Ultrasonic Vibration Assisted Grinding[D]. Changsha:Central South University, 2014.

[2] 张洪丽, 张建华. 切向超声振动辅助磨削对单颗粒切削力的影响[J]. 兵工学报, 2011, 32(4):487-492. ZHANG Hongli, ZHANG Jianhua. Effects of Tangential Ultrasonic Vibration on Grinding Force of Single Abrasive Grit[J]. Acta Armamentarii, 2011, 32(4):487-492.

[3] SPUR G, HOLL S E.Ultrasonic Assisted Grinding of Ceramics[J].Journal of Materials Processing Technology, 1996,62(4):287-293.

[4] 闫艳燕. 纳米复相陶瓷二维超声振动辅助磨削机理及其表面质量研究[D]. 上海:上海交通大学, 2008. YAN Yanyan. Study on Two Dimensional Ultrasonic Vibration Assisted Grinding Mechanism of Nanocomposite Ceramics and Its Surface Quality[D]. Shanghai:Shanghai Jiao Tong University, 2008.

[5] TAGHI T, BAHMAN A, MOHAMMAD R. Ultrasonic Assisted Dry Grinding of 42CrMo4[J]. International Journal of Advanced Manufacturing Technology, 2009, 42(9/10):883-891.

[6] NIK M G, MOVAHHEDY , AKBARI J. Ultrasonic-assisted Grinding of Ti6Al4V Alloy[J]. Procedia CIRP, 2012, 1(9):353-358.

[7] ABDULLAH A, SOTOODEZADEH M, ABEDINI R, et al. Experimental Study on Ultrasonic Use in Dry Creep-feed Up-grinding of Aluminum 7075 and Steel X210Cr12[J]. International Journal of Precision Engineering & Manufacturing, 2013, 14(2):191-198.

[8] MAHADDALKAR P M, MILLER M H. Force and Thermal Effects in Vibration-assisted Grinding[J]. International Journal of Advanced Manufacturing Technology, 2014, 71(5):1117-1122.

[9] 张洪丽. 超声振动辅助磨削技术及机理研究[D]. 济南:山东大学, 2007. ZHANG Hongli. Study on the Technology and Mechanism of Ultrasonic Vibration Assisted Grinding[D]. Jinan:Shandong University, 2007.

[10] 张义民. 机械振动[M]. 北京:清华大学出版社, 2007:175-177. ZHANG Yimin. Mechanical Vibration[M]. Beijing:Tsinghua University Press,2007:175-177.

[11] 顾鼎超. 超声变幅杆优化设计仿真及负载效应试验研究[D]. 南京:南京农业大学, 2011. GU Dingchao. Simulation of the Optimal Design of Ultrasonic Horn and Experimental Study for Load Effect[D]. Nanjing:Nanjing Agricultural University, 2011.

[12] 唐进元, 周伟华, 黄于林. 轴向超声振动辅助磨削的磨削力建模[J]. 机械工程学报, 2016, 52(15):184-191. TANG Jinyuan, ZHOU Weihua, HUANG Yulin. Modeling on Grinding Force Assisted with Axial Ultrasonic Vibration[J]. Journal of Mechanical Engineering, 2016,52(15):184-191.

[13] 张洪丽, 张建华. 超声振动磨削运动学分析[J]制造技术与机床, 2006(6):63-66. ZHANG Hongli, ZHANG Jianhua. Kinematics Analysis on Ultrasonic Vibration Grinding[J]. Manufacturing Technology & Machine Tool, 2006(6):63-66.

[14] 王岩, 隋思涟. 试验设计与MATLAB数据分析[M]. 北京:清华大学出版社, 2012.:159-162. WANG Yan, SUI Silian. Experimental Design and MATLAB Data Analysis[M]. Beijing:Tsinghua University Press,2012:159-162.

(编辑 王旻玥)

One Dimensional Oblique Ultrasonic Vibration Assisted Grinding for Rolling Bearing Steels and Experimental Validation

WANG Yan WANG Shuai LIU Jianguo LI Delin

School of Mechanical Engineering,University of Shanghai for Science and Technology,Shanghai，200093

Previous studies about one dimensional ultrasonic vibration assisted grinding were limited to fixed directions of ultrasonic vibration such as one dimensional axial or tangential vibration. A novel process of oblique ultrasonic vibration assisted grinding was presented. The motion paths of abrasive particles in oblique ultrasonic vibration assisted grinding were simulated in MATLAB. A dynamics model of experimental ultrasonic vibration system was established. Experimental devices of oblique ultrasonic vibration assisted grinding were designed through modal analysis of ultrasonic workbench. Grinding forces and surface roughnesses in grinding rolling bearing steels were studied at different directions of ultrasonic vibrations. The regulation of grinding forces and surface roughnesses with the direction of ultrasonic vibration was studied. Experimental results show that the best surface quality may be obtained when the angle of ultrasonic vibration is as 67.5° and grinding forces are also decreased. Results of orthogonal experiments demonstrate that ultrasonic vibration angle of 67.5°, wheel speed of 20 m/s, workpiece speed of 0.5 m/min, grinding depth of 4 μm are the optimum parameters to obtain the best surface quality of workpiece， and the speed of workpiece has the most important impacts on the surface quality of workpiece.

oblique; ultrasonic vibration assisted grinding; dynamics model; grinding force; surface roughness

2016-12-30

上海市研究生创新基金资助项目(JWCXSL1402)

TG580

10.3969/j.issn.1004-132X.2017.09.003

王 艳，女，1969 年生。上海理工大学机械工程学院教授、博士。主要研究方向为磨削加工与特种加工。E-mail:yanwang909909@163.com。王 帅，男，1988年生。上海理工大学机械工程学院硕士研究生。刘建国，男，1962年生。上海理工大学机械工程学院高级工程师。李德蔺，男，1993年生。上海理工大学机械工程学院硕士研究生。