2A12航空铝合金多轴疲劳试验及应力准则寿命预测模型研究

陈亚军 刘 波 刘辰辰 周 剑

1.中国民航大学中欧航空工程师学院，天津，3003002.中国南方航空股份有限公司，广州，510410

2A12航空铝合金多轴疲劳试验及应力准则寿命预测模型研究

陈亚军1刘 波2刘辰辰1周 剑1

1.中国民航大学中欧航空工程师学院，天津，3003002.中国南方航空股份有限公司，广州，510410

针对多轴疲劳失效问题，选取2A12航空铝合金进行应力幅比变量、相位差变量和平均应力变量的多轴疲劳试验。对常用的3种多轴疲劳应力准则寿命预测模型(即Lee准则、Carpinteri准则和Sines准则)进行讨论，并通过引入应力幅比参量和相位差参量，提出基于Carpinteri准则的修正模型。将不同条件下2A12航空铝合金的试验寿命与不同应力准则下模型的预测寿命进行比较，结果表明：Lee准则对上述多轴疲劳试验的预测结果过于危险；Carpinteri准则和Sines准则由于未考虑拉-扭应力幅比和相位差因素，预测寿命与实际寿命相比均出现了较大偏差；修正后的应力准则寿命预测模型在不同条件下90%的寿命预测数据在两倍误差带内。

2A12铝合金；多轴疲劳；应力准则；寿命预测；模型修正

0 引言

2A12航空铝合金是一种在民航领域应用广泛的硬铝合金，常被用于飞机结构件，如蒙皮、框肋、翼梁等工程结构件。这些结构件在复杂载荷环境下工作，常常受到多轴载荷作用而导致疲劳损坏。研究材料在不同加载方式下的疲劳特性并准确地预测多轴疲劳寿命，可以预防工程实践中的疲劳事故，更加合理地设计和运用材料。

近年来,多轴疲劳寿命预测模型的研究取得了一些进展，但是理论尚未完善。从种类上可以将现有的模型分为应力准则、应变准则、能量法以及临界平面法4类。其中,对于应力准则，GOUGH[1]给出的椭圆方程应力准则成为之后研究的基础。McDIAMID[2]提出了考虑裂纹扩展形式的准则，而CROSSLAND[3]通过引入静水应力参量，提出了针对非比例加载的应力准则。但是目前各种条件下的准则尚未统一[4-7]。对于应变准则和能量法的讨论较多，吴志荣等[8]结合临界平面思想，以最大切应变幅作为参量,提出一种对多种材料都具有较高预测精度的模型。孙楠楠等[9]则提出了一种基于总应变能的多轴疲劳模型，该模型适用于多种载荷形式。但是这些模型的验证都是基于应变控制的试验结果而进行的，基于应力控制的试验验证较少。时新红等[10]利用应力幅比变量试验对等效应力准则和应力不变量准则进行了验证，认为二者预测效果不好。本文采用应力控制方法进行多轴疲劳试验，进行3种变量的多轴疲劳试验，并比较分析常见应力准则的适用性。通过引入应力幅比和相位差因素，提出了一种新的修正模型，并进行了试验验证。

1 试验方法

1.1 试验材料及参数

采用民航领域使用广泛的硬铝合金2A12，室温下，其化学成分如表1所示，力学性能如表2所示。

表1 2A12铝合金化学成分(质量分数)Tab.1 Chemical constituent of aluminum alloy 2A12 (mass fraction) %

表2 2A12铝合金力学性能Tab.2 Mechanics properties of 2A12 aluminum alloy

试样尺寸如图1所示，参考GB/T3075—2008《金属材料疲劳试验轴向力控制方法》及GB/T12443—2007《金属材料扭应力疲劳试验方法》，设计了漏斗状的试样。

图1 铝合金疲劳试样Fig.1 Aluminum alloy fatigue test specimen

1.2 试验方案及结果

试验利用SDN100/1000 电液伺服拉扭复合疲劳试验机，采用拉压和扭转双通道应力控制，其中拉应力和切应力均为正弦波加载，表达式为

σ=σasinωt+σm

(1)

τ=τasin(ωt-φ)+τm

(2)

式中，σa为拉应力幅值；τa为切应力幅值；ω为角频率；t为加载时间；φ为拉压和扭转应力之间的相位差；σm为拉应力平均值，τm为扭转应力平均值。

拉应力和切应力的关系通过应力幅比λ=σa/τa表示。

轴向应力和扭转应力的计算公式分别为

(3)

(4)

式中，Fa为轴向应力幅值；Ma为扭转力矩；r为测量出的所用棒材的截面半径。

加载时的等效应力选用von Mises准则，其等效应力表达式为

(5)

本文进行的试验均保持等效应力σeq=350 MPa不变，设置加载频率为5 Hz。

1.2.1 应力幅比变量试验

应力幅比的不同会导致拉应力和扭应力的比例发生变化。在保持等效应力为350 MPa、拉扭相位差为0，并设置拉扭平均应力均为零的前提下，选取不同应力幅比进行多轴疲劳试验，试验参数以及结果见表3。

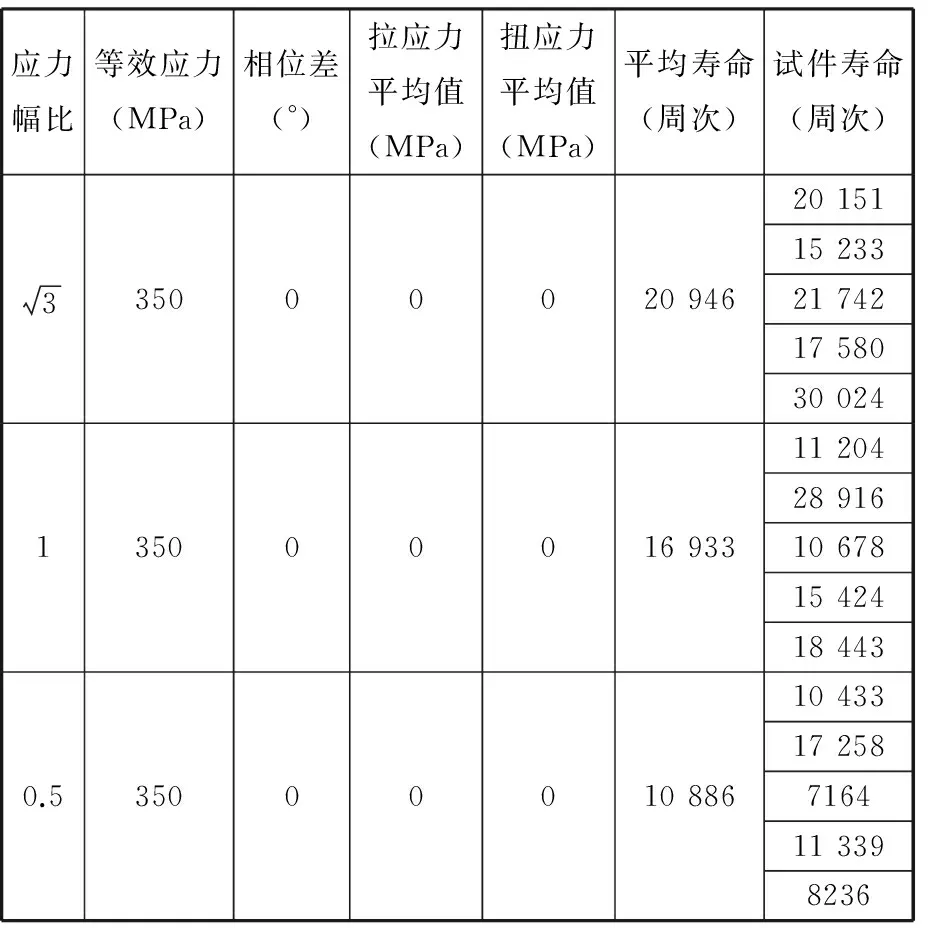
表3 应力幅比变量试验方案以及结果汇总Tab.3 Test procedure and results with stress-amplitude ratio variable

1.2.2 相位差变量试验

相位差的不同会导致载荷加载路径不同。试验保持等效应力、应力幅比和拉扭平均应力不变，选取4个相位差值，分别是0°，30°，60°和90°。不同相位差对应的载荷加载路径如图2所示。试验参数以及结果见表4。

1.2.3 平均应力变量试验

平均应力变量试验包括两部分，分别是拉应力平均值试验与扭应力平均值试验。试验保持拉扭应力幅值和相位差不变，分别使拉应力平均值和扭应力平均值变化，试验参数以及结果见表5。

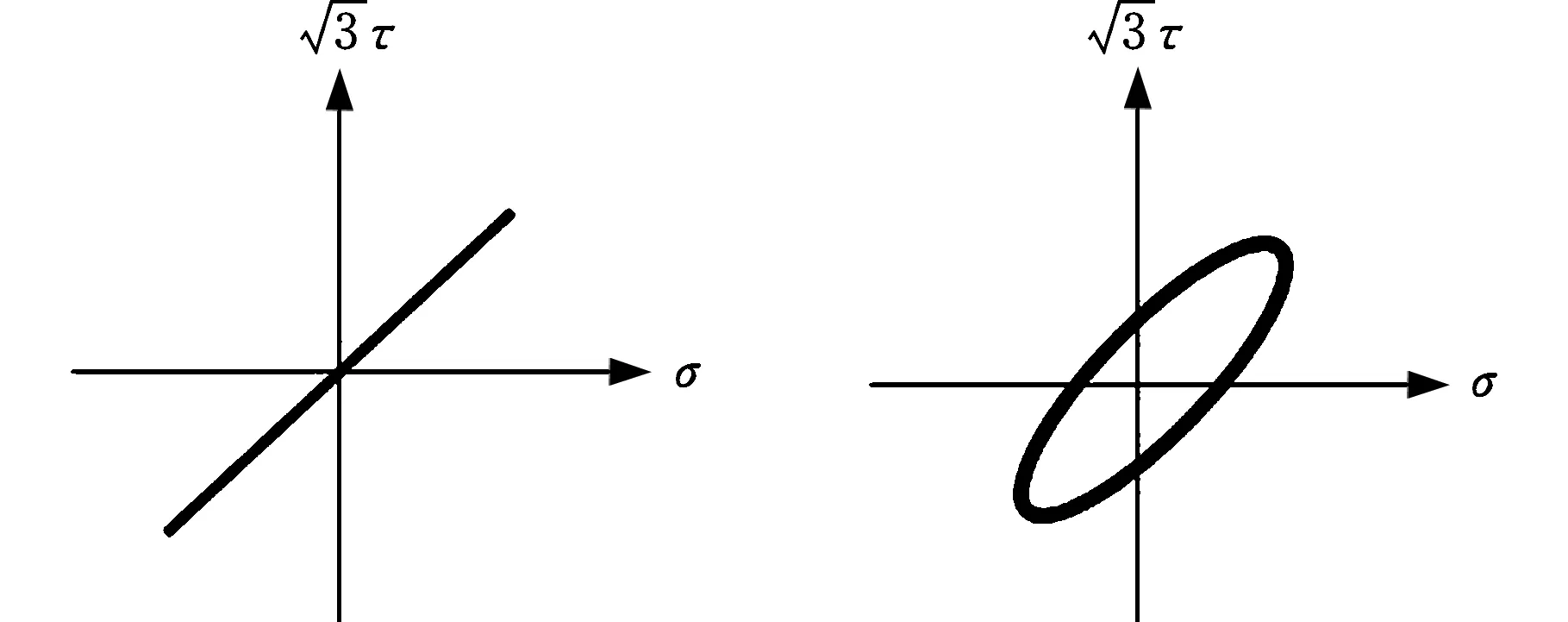
(a)0° (b)30°

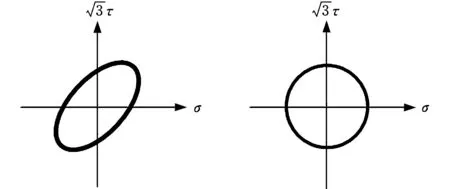
(c)60° (d)90°图2 不同相位差下的加载路径Fig.2 Loading route under different tension-torsion phase表4 相位差变量试验方案以及结果汇总Tab.4 Test procedure and results with tension-torsion phase variable

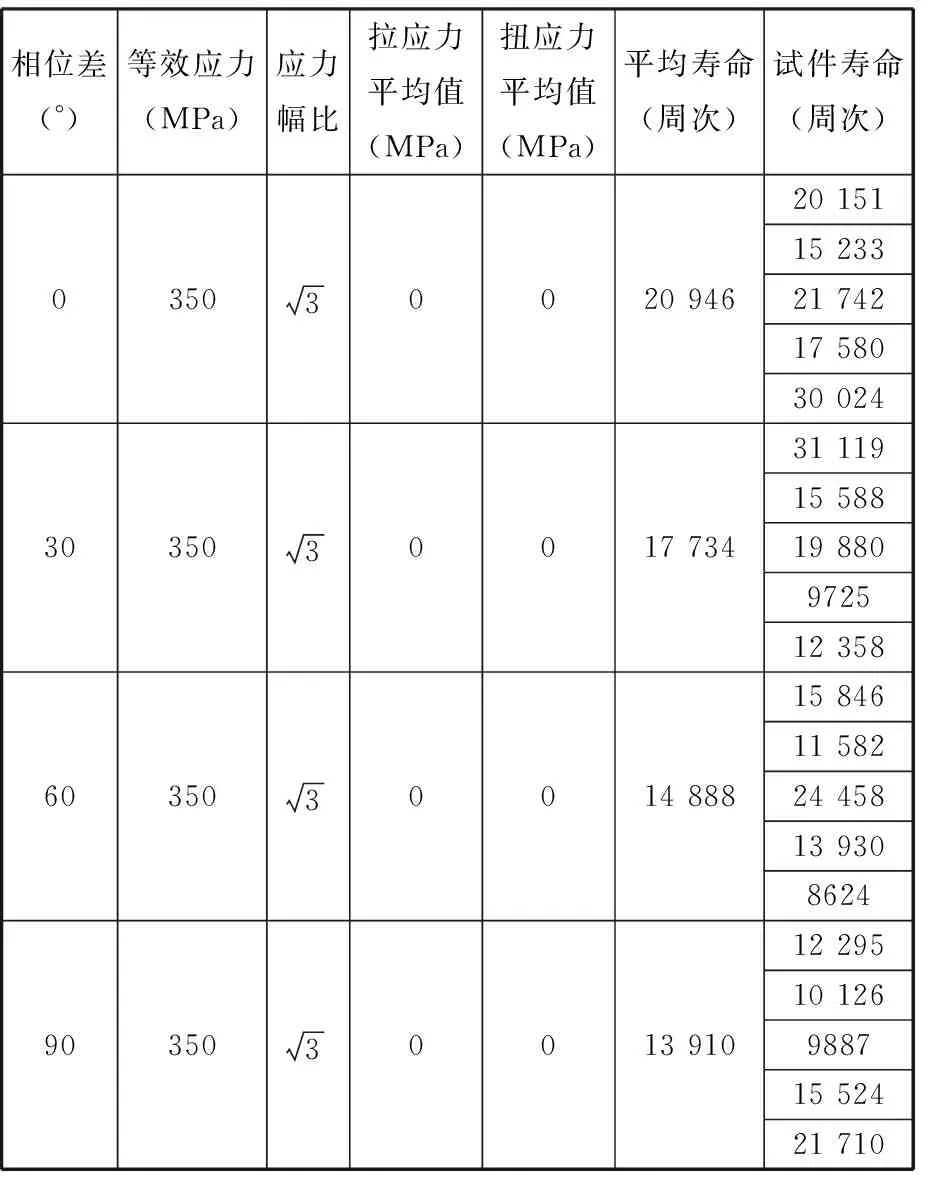
相位差(°)等效应力(MPa)应力幅比拉应力平均值(MPa)扭应力平均值(MPa)平均寿命(周次)试件寿命(周次)0350300209462015115233217421758030024303503001773431119155881988097251235860350300148881584611582244581393086249035030013910122951012698871552421710

2 应力准则及修正

考虑到本文的试验条件为应力控制，下面对3种常用的应力准则多轴疲劳寿命预测模型进行回顾，并对Carpinteri准则进行讨论和修正。

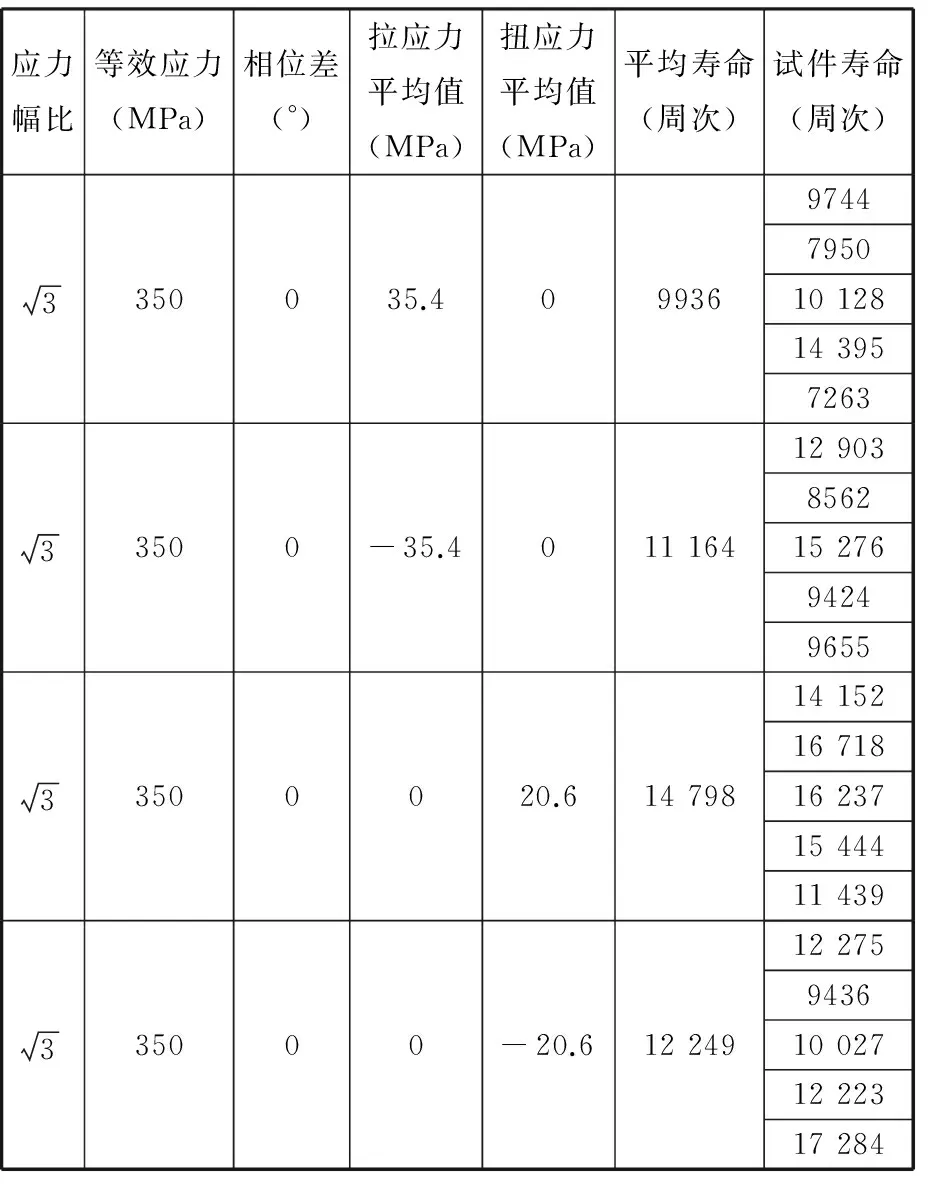
表5 平均应力变量试验方案以及结果汇总Tab.5 Test procedure and results with average stress variable

2.1 Lee准则

Lee准则[11]是一种等效应力准则，考虑了拉扭相位差因素的影响，其表达式为

(6)

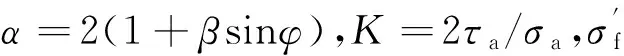
2.2 Carpinteri准则

Carpinteri准则[12]属于一种等效应力准则，其表达式为

(7)

式中,σmax为最大主应力。

2.3 Sines准则

Sines准则[13]是较为常用的一种应力不变量准则，其表达式为

(8)

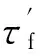
2.4 新模型的提出

Carpinteri准则考虑了最大主应力以及拉压、扭转疲劳极限等因素的影响，但是未考虑拉-扭应力幅比和相位差因素，故可以对其进行修正。

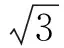
(9)

而考虑到相位差的周期性，对相位差取余弦值后发现，随着相位差余弦的增大，试验寿命呈上升趋势，如图3b所示。将(1+cos2φ)作为相位差参量代入模型，Carpinteri准则修正为

(10)

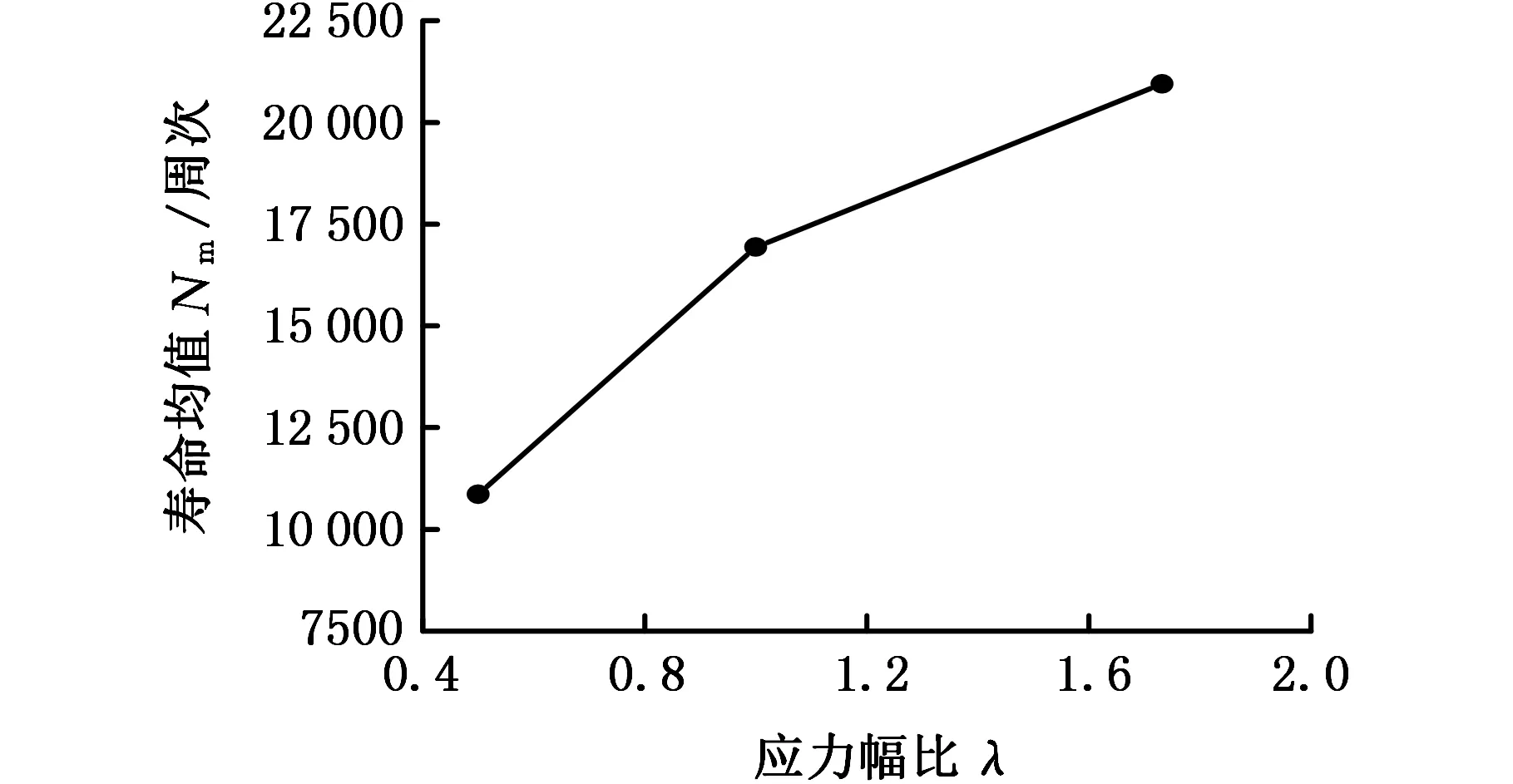
(a)应力幅比与疲劳寿命的关系

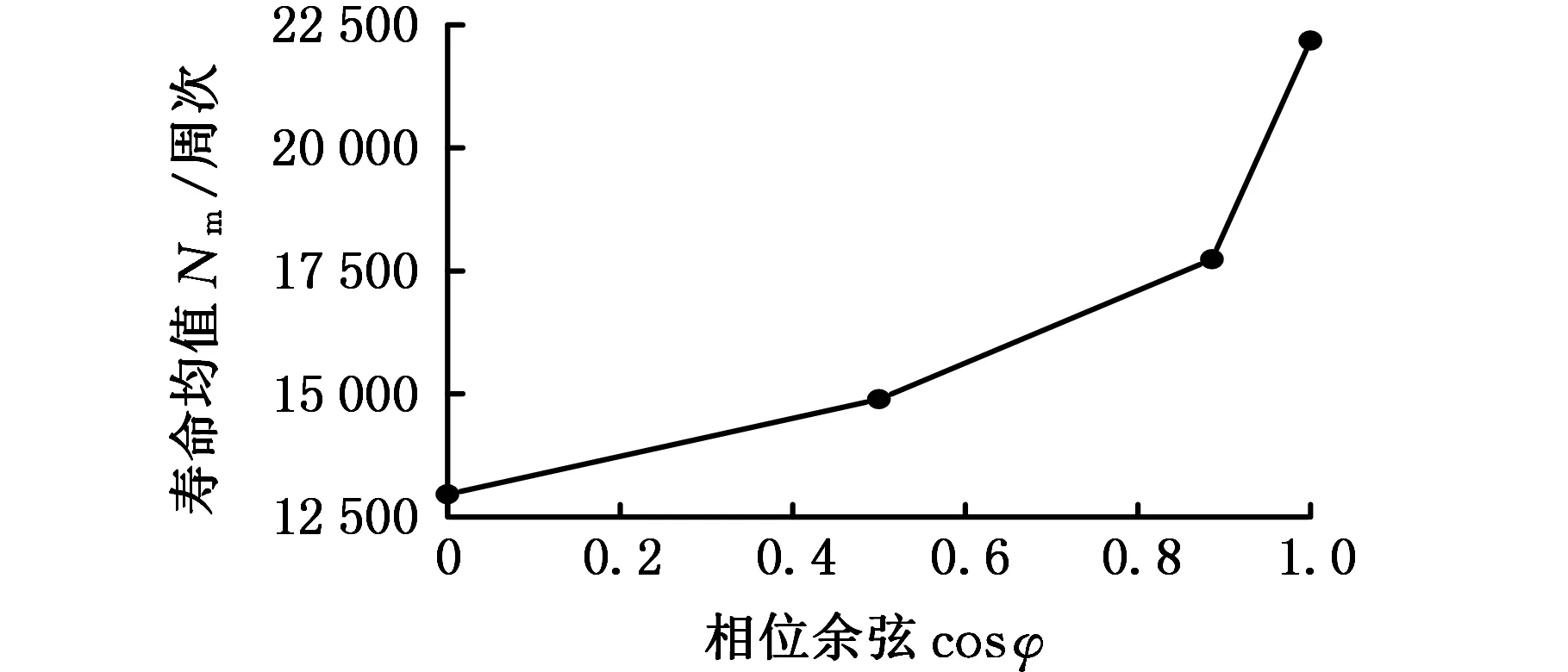
(b)相位余弦与疲劳寿命的关系图3 不同变量对疲劳寿命的影响Fig.3 Effects of different variables on fatigue life

3 寿命预测结果及分析

3.1 整体分析

图4所示为本文所做不同变量试验的疲劳寿命均值与各模型预测寿命之间的关系，可以发现，Lee准则的预测寿命与实际寿命相比偏差较大。Carpinteri准则预测结果较为保守，即预测寿命小于实际寿命，而Sines准则的部分预测结果不保守。本文提出的修正模型对于所有试验条件，预测寿命几乎全部分布于两倍误差带(虚线所围区域，下同)之内，预测效果相比于修正之前有了显著提升。

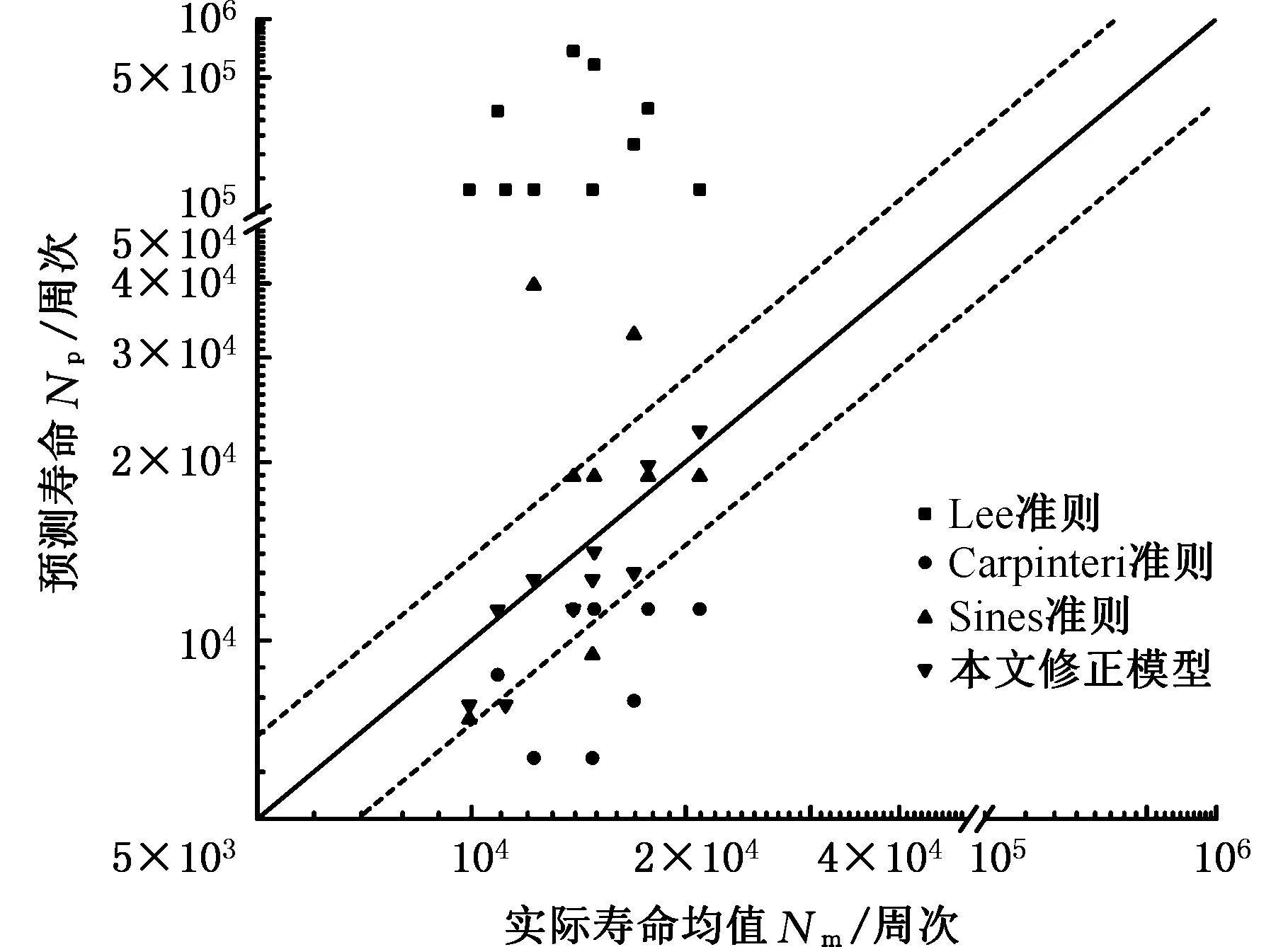
图4 试验寿命均值和预测寿命关系Fig.4 Relation between predicted life and average experimental life

3.2 应力幅比变量试验

图5所示为本文所做应力幅比变量试验的实际寿命与各模型预测寿命之间的关系。Lee准则的预测效果依旧不理想，与实际寿命偏差较大。Carpinteri准则的预测结果过于保守，而Sines准则的预测结果则较为危险。本文提出的修正模型引入了应力幅比参量，其预测结果好于其他3个准则，大部分预测结果分布于两倍误差带之内。

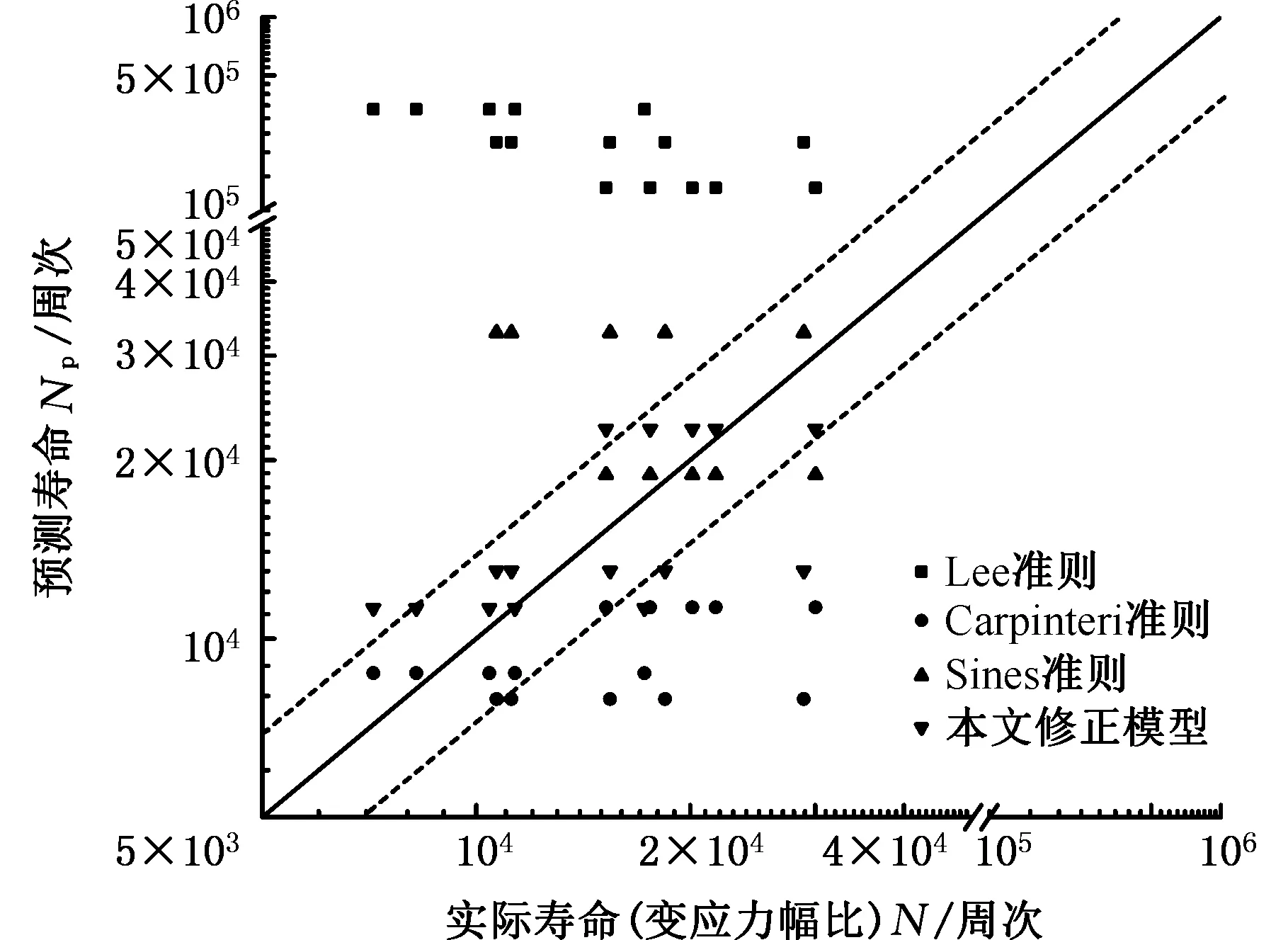
图5 应力幅比变量试验实际寿命和预测寿命关系Fig.5 Relation between predicted life and experimental life of stress-amplitude ratio variable experiments

3.3 相位差变量试验

对于相位差变量试验，其实际寿命和各模型预测寿命的关系如图6所示。虽然Lee准则考虑了相位差的影响，但是对于本文所做的相位差变量试验，预测效果较差。而Carpinteri准则和Sines准则，由于没有考虑相位差因素，故对于不同相位差加载试验，其预测结果相同，误差较大。而本文提出的修正模型，通过引入相位差参量，寿命预测值基本分布于两倍误差带之内。

图6 相位差变量试验实际寿命和预测寿命关系Fig.6 Relation between predicted life and experimental life of tension-torsion phase variable experiments

3.4 平均应力变量试验

对于平均应力变量试验，其实际寿命和各模型预测寿命关系如图7所示。Lee准则由于未考虑平均应力影响，不同条件下得到的预测寿命相等，且远大于实际寿命。Carpinteri准则对于平均应力变量试验的预测效果较差，预测寿命全部位于两倍误差带之外。Sines模型预测结果偏于危险。而本文提出的修正模型，预测寿命基本位于两倍误差带之内，取得了较好的预测效果。

图7 平均应力变量试验实际寿命和预测寿命关系Fig.7 Relation between predicted life and experimental life of average stress variable experiments

综合上述图表，将各个模型预测寿命在两倍误差带之内的个数占试样总数的百分比定义为预测准确率，统计结果如表6所示。

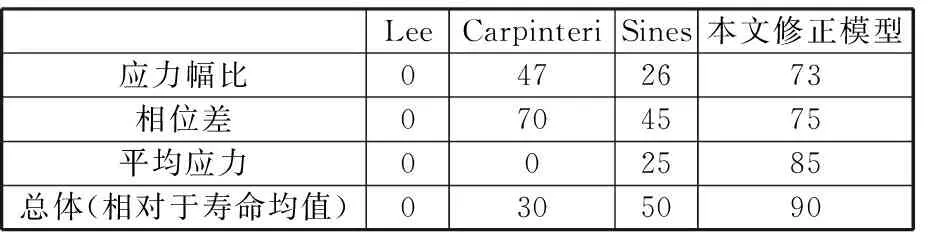
表6 各模型预测准确率Tab.6 Accuracy of prediction for different model %

4 结论

(1)对于本文所做试验设置的条件，Lee准则的预测寿命远大于实际寿命，结果过于危险。

(2)Carpinteri准则对于本文所设定的3种试验条件，预测结果均偏于保守，且认为相位差对多轴疲劳寿命没有影响，与试验结果不符。

(3)Sines准则的预测结果均出现了较大的偏差，对本文进行的多轴疲劳试验适用性不强。

(4)本文引入相位差和应力幅比参量，基于Carpinteri准则提出了优化模型，在不同试验条件下对多轴疲劳寿命的预测均取得了较好效果，预测结果中90%数据在两倍误差带之内。

[1] GOUGH H J. Crystalline Structure in Relation to Failure of Metals—Especially Fatigue[C]//Proc. ASTM, American Society for Testing and Materials. West Conshohocken, 1933，33:3-114.

[2] McDIARMID D L. A General Criterion for High Cycle Multiaxial Fatigue Failure [J]. Fatigue Fract. Engng. Mater. Struct., 1991, 14:429-453.

[3] CROSSLAND B. Effect of Large Hydrostatic Pressure on the Torsional Fatigue Strength of an Alloy Steel [C]//Proc.Int.Conf.on Fatigue of Metals. London:Institute of Mechanical Engineers, 1956:138-149.

[4] 程军圣, 袁毅, 喻镇涛,等. 考虑平均应力效应的Tovo-Benasciutti疲劳寿命预测模型[J]. 中国机械工程, 2015,26(2):196-199. CHENG Junsheng, YUAN Yi, YU Zhentao, et al. Predicative Methods of Tovo-benasciutti Fatigue Life under Considering Mean Stress Effects[J]. China Mechanical Engineering, 2015,26(2):196-199.

[5] 陈凌, 张贤明, 欧阳平. 一种基于连续损伤力学的低周疲劳寿命预测模型[J]. 中国机械工程, 2015, 26(18):2506-2517. CHEN Ling, ZHANG Xianming, OUYANG Ping. A Life Prediction Model for Low Cycle Fatigue Based on Continuum Damage Mechanic [J]. China Mechanical Engineering, 2015, 26(18):2506-2517.

[6] 申杰斌, 唐东林. 一种考虑应力梯度的疲劳寿命预测方法[J]. 中国机械工程, 2017, 28(1):40-44. SHEN Jiebin, TANG Dongli. Predicting Method for Fatigue Life with Stress Gradient [J]. China Mechanical Engineering, 2017, 28(1):40-44.

[7] 陈凌, 张贤明, 刘飞, 等. 镁合金低周疲劳寿命预测模型探讨[J]. 中国机械工程, 2017, 28(5):512-518. CHEN Ling, ZHANG Xianming, LIU Fei, et al. Discussion of Low Cycle Fatigue Life Prediction Models for Magnesium Alloys [J]. China Mechanical Engineering, 2017, 28(5):512-518.

[8] 吴志荣, 胡绪腾, 宋迎东. 基于最大切应变幅和修正SWT参数的多轴疲劳寿命预测模型[J]. 机械工程学报, 2013, 49(2):59-66. WU Zhirong, HU Xuteng, SONG Yingdong. Multi-axial Fatigue Life Prediction Model Based on Maximum Shear Strain Amplitude and Modified SWT Parameter [J]. Journal of Mechanical Engineering, 2013, 49(2):59-66.

[9] 孙楠楠, 李国祥, 白书战, 等. 基于总应变能的多轴疲劳模型研究[J]. 船舶力学, 2015, 19(4):406-411. SUN Nannan, LI Guoxiang, BAI Shuzhan, et al. Study on Multiaxial Fatigue Criterion Based on Total Strain Energy [J]. Journal of Ship Mechanics, 2015, 19(4):406-411.

[10] 时新红, 张建宇, 鲍蕊, 等. 比例加载下应力幅比对2A12-T4疲劳寿命的影响[J]. 北京航空航天大学学报, 2010, 36(8):965-968. SHI Xinhong, ZHANG Jianyu, BAO Rui, et al. Effect of Stress Amplitude on High-cycle Fatigue Life of 2A12-T4 Aluminum Alloy under Proportional Loading [J]. Journal of Beijing University of Aeronautics and Astronautics, 2010, 36(8):965-968.

[11] LEE S B. A Criterion for Fully Reversed Out-of-phase Tors Ion and Bending[C]//. Multiaxial Fatigue. San Francisco:ASTM STP, 1985:553-568.

[12] CARPINTERI A, SPAGNOLI A. Multiaxial High-cycle Fatigue Criterion for hard Metals [J]. International Journal of Fatigue,2001,23(2):135-145.

[13] SINES G, OHGI G. Fatigue Criterion under Combined Stresses or Strains [J]. Journal of Engineering Materials Technology, 1981, 103(2):82-90.

(编辑 苏卫国)

Multiaxial Fatigue Test of Aeronautical Aluminum Alloy 2A12 and Research on Stress Criterion Life Predictive Model

CHEN Yajun1LIU Bo2LIU Chenchen1ZHOU Jian1

1.Sino-European Institute of Aviation Engineering,Civil Aviation University of China,Tianjin,300300 2.China Southern Airlines Company Limited,Guangzhou，510410

Based on multiaxial fatigue failures, compound fatigue tests of stress-amplitude ratio, tension-torsion phase and average stress variables were carried out on 2A12 aluminum alloy. With the discussions of 3 common multiaxial fatigue life predictive models of stress criterion which included Lee criterion, Carpinteri criterion and Sines criterion, a modified model was built on the basis of Carpinteri criterion considering effects of both stress-amplitude ratio and tension-torsion phase. The comparison between predicted life and experimental life under different conditions shows that Lee criterion’s predictive results are too over-estimated for the above experiments. Without consideration of stress-amplitude ratio and tension-torsion phase, the predicted life of Carpinteri criterion and Sines criterion have large errors compared with the experimental life. The new modified stress criterion life predictive model may give results that 90 percent of life prediction data will be in the 2 times error band with different conditions.

2A12 aluminum alloy； multiaxial fatigue； stress criterion； life prediction； model modification

2016-08-15

国家自然科学基金资助项目(11502285)；中央高校基本科研业务费专项资金资助项目(3122016U003)

O346.2

10.3969/j.issn.1004-132X.2017.09.015

陈亚军，男，1976年生。中国民航大学中欧航空工程师学院副教授、博士。主要研究方向为飞机结构材料疲劳失效等。E-mail:2292598008@qq.com。刘 波，男，1989年生。中国南方航空股份有限公司助理工程师。刘辰辰，男，1994年生。中国民航大学中欧航空工程师学院硕士研究生。周 剑，男，1990年生。中国民航大学中欧航空工程师学院硕士研究生。