李晓璐:“观察物体(二)”教学设计
2017-05-16李晓璐
李晓璐

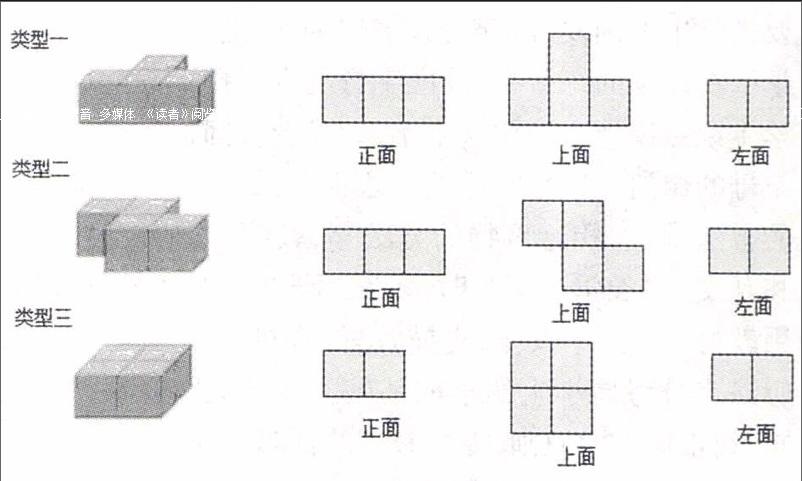
教学内容:人教版义务教育教科书小学《数学》四年级下册。
教学目标:
1.使学生能正确辨认从不同方向观察用几个正方体搭成的几何体的形状。
2.让学生经历观察的过程,认识到从不同的位置观察物体,看到的形状可能不同。
3.通过操作、观察、想象、判断等活动,培养学生的空间想象和推理能力。
教学重点 :通过观察,正确辨认从不同方向观察到的物体的形状。
教学难点 :在实际观察活动中,从观察到的物体抽象出平面圖形。
教学准备:课件、立方体模型、方格纸。
教学方法:整节课主要采用观察、发现、验证等教学方法,强调多种教学方法的交叉使用和互相配合,重点采用多媒体教学手段。
教学过程:
一、激情引趣,引入新课
师:同学们,在上课前咱们一起来玩一个猜谜游戏,猜猜图中有几个人,分别都是咱班的谁?(提前找班级三个身高、体重相差不多的同学拍三组照片,投影出示左侧图。)
生1:一个人、两个人、三个人……
生2:张明、王红……
师:看来同学们有很多异议,我们再来看下面的照片。(投影出示上面图。)
生1:三个人。
生2:李丽、赵磊……
师:通过这张图片我们确定是三个人了,可是具体是谁还有异议,那下面我们接着看。(投影出示前面图。)
生:张明、赵磊、王红。
师:我们都猜出了照片里的同学,刚才的三张照片照的都是同样的同学,有什么区别呢?
生:一张是从左面照的,一张是从上面照的,一张是从正面照的。
师:在生活中我们要从多角度观察物体,通常我们从哪几个方向观察物体?
生:从正面看、从上面看和从左面看。(教师板书:观察物体从前面看、从上面看、从左面看。)
【设计意图:从生活的实际现象引入新课,根据学生已有的数学经验和生活经验明确研究主题。充分调动学生的积极性,激发学生研究兴趣的同时,为学生的学习指明方向。】
二、合作探究,学习新知
1.从不同方向观察同一物体。
师:这里有四个小正方体组成的立体图形,三位同学分别从不同方向进行了观察。我们一起猜猜他们都是从哪几个方向进行观察的。
生:小华从左面看的,小强从正面看的,小红从上面看的。
师:你们同意吗?在你们的桌子上也有四个小正方体,你也来试试搭出这样的图形观察一下吧。( 生活动,师巡视指导。)谁愿意来展示一下你的作品和观察结果?(生展示作品。)
师:谁的观察结果和他的一样? (生举手。)
师:这么多同学都和他一样,刚才我们分别从正面、上面、左面观察了同一个立体图形,可观察到的这些图形都是一样的吗?
生:不一样。
师:也就是说从不同方向观察一个立体图形,所看到的形状是——
生:不同的。
【设计意图:通过让学生亲自动手操作实践,让学生切身感受到对于同一物体从不同方向观察形状是不同的,观察与想象是培养学生良好思维品质不可缺少的要素。为下面的学习奠定基础的同时,培养了空间观念,提升了学生的观察能力。】
2.开放思维,观察不同立体图形。
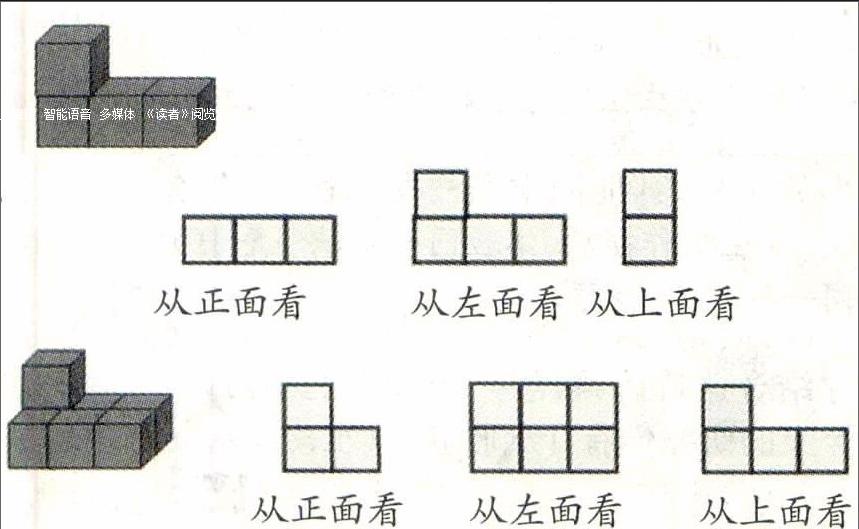
师:刚才我们一起观察了这个由老师搭成的立体图形,你们想不想自己试试搭出其他的立体图形来观察一下呢?(教师巡视,找几个学生任意将四个小正方体拼摆成几何体。)
师:我们看一下这几位同学摆的立体图形,咱们试试在方格纸上画出这个几何体从正面、上面和左面看到的形状。(生动手操作。)
【设计意图:充分调动了学生主动、开放、积极的学习活动兴趣。让学生个性化活动,培养学生的空间想象力。】
3.小结方法。
师:我们已经观察了三个不同的几何体,结果和大家想象的相同吗?那你们在想象的过程中有什么方法吗?同桌讨论一下。
生1:先确定集合体的长、宽、高。
师:从正面、上面和左侧面分别看到的是几何体的什么?
生2:从正面看到的是几何体的长和高。
生3:从上面看到的是几何体的长和宽。
生4:从左面看到的是几何体的宽和高。
【设计意图:学生讨论探究,教师帮助学生总结提炼方法,培养学生探索知识本质的习惯和意识,有助于学生对知识的理解和对概念的总结。】
三、巩固提高
1.基础练习。
下面的图形分别是小强从什么位置看到的?连一连。
从正面看 从左面看 从上面看
2.提高练习。
从正面看 从左面看 从上面看
【设计意图:通过连一连、找一找、想一想和猜一猜的活动,使学生认知得到巩固,为后续课程的学习打下基础。在巩固所学知识的基础上,拓展学生视野,掌握观察物体的方法。】
四、提炼升华
师:同学们,通过今天的研究你有什么收获吗?
生:要全面观察。
师:是的,观察要全面。请看屏幕,看到这张图片你有什么感受?
师:如果我们换个角度再来看看,你又有什么发现?
师小结:有时候换个角度看,你会发现,人生原有另一番滋味,另一道风景。正如苏轼的《题西林壁》:“横看成岭侧成峰,远近高低各不同。不识庐山真面目,只缘身在此山中。”
【设计意图:通过跨学科的知识联系,让学生感受到数学就在自己的身边,产生对数学的亲切感。让学生在比较中发现美、感知美、欣赏美、追求美。】
