关键节点与非关键节点物流企业合作

2017-05-12徐耀群程林

商业研究 2017年4期

徐耀群+程林

内容提要：针对物流企业进行合作的外部正效应问题，本文通过建立关键节点与非关键节点物流企业合作演化博弈模型进行分析求解，结果表明关键节点与非关键节点物流企业的合作策略与双方合作收益密切相关，当双方合作收益不断变化时就会出现多种演化稳定均衡；如果“搭便车”行为从对方采取合作策略中获得的收益很大，则物流企业进行合作的积极性会降低。因此，物流行业协会应进行调控，对“搭便车”行为进行惩罚，促使物流企业进行合作；对于合作收益增长比较小的物流企业给予奖励，以激励他们进行合作，提高物流企业整体的信誉。

关键词：物流企业；合作；演化博弈；关键节点

中图分类号：F203文献标识码：A文章编号：1001-148X（2017）04-0129-06

随着经济社会的发展，网购的兴起，物流在国民经济中扮演的角色越来越重要，为推动国民经济的发展起到了积极的作用。调查显示，我国物流行业的产值占国内生产总值的10%以上。物流行业不仅数量众多，企业的规模也大小各异。这些物流企业之间资金、信息和人员的相互流动，构成了一个复杂的关系网络。在这个网络当中，每一个物流企业可以看做其中的一个节点。那些重要程度高，对相邻节点影响大且相邻节点数量多的节点企业为关键节点物流企业，一般规模大、资金雄厚、人员多、地理位置优越。而非关键节点物流企业多是那些规模较小、地理位置偏僻、影响力小的公司。物流企业之间加强合作对于节约成本、提高效率、增强效益具有积极的意义。关键或非关键物流企业之间加强合作具有外部正效应，二者对于增强消费者信赖程度，提高物流行业整体的信誉，扩大市场份额具有积极的意义。

演化博弈论将动态演化过程和博弈理论相结合，是20世纪70年代随着Maynard和Price以及Maynard提出演化稳定策略（ESS）概念而产生的。演化博弈个体之间通过模仿、学习等过程实现动态平衡，被广泛应用到经济管理领域。由于无论是关键节点物流企业还是非关键节点物流企业往往具有有限理性，很难在一次决策中作出最优选择，因而运用演化博弈分析关键节点物流企业之间与非关键节点物流企业之间合作的策略均衡，更能代表现实中博弈方的策略选择，从而使分析结果更具现实意义。本文拟在演化博弈的基础上研究关键节点物流企业之间和非关键节点物流企业之间的合作问题，通过考察建立合作关系收益水平的变化，分析双方的行为策略，运用复制动态机制求解出关键节点物流企业之间和非关键节点物流企业之间合作的演化稳定策略。

一、基本假设与模型建立

假设存在关键节点物流企业和非关键节点物流企业两个群体，从关键节点物流企业群体中随机选取一家与非关键节点物流企业进行配对并博弈。关键节点物流企业和非关键节点物流企业都是有限理性的，他们通过学习不断改变自身策略直到达到一个均衡为止。在原物流行业体系的基础上，关键节点物流企业和非关键节点物流企业的行为策略空间为（进行合作，不进行合作），简记（T，F）。假设如下：

（1）若关键节点物流企业和非关键节点物流企业都不进行合作，则此时他们的正常收益分别是Pm，Pr，Pm>0，Pr>0。

（2）若关键节点物流企业和非关键节点物流企业都进行合作，则物流行业的整体市场需求量会增加，此时他们的收益分别为Pm+α-Cm，Pr+β-Cr，其中α（α>0）为关键节点物流企业进行合作增加的收益。β（β>0）为非关键节点物流企业进行合作增加的收益。Cm为关键节点物流企业为进行合作投入成本，Cr为非关键节点物流企业为进行合作投入成本，Cm>0，Cr>0。

（3）当只有关键节点物流企业进行合作时，则他占据的市场份额会增加，此时关键节点物流企业的收益为Pm+α-Cm，而非关键节点物流企业则由于自己的“搭便车”行为获得了比原来不进行合作更多的收益。因此，若关键节点物流企业进行合作，非关键节点物流企业不进行合作，则前者的收益为Pm+α-Cm，后者的收益为Tr（Tr>Pr）。

（4）当只有非关键节点物流企业进行合作时，此时这些企业的收益为，而关键节点物流企业由于“搭便车”行为而获得的收益为Tm（Tm>Pm）。

根据上面的假设，建立博弈的策略矩阵和博弈的支付矩阵（A表示关键节点物流企业，B表示非关键节点物流企业），分别如表1和表2所示。

二、关键节点和非关键节点物流企业合作的演化博弈分析

（一）演化过程的平衡点

假设在关键节点物流企业群体A中，选择合作策略的比例为x（0x1），非关键节点物流企业群体B中，选择合作策略的比例为y（0y1），则关键节点物流企业和非关键节点物流企业群体中选择不合作策略的比例分别为（1-x）和（1-y）。

对于关键节点物流企业来说，选择合作策略的适应度为：

选择不合作策略的适应度为：

平均适应度为：

根据Malthusian方程，A选择合作策略的数量的增长率等于其适应度U1T减去平均适应度U1〖TX-〗，t为时间，整理得复制动态方程：

命题1：该系统的平衡点为（0，0）、（0，1）、（1，0）、（1，1）。当α1<α<α2，β1<β<β2时，（xT，yT）也是系统的平衡点。

证明：对于系统（I），分别令，显然有（0，0）、（0，1）、（1，0）、（1，1）是系统的平衡点。当α1<α<α2，β1<β<β2时，0

（二）平衡点的稳定性分析

复制动态方程求出的平衡点不一定是系统的演化稳定策略（ESS），根据Friedman提出的方法，演化平衡点的稳定性可以从该系统的雅可比（Jacobian）矩阵（记为J）的局部稳定分析导出。

其中：

如果下列条件得到满足：（1）（迹条件，其值記为trJ）（雅可比行列式条件，其值记为detJ）。复制动态方程的平衡点就是（渐近）局稳定的，该平衡点就是演化稳定策略（ESS）。系统的平衡点分析见表3。

命题2：（1）若0<α<α1，0<β<β1，系统（I）演化稳定策略（ESS）为（F，F），平衡点的局部稳定性分析见表4；（2）若0<α<α1，β1<β<β2，系统（I）演化稳定策略（ESS）为（F，T），平衡点的局部稳定性分析见表5；（3）若α1<α<α2，0<β<β1，系统（I）演化稳定策略（ESS）为（T，F），平衡点的局部稳定性分析见表6；（4）若α1<α<α2，β1<β<β2，系统（I）演化稳定策略（ESS）为（F，T）和（T，F），平衡点的局部稳定性分析见表7；（5）若α>α2，β>β2，系统（I）演化稳定策略（ESS）为（T，T），平衡点的局部稳定性分析见表8。

证明：根据上述判断方法，可计算出雅可比矩阵J在各个平衡点的迹的值和行列式，并判断其局部稳定性。因此，各种情况下的演化稳定分析结果分别如上所述，证毕。

（三）演化结果分析

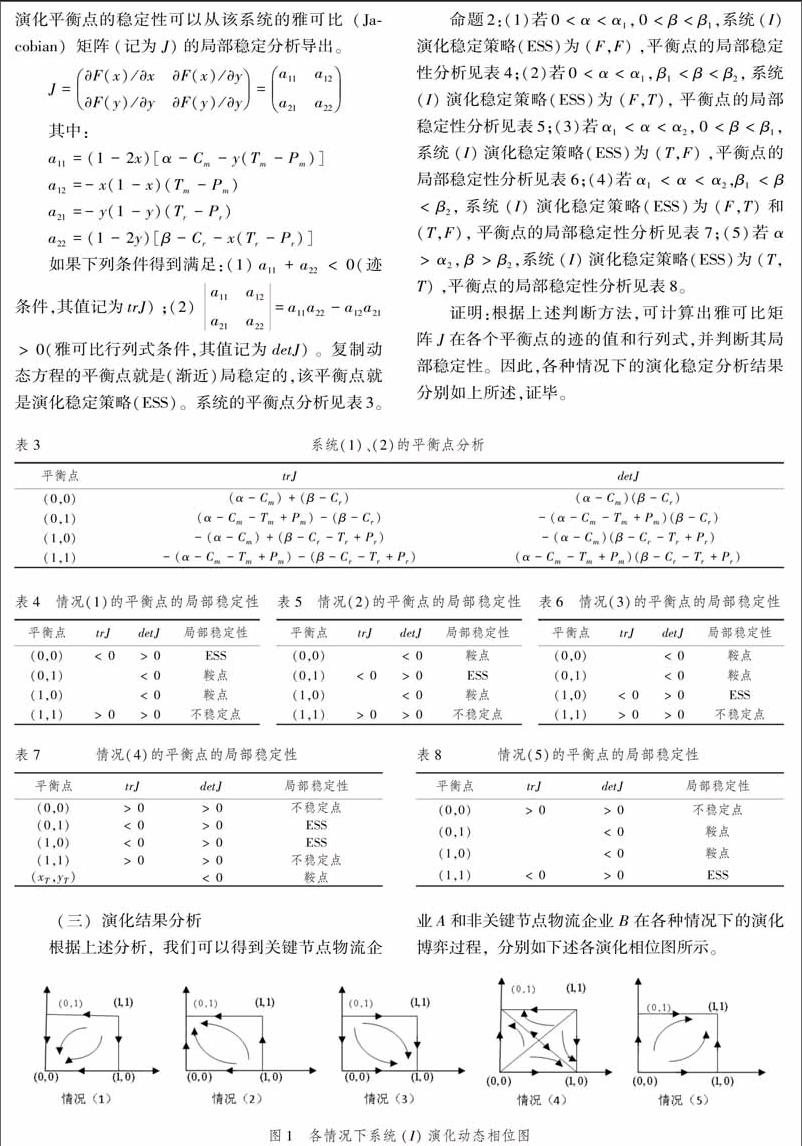
根据上述分析，我们可以得到关键节点物流企业A和非关键节点物流企业B在各种情况下的演化博弈过程，分别如下述各演化相位图所示。

由以上系统动态演化相位图，我们可以得到如下的分析结果：

（1）当关键节点物流企业和非关键节点物流企业双方进行合作的收益增加值α、β都比较小，0<α<α1，0<β<β1，双方却为此付出了投入成本，如图1情况（1）所示，此时（0，0）是演化稳定点，（0，1）和（1，0）是鞍点，（1，1）是不稳定点，关键节点物流企业和非关键节点物流企业都不进行广告投入是演化稳定策略。

（2）当非关键节点物流企业进行合作增加的收益β增大到一定程度β1<β<β2，此时他进行合作增加的收益大于付出的成本，但却小于此时他采取“搭便车”行为获得的收益Tr。此时非关键节点物流企业进行合作增加的收益α不变，但其付出的成本远大于进行合作增加的收益，关键节点物流企业不进行合作，非关键节点物流企业的“搭便车”行为无法实施，如图1情况（2）所示，此时（0，1）是演化稳定点，（0，0）和（1，0）是鞍点，（1，1）是不稳定点，即关键节点物流企业不进行合作，而非关键节点物流企业进行合作是演化稳定策略。

（3）当关键节点物流企业进行合作的收益增加值α增大到一定程度α1<α<α2，其进行合作增加的收益大于付出的成本，但却小于此时采取“搭便车”行为获得的收益Tm。此时非关键节点物流企业进行合作增加的收益β不变，因此他不会进行合作，关键节点物流企业的“搭便车”的行为无法实现，如图1情况（3）所示，（1，0）是演化稳定点，（0，0）和（0，1）是鞍点，（1，1）是不稳定点，即非关键节点物流企业不进行合作，而关键节点物流企业进行合作是演化稳定策略。

（4）当关键节点物流企业与非关键节点物流企业双方的收益增加值分别为α1<α<α2，β1<β<β2，双方进行合作增加的收益大于他们为此付出的成本，却分别小于采取“搭便车”行为所获得的收益Tm、Tr，如图1情况（4）所示，（0，1）和（1，0）是演化稳定点，（xT，yT）是鞍点，（0，0）和（1，1）是不稳定点。此时，关键节点物流企业进行合作，非关键节点物流企业不进行合作或关键节点物流企业不进行合作，非关键节点物流企业进行合作是演化稳定策略，但具体会沿着哪一条路径到哪一种状态与博弈的支付矩阵和系统的初始状态都有关。

（5）当关键节点物流企业和非关键节点物流企业进行合作增加的收益都比较大，且分别为α>α2，β>β2，双方进行合作所增加的收益不仅大于他们为此而付出的成本，还大于此时采取“搭便车”行为所获得的收益Tm、Tr。如图1情况（5）所示，（1，1）是演化稳定点，（0，1）和（1，0）是鞍点，（0，0）是不稳定点。此时，关键节点物流企业和非关键节点物流企业都进行合作是演化稳定策略。

三、物流行业调控下的演化分析

由上述分析可知，如果物流企业进行合作所增加的收益小于为此其投入的成本，或者企业采取“搭便车”行为带来的收益大于企业进行合作所增加的收益，那么物流企业不会选择进行合作。为了促进物流行业健康发展，树立物流企业整体的信誉，物流行业协会需要进行调控，促成物流企业之间的合作。物流行业协会的调控措施可以概括为惩罚机制和奖励机制。

（一）惩罚机制下的演化分析

根据上述分析可知当和

，物流企业会采取“搭便车”行为，不进行合作，因此物流行业协会会对其实施一定的罚款。假设物流行业协会的罚款金额为A，此时物流企业进行合作的收益矩阵如表9所示。

此时的Malthusian方程为：

命题3：系统（3）、（4）的平衡点为（0，0）、（0，1）、（1，0）、（1，1），（xT1，yT1）也为系统的平衡点，当且仅当下面的不等式成立：

。系统的平衡点分析见表10。

命题4：（1，1）是上述系统唯一的ESS的充要条件是：

证明：从表9对平衡点的分析可知，（1，1）是系统唯一的ESS的充要条件为detJ>0，trJ<0，即：，且：

，因此：

由表9可知，（0，0）是系统的不稳定点，（0，1）和（1，0）是系统的鞍点，（1，1）是唯一的ESS，证毕。

当时，关键节点物流企业和非关键节点物流企业都没有进行合作的动机，但只要物流行业协会的惩罚力度A比物流企业采取“搭便车”行为获得的收益与进行合作所获得的收益之差大时，物流企业会倾向于进行合作。因此，行业监管协会采取有力的措施惩罚投机者，减少“搭便车”行为的发生，从而增加物流企业进行合作的可能性，提高物流行业整体的信誉。

（二）奖励机制下的演化分析

如果物流企业进行合作增加的收益比较小时，即0<α<α1，0<β<β1，物流行业协会可以通过奖励机制的方式引导其进行合作。此時，若关键节点物流企业或非关键节点物流企业采取策略T，物流行业协会会给予一定的奖励。假设行业协会的奖励值为B，此时物流企业进行合作的收益矩阵如表11所示。

此时的Malthusian方程为：

也为系统的平衡点，当且仅当下面的不等式成立：

命题6：（1，1）是系统唯一的ESS的充要条件是：

证明：同命题4。

命题6表明，当物流企业进行合作所增加的收益比较小时，即0<α<α1，0<β<β1，当行业协会对物流企业选择合作进行奖励，且奖励的金额要足够大，使得物流企业选择“搭便车”获得的收益小于进行合作获得的收益，这样奖励措施才起到作用，物流企业才会倾向于选择合作。

四、结论

本文通过对物流企业合作的演化博弈分析，研究了关键节点物流企业和非关键节点物流企业的行为策略。研究结果表明，关键节点物流企业与非关键节点物流企业行为策略的选择不仅与他们合作收益密切相关，还和双方“搭便车”行为所获得的收益相关。当物流企业合作收益增长不断变化时，会依次出现（不合作，不合作）、（合作，不合作）、（不合作、合作）和（合作、合作）等共存的演化稳定策略。如果“搭便车”行为从对方进行合作中获得的收益比较大，则关键节点物流企业和非关键节点物流企业进行合作的积极性会大大降低。物流行业协会为了促进物流企业整体的健康发展，应当采取一定的措施促使物流企业进行合作：对于采取“搭便车”行为的物流企业，行业协会要实行惩罚措施，并且只有当惩罚力度足够大时，这种惩罚措施才有作用；对于进行合作所增加的收益比较小的物流企业，行业协会要采取奖励措施激励其进行合作，并且只有当奖励值足够大时，这种奖励机制才有效。

参考文献：

[1]Maynard S J， Price G R.The logic of animal conflict [J].Nature， 1973， 246（2）：15-18.

[2]Maynard S J.The theory of games and theevolution of animal conflict [J].Journal of Theoretical Biology， 1974，47（1）：209-221.

[3]Webull J.Evolutionary game theory[M].Boston： Priceton Press， 1998：32-48.

[4]Xiao Tiaojun， Chen guohua.Wholesale pricing and evolutionary stable strategies of retailers with imperfectly observable objective[J].European Journal of Operational Research， 2009，196（3）：1190-1201.

[5]Zhu Qinghua， Dou Yijie.Evolutionary game model between governments and core enterprises in greening supply chains[J].System Engineering Theory and Practice， 2007，27（12）：85-89.

[6]黃敏枚.基于演化博弈的供应链协同产品开发合作机制研究[J].中国管理科学，2010，6（18）：155-162.

[7]周漩，张凤鸣，李克武，惠晓滨，吴虎胜.利用重要度评价矩阵确定复杂网络关键节点[J].物理学报，2012（5）：43-49.

[8]韩小花，薛声家.竞争的闭环供应链回收渠道的演化博弈决策[J].计算机集成制造系统，2010（7）：1487-1493.

[9]许民利，王俏，欧阳林寒.食品供应链中质量投入的演化博弈分析[J].中国管理科学，2012（10）：131-141.

[10]韩忠明，吴杨，谭旭升，段大高，杨伟杰.面向结构洞的复杂网络关键节点排序[J].物理学报，2015（5）：102-107.

[11]林挺，李杨，张亮.食用农产品供应链中节点间知识共享行为的演化博弈分析[J].科技管理研究，2015（18）：141-144.

[12]王鹏.食品供应链协同机制的演化博弈模型研究[J].科技创新与应用，2016（13）：47.

[13]苗瑞丽.基于复制动态的食品供应链演化博弈分析[J].现代商贸工业，2012（1）：272-273.

[14]慕静，马丽丽.基于SD的食品供应链信息共享演化博弈分析[J].科技管理研究，2015（3）：182-185.

[15]张俊，孙利波.核心制造企业与供应商演化博弈及价格管理系统开发[J].机械制造，2013（4）：1-3.

（责任编辑：周正）

收稿日期：2016-12-13