例谈构造函数，巧解（证）不等式

☉重庆市梁平中学 李继浪

例谈构造函数，巧解（证）不等式

☉重庆市梁平中学 李继浪

近几年，解（证）不等式是高考的热点之一，也是难点之一，学生常常感到束手无策，无从下手.如果灵活构造函数并利用函数的性质，往往能使问题迎刃而解.如何构造函数，构造什么样的函数，许多同学找不到突破口，感到无所适从.下面就此问题作出探讨.

一、构造一次函数，利用单调性解不等式

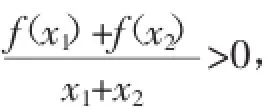
分析：由已知得出m2-2am+1≥1对任意a∈［-1，1］恒成立后，直接求参数m比较麻烦，如果反客为主，改变主元，即把a当作未知数，构造关于a的一次函数，问题较易解决.

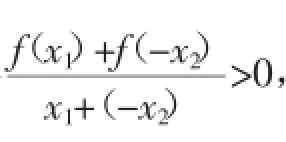
不等式f（x）≤m2-2am+1对所有x∈［-1，1］，a∈［-1，1］恒成立，即m2-2am+1≥1对任意a∈［-1，1］恒成立，即2ma-m2≤0对任意a∈［-1，1］恒成立.

故m的取值范围是（-∞，-2］∪｛0｝∪［2，+∞）.

二、构造二次函数，利用判别式证不等式

例2证明柯西不等式：设有非零实数组a1，a2，…，an及实数组b1，b2，…，bn，则（+a2n），当且仅当bi=λai（i=1，2，…n）时等号

分析：柯西不等式是高考中的选考内容.如何证明该不等式，方法很多，这里谈的是如何构造二次函数来证明.根据不等式的结构特点和二次函数判别式的特点构造二次函数，对学生有一定难度.

证明：构造二次函数f（x）=（a2n）x2+2（a1b1+ a2b2+…+anbn）x+（b2

1+a22+…+a2

n＞0且f（x）=（a1x+b1）2+（a2x+b2）2+…+（anx+bn）2≥0，所以Δ≤0，即4（a1b1+a2b2+…+anbn）2-4（a21+a2n）.因为a2

1+b22+…+b21+a22+…+a2

2

+…+a2n）（b21+b22+…+b2n）≤0，即（a1b1+a2b2+…+anbn）2≤（a21+

当且仅当aix+bi=0（i=1，2，…，n），即bi=-xai时，取等号，所以λ=-x.

三、构造指数函数，利用函数的单调性证不等式

分析：根据题目所给函数，其形式符合指数函数，所以考虑构造指数函数来处理

证明：先证充分性.

再证必要性，用反证法.

四、构造“形似”函数

分析：题目所给不等式具有分式形式，所以可先构造分式函数，再通过求导，利用函数的单调性来证明.

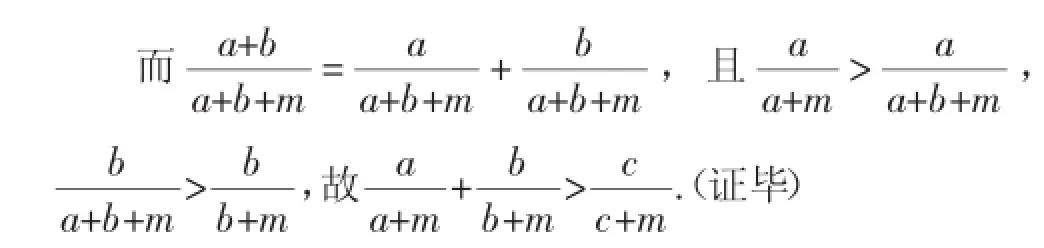
分析：题目所给不等式的左边是关于n的代数式，右边是关于a的代数式，直接把左边构造成关于n的函数，再利用函数的单调性解决问题.

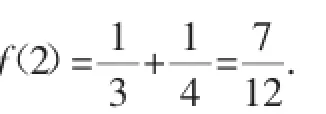
例6（2016年全国普通高考重庆适应性测试（第一次））设f′（x）是函数f（x）的导函数，且f′（x）＞2f（x）（x∈为自然对数的底数），则不等式（flnx）＜x2的解集为（）.

因为f′（x）＞2f（x）（x∈R），所以F′（x）＞0，所以F（x）在（0，+∞）上单调递增.

姊妹题1：设f′（x）是函数f（x）的导函数，满足f′（x）+ 2f（x）＞0，且f（-1）=0，则f（x）＜0的解集为（）.

A.（-∞，-1）B.（-1，1）

C.（-∞，0）D.（-1，+∞）

解析：构造函数g（x）=e2xf（x），由f′（x）+2f（x）＞0，可知g′（x）＞0，即g（x）=e2xf（x）在R上单调递增.由f（-1）=0，得g（-1）=0，则当f（x）＜0时，x∈（-∞，-1）.

姊妹题2：已知f（x）是定义在（0，+∞）上的非负可导函数，且满足xf′（x）-f（x）≤0对任意正数a，b，若a≤b，则必有（）.

A.af（b）≤bf（a）B.bf（a）≤af（b）

C.af（a）≤f（b）D.bf（b）≤f（a）

因为xf′（x）-f（x）≤0，所以g′（x）≤0，即g（x）在（0，+∞）上单调递减.

例7设α＞β＞e（e为自然对数的底数），证明βα＞αβ.

分析：遇到幂函数或指数函数，可考虑先取对数再构造函数.

例8（2015年全国Ⅱ卷21题）设函数f（x）=emx+x2-mx.

（1）证明：f（x）在（-∞，0）上单调递减，在（0，+∞）上单调递增；

（2）若对于任意x1，x2∈［-1，1］，都有|f（x1）-f（x2）|≤e-1，求m的取值范围.

分析：根据特点，先等价变形再构造函数.

解：（1）证明略.

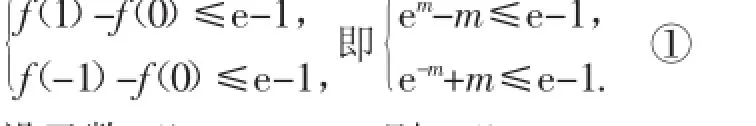
设函数g（t）=et-t-e+1，则g′（t）=et-1.

当t＜0时，g′（t）＜0；当t＞0时，g′（t）＞0.

故函数g（t）在（-∞，0）上单调递减，在（0，+∞）上单调递增.

又g（1）=0，g（-1）=e-1+2-e＜0，故当t∈［-1，1］时，g（t）≤0；

当m∈［-1，1］时，g（m）≤0，g（-m）≤0，即①式成立；

当m＞1时，由g（t）的单调性，知g（m）＞0，即em-m＞e-1；

当m＜-1时，g（-m）＞0，即e-m+m＞e-1.

综上m的取值范围是［-1，1］.

总之，构造函数解不等式问题：一要对问题题型和考点有很好的把握；二要对问题从多角度思考，这就需要我们具备一定的常用的变形处理手段，对问题等价变形，而非改变问题本身.同时构造函数解题自然需要构造函数模型，那么构造怎样的函数模型，利用函数模型的哪些性质来解决问题，需要学生具备联想的思维素质，并且具有一定的思维发散能力.F