一道高三检测试题的命制、解法和教学建议

☉安徽省合肥市教育科学研究院 许晓天

☉安徽省合肥市第一中学吴建平

一道高三检测试题的命制、解法和教学建议

☉安徽省合肥市教育科学研究院 许晓天

☉安徽省合肥市第一中学吴建平

合肥市2017年第二次高三教学质量检测于3月25日至26日进行，理科数学第21题第（2）问引起了教师在各类教研群内广泛讨论.普遍认为此问题的题面与去年高考新课标I卷21题第（2）问相似，但按照高考题提供的解答方法，无法完成此检测试题，这也是此次检测合肥市没有学生完整解答此题的重要原因.下面就此题的命制、解法以及对解题教学谈谈笔者的拙见.

一、试题命制

（一）考题研究

已知函数f（x）=（x-2）ex+a（x-1）2有两个零点.

（1）求a的取值范围；

（2）设x1，x2是f（x）的两个零点，证明：x1+x2＜2.（2016年新课标I理科试题）

解：（1）（解答略）.

（2）不妨设x1＜x2，由（1）知，x1∈（-∞，1），x2∈（1， +∞），2-x2∈（-∞，1），（fx）在（-∞，1）上单调递减.

所以x1+x2＜2等价于（fx1）＞（f2-x）2，即（f2-x2）＜0.

所以（f2-x2）=-x2e2-x2 -（x2-2）ex2

.

设g（x）=-xe2-x-（x-2）ex，则g（′x）=（x-1）（e2-x-e）x.

所以当x＞1时，g（′x）＜0，而g（1）=0，

故当x＞1时，g（x）＜0，

而g（x2）=（f2-x）2＜0，故x1+x2＜2.

研究结论：（1）试题的题目简洁，函数零点、不等式和取值范围都是学生熟知的概念和内容.（2）可以推广为：若f（x1）=f（x2）（x1＜x2），证明：x1+x2＜2.证明：f（x1）＞f（2-x2），也即f（x2）＞f（2-x2），即（x2-2）ex2 +a（x2-1）2＞-x2e2-x2

+ a（1-x2）2，即-x2e2-x2 -（x2-2）ex2

＜0，以下证明相同.

（二）试题命制

命题要求：1.题面尽可能与高考题一样简洁，可以是指数或对数与多项式函数的线性组合；2.第（1）问有分类讨论渗透其中；3.第（2）问命制与题干相关的问题，类似高考题中等函数值点或零点，但要求解法不可以直接仿照高考的方法，要用其他解法，旨在考查学生的创新思维；4.第（2）问不设难度系数，启示教师在二轮复习后期注重学生解题思维和方法的引导，避免按照“题型+方法”的套路进行教学.几易其稿后，最后呈现试题如下：

已知f（x）=ln（x+m）-mx.

（1）求f（x）的单调区间；

（2）设m＞1，x1，x2为函数f（x）的两个零点，求证：x1+ x2＜0.（2017年合肥市高三第二次教学质量检测试题）

二、问题解答

针对第（2）问，命题组提供了两种解答，参考答案只给出了解法一：解法一：（1）（解答略）.

构造函数g（x）=emx-x，则g（x）=emx-x与y=m图像有两交点，交点横坐标为x1，x2，g′（x）=memx-1.

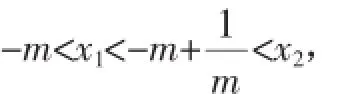
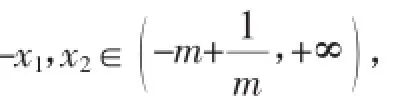
即证明f（-x1）＜0，即ln（-x1+m）+mx1＜0.又f（x1）=ln（x1+m）-mx1=0，所以ln（-x1+m）+ln（x1+m）＜0，即ln（m2-x21＜1.1）＜0.所以0＜m2-x2

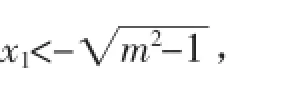
所以g（x）在（1，+∞）上单调递增，故g（m）＞g（1）=0.

故x1+x2＜0成立.

三、教学建议

检测考试结束后，合肥一中吴建平先生提供了第（2）问另外一种证明的方法.

不妨设x1＜x2，则

令m+x1=t1，m+x2=t2，则lnt1=m（t1-m），lnt2=m（t2-m）.

此时欲证明x1+x2＜0，只要证明t1+t2＜2m.

因为lnt1+lnt2=m（t1+t2-2m），且m＞1＞0，

所以只要证明ln（t1t2）＜0，即0＜t1t2＜1.

①若0＜t1＜t2＜1，则由g（t）在（0，1）上单调递减知，（*）式成立，此时0＜t1t2＜1.

②若t2＞t1＞1，则由g（t）在（1，+∞）上单调递增知，（*）式不成立.

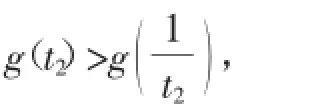
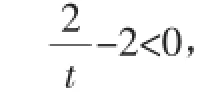
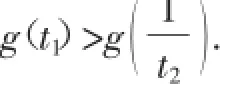
故原命题成立.

其实，证明还有其他方法，这里不再赘述.那么为什么学生在考试的时候，思路就“堵塞”了呢？从学生试卷卷面上发现：许多学生套用去年高考题的做法，终因证得不等式，其不等号方向与欲证明的目标不等式x1+x2＜0的方向不一致而无功而返.这也是许多教师研讨的重点：直接利用原函数证明不行，参考答案提供的是把对数型函数转化为指数型函数，从而顺利解决，为什么这样就可以了呢？针对以上疑问，对今后的教学，特别是高三解题教学提出几点建议：

1.注重内容的本质

由于教师在教学中过度使用“题型+方法”的解题教学方法，特别对高考试题中出现的问题，解题方法的归纳和训练更是细致到位，乃至学生熟练到了“自动化”的程度.因而，考试的时候，学生拿到问题，没有仔细分析，就按照套路做，导致中间过程出现了与套路不同的结果时，考生就无所适从，只好放弃.主要原因是教师教学中没有抓住核心内容的本质，例如，解决此题的主要工具是导数，而导数的本质是判断函数增减性和增减速率.此题抓住了后者——增减速率，此问题就容易解决.本题转化为指数函数的目的：改变定义域上极值点左右的速率，使得极值点右边增加速率大于左边减少速率，从而使得不等号方向改变，达到与所求证不等式x1+x2＜0的方向一致，再证明极值点为负值即可.不仅解题教学需要抓住问题的本质，其他教学，如概念、法则、公式和原理等课型，也要抓住其最本质的要素，这样才能够事半功倍，显著提高教学效率.

2.注重问题的多解

从此题的解答也可以看出，考生利用自己的“经验”在解题，出现了困难时，考生没有办法“另辟蹊径”.也就是说，教师在平时的解题教学中，一题多解做得不够，特别是难度大的问题，一题一解讲清楚就不错了，甚至教师根据学生的实际情况和能力，放弃了难题的解决，这也许是考生在考试中难题丢分的重要原因之一.其实，一题多解不仅能够培养学生能力，而且也是教师解题能力的重要体现.同时，难题的多解产生的思维及方法对容易题的迁移有着不可估量的作用.这就要求教师要历练自己的解题能力，在高三后期的复习中，例如，全国课标卷I的第12、16、20和21题，至少给出两种以上的解法，这样就可以培养学生对问题进行全方位思考的习惯，学生便可以对问题生成多种思考的方式，在一种方法不能够解决时，就立马用另一种方法尝试解决，而不至于出现一种方法受阻就束手无策的现象.

3.注重解题的路径

所谓解题就是在条件和结论之间架起“桥梁”的过程，是由“因为”和“所以”连接起来的逻辑关系链，也就是解题的路径.在教学中让学生自己体悟解决问题的三种思考方式：较容易解决的问题由条件直接推导至结论的“直接法”、较难解决的问题由结论寻求结论成立充分性直至题目条件的“分析法”和由条件推到中间结论与寻求结论成立的中间结论的“两头凑”的方法.对难度较大的问题，大都利用“分析法”或“两头凑”的方法才可以解决.本文的解法二和解法三就是利用“分析法”和“两头凑”寻找解题路径的典范.因此，在解决有一定难度的问题，让学生利用三种思考问题的方式，以期寻找合理的解决路径，直至完整解决问题.

以上是合肥市2017年高三第二次检测理科数学试题21题的命制、特别是第（2）问解答和教学建议，旨让教师在培养学生终生受益的“智力”上下工夫，而非“题型+方法”的机械训练.