圆锥曲线一个定值问题的研究
——2016年高考四川理科卷第20题的进一步探究
2017-05-11于兴江孙玉英
于兴江 孙玉英
山东省聊城市水城中学 (252000) 山东省聊城大学数学科学学院 (252000)
圆锥曲线一个定值问题的研究
——2016年高考四川理科卷第20题的进一步探究
于兴江 孙玉英
山东省聊城市水城中学 (252000) 山东省聊城大学数学科学学院 (252000)
圆的切割线定理是圆的重要性质,本文就2016年四川理科卷第20题做了进一步解析与探究,在一定条件的基础上,现将圆的切割线定理推广到其他常见的圆锥曲线中.
一、原题呈现(2016四川理科卷第20题)
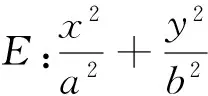
(Ⅰ)求椭圆E的方程及点T的坐标;
(Ⅱ)设O是坐标原点,直线l′平行于OT,与椭圆E交于不同的两点A、B,且与直线l交于点P.证明:存在常数λ,使得|PT|2=λ|PA|·|PB|,并求λ的值.
二、拓展延伸


图1

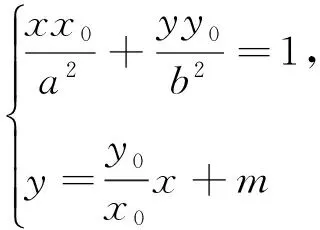

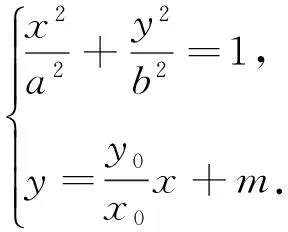

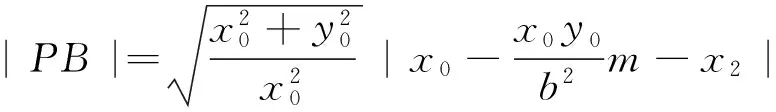

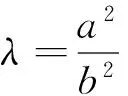
注1:设O为坐标原点,⊙O为x2+y2=a2(a>0),T(x0,y0)是圆上任意一点,过点T(x0,y0)的圆E的切线为l,平行于直线OT的任意直线l′(与OT不重合)与椭圆E交于点A、B,与直线l交于点P.则存在常数λ=1,使得|PT|2=λ|PA|·|PB|.
注2:上述结论1是圆的切割线定理的特殊情况.圆的切割线定理:从圆外一点引圆的切线和割线,切线长是这点到割线与圆交点的两条线段长的比例中项.即若PT切⊙O于点T,PBA是⊙O的割线,则|PT|2=|PA|·|PB|.
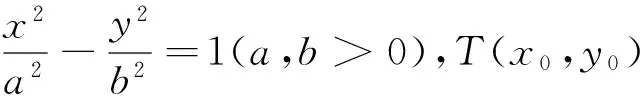
注:证明过程可类比定理1.
定理3 设O为坐标原点,抛物线E为y2=2px(p>0),T(x0,y0)(x0≠0)是抛物线上任意一点,过点T(x0,y0)的抛物线E的切线为l,平行于直线OT的任意直线l′(与OT不重合)与抛物线E交于点A、B,与直线l交于点P.则存在常数λ,使得|PT|2=λ|PA|·|PB|.
注:证明过程可类比定理1.
根据定理1、定理2、定理3综合得到:
定理4 设O为坐标原点,E为圆锥曲线,T(x0,y0)是圆锥曲线上任意一点,过点T(x0,y0)的圆锥曲线E的切线为l,平行于直线OT的任意直线l′(与OT不重合)与圆锥曲线E交于点A、B,与直线l交于点P.则存在常数λ,使得|PT|2=λ|PA|·|PB|.
[1]孙玉英,于兴江.探究引申剖析启示—一道高考题的赏析[J].中学数学研究(江西),2013,10.
[2]柳俊婷,于兴江.2015年山东理科第20题的多解分析及探究[J].中学数学研究(江西),2015,8.
