由一道高考题引发的猜想与证明
2017-05-11李卓祺罗卫强
中学数学研究(江西) 2017年5期
李卓祺 罗卫强
江西省吉安市白鹭洲中学 (343000)
由一道高考题引发的猜想与证明
李卓祺 罗卫强
江西省吉安市白鹭洲中学 (343000)
在平面几何里,有切割线定理:从圆外一点引圆的切线和割线,切线长是这点到割线与圆交点的两条线段长的比例中项.如图1,|PT|2=|PA|·|PB|.

图1
由此进行类比联想,椭圆中是否也有类似于切割线定理的性质呢?
先看一道高考试题:
(1)求椭圆E的方程及点T的坐标;
(2)设O是坐标原点,直线l′平行于OT,与椭圆E交于不同的两点A、B,且与直线l交于点P.证明:存在常数λ,使得|PT|2=λ|PA|·|PB|,并求λ的值.


基于上述结论,可给出以下两个猜想.
猜想1 从椭圆外一点P引椭圆的切线PT与割线PAB,切线长的平方与这点到割线与椭圆交点的两条线段长的积成定比.
猜想2 从椭圆外一点P引椭圆的切线PT和割线PAB,并且此割线平行于切点与椭圆中心的连线,则切线长的平方与这点到割线与圆交点的两条线段长的积成定比.

在不失一般性的前提下,可以给出以下命题:

图2
λ|PA||PB|.




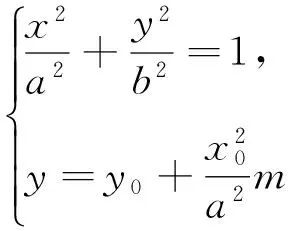

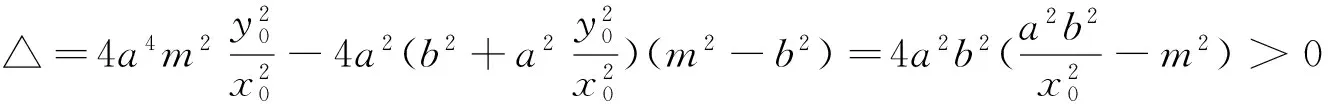


此时λ与m无关,为常数.故命题得证.
这说明椭圆确实具有类似于“圆的切割线定理”的性质.
能否进一步猜想双曲线也具有类似于“圆的切割线定理”的性质呢?有兴趣的读者可尝试探究.
看来解题实践中处处是学问.我们在做题的同时也应该要多多观察题目中的小细节,说不定就能得出有趣的结论.
