基于matlab的常见插值法及其应用

2017-05-09郭小乐

赤峰学院学报·自然科学版 2017年7期

关键词：插值法拉格朗曲线图

郭小乐

（宁夏大学数学统计学院，宁夏银川 750021）

基于matlab的常见插值法及其应用

郭小乐

（宁夏大学数学统计学院，宁夏银川 750021）

本文就数值分析中几种常见的插值法:拉格朗日插值、牛顿插值、Hermite插值及三次样条插值,讨论其不同形式的表达式及误差,结合matlab给出具体实例,对比分析.此外还就三次样条插值的不同计算方法进行归纳、总结.

拉格朗日插值；牛顿插值；Hermite插值；三次样条插值；matlab

1 引言

在许多工程问题中,有时我们只能给出某一函数在一些离散点的值,给不出具体的函数表达式,或者函数的表达式过于复杂不利于计算,这时我们就需要构造这个函数的近似函数,数学上我们把这种方法称为插值[1].插值法作为函数逼近、数值微积分及微分方程数值解的基础,在当今社会被越来越多的学者所关注.尤其随着计算机的普及,很多学者将插值与matlab等软件结合,使得插值法得到了更广泛的应用.

常用的插值法包括：拉格朗日 (Lagrange)插值、牛顿(Newton)插值、Hermite插值、三次样条插值,本文就这四种插值法,结合matlab,从其公式的构造、余项出发,对不同的插值法通过数值实例进行对比研究.此外,还就具有良好收敛性的三次样条函数,归纳出不同的计算方法.

2 几种常见插值法

由于代数多项式具有简单和一些良好的特性,如多项式是无穷光滑的,容易计算它的导数及积分.故本文选择代数多项式作为插值函数.下面依次就这几种插值法进行讨论.

2.1 Lagrange插值

所谓n次Lagrange插值即给定平面上的n+1个互不相同的插值点(xi,f(xi)),i=0,1,2,…,n,利用插值基函数构造唯一的一条次数不高于n次的插值多项式.

2.1.1 n次Lagrange插值多项式形式及误差

拉格朗日插值公式的优点是格式整齐和规范,在理论分析中有重要的价值.它的缺点是没有承袭性质,当需要增加插值节点时,需要重新计算所有的插值基函数,计算繁琐.

2.2 Newton插值

Newton插值是利用差商计算的,下面我们首先给出差商的概念.

定义1[1]设x0,x1,…，xk互不相同,f(x)关于x0,x1,…，xk的k阶差商为

2.2.1 n次Newton插值多项式的形式及误差

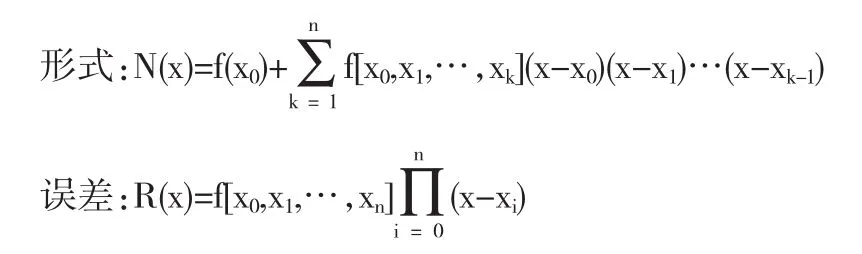
牛顿插值具有拉格朗日插值没有的承袭性,当增加插值节点时,只需再计算一项即可得到相应的插值多项式.由插值多项式的唯一性可知二者是同一插值多项式的不同表达形式.

2.3 Hermite插值

常用Hermite插值描述如下[1]：对于f(x)具有一阶连续导数,以及插值点xi,i=0,1,…,n,xi互不相同,若有至多为2n+1次的多项式函数H2n+1(x)满足：

则称H2n+1(x)为f(x)关于节点{xi}ni=0的Hermite插值多项式.

2.3.1 Hermite插值多项式的形式及误差:

2.4 三次样条插值

在实际计算中,人们很少采用高次插值,其主要原因有两个:其一,由于受到所要通过的插值节点的约束,高次插值描绘的代数曲线是摆动的.即我们常说的Runge(龙格)现象;其二,从计算的舍入误差看,对于等距结点的差分形式,结点上函数值的微小变化可能导致高阶差分的很大变动.故在应用中主要采用的是分段低次插值.实践证明,用分段的低次插值多项式逼近被插函数比在全区间上用高次插值多项式效果好.

一般来说,分段插值所描绘的曲线是不光滑的.为了能获得一条足够光滑的插值曲线,近年来人们采用了分段多项式光滑插值法,即著名的样条函数插值法.本文我们主要介绍具有良好的收敛性,具有二阶光滑性的三次样条插值.

2.4.1 三次样条函数

定义2[5]给定[a,b]上n+1个节点a=x0＜x1＜…＜xn-1＜xn=b以及这些点上的函数值f(xi)=yi(i=0,1,…,n).若函数s(x)满足:

（1）s(xi)=yi,i=0,1,2,…,n；

（2）在每个小区间[xi,xi+1]上是一个次数不超过三次的多项式；

（3）s(x)、s'(x)、s"(x)在[a,b]上都连续.

则称s(x)为函数f(x)关于节点x0,x1,…,xn的三次样条函数.

2.4.2 三次样条插值的几种计算方法

2.4.2.1 利用二阶导数为线性函数求解

令s"(xj)=Mj,j=0,1,…,n.因为s(x)为分段三次多项式,故s"(x)在[xj,xj+1]上是线性函数.可表示为

其中hj=xj+1-xj

为了求出s(x)在[xj,xj+1]上的表达式,需要对上式积分两次,并利用s(xj)=yi及s(xj+1)=yj+1可求出积分常数.得三次样条函数表达式:

再利用光滑连接条件s'(xj-0)=s'(xj+0)，并对s(x)求导得

为了确定唯一的Mj(j=0,1,…,N),补充三个边界条件:

（1）假定s'(x0)=f'0，s'(xn)=f'n；

（2）假定 s"(x0)=f"(x0)，s"(xn)=f"(xn)直接得端点方程M0=f"0，Mn=f"n；

（3）假定M0=MN=0,即为自然边界条件,可得M0=Mn，λnM1+μnMn-1+2Mn=dn；

以上三个边界条件将其写成矩阵形式,得关于Mj(j=0,1,…,n)的三对角线性方程组,利用追赶法[2]求出唯一的Mj(j=0, 1,…,n),将其代入s(x)即可.

2.4.2.2 利用特殊形式的埃尔米特插值公式求解

若插值节点取为xk,xk+1,插值多项式为H3(x),则采用基函数法,

令H3(x)=αk(x)yk+αk+1yk+1+βk(x)mk+βk+1(x)mk+1

其中αk(x)，αk+1（x），βk(x)，βk+1(x)是关于插值节点 xk，xk+1的三次Hermite插值基函数.

上式即为由特殊的埃尔米特插值公式推导的三次样条插值的计算方法之一.

3 数值实例

下图是利用matlab(2012b)编程软件绘制的上述条件下四种不同算法在[0.25,4]插值函数曲线图(a)及其相对误差曲线图(b),直观明了地展示不同插值算法的效果.

图a 插值函数曲线图

从图a中可看出不同插值方法对原函数的逼近效果相差不大.但从图b中的不同插值法的相对误差大小可知,这四种插值方法中,Lagrange插值和Newton插值的效果是一样的,相对另外两种插值方法来说,这两种方法的逼近效果较差,其次是Hermite插值的逼近效果较好,而具有良好收敛性及二阶光滑性的三次样条插值来说,其误差最小,逼近效果最好.