我国城市空气污染数据的准确性判别研究
——基于我国东部三大城市群的比较分析
2017-05-09汤洁茹盖伊蕾
汤洁茹,董 瑶,盖伊蕾
(1.安徽财经大学 金融学院;2.安徽财经大学 统计与应用数学学院,安徽 蚌埠 233030)
我国城市空气污染数据的准确性判别研究
——基于我国东部三大城市群的比较分析
汤洁茹1,董 瑶2,盖伊蕾2
(1.安徽财经大学 金融学院;2.安徽财经大学 统计与应用数学学院,安徽 蚌埠 233030)
本文针对城市空气污染数据的真实性判别及分析问题,以多元线性回归、主成分分析、参数估计、相关分析为研究手段与方法,通过建立多元线性回归模型、各城市群气象数据真实性判定模型、双变量相关分析等模型,得出以下结论:(1)东部三大城市群中,京津冀城市群空气污染数据的准确度低于珠三角与长三角,这可能是由于京津冀极端天气情况较多造成的后果;(2)工业产值与空气质量指标AQI指数、PM2.5、PM10较强的相关性.
城市空气污染;主成分分析;MATLAB;数据分析误判
空气质量问题始终是政府、环境保护部门和全国人民关注的热点问题.2016年的两会上,全国政协常委、环境保护部副部长吴晓青表示,政府工作报告中提出今后五年地级市及以上城市空气质量优良天数比率超过80%的目标必须完成.然而,由于各种主客观原因,会使所采集到的数据序列体现出一定的异常、造假现象.因此对空气污染数据真实性的研究具有一定的现实意义.
1 数据来源与模型假设
京津冀、长三角、珠三角城市群2013年11月1日到2015年2月28日的相关空气污染数据以及苏州市工业产值数据.为了便于解决问题,提出以下假设:(1)假设除了空气污染物含量没有其他因素影响AQI;(2)假设极端天气对空气污染物含量不存在影响;(3)假设若空气污染数据真实,则数据是连续的;(4)假设加入社会因素时,空气质量仅受这一社会因素影响;(5)假设查询的有关城市群社会因素数据是真实有效.
2 空气质量真实性分析
2.1 研究思路
首先我们绘制2015年1月2日到2015年2月28日这一时间段三个城市群AQI指数的变化折线图以判断各城市群AQI指数分布是否一致,若该城市群各指数在同一时刻差异较大则该城市群数据存在误差(或偏误)的现象可能较严重.再以PM10为被解释变量其他指标为解释变量对三个城市群所有城市进行多元线性回归,最后根据线性回归的结果选取残差平方和较大城市.
2.2 数据处理
基于所给数据我们选取2015年1月2日到2015年2月28日这一时间段三个城市群(京津翼、长三角、珠三角城市群)AQI指数的数据,利用MATLAB绘制AQI指数变化折线图,结果如图1、图2、图3所示.
从图2、图3、图4中可以看出京津翼城市群各城市之间AQI指数变化差异较大而长三角城市群和珠三角城市群各城市在这一时段AQI指数波动情况相似且AQI数值较为靠近.因此我们初步判断,京津翼城市群空气质量数据误判的情况相对于其他城市要严重.

图1 京津翼城市群AQI指数变化折线图
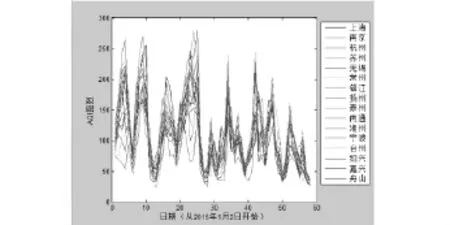
图2 长三角城市群AQI指数变化折线图
以京津翼城市群所有城市不同日期的空气污染数据作为随机变量的原始数据计算相关系数.设变量y、x1、x2、x3、x4、x5分别为 AQI指数、PM2.5浓度、PM10浓度、CO浓度、NO2浓度、SO2浓度,利用EVIEWS得到的相关系数矩阵,如图4.

图3 珠三角城市群AQI指数变化折线图

图4 各变量之间的相关系数矩阵
由图4可知,x2与其余变量的相关性较高均在0.5以上,因此,个地方部门在对数据的误判最有可能是对x2代表的PM10数值进行了错误测算(或者由于极端天气造成数据统计偏误).
以PM10浓度被解释变量,PM2.5浓度、CO浓度、NO2浓度等指标作为解释变量进行多元线性回归并得到相应的误差平方和,如表1.
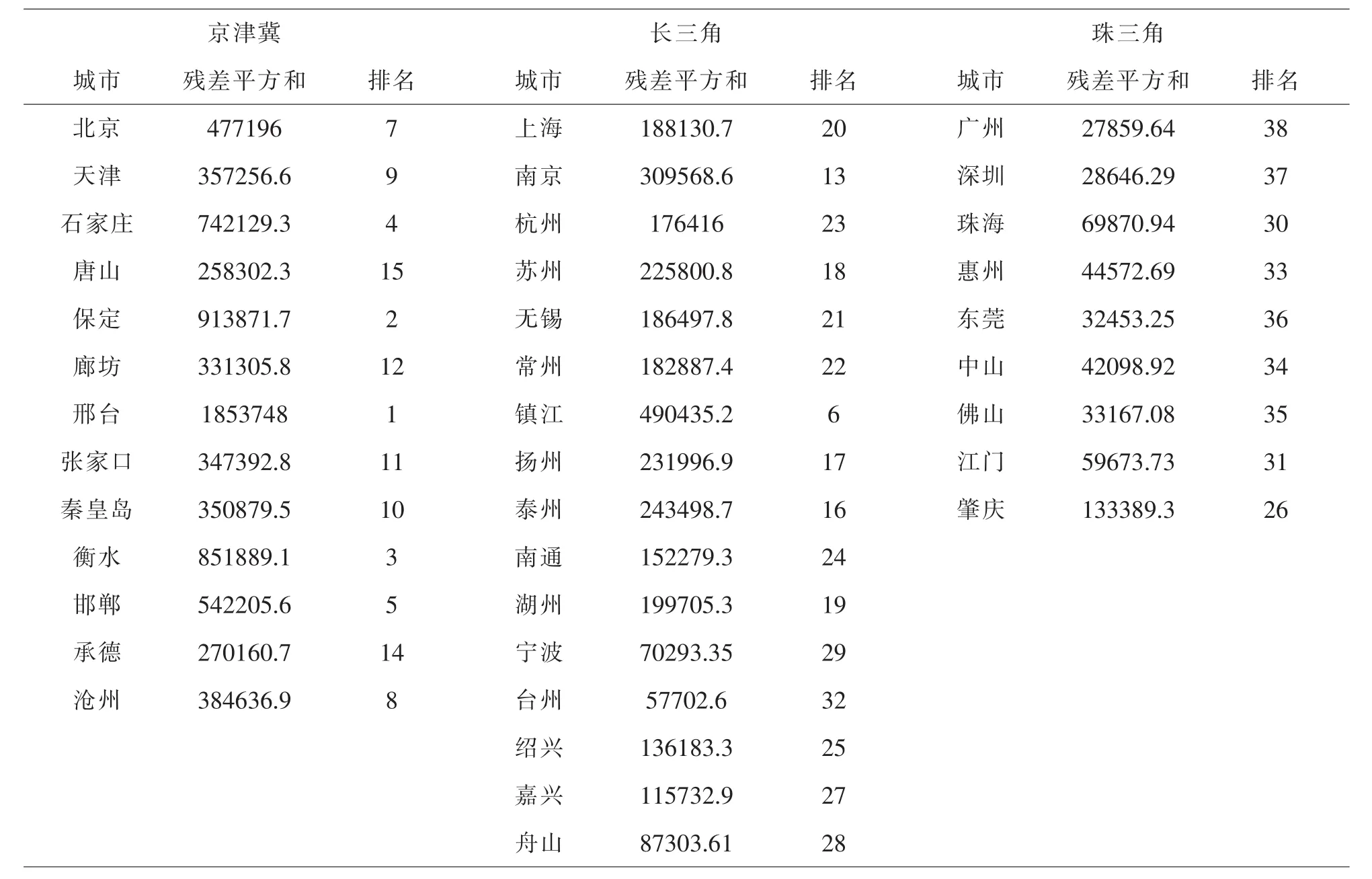
表1 各地回归残差平方和及排名表
2.3 结果分析
由表1可知北京、天津、保定、衡水等城市群残差平方和较大分别为477196、357256.6、913871.7、851889.1,相对于其他城市群的对这些城市群进行多元线性回归时效果并不理想,有可能是由于地方政府获取的PM10数据存在较大误差使x1、x3、x4、x5对x2解释效果变差.
3 各污染物的相关性分析
3.1 研究思路
首先,通过主成分分析选取能够涵盖各污染物所含信息的变量,选取PM2.5,PM10作为主成分,方差累计贡献率可达到91.34%;其次,计算各城市群PM2.5与PM10的相关系数;然后,对这些相关系数进行正态性检验,证明这些相关系数服从正态分布.则在99.73%的置信度下,计算这些相关系数的置信区间,若该城市群的主成分的相关系数不在置信区间内,则说明该城市群数据的真实性或者准确性不足.
3.2 数据处理
毫无疑义,空气的主要污染物变量之间是具有一定的相关关系的.因此,在各个变量之间相关关系研究的基础上,利用主成分分析用较少的新变量代替原来较多的变量,而且使这些较少的新变量尽可能多地保留原来较多的变量所反映的信息.
对各污染物指标变量进行主成分分析:

表2 KMO and Bartlett's检验
由表2可知,各污染物指标变量适合做主成分分析

表3 Communalities分析
由表3、表4可知,为使累计方差贡献率达到85%以上,选取PM2.5和PM10作为主成分,则累计方差率可达到91.343%.
计算各城市群的PM2.5与PM10的相关系数

则可得到各城市群PM2.5和PM10的相关系数,结果见表5.
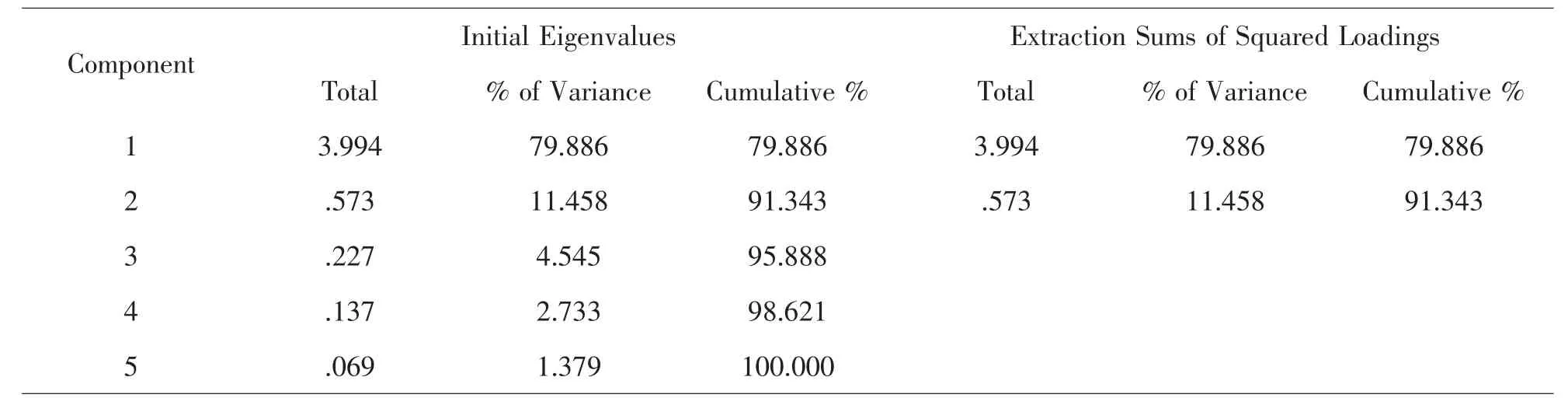
表4 各变量累计贡献率表

表5 各城市群PM2.5和PM10的相关系数表
将这一列相关系数基于SPSS进行正态性检验,结果见表6.
由表6可知,sig值大于0.05,则接受原假设,即这列数据服从正态分布.
3.3 结果分析
这列数据服从正态分布,从而可以计算置信区间.
在置信水平为99.73%下,概率度z=3

表6 Tests of Normality
计算抽样极限误差Δx=zσx=3×0.00694=0.02


在99.73%的置信度下,置信区间为[0.9,0.95],则可知北京,石家庄,唐山,潍坊,邢台城市群的空气质量数据存在不准确的现象.
4 空气质量与工业生产相关性分析
4.1 研究思路
首先我们从苏州市统计局得到苏州市2014年各月的工业产值.其次对数据进行了筛选,由前两问得到的结果我们发现许多工业发达的城市群,都存在信息造假的情况,所以我们选择苏州市的数据进行分析.然后对数据进行处理,取得苏州市2014年各月的工业产值平均值和苏州市2014年各月空气污染指标数据的平均值.最后运用SPSS对变量做双变量相关性分析.
4.2 数据处理
获取数据,对数据进行处理,得到的数据见表7.

表7 苏州市2014年各月工业产值和空气污染数据平均值表
4.3 结果分析
运用SPSS软件得到两两变量的相关系数,见表8.
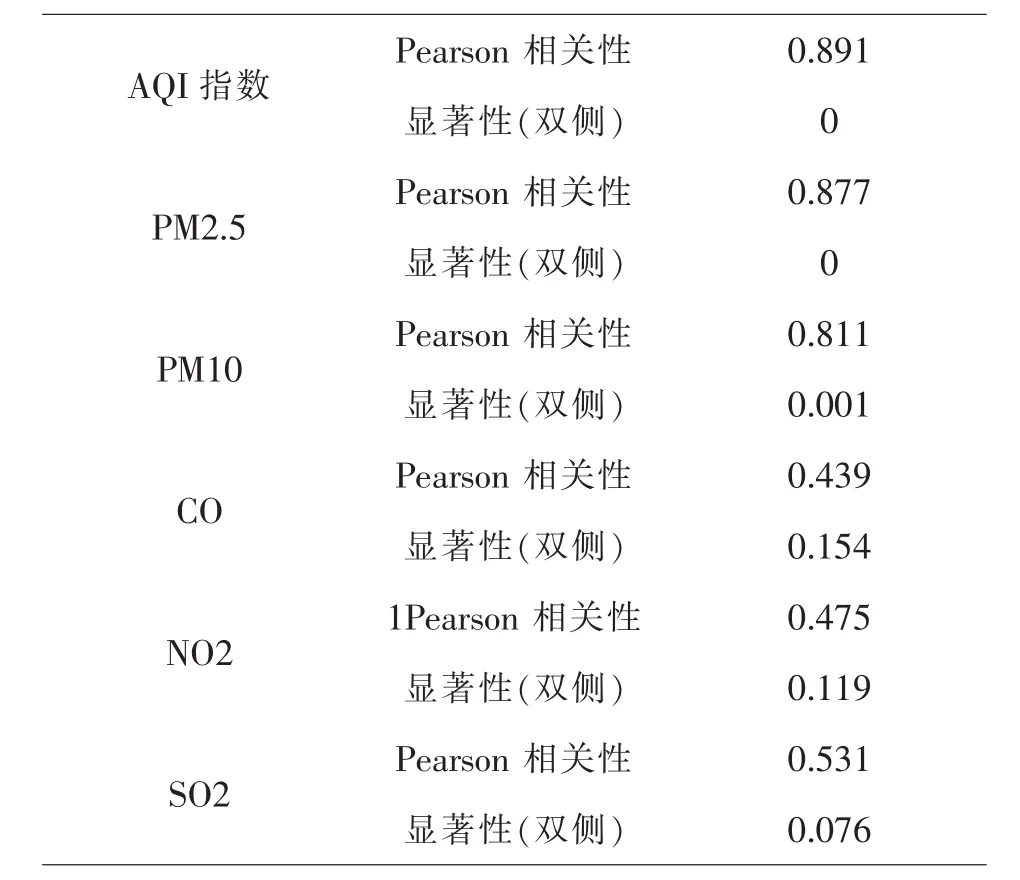
表8 与工业产值相关性分析结果表
由表8可知,AQI、PM2.5、PM10与工业产值的相关系数均接近1,且显著性小于0.05,说明AQI、PM2.5、PM10与工业产值具有很强的相关性.
5 总结
如前所述,研究分析得出,在东部三大城市群中,京津冀城市群空气污染数据的准确度低于珠三角与长三角,这可能是由于京津冀极端天气情况较多造成的后果;与此同时,工业产值与空气质量指标AQI指数、PM2.5、PM10较强的相关性.研究认为,针对有关空气污染数据的准确性问题,综合使用量多种模型和统计方法进行研究,使问题得到更加全面分析,综合使用EVIEWS、SPSS等软件得出各污染数据、工业生产数据的相关性,很好地解决了空气污染数据的准确性判别问题.
〔1〕薛志诚,蔺相如.多元统计分析在评估城市空气污染中的运用[J].电力学报,2009(2):152—153.
〔2〕司守奎,孙玺菁.数学建模算法与应用[M].北京:国防工业出版社,2015.9.
〔3〕吴礼斌,等.经济数学与建模(第二版)[M].北京:国防工业出版社,2013.6.
X51;O13
A
1673-260X(2017)04-0001-04
2016-12-09
