全氮材料基础性能理论研究: Ⅱ.生成焓预测

刘英哲, 来蔚鹏, 尉 涛, 葛忠学, 骆艳娇, 徐 涛, 尹世伟

(1. 西安近代化学研究所 氟氮化工资源高效开发与利用国家重点实验室, 陕西 西安 710065; 2. 陕西师范大学, 陕西 西安 710062)

1 引 言

全氮材料具有能量高、无污染的优点,是潜在的新型高能量密度材料[1-5]。生成焓是评价全氮材料爆轰性能的关键参数。对于稳定化合物,生成焓可由实验方法测得,但全氮材料尚难以获得样品,导致生成焓无法实测。因此,采用理论计算方法成为了获取全氮材料生成焓的主要手段。然而,如何准确可靠地计算全氮材料的生成焓仍然是一个难点。

目前,生成焓的计算方法主要有几下几种: (1)基团加和法、半经验分子轨道法能直接而快速地给出生成焓,但该类方法强烈依赖于参数的准确性,可靠性不强,只能用于生成焓的估算; (2)从头算方法特别是高水平理论方法如QCISD(T),CCSD(T)等能够准确地预测生成焓,但需要巨大的计算资源,只能用于小分子; (3)以Gn及CBS为代表的混合方法具有很高的计算精度,但同样需要较大的计算资源,通常只适用于小分子体系; (4)密度泛函理论能够合理地预测生成焓,且只需较少的计算资源,因此成为当前广泛使用的热门方法,但计算结果强烈依赖于所使用的密度泛函。

本研究基于原子化反应,采用3类9种密度泛函分别对52种多氮化合物的气相标准生成焓进行了计算,通过比较计算值与实验值,筛选出计算精度最高的密度泛函,为全氮材料生成焓预测提供一种合理的方法。

2 计算方法

2.1 数据采集

采集多氮化合物的生成焓数据,包括唑、嗪、叠氮、酯、烷、硝胺、苯胺、硝基胺、硝基苯、腈等52个分子,气相生成焓实验数据取自NIST数据库,见表1。

2.2 生成焓计算

采用密度泛函理论B3LYP/6-31G(d)[6-7]方法对52个多氮化合物进行几何构型优化,经振动频率计算确认所得构型为能量最优。然后,分别采用3类9种不同的密度泛函方法进行生成焓计算,包括(1)单杂化密度泛函B3PW91[8]、B3P86[9]、B3LYP[6-7]、X3LYP[10]和O3LYP[11]; (2)meta杂化密度泛函M052X、M062X和M06HF[12]; (3)双杂化密度泛函B2PLYP[13]。借助原子化反应计算生成焓,以气相分子CaHbNcOd为例,在标准条件下,计算途径如图1所示。

图1基于原子化反应计算生成焓示意图

Fig.1Schematic of atomization reaction route to calculate the enthalpy of formation

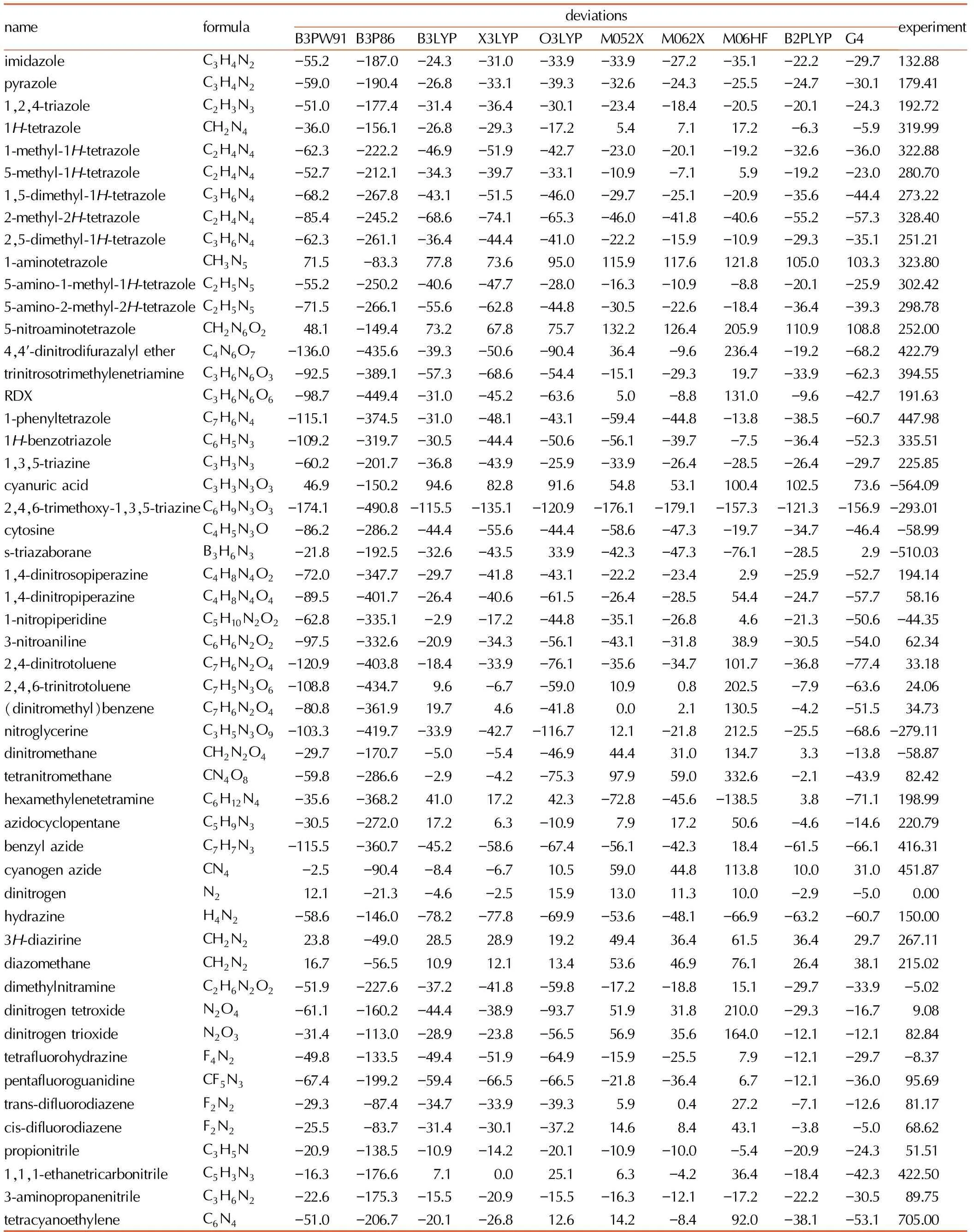
表152个多氮化合物标准生成焓实验值与计算值偏差

Table1Experiment values and deviations of standard enthalpies of formation for 52 nitrogen-rich compounds kJ·mol-1

由图1中的热力学循环可知,CaHbNcOd的气相生成焓ΔfH(CaHbNcOd)可通过下式求解:

ΔfH(CaHbNcOd)=aΔfH(C)+bΔfH(H)+cΔfH(N)+

dΔfH(O)-ΔHatomization

(1)

式中,ΔfH(C), ΔfH(H), ΔfH(N), ΔfH(O)为原子C、H、N和O的实验气相生成焓[14],kJ·mol-1; ΔHatomization为原子化反应的标准反应焓, kJ·mol-1, 通过振动频率分析可获得反应物与产物的焓值,再经由下式计算得到:

ΔHatomization=aH(C)+bH(H)+cH(N)+

dH(O)-H(CaHbNcOd)

(2)

为了更直观地体现各密度泛函的优劣,在焓值计算中没有使用校正因子,并统一使用Dunning基组cc-PVTZ[15-16]进行计算。所有计算均由Gaussian[17]软件完成。

2.3 误差分析

采用平均偏差(MSD)和平均绝对偏差(MAD)评价气相生成焓计算值与实验值的偏离程度,其定义分别如下:

(3)

(4)

式中,ei是计算值与实验值的偏差,n为分子个数,即52。

3 结果与讨论

3.1 密度泛函筛选

基于原子化反应,采用不同密度泛函计算了52个多氮化合物的气相标准生成焓,计算偏差示于表1。为了更客观地评价不同密度泛函的优劣,也采用组合方法G4[18]计算了生成焓。将计算偏差按照化合物顺序作图可得图2,由图2可知,B3P86与M06HF两种泛函显著偏离了其他泛函,计算偏差最大,尤其是B3P86泛函,每个化合物的计算偏差均为负值,说明计算结果存在系统误差。除了B3P86与M06HF,其他方法的计算偏差既有正值也有负值,随机误差可以相互抵消。

为了更准确地评价不同密度泛函的计算结果,计算了52个多氮化合物气相生成焓预测值的平均偏差与平均绝对偏差。如表2所示,M052X、M062X与B2PLYP三个泛函的平均偏差较小,均小于15 kJ·mol-1,说明与实验值吻合较好。其中,以M052X泛函计算最精确。相比之下,B3P86泛函计算结果最差。若进一步区分正、负偏差对计算结果的影响,从平均绝对偏差上看,计算精度最高的前三种泛函分别为B2PLYP、M062X和B3LYP,并且平均绝对偏差均小于G4方法。尽管G4方法在计算小分子原子化能时可以达到化学精度,但并不适用大于10个原子的多氮化合物生成焓计算。因此,最终选择双杂化泛函B2PLYP预测全氮材料的气相标准生成焓。

图2不同密度泛函计算的标准生成焓偏差图

Fig.2Deviations of standard enthalpies of formation for different functionals as a function of compound number

3.2 生成焓预测

笼型全氮因具有较大环张力而备受瞩目。采用B2PLYP泛函对5种笼型全氮分子的气相标准生成焓进行了计算,结果示于表3。由表3可知,笼型全氮具有较高的正生成焓,且随着氮原子数的增加而增加。将B2PLYP的预测结果与其他文献报道的结果进行了比较,包括(1)瑞典国防研究院FOI计算结果[19]; (2)英国QinetiQ公司计算结果[20]。如图3所示,随着氮原子数的增加,B2PLYP计算结果的增长趋势与FOI计算结果类似,但生成焓数据整体偏小。相比之下,QinetiQ计算结果的增长趋势较为平缓。

表2不同密度泛函计算气相生成焓的平均偏差和平均绝对偏差

Table2Mean singed deviations and mean absolute deviations of standard enthalpies of formation for different functionals kJ·mol-1

Note: MSD is mean singed deviation; MAD is mean absolute deviation.

表3笼型全氮分子的气相标准生成焓

Table3Standard enthalpies of formation for representative all-nitrogen molecules with cage type kJ·mol-1

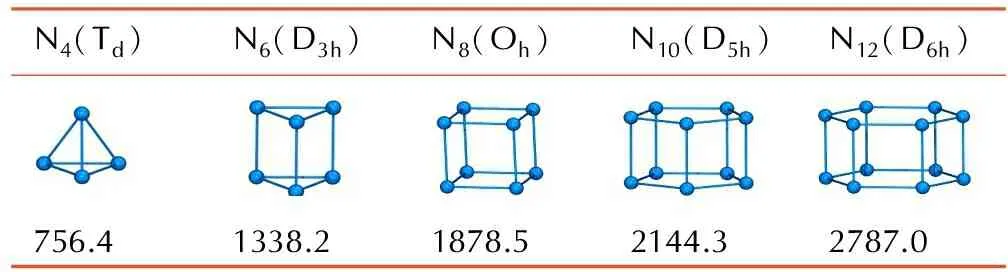
图3生成焓预测值与笼型全氮原子数关系图

Fig.3Predicted enthalpies of formation for all-nitrogen molecules with cage type as a function of nitrogen atom number

通常,在预估含能材料爆轰性能时更关注的是固相生成焓。考虑到气相生成焓的实验数据比固相生成焓多,为了准确评价不同密度泛函的优劣,需采集尽可能多的数据,因此本研究只计算了气相生成焓。至于全氮材料的固相生成焓,可根据本系列论文“Ⅰ.晶体密度预测”[21]中预测的晶体结构进行晶格能计算,从而获得固相生成焓。

4 结 论

(1) 基于原子化反应,通过3类9种密度泛函分别对52种多氮化合物的气相标准生成焓进行了计算,双杂化泛函B2PLYP的计算精度最高,平均绝对偏差为30.1 kJ·mol-1

(2) 采用B2PLYP泛函预测了5种笼型全氮分子N4(Td),N6(D3h),N8(Oh),N10(D5h),N12(D6h)的气相生成焓分别为756.4,1338.2,1878.5,2144.3,2787.0 kJ·mol-1,随着氮原子数目的增加,生成焓逐渐增加。

参考文献:

[1] Eremets M I, Gavriliuk A G, Trojan I A, et al. Single-bonded cubic form of nitrogen[J].NatureMaterials, 2004, 3(8): 558-563.

[2] Samartzis P C, Wodtke A M. All-nitrogen chemistry: how far are we from N60?[J].InternationalReviewsinPhysicalChemistry, 2006, 25(4): 527-552.

[3] Hirshberg B, Gerber R B, Krylov A I. Calculations predict a stable molecular crystal of N8[J].NatureChemistry, 2014, 6(1): 52-56.

[4] 李玉川, 庞思平. 全氮型超高能含能材料研究进展[J]. 火炸药学报, 2012, 35(1): 1-8.

LI Yu-chuan, PANG Si-ping. Progress of all-nitrogen ultrahigh-energetic material[J].ChineseJournalofExplosive&Propellants, 2012, 35(1): 1-8.

[5] 张光全, 董海山. 氮簇合物——潜在的高能量密度材料候选物[J]. 含能材料, 2004, 12(增刊): 105-113.

ZHANG Guang-quan, DONG Hai-shan. Nitrogen clusters—potential candidates as high-energy density materials[J].ChineseJournalofEnergeticMaterials(HannengCailiao), 2004, 12(supple): 105-113.

[6] Lee C, Yang W, Parr R G. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density[J].PhysicalReviewB, 1988, 37(2): 785-789.

[7] Becke A D. Density-functional thermochemistry. III. The role of exact exchange[J].JournalofChemicalPhysics, 1993, 98(7): 5648-5652.

[8] Perdew J P, Wang Y. Accurate and simple analytic representation of the electron gas correlation energy[J].PhysicalReviewB, 1992, 45(23): 13244-13249.

[9] Perdew J P. Density-functional approximation for the correlation energy of the inhomogeneous electron gas[J].PhysicalReviewB, 1986, 33(12): 8822-8824.

[10] Xu X, Goddard III W A. The X3LYP extended density functional for accurate descriptions of nonbond interactions, spin states, and thermochemical properties[J].ProceedingsoftheNationalAcademyofScience, 2004, 101(9): 2673-2677.

[11] Cohen A J, Handy N C. Dynamic correlation[J].MolecularPhysics, 2001, 99(7): 607-615.

[12] Zhao Y, Truhlar D G. The M06 suite of density functionals for main group thermochemistry, thermochemical kinetics, noncovalent interactions, excited states, and transition elements: two new functionals and systematic testing of four M06-class functionals and 12 other functionals[J].TheoreticalChemistryAccounts, 2008, 120(1-3): 215-241.

[13] Grimme S. Semiempirical hybrid density functional with perturbative second-order correlation[J].TheJournalofChemicalPhysics, 2006, 124: 034108.

[14] http:∥webbook.nist.gov/chemistry/2016.01.10.

[15] Head-Gordon M, Pople J A, Frisch M J. MP2 energy evaluation by direct methods[J].ChemicalPhysicsLetters, 1988, 153(6): 503-506.

[16] Kendall R A, Dunning T H, Harrison R J. Electron affinities of the first-row atoms revisited. Systematic basis sets and wave functions[J].TheJournalofChemicalPhysics, 1992, 96(9): 6796-6806.

[17] Frisch M J, Trucks G W, Schlegel H B, et al. Gaussian 09[CP], Gaussian, Inc., Wallingford CT, 2009.

[18] Curtiss L A, Redfern P C, Raghavachari K. Gaussian-4 theory[J].JournalofChemicalPhysics, 2007, 126: 084108.

[19] Östmark H. High energy density materials (HEDM): overview, theory and synthetic efforts at FOI[C]∥New Trends in Research o f Energetic Materials, Czech Republic, 2006: 231-250.

[20] Haskins P J, Fellows J, Cook M D, et al. Molecular level studies of polynitrogen explosives[C]∥12thInternational Detonation Symposium, California, 2002.

[21] 刘英哲, 来蔚鹏, 尉涛, 等. 全氮材料基础性能理论研究:Ⅰ.晶体密度预测[J]. 含能材料, 2017, 25(2): 100-105.

LIU Ying-zhe, LAI Wei-peng, WEI Tao, et al. Theoretical investigations on fundamental properties of all-Nitrogen materials: Ⅰ. Predication of crystal densities[J].ChineseJournalofEnergeticMaterials(HannengCailiao), 2017, 25(2): 100-105.