八年级学生“数学兴趣”“数学自我效能感”“学习坚持性”与“数学成就”的关系研究

杜宵丰，刘 坚



八年级学生“数学兴趣”“数学自我效能感”“学习坚持性”与“数学成就”的关系研究

杜宵丰，刘 坚

（北京师范大学中国基础教育质量监测协同创新中心，北京 100875）

以中国中部某区县23 133名八年级学生为被试，采用结构方程模型考察了中学生数学兴趣、数学自我效能感、学习坚持性与数学成就之间的关系．研究结果表明：（1）数学兴趣、数学自我效能感、学习坚持性对数学成就均有显著正向影响；（2）数学自我效能感可以部分中介数学兴趣与学习坚持性、数学兴趣与数学成就之间的关系；（3）学习坚持性可以部分中介数学兴趣与数学成就、数学自我效能感与数学成就之间的关系．

数学兴趣；数学自我效能感；学习坚持性；数学成就

1 问题提出

近代教育心理学中关于兴趣的研究可以追溯到Herbart时期，他认为兴趣是教育的直接目的，兴趣就是主动性[1]．兴趣可以分为个体兴趣和情境兴趣．个体兴趣是长期形成的并与特定主题或领域有关的一种相对稳定的个体倾向[2]．情境兴趣是由于外部因素刺激而引发的一种或持久或短暂的情感反应[3]．大量研究发现，兴趣在特定内容或领域下对学生的认知表现和情感体验具有积极的促进作用[4~6]．学生对学习“有兴趣”意味着学生的注意力、努力水平、坚持性和活动参与度都会大大增加[7]，并且学习系统和课程材料也会更容易对学生发挥效用[8]．Schiefele、Krapp和Winteler（1992）的元分析发现，学习兴趣与学业成就的平均相关系数为0.30[9]．近年来，虽然没有进一步关于兴趣研究的元分析，但是仍然有很多实证研究聚焦于学习兴趣与动机变量、学业表现之间的关系．杨海波，刘电芝和杨荣坤（2015）发现，学生的数学兴趣可以显著的影响数学自我效能感[10]．Chiu和Zeng（2008）通过PISA数据得出，兴趣与数学成就在大多数国家都具有一致的显著正相关[11]．可见激发学生的学习兴趣是教育教学过程获得成功的重要途径之一．

自我效能感是指人们对其组织和实施达到特定成就目标所需行动过程的能力的信念[12]．根据Bandura的社会认知理论，自我效能感影响个体的认知、动机、情感和决策过程[13]．自我效能感作为重要的动机变量可以帮助解释学生的学习行为和学业表现[14]．具备较高自我效能感的学生愿意接受具有挑战性的任务，加强学习的投入和面对学习困难时的坚持性，能够灵活运用学习策略，并具备较为突出的学习自我调节能力[15~16]，而这些都会对学生的学习活动和学习效果产生积极的影响．研究发现，自我效能感是预测学业成就的一个重要因素，对于学生学业表现的细微变化非常敏感，并且可以作为其它动机因素影响学业成就的中介变量[17~18]．Multon、Brown和Lent（1991）对自我效能感与学业表现的元分析发现，二者之间的平均相关系数为0.38[19]．Robbins等人（2004）对自我效能感影响大学GPA的元分析发现，自我效能感对GPA的平均影响系数为0.496[20]．杨海波等人（2015）的研究表明，自我效能感和学习策略可以有效调节学习兴趣和学业成就之间的关系[10]．可见自我效能感的高低不仅会影响学生的学习表现，同时也是动机结构与学业成就间的一个非常活跃的中介因素．

在学习活动中，个体遇到学习困难与障碍或外界无关刺激影响时坚持努力的程度，即为学习坚持性[21]．研究发现，学习坚持性对学业成就有着重要的影响[22]．Berhenke等人（2011）的研究指出，儿童学习的坚持性与其数学能力、阅读能力的发展有着密切的联系[23]．Oliver和Gottfried（2007）发现，中学生学习的坚持性与专注度可以显著预测当时及其以后的大学成绩，甚至具有比社会经济地位和智力更重要的预测作用[24]．坚持性可以使学生专注于有关学习材料而避免注意力的分散[25]．根据自我调节理论的观点，具有较高自我调节水平的学生能够在学习困难任务上坚持更长的时间，通过主动调节努力水平和认知策略来保证学习质量[26]．可见学习坚持性反映了个体有效自我管理和自我调控学习行为的能力，是教育教学获得成功的重要因素．此外，当今大部分的动机理论认为，人们产生和坚持行为的程度与他们相信行为将导致渴望的结果或目标相关．在自我调节学习过程中学习兴趣和自我效能感是影响学习坚持性的重要动机变量[27]．这预示着学习兴趣与自我效能感可以通过学习坚持性的中介作用对学业成就产生影响．

综合上述研究不难发现，学习兴趣、自我效能感、学习坚持性和学业成就是密切关联的变量，但以往的研究较少在数学学科领域将学习兴趣、自我效能感、学习坚持性和学业成就综合在一起来考察，且大多采用相关分析和回归分析的手段探讨各变量之间的关系．因此有必要综合分析数学兴趣、数学自我效能感、学习坚持性和数学成就之间的内在关系机制．通过对以往研究的梳理，研究者提出如下研究假设．

H1：数学兴趣、数学自我效能感、学习坚持性对数学成就有显著正向影响；

H2：数学自我效能感可以部分中介数学兴趣与学习坚持性、数学兴趣与数学成就之间的关系；

H3：学习坚持性可以部分中介数学兴趣与数学成就、数学自我效能感与数学成就之间的关系．

上述假设H1、H2、H3组合成为该研究的假设模型（hypothetical model），如图1所示．在这个假设模型中，数学兴趣为自变量，数学成就为因变量，数学自我效能感和学习坚持性构成中介变量．在研究工具设计、数据收集的基础上，运用结构方程模型（Structure Equation Model, SEM）的方法来分析这一假设模型是否成立．

图1 假设模型

2 研究方法

研究基于北京师范大学中国基础教育质量监测协同创新中心“区域教育质量健康体检”项目．针对八年级学生的数学学业水平进行了测试，同时采用问卷的方法了解影响学生数学学习的因素．

2.1 研究对象

研究全样本选取中国中部某区县的23 133名八年级学生作为测试对象．学生样本来源情况详见表1．

表1 学生样本情况

2.2 测量工具

（1）学生问卷．

在借鉴国外大规模学业成就测验背景因素调查内容的同时，由数学教育科研专家、教学一线优秀教师及心理与教育测量专业专家等经过多次论证，对学生进行深度访谈，初步形成基本框架后进行编制，后经过300人预测试、数据分析、问卷修订、专家审议等环节而形成．研究设计问卷采用5级Likert量表形式，数学兴趣和学习坚持性的题目从“非常不同意”到“非常同意”，记为1~5分，数学自我效能感的题目从“非常困难”到“非常容易”，记为1~5分，每个题项只能选择一个答案．

数学兴趣量表，共计4道题目，分别是：“我喜欢阅读数学类的读物”、“我很喜欢上数学课”、“我做数学题时，经常感到很快乐”、“我对数学很感兴趣”．数学兴趣的Alpha（Cronbach）信度为0.934．数学自我效能感量表，共计5道题目，分别是：“根据购买商品的数量和单价来比较、计算两种优惠方案中哪种更合算”、“求出方程的解，例如：3+5=17”、“用两种方式来测量大树的高度”、“将不等式的答案在数轴上表示出来”、“利用扑克牌设计一个公平的游戏”．数学自我效能感的Alpha（Cronbach）信度为0.910．学习坚持性量表，共计3道题目，分别是：“我给自己定的学习计划，经常因为自己不坚持学习而不能如期完成”、“上课时，我有时忍不住去和同学说话或干别的事情”、“我经常设定一个学习目标，但后来又会改变”．由于学习坚持性量表的题目均为反向题，因此在数据分析过程中首先对其进行反向计分，学习坚持性的Alpha（Cronbach）信度为0.667．问卷量表均符合目前一般学者认为信度宜大于0.6以上的最小值要求[28]，因此，该问卷工具拥有良好的内部一致性信度．

（2）数学学业测试卷．

测试试卷以国家颁布的《义务教育数学课程标准（2011年版）》为依据，测试框架分为内容领域（数与代数、图形与几何、统计与概率）和能力维度（了解、理解、应用）两个方面．试题注重考察学生对核心内容的理解和掌握，兼顾覆盖率，有难度的题目主要考察学生高层次认知能力．按照国际通行的教育测量程序，测试试卷先后经历了6人访谈，30人小规模测试，300人大规模测试，外审机构的独立评审等环节命制而成．运用项目反应理论（Item Response Theory）技术求得学生的数学能力值，并将其转化成均值为500，标准差为100的量尺分数．测试卷的Alpha（Cronbach）信度为0.904，说明测试工具拥有良好的内部一致性信度．

（3）数据分析．

研究使用SPSS20.0和MPLUS7.11进行数据的统计分析和模型的验证．首先在MPLUS7.11软件中对数学兴趣、数学自我效能感、学习坚持性进行整体的验证性因素分析（Confirmatory Factor Analysis, CFA），证明模型中各潜变量与观测变量具有良好的测量结构．然后在SPSS20.0软件中利用Pearson相关分析检验各变量维度间的相关关系，并通过回归分析检验各变量的多重共线性．最后采用结构方程模型的方法对假设模型进行分析计算，检验假设模型的拟合度，分析各潜变量之间的关系．

3 研究结果

3.1 验证性因素分析

验证性因素分析用来检验量表的结构效度，从而系统保证研究工具的质量．采用MPLUS7.11软件对测试结果进行验证性因素分析（CFA），结果发现：卡方值=3 041.383，<0.001；渐进残差均方和平方根=0.051；相对拟合指标=0.984，=0.979，=0.036．结果显示，各测量维度具有较好的模型拟合度．数学兴趣、数学自我效能感、学习坚持性的因素载荷量位于0.617和0.935之间（详见表2），都高于0.600，表示测量指标能够较好地反映潜在变量的特质．以上数据说明，所设计的问卷内在质量是理想的．

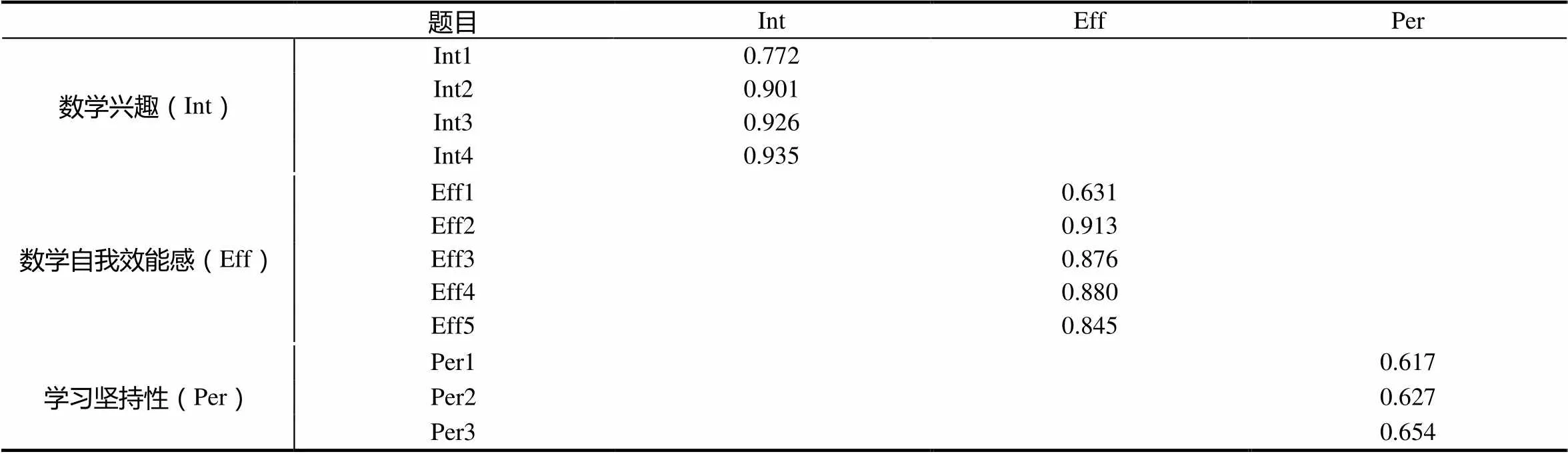
表2 各个变量的因素载荷

3.2 描述统计和相关分析

研究采用SPSS20.0软件分析数学兴趣、数学自我效能感、学习坚持性和数学成就的平均值和标准差，并对各变量间的相关关系进行检验．如表3所示，数学兴趣与数学自我效能感（=0.415，<0.01）、学习坚持性（=0.164，<0.01）、数学成就（=0.333，<0.01）呈显著正相关关系，数学自我效能感与学习坚持性（=0.154，<0.01）、数学成就（=0.468，<0.01）呈显著正相关关系，学习坚持性与数学成就（=0.182，<0.01）呈显著正相关关系．数据结果表明，数学兴趣、数学自我效能感、学习坚持性对数学成就有显著正向影响，因此假设H1被接受．数学兴趣、数学自我效能感、学习坚持性的方差膨胀因子（Variance Inflation Factor, VIF）分别为1.221<10、1.216<10、1.039<10，因此各变量不存在多重共线性．

表3 变量间的相关系数和描述统计

注：*. 在0.05水平（双侧）上显著相关；**. 在0.01水平（双侧）上显著相关

3.3 假设模型的SEM检验结果

验证性因素分析及信度分析结果表明，所设计的问卷调查结构与实际数据的拟合度较好，适合对假设模型作进一步的结构方程模型（SEM）检验．结构方程模型使用最大似然估计的方法，计算结果如图2所示．其中，卡方值=3 895.466，<0.001；渐进残差均方和平方根=0.053；相对拟合指标=0.980，=0.974，=0.035．说明SEM模型拟合良好，假设模型可以被接受．

图2 理论模型

从图2可以看出，数学兴趣可以显著预测数学成就（=0.167，<0.001），并且显著影响数学自我效能感（=0.424，<0.001）和学习坚持性（=0.157，<0.001）；数学自我效能感可以显著预测数学成就（=0.392，<0.001)，并且显著影响学习坚持性（=0.117，<0.001）；学习坚持性可以显著预测数学成就（=0.119，<0.001）．因此，假设H1再次得到证实．为了进一步检验数学自我效能感和学习坚持性的中介效应，运用采样次数为1 000的bootstrap方法的非对称置信区间对中介效应进行显著性检验，如果间接效应的95%的置信区间不包含零，则代表间接效应是显著的．Bootstrap检验结果表明，数学自我效能感在数学兴趣和数学成就之间发挥显著的部分中介效应（95% CI: 0.158, 0.175）；数学自我效能感在数学兴趣和学习坚持性之间发挥显著的部分中介效应（95% CI: 0.041, 0.059）；学习坚持性在数学兴趣和数学成就之间发挥显著的部分中介效应（95% CI: 0.015, 0.022）；学习坚持性在数学自我效能感与数学成就之间发挥显著的部分中介效应（95% CI: 0.011, 0.017）．由上述结果可知，H2、H3皆获得支持．SEM模型中各变量间的直接效应和间接效应详见表4．

表4 SEM模型的标准化效应结果

4 结论与讨论

研究发现，数学兴趣、数学自我效能感和学习坚持性对数学成就都有显著的正向影响．根据自我决定理论，通过激发内部兴趣可以使个体感知自身心理需要和外部环境因素的联系机制，并在该环境下能够充分地体现其自我认可的价值，形成个人主动学习的冲动，这种内在驱动力会促进个体的心理成长和认知发展[29]．近二十多年来的研究也都证实，兴趣高的学生会对所学内容建立更多的联系和进行更多的独立思考，对所获得的知识具有更高的迁移水平和推理能力[30]．Bandura的自我效能感理论认为，人们的目的性行为受到预期目标的调节，而预期目标的设定则受到自我效能感的影响，自我效能感越强的学生，为自己设定的学习目标越高，承担责任越坚定，其学业成就水准也越高[31]．青少年时期是个体坚持性开始发展并产生积极影响的关键时期[32]．根据自我调节学习理论，面临学习困难和障碍时，能坚持下去的学生，会付出更多的努力和倾注更多的情感，能有效地对自己的学习活动进行调节和监控，从而保证学习的质量和效果[33]．研究进一步发现，数学自我效能感可以部分中介数学兴趣与学习坚持性、数学兴趣与数学成就之间的关系．自我效能感是动机结构中重要的中介因素，可以有效调节学业成就、学习行为以及其他情感和动机现象[34]．学习兴趣与自我效能感关系紧密，一项关于学习兴趣和自我效能感关系的元分析表明，二者间的平均相关程度达到0.59[35]．Bandura（1995）认为，学习兴趣作为一种内在因素会影响学生自我效能信念的发展[36]．自我调节学习理论的观点也说明，具有较高兴趣的个体会投入更多的时间和精力去完成具有挑战性的任务，而成功体验是自我效能感的重要来源之一，因此在自我调节学习过程中兴趣会导致个体产生完成任务的自我效能[37]．学习兴趣会带动学生的学习动力与愿望，学生学习数学的兴趣越强，学习数学的热情就越强烈，对数学学习也更为有自信，从而促使学生以更为积极的态度，通过努力和坚持，最终实现学习目标[38~39]．最后，学习坚持性可以部分中介数学兴趣与数学成就、数学自我效能感与数学成就之间的关系．兴趣和自我效能感是自我调节学习理论的各社会认知模型中的重要动机信念，动机信念是引起和维持个体活动，并使该活动指向某一目标的内部动力或过程．研究显示，以自我效能感为基础的学习动机能够促使学生在遇到困难时通过对学习意图、努力程度及坚持性的主动控制来确保目标的达成[40]．也有研究指出，长期目标或当目标变得不坚定时，其对行为的作用会受到干扰，这时候个体所体验到积极的兴趣是使行为得以继续的重要因素，体验到的兴趣对于行为的启动与坚持性以及个体保持努力以达成目标有重要的作用[41]．

从理论模型的标准化效应结果来看，数学自我效能感对数学成就的总体影响效应最大，数学兴趣其次，学习坚持性再次．数学自我效能感对数学成就的影响主要来自直接影响，而数学兴趣对数学成就的间接影响大于直接影响．这一结果说明数学兴趣与数学自我效能感、学习坚持性的内在联系更为紧密，而自我效能感与数学成就的联系更为紧密．不难理解，学生的自我效能感主要建立在作为能力指标的掌握经验，通过能力传递形成的替代经验，知道自己拥有某些能力的言语说服，以及用于判断自身能力的情绪状态之上，因而对学习能力或成就表现有着更为直接和显著的影响．而即使学生对数学有较高的兴趣，但若对自己是否能成功的学习没有自信或对学习任务的坚持性不足，那么当他遇到困境或感到倦怠时很难做出适当的自我调节，进而影响数学成就的发展．此外，学习坚持性对数学成就的直接效应不高，可能原因是在中国应试教育的大背景下，学生的一部分学习坚持性受到外在因素的影响，比如巨大的学业负担和竞争压力，再比如中国传统文化中孔子伦理观念十分强调学习上的优秀．这些外在因素迫使学生单纯的依靠努力程度来坚持学习，但缺乏一定的自我调节机制，因而只能发挥有限的影响．

综上可知学习动机既能直接作用于学业成就，又能通过动机间的转化和对学习行为的影响间接地作用于学业成就．因此在教育教学中既要重视学生学习意志品质的培养，即是否坚持学，又要注意提高学生学习数学的兴趣和自信，即是否主动学．坚持学不是单纯增加努力程度，必须使学生认识或体会到学习的内在价值和乐趣，引导学生通过对于学习的积极态度和情感体验来有效调节和监控自己的学习活动；主动学是中国数学课程改革倡导的新理念，传统教学忽视学生本身的能动性，把学生看作被动的接受者而非主动参与者，所以应该将学生从被动接受知识的方式中解放出来，转向主动理解知识、主动参与数学活动、主动探索并建构自己的学习历程．

5 研究意义与研究局限

研究的结果具有一定的教育实践意义，有助于理解影响中学生数学成就的因素和机制，并帮助教育工作者了解从哪些途径提升学生的数学成就．根据研究的结果，数学兴趣、数学自我效能感、学习坚持性对数学成就有着重要的影响．但目前，中国的学校教育对学生的学习动机没有足够的关注，原因是多方面的，其中一个重要原因是在应试教育、片面追求升学率的影响下，中小学生的学习被看作是取得良好考试分数的工具，这使学生不能形成较强的学习动机，对学习缺乏兴趣和自信．因此教师在日常教学活动中，应当适当给予学生肯定、鼓励等情感支持或提供实质性的反馈或帮助，尽可能挖掘学生的长处，为学生创造更多的表现机会和成功机会，提升学生的数学自我效能感．同样，在教育中注重课堂的生动性、连贯性、理解性，为学生设置合适的学习目标，提供适宜的挑战性任务，注重学生数学活动经验的积累，给予学生更多的选择权和自主性，从而改善学生数学学习的兴趣水平，激发学生学习的主动性、积极性和坚持性，最终达到促进学生学业发展的目的．

研究也存在一定的局限性．首先，问卷数据采用自我报告的形式，因此数据结果的可信度依赖于学生的诚实作答，进一步收集访谈和观察等综合数据是未来研究需要关注的地方；其次，仅考虑了数学兴趣、数学自我效能感、学习坚持性对数学成就的影响机制，缺乏更为丰富的动机结构，比如数学自我概念、工具型动机等，这些因素在中国教育的背景下对数学成就的影响机制有待深入分析．

[1] 何旭明．学习兴趣的唤起——教师的教育教学对学生学习兴趣的影响研究[M]．北京：教育科学出版社，2011．

[2] Schiefele U. Interest, Learning, and Motivation [J]., 1991, 26(3-4): 299-323.

[3] Krapp A. Structural and Dynamic Aspects of Interest Development: Theoretical Considerations from an Ontogenetic Perspective [J]., 2002, 12(4): 383-409.

[4] Krapp A. Basic Needs and the Development of Interest and Intrinsic Motivational Orientations [J]., 2005, 15(5): 381-395.

[5] Hidi S, Harackiewicz J M. Motivating the Academically Unmotivated: A Critical Issue for the 21st Century [J]., 2000, 70(2): 151-179.

[6] Hidi S, Renninger K A. The Four-Phase Model of Interest Development [J]., 2006, 41(2): 111-127.

[7] Hidi S. An Interest Researcher’s Perspective on the Effects of Extrinsic and Intrinsic Factors on Motivation [A]. In: Sansone C, Harackiewicz J M.[C]. Academic Press, 2000.

[8] Rotgans J I, Schmidt H G. Situational Interest and Learning: Thirst for Knowledge [J]., 2014, (32): 37-50.

[9] Schiefele U, Krapp A, Winteler A. Interest as A Predictor of Academic Achievement: A Meta-Analysis of Research [A]. In: Renninger A, Hidi S, Krapp A.[C]. Psychology Press, 2014.

[10] 杨海波，刘电芝，杨荣坤．学习兴趣、自我效能感、学习策略与成绩的关系——基于Kolb学习风格的初中数学学习研究[J]．教育科学研究，2015，（10）：52-57．

[11]  Chiu M M, Xihua Z. Family and Motivation Effects on Mathematics Achievement: Analyses of Students in 41 Countries [J]., 2008, 18(4): 321-336.

[12]  Bandura A. Self-efficacy: The Exercise of Control [J]., 1999, 604(2): 158-166.

[13]  Bandura A. Social Cognitive Theory in Cultural Context [J]., 2002, 51(2): 269-290.

[14]  Schunk D H. Self-efficacy and Achievement Behaviors [J]., 1989, 1(3): 173-208.

[15]  Carmichael C, Taylor J A. Analysis of Student Beliefs in A Tertiary Preparatory Mathematics Course [J]., 2005, 36(7): 713-719.

[16]  Pajares F. Self-Efficacy Beliefs, Motivation, and Achievement in Writing: A Review of the Literature [J]., 2003, 19(2): 139-158.

[17]  Zimmerman B J. Self-Efficacy: An Essential Motive to Learn [J]., 2000, 25(1): 82-91.

[18]  Pajares F. Self-Efficacy Beliefs in Academic Settings [J]., 1996, 66(4): 543-578.

[19] Multon K D, Brown S D, Lent R W. Relation of Self-Efficacy Beliefs to Academic Outcomes: A Meta-Analytic Investigation [J]., 1991, 38(1): 30-38.

[20] Robbins S B, Lauver K, Le H, et al. Do Psychosocial and Study Skill Factors Predict College Outcomes? A Meta-Analysis [J]., 2004, 130(2): 261-288.

[21] 张林，张向葵．中学生学习策略运用、学习效能感、学习坚持性与学业成就关系的研究[J]．心理科学，2003，（4）：603-607．

[22] 魏军，刘儒德，何伊丽，等．小学生学习坚持性和学习投入在效能感、内在价值与学业成就关系中的中介作用[J]．心理与行为研究，2014，（3）：326-332．

[23]  Berhenke A, Miller A L, Brown E, et al. Observed Emotional and Behavioral Indicators of Motivation Predict School Readiness in Head Start Graduates [J]., 2011, 26(4): 430-441.

[24] Oliver P H, Guerin D W, Gottfried A W. Temperamental Task Orientation: Relation to High School and College Educational Accomplishments [J]., 2007, 17(3): 220-230.

[25] Velting O N, Whitehurst G J. Inattention-hyperactivity and Reading Achievement in Children from Low-Income Families: A Longitudinal Model [J]., 1997, 25(4): 321-331.

[26]  Duckworth A L, Carlson S M. Self-Regulation and School Success [A]. In: Sokol B W, Grouzet F M E, Müller U.[C]. Cambridge University Press, 2013.

[27]  Holmquist C L.[D]. Johnson & Wales University, 2013.

[28]  Hair J F, Black W C, Babin B J, et al.[M]. New Jersey: Pearson Education, 2006.

[29] 王婷婷，庞维国．自我决定理论对学生学习自主学习能力培养的启示[J]．全球教育展望，2009，（11）：40-43．

[30] 章凯，张必隐．兴趣对文章理解的作用[J]．心理科学，2000，（4）：482-483．

[31]  Bandura A, Wood R. Effect of Perceived Controllability and Performance Standards on Self-Regulation of Complex Decision Making [J]., 1989, 56(5): 805-814.

[32]  Padilla-Walker L M, Day R D, Dyer W J, et al. “Keep on Keeping On, Even When It’s Hard!” Predictors and Outcomes of Adolescent Persistence [J]., 2013, 33(4): 433-457.

[33] 魏军，刘儒德，何伊丽，等．小学生学习坚持性和学习投入在效能感、内在价值与学业成就关系中的中介作用[J]．心理与行为研究，2014，（3）：326-332．

[34]  Rahmati A, Moradpour S. Investigation of Relationship between Academic Self-Efficacy and Mathematics Achievement Evaluation of Students Using Summative Evaluation [J]., 2016, 1(1): 872-879.

[35]  Rottinghaus P J, Larson L M, Borgen F H. The Relation of Self-Efficacy and Interests: A Meta-analysis of 60 Samples [J]., 2003, 62(2): 221-236.

[36]  Bandura A. Comments on the Crusade Against the Causal Efficacy of Human Thought [J]., 1995, 26(3): 179-190.

[37]  Ainley M, Buckley S, Chan J. Interest and Efficacy Beliefs in Self-regulated Learning: Does the Task Make A Difference [A]. In: Wosnitza M, Karabenick S, Efklides A, et al.[C]. Hogrefe Publishing, 2009.

[38] 张芳全．家长教育程度、文化资本、自我抱负、学习兴趣与数学成就之关系研究[J]．台中教育大学学报，2011，（1）：29-56．

[39] Wentzel K R, Wigfield A. Academic and Social Motivational Influences on Students' Academic Performance [J]., 1998, 10(2): 155-175.

[40]  Bandura A. Human Agency in Social Cognitive Theory [J]., 1989, 44(9): 1 175-1 184.

[41] 王婷婷．自我调节学习过程中的动机研究[D]．华东师范大学，2008．

[责任编校：周学智]

Study of the Relationships among Mathematics Interest, Mathematics Self-Efficacy, Learning Persistence, and Mathematics Achievement on Grade Eight

DU Xiao-feng, LIU Jian

(Collaborative Innovation Center of Assessment toward Basic Education Quality, Beijing Normal University, Beijing 100875, China)

This study aimed to examine the relationships among mathematics interest, mathematics self-efficacy, learning persistence, and mathematics achievement by the Structure Equation Modeling with 23 133 eight graders from middle district of China. The results indicated that: (1) Mathematics achievement was significantly predicted by mathematics interest, mathematics self-efficacy, and learning persistence respectively; (2) Mathematics self-efficacy could partially mediate the relationship between mathematics interest and learning persistence, as well as the relationship between mathematics interest and mathematics achievement; (3) Learning persistence could partially mediate the relationship between mathematics interest and mathematics achievement, as well as the relationship between mathematics self-efficacy and mathematics achievement.

mathematics interest; mathematics self-efficacy; learning persistence; mathematics achievement

G632

A

1004–9894（2017）02–0029–06

2016–12–10

北京师范大学中国基础教育质量监测协同创新中心区域教育质量健康体检项目——中学数学学业质量诊断与反馈（105006）

杜宵丰（1989—），男，河南安阳人，博士生，主要从事数学教育研究．