小学生近似数量表征系统和工作记忆与数学成绩的关系

孔海燕，孙 雨，宋广文



小学生近似数量表征系统和工作记忆与数学成绩的关系

孔海燕1，孙 雨2，宋广文3

（1．鲁东大学教育科学学院，山东烟台 264025；2．曲阜师范大学教育科学学院，山东曲阜 273165；3．华南理工大学心理测评与应用心理学研究所，广东广州 516041）

数学学习过程中需要很多认知活动的参与，通过测试小学生的近似数量表征能力、工作记忆情况，探讨它们与数学学习成绩的关系．结果表明：小学生的近似数量表征能力和工作记忆能力有一定的可塑性，会随着年龄的增长而提高，并对数学成绩有促进作用，学校的数学教育在这个过程中功不可没．近似数量表征能力与工作记忆可以在不同程度上预测儿童的数学成绩．

小学生；近似数量表征系统；工作记忆

无论在日常生活还是学校学习中，数学的地位都非常重要．数学能力作为一种高级的认知能力在儿童身上的发展变化规律值得探讨．表征是信息在头脑中的呈现方式，根据信息加工理论的观点，当有机体对外界信息进行加工（输入、编码、转换、存储和提取等）时，这些信息以表征的形式在头脑中出现．同一事物，其表征方式不同，对它的加工也不相同[1]．数量表征（numerical representation）指个体心理对数量刺激的解释、表达与操作的过程，从静态的角度分析，它是指主体理解数量概念及其关系的概念系统，主体对数量意义的理解并非只是孤立地理解特定量的大小，而是要会建构一种量与量之间的复杂关系网络；从动态的角度分析，数量表征是指个体头脑内部对数量刺激的解释表达与操作过程[2]．综合已有研究可发现，数量表征系统有不同的分类，例如，从表征依赖的对象上可分为非符号数量表征系统和符号数量表征系统，非符号数量表征是指个体不需要依赖符号知识对视觉、听觉或跨信道呈现的实物或实物记号的数量刺激进行表达和运算的过程，具有一定的种系进化基础，先于语言发生，常常通过点集异同任务、点集比较任务、点集加减法任务等考察；符号数量表征是指依赖于符号知识对数字和数词等形式的数量进行表征的过程，常用数字比较任务等测查[3]．从表征的准确程度上可分为精确数量表征系统（Exact Number System，ENS）和近似数量表征系统（Approximate Number System，ANS），前者是对小数（自然数1~3或4）的精确表征，后者是对大数（≥4的自然数）的近似表征或模拟幅度表征[4]．

工作记忆是个体在认知学习时的重要角色，在数学学习中的地位更是举足轻重．它是用来加工和存储与之相关信息的、能量有限的机制，包括中央执行系统（central executive system）、语音环路（phonological loop）和视觉空间模板（visual-spatial sketchpad）3部分：中央执行系统负责工作记忆中的注意控制，其功能类似于一个能量有限的注意系统，该系统负责指挥下一级系统的活动，是工作记忆模型的核心，它可以集中加工目标信息、抑制无关干扰、监控能量分配、协调各系统的联系；视觉空间模板负责对视觉图像信息（比如颜色、形状等元素）和空间信息（比如方位、位置等元素）进行加工；语音环路负责贮存与复述言语信息，包括语音储存和发音控制加工两个子成分．关于数学认知的研究有两种解释途径：一般的观点认为，个体非数字的认知能力如工作记忆、长时记忆、智力、言语能力、抑制控制能力、视觉空间加工能力的差异是个体数学能力差异的基础；还有观点认为，数学能力的个体差别是由专门的数加工过程差异造成的，对此，研究者们关注的重点是数的表征．陈英和（2004）将算术认知分为简单与复杂两种，讨论了工作记忆的3个成分与两种算术认知的关系[5]，研究证明了中央执行系统对两种算术认知的作用，而语音环路对简单算术认知的影响仍有分歧，对复杂算术认知起重要作用，视觉空间模板对两种算术认知的作用尚不明确．吴赵敏等（2011）测试了儿童的基本数学能力各因素与视空间工作记忆的关系，发现数学运算和空间视觉能力均与视空间工作记忆呈相关．在数学学习中，较大的儿童比年幼的儿童能更多更好地利用语音短时记忆来保持数学问题信息[6]．有研究发现复述是影响儿童语音环路表现的重要因素，数学的加减法计算经常要用到复述的技巧来进位和退位，可见语音环路和数学成绩息息相关[7]．数学又需要用到大量的视觉和空间信息储存、判断功能，做数学题时需要用视觉模板引导眼睛移动将运算过程编码入工作记忆，另外空间也需要空间代码．在儿童心理发展的过程中，视空间工作记忆在数学学习中的作用会有很大的变化，学龄前阶段儿童的算术心理模型主要是视空型，而非言语和抽象的，这时视空间工作记忆就起着重要作用，直到他们习得算术符号和言语表征为止[8]．到小学中年级，视空间模板在算术上的作用就很少了[9]．赵振国（2009）以学前儿童为被试发现，他们的数量估算能力与数数能力、视觉空间认知能力之间有显著正相关，且数量估算能力与视觉空间认知能力的相关程度要更高一些[10]．章雷钢（2007）通过实验研究了空间和言语工作记忆在大、小数量表征上的作用，结果发现小数表征由空间资源通路负责，不需要言语参与，而大数表征属于言语计数的过程，需要言语复述机制参与；并在此基础上提出了数量表征的双通路模型，个体要通过言语工作记忆通路处理客体数量刺激的特征信息，通过空间工作记忆通路处理其位置信息，整个数量表征过程分4个阶段：客体索引、言语计数、数字符号构建和数量提取[11]．综合以上研究结论可以看出，儿童的近似数量表征能力、工作记忆均与数学学习紧密相关，该研究则重点探讨工作记忆中的语音环路与近似数量表征能力及数学成绩的关系．

1 对象与方法

1.1 研究对象

研究选取的被试为山东省烟台市某小学四、六年级学生共96人，分别为50人和46人，被试平均年龄分别是10.22岁和12.52岁．所有被试视力或矫正视力正常，均为右利手．实验后有小礼品赠送．经过两大实验测试，剔除正确率低于60%的被试后，所剩被试分别为33人和30人．

1.2 研究工具

实验在学校机房进行，采用集体施测，近似数量表征系统敏锐度使用Panamath1.2.2施测[12]，工作记忆使用E-prime1.1施测，测试均在电脑上进行．

1.3 研究程序

近似数量表征测试采用点阵比较任务，如图1所示，要求被试在不数数的情况下，快速判断哪种颜色的点数量更多（如黄点多按Q键，蓝点多按P键），记录判断反应时和正确率；语音环路测试所用材料分为字母和数字，如图2所示，要求被试对出现过的字母和数字进行延迟匹配（如出现过按F键，未出现过按J键），记录匹配反应时和正确率；数学成绩以小学生最近的一次期末考试成绩为参照．分别对四六年级学生进行两大项目的施测，要求儿童依次完成各测试．

图1 点阵比较任务

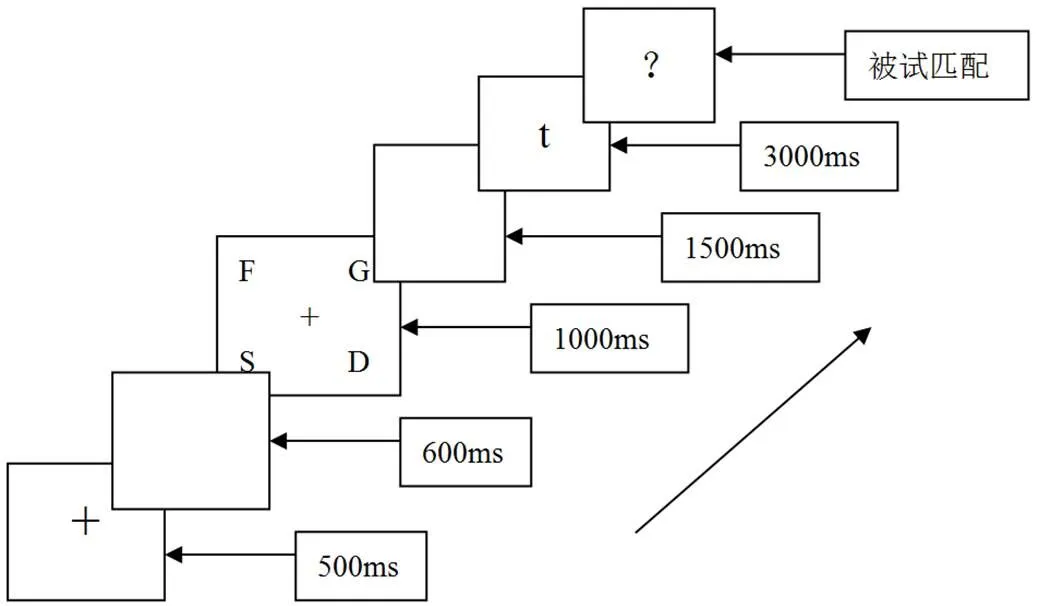
图2 语音环路测试任务（以字母为例）

1.4 统计方法

将各项测试结果输入表格中汇总整理，运用SPSS20.0对所得数据进行统计分析．

2 结果与分析

2.1 四年级和六年级学生各项成绩的描述性统计结果

小学生的注意力发展尚未完善，其注意转移和分散较为常见，因此暂不将反应时作为统计指标，只统计学生测试项目的正确率，具体结果如表1．

表1 四和六年级学生各项成绩的描述性统计结果（M±SD）

从表1可以看出，六年级学生各项测试的平均正确率都高于四年级的学生，其中，近似数量表征系统的差距最大，独立样本检验结果差异显著（=-2.938，=0.006）．随着儿童年龄和知识的增长，其认知水平、工作记忆能力等有所提升．

2.2 小学生近似数量表征系统和语音环路与数学期末成绩的关系

首先，将四、六年级学生的情况分开来看，结果如表2~表14所示．

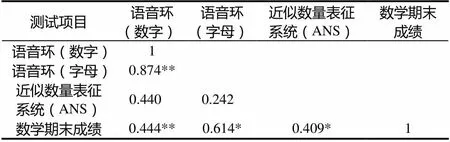
表2 四年级学生近似数量表征系统和语音环路与数学期末成绩的相关性

注：**<0.01，*<0.05，下同

从表2可以看出，四年级学生的近似数量表征能力、语音环路均与数学考试成绩有显著的正相关，近似数量表征能力与语音环路没有显著相关．

表3 四年级学生语音环路对数学成绩的回归分析

从表3可以看出，语音环数字成绩的标准化回归系数在0.01水平上边缘显著，语音环字母成绩的标准化回归系数在0.001水平上显著．以数学成绩为因变量，语音环数字成绩为自变量，可构建标准化回归方程=10.83+9.53，以语音环字母成绩为自变量建立的回归方程是=9.17+6.64．

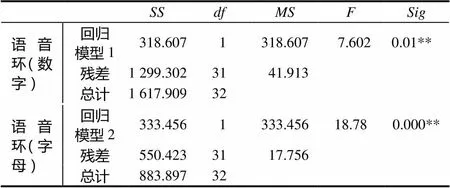
表4 四年级学生语音环路对数学成绩的回归模型的方差分析

从表4可以看出，回归模型1、2均显著（1=7.602，=0.01，2=18.78，=0.000），表明两个模型与数据的拟合程度很好．

表5 四年级学生ANS对数学成绩的回归分析

从表5可以看出，近似数量表征系统敏锐度的标准化回归系数在0.05水平上显著，以数学期末成绩为因变量，近似数量表征系统敏锐度为自变量，建立的回归方程是=0.106+9.25．

表6 四年级学生ANS对数学成绩的回归模型的方差分析

从表6可以看出，回归模型3显著（=6.211，=0.018），表明模型3与数据的拟合程度较好．

由上述可知，四年级学生的语音环路对数学成绩的回归显著，说明对他们的数学成绩有一定的预测作用．作为数学能力之一的近似数量表征能力（ANS）对学生的数学成绩也有很大影响，回归模型3说明近似数量表征能力对数学成绩回归显著且有预测作用．

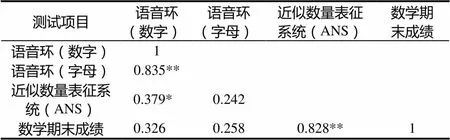
表7 六年级学生近似数量表征系统和语音环路与数学期末成绩的相关性

从表7可以看出，六年级学生的近似数量表征能力与数学考试成绩显著相关，并与语音环路的数字测试显著相关，语音环路与数学成绩无显著相关．在近似数量系统敏锐度与数学成绩的相关性上可以看出，六年级学生比四年级学生的相关程度更大，他们与数学接触的时间也更长．

表8 六年级学生ANS对数学成绩的回归分析

从表8可以看出，近似数量表征系统敏锐度的标准化回归系数在0.001水平上显著，以数学期末成绩为因变量，近似数量表征系统敏锐度为自变量，建立的回归方程是=0.133+12.74．

表9 六年级学生ANS对数学成绩的回归模型的方差分析

从表9可以看出，回归模型4显著（=61.002，=0.000），表明模型4与数据的拟合程度很好，说明近似数量表征能力对六年级学生的数学成绩有一定的预测作用．

表10 六年级学生语音环（数字）对ANS的回归分析

从表10可以看出，语音环（数字）成绩的标准化回归系数在0.001水平上显著，以数学期末成绩为因变量，语音环（数字）成绩为自变量，建立的回归方程是=15.496+11.99．

表11 六年级学生语音环（数字）对ANS的回归模型的方差分析

从表11可以看出，回归模型5显著（=4.704，=0.039），表明模型4与数据的拟合程度较好，说明语音环（数字）测试对六年级学生的数学成绩有一定的预测作用．而语音环字母测试与数学成绩、近似数量表征能力均无显著相关，这可能与六年级学生的言语复述能力更强有关，他们在工作记忆的语音环路测试中所用的复述资源比四年级学生少，且能将数字与字母区别对待；也和各项目的施测顺序有很大关系，这些方面还需要加以改进．

从整体上看两年级学生的情况，将数学期末成绩转化为标准分数，结果如下．

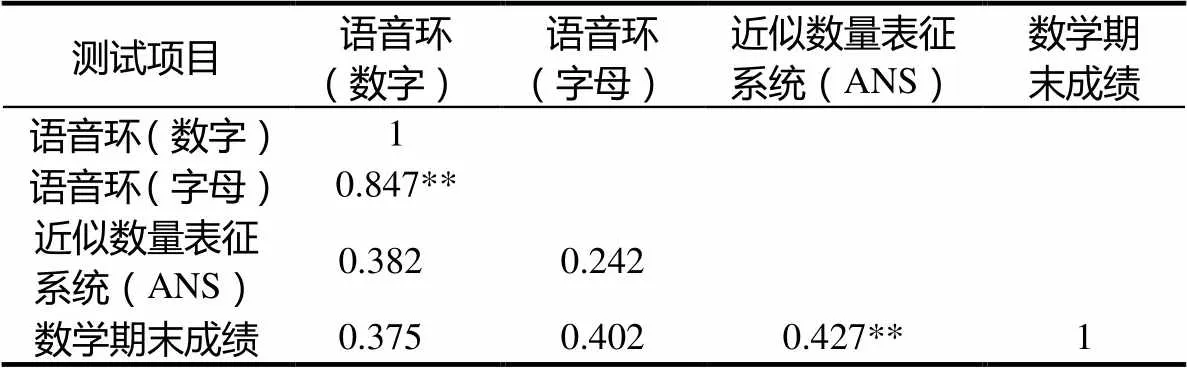
表12 两年级学生近似数量表征系统和语音环路与数学期末成绩的相关性

从表12可以看出，两年级学生的近似数量表征能力与数学考试成绩显著相关．

表13 两年级学生ANS对数学成绩的回归分析结果

从表13可以看出，近似数量表征系统敏锐度的标准化回归系数在0.01水平上显著，以数学期末成绩为因变量，近似数量表征系统敏锐度为自变量，建立的回归方程是=0.037+0.013．

表14 两年级学生ANS对数学成绩的回归模型的方差分析

从表14可以看出，回归模型6显著（=8.452，=0.006），表明模型6与数据的拟合程度很好，说明近似数量表征能力对两个年级学生的数学成绩均有一定的预测作用．

3 讨 论

由上述实验可以得出，小学生的近似数量表征能力与数学成绩息息相关，从不同年级学生的语音环路测试成绩与二者的关系来看，工作记忆同近似数量表征能力及数学成绩也有一定程度的关系．

儿童的近似数量表征系统敏锐度与年龄有关，马俊巍（2012）对小学二至五年级学生进行近似数量表征研究发现，五年级成绩要比二三四年级的成绩更好，其原因有两个方面：一是随着小学生年龄增长，近似数量系统逐渐成熟，因此敏锐度会越来越好；二是学校教育对近似数量系统敏锐度有很大影响[13]．Pica等人（2004）用接触过数学教育的法国成人和缺少数学经验的亚马逊土著居民为被试，发现前者的数量区分能力显著优于后者，表明除了自身的成熟发展外，数学学习经验对近似数量表征能力有重要影响[14]．工作记忆中的语音环路需要言语复述的参与，其任务难度和资源损耗都要高于近似数量表征系统，因此年级差异低于近似数量表征系统．关于数学能力的性别差异众多研究的结论并不一致，且这与样本量有很大关系，由于研究的样本量不够大，所以暂不讨论性别差异．

数学考试成绩反映出学生的数学认知情况，算术认知是数学考试的重要部分，陈英和（2004）的研究讨论了工作记忆三成分与算术认知的关系，研究证明了中央执行系统对算术认知有重要作用，语音环路对复杂的算术认知有显著影响，而对简单算术认知的作用研究者仍有分歧，视空间模板的作用尚未证实[5]．该研究部分地验证了以往研究的结论，数学的加减法计算经常要用到复述的技巧来进位和退位，可见语音环路和数学成绩息息相关．Inglis（2011）等人研究了儿童和成人近似数量系统敏锐度与数学能力的关系，发现只有儿童得到了显著正相关，而成人却不存在显著的相关关系[15]，这说明近似数量表征系统对数学能力的影响并非一直存在，它会随着年龄、知识经验的增长发生变化．Halberda等人（2012）的研究结果也说明了不同年龄段被试的近似数量表征系统敏锐度的差异明显，同一年龄段的不同个体间也有较大差异，它表明近似数量系统敏锐度有可塑性，而数学教育起到了很大的帮助作用[16]．

4 结论及启示

关于数学认知的研究有两种解释途径：一般的观点认为，个体非数字的认知能力如工作记忆、长时记忆、智力、言语能力、抑制控制能力、视觉空间加工能力的差异是个体数学能力差异的基础；还有观点认为，数学能力的个体差别是由专门的数加工过程差异造成的，对此，研究者们关注的重点是数的表征．小学生的近似数量表征能力与数学成绩关系密切，当然由于知识经验和自身成熟的不同，其密切程度不尽相同．这为现代的儿童数学教育提供了一个视角：能否通过训练儿童的近似数量系统敏锐度和数量表征能力来带动其提高数学学习兴趣与成绩呢？该研究分别对四六年级学生的近似数量表征系统测试和期末成绩进行了相关研究，其回归模型表明了二者间密不可分的关联，这说明增强儿童近似数量表征系统敏锐度可以在一定程度上提升其数学学习成绩．

然而，影响儿童数学成绩的因素有很多，工作记忆就是其中之一，甚至可以说它是数学成就的重要指标．在小学阶段，言语复述是儿童记忆的重要方法之一，数学学习个体差异的部分原因在于语音短时记忆，有研究表明，在数学学习中，较大的儿童比年幼的儿童能更多更好地利用语音短时记忆来保持数学问题信息[17]．Hutton和Towse（2001）报告说数字广度和数学成绩之间的相关是0.45，LeBlanc和Weber-Russell（1996）发现工作记忆变量可以解释儿童数学文字题解决中57%的变异[7]，Swanson和Beebe- Frankenberger（2004）的研究发现工作记忆与数学问题解决之间有0.54的相关度[18]．据此推测，通过训练，提高工作记忆能力可以促进儿童的数学学习进步，改善相关学科的学习，提高儿童问题解决效率的能力．该研究也部分证实了前人的发现，但因各方面条件所限，并未完全得出与前人研究一致的结论．

总之，小学生的数学能力是一个有多种心智技能复杂结合的有机整体，对小学生数学能力的培养是一个系统的逐步完善的过程，在不同的发展阶段要相应地采取不同措施，增进各种认知成分的训练，更要遵循学生的年龄特点，这些仍需要教学实践的检验．

[1] 王翠艳，刘广兵．儿童数量表征的发展与数学学习的关系及其干预[J]．心理探索，2013，（7）：40-43．

[2] Brysbaert M. Number Recognition in Different Formats [A]. In: Campbell J I D.[C]. Psychology Press: New York, 2004.

[3] 陈英和，赖颖慧．儿童非符号数量表征的特点及作用探析[J]．北京师范大学学报（社会科学版），2013，（1）：33-41．

[4] 王乃弋，罗跃嘉，李红．两种数量表征系统[J]．心理科学进展，2006，（4）：610-617．

[5] 陈英和．工作记忆与算术认知的研究现状与前瞻[J]．北京师范大学学报（社会科学版），2004，（1）：40-44．

[6] Holmes J, Adams J W. Working Memory and Children’s Mathematical Skills: Implications for Mathematical Development and Mathematics Curricula [J]., 2006, (26): 339-366.

[7] 姚颖蕾．小学生工作记忆的发展及其在数学学习中的作用[D]．华东师范大学，2011．

[8] Cantor J, Engle R W, Hamilton G. Short-Term Memory, Working Memory, and Verbal Abilities: How Do They Relate [J]., 1991, (15): 229-246.

[9] Imbo L, Vandierendonck A, Vergauwe E. The Role of Working Memory in Carrying and Borrowing [J]., 2007, (71): 467-483.

[10] 赵振国．3—6岁儿童数量估算、数数能力及视觉空间认知能力发展关系的研究[D]．华东师范大学，2009．

[11] 章雷钢．大、小数量表征的心理机制[D]．浙江大学，2007．

[12]  http://www.panamath.org/ 2015-11-10[Z].

[13] 马俊巍．学龄儿童近似数量表征的研究[D]．东北师范大学，2012．

[14]  Pica P, Lemer C, Izard V, et al. Exact and Approximate Arithmetic in an Amazonian Indigene Group [J]., 2004, 306(5 695): 499–503.

[15] Inglis M, Attridge N, Batchelor S, et al. Non-Verbal Number Acuity Correlates with Symbolic Mathematics Achievement: But Only in Children [J]., 2011, 18(6): 1 222-1 229.

[16] Halberda J, Ly R, Wilmer J B, et al. Number Sense Across the Lifespan as Revealed by a Massive Internet-Based Sample [J]., 2012, 109(28): 11 116-11 120.

[17] Holmes J, Adams J W. Working Memory and Children’s Mathematical Skills: Implications for Mathematical Development and Mathematics Curricula [J]., 2006, (26): 339-366.

[18] Swanson H L, Beebe-Frankenberger M. The Relationship between Working Memory and Mathematical Problem Solving in Children at Risk and not at Risk for Math Disabilities [J]., 2004, 96(3): 471-491.

[责任编校：周学智]

Relationship between Approximate Number Representation System, Working Memory and Mathematics Achievement of Primary School Students

KONG Hai-yan1, SUN Yu2, SONG Guang-wen3

(1. Academy of Education Science, Ludong University, Shandong Yantai 264025, China;2. Faculty of Education, Qufu Normal University, Shandong Qufu 273165, China;3. Institute of Psychological Assessment and Applied Psychology, South China University of Technology, Guangdong Guangzhou 516041, China)

Mathematical learning process required the participation of many cognitive activities. The study tested the primary school students’ ability of approximate number representation, working memory to explore the relationship between them and mathematics achievement. Results showed that pupils’ approximate number representation ability and working memory capacity had certain plasticity, they had a significant role in promoting math scores and increased with the age. School mathematical education worked vitally in this process. Approximate number representation ability and working memory could predict pupils’ math achievement in different degrees.

pupils; approximate number representation system; working memory

G622.0

A

1004–9894（2017）02–0014–05

2016–12–02

孔海燕（1979—），女，山东曲阜人，博士，主要从事青少年心理辅导、问题青少年的预防与教育研究．