用ISM法确定系列教科书的教学序列——以人教A版高中数学必修系列教科书为例

原玉娟，徐章韬



用ISM法确定系列教科书的教学序列——以人教A版高中数学必修系列教科书为例

原玉娟1，徐章韬2

（1．河南郑州龙湖一中，河南郑州 450100；2．华中师范大学数学与统计学学院，湖北武汉 430079）

用解释结构模型方法分析人教A版高中数学必修系列5册教科书，给出教科书的教学序列安排，为教师选择合理的教学顺序提供参考建议．在进行教材研究时，注意研究方法的创新是值得关注的问题之一．

ISM法；教科书分析；教学序列

1 引 言

教材分析研究是课程研究的重要主题之一．已有不少研究者从不同角度对此主题展开了研究．如，有研究者认为，问题变式是中国数学教材中问题设计的重要特色[1]；有的研究对高中数学教材中数学史的应用现状进行了分析[2]；还有的研究从HPM的角度对教材的编写作了对比研究[3]；还有的研究独辟蹊径，从封面设计的角度对小学数学教材的编写特色进行了分析[4]；还有的研究以某一课程内容为主题，建立课程难度、广度、深度的定量模型，展开量化研究[5~8]；近年来更多的是一些教材的国际比较研究，如，有的研究从教材整体知识结构的角度对中国和新加坡的教材进行了对比研究[9]，等等．上述研究从多种角度对教材进行深入的分析研究，给教材研究提供了宝贵的借鉴．教材研究的方式还在不断发展之中．还有一些研究把图论的方法用于教材分析之中，针对教材某一章节的内容进行了一些新尝试[10~12]．这种方法把量的分析、经验分析融为一体，在方法意义具有一定的参考性．

《普通高中数学课程标准（实验）》的必修系列课程包含了5个模块，人民教育出版社根据上述课程标准研制了相应的教科书《普通高中课程标准实验教科书·数学》，包括A、B两套教科书，这里以人教A版为例．这一系列教科书，共5册，分别是必修1、必修2、必修3、必修4和必修5．数学有其内在严密逻辑性，不是按模块化的方式组织的，但课程标准下的教科书却是按模块化的方式研制的，这就给教师确定教科书的教学序列带来了困惑．有些学校并不是按上述序列安排课程教学，而是选择了必修1、必修4、必修5、必修2、必修3这样的教学序列，也有些教师根据自己的经验体会提出了不同的教学序列安排[13]．据不完全统计，目前为止，河南省（郑州、南阳）、山东省、江西省（宜春）、河北省、广东省（中山）、辽宁省按照必修12345的顺序进行教学；深圳市按照必修12435的顺序进行教学；重庆市、贵州（遵义）、天津市、江西省按照必修14532的顺序进行教学；北京市、福建省、四川省、湖北省按照必修14523的顺序进行教学，另外，浙江（台州）按照必修1452的顺序教学（必修三不学）；厦门市按照必修13245的顺序进行教学；山西省按照必修13452的顺序进行教学.

课程标准只规定了必修、选修的内容和要求，没有规定教材教学系列的安排，那么，对系列教科书，究竟该选择什么样的教学序列，使之既符合数学知识发展的逻辑顺序，又利于学生的心理发展呢？这里采用科学的、定量的手段来回答这个问题．

2 研究设计

2.1 研究方法

解释结构模型方法[14]（Interpretive Structural Modeling Method, ISM）是将图论用于研究社会系统，研究其中复杂要素间关联结构的一种分析方法．该方法用于教学系统分析具有很好的效果．教科书是一种复杂的定性系统，为了安排合理的教学序列，需要实现教科书的结构化和序列化．在教科书的分析中，该方法最大限度地纳入了人们的经验和主观认识，并将教科书的结构以易于理解的、可视化的图形呈现出来．

根据ISM法，分析教科书结构的基本流程如图1所示．

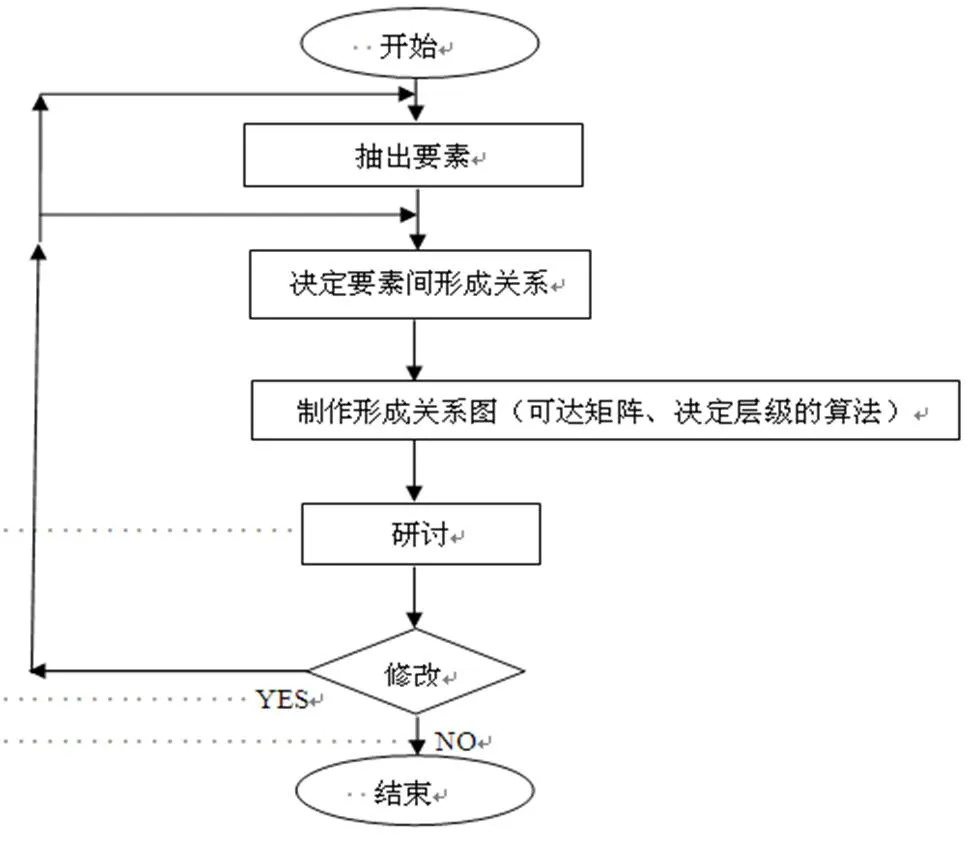
图1 根据ISM法分析教材结构的基本流程

2.2 研究过程

（1）抽出知识要素．

（2）确定各知识要素间的直接形成关系．

（3）制作形成关系图．

根据上面各要素之间直接关系的分析，可以制作形成关系图，如图2．

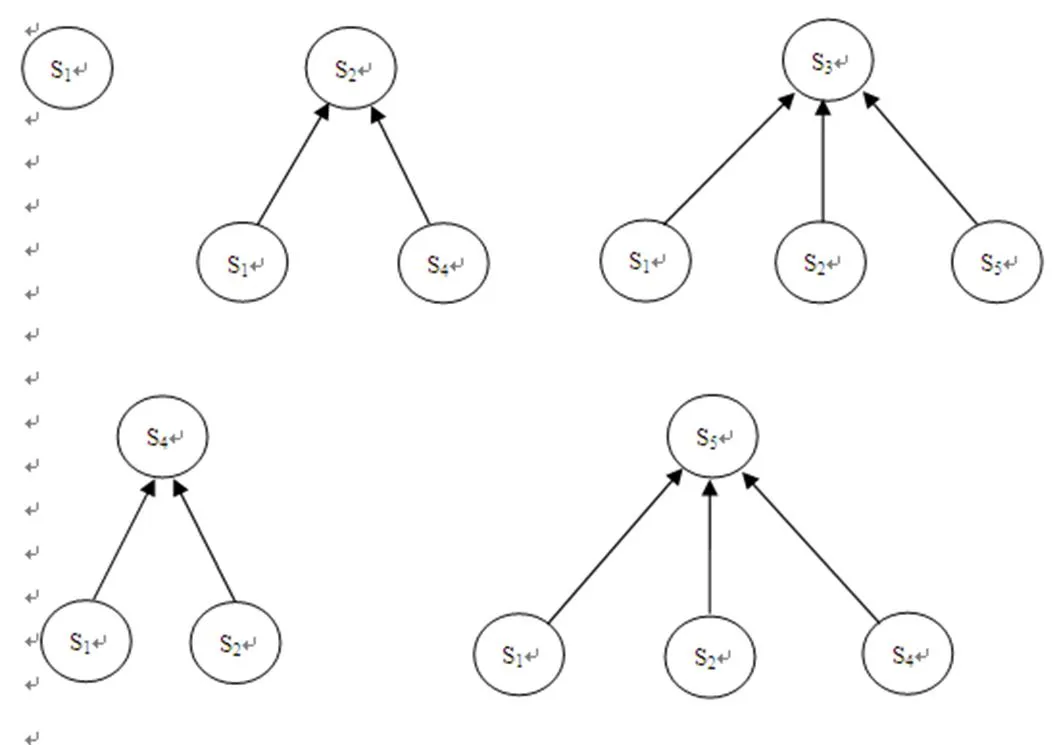
图2 要素间的关系图

对于上面的形成关系图，可以作出网状有向图，如图3．

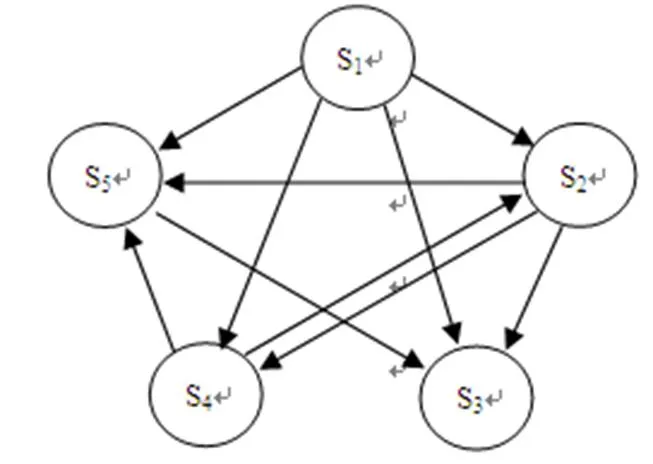
图3 要素间的有向图

（4）计算可达矩阵．

根据上面的网状有向图可以给出邻接矩阵．邻接矩阵是一个二值矩阵，矩阵中的每个元素只能是0或1．0表示该元素对应的两个顶点之间不存在边，1则表示该元素对应的两个顶点间存在边．表示单位矩阵．

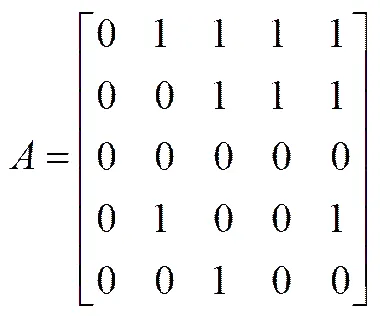
在邻接矩阵中，所表示的形成关系是一种直接形成关系，而可达矩阵中所表示的是一种间接的关系．标有“*”的元素1表示在()矩阵中，该元素为0．即在可达矩阵中，两要素之间是一种间接的关系．

（4）决定层级的算法．

(S)：从S出发，可能到达的全部要素的集合，称可达集合．

根据给出的可达矩阵，其中(S)、、如表1所示．

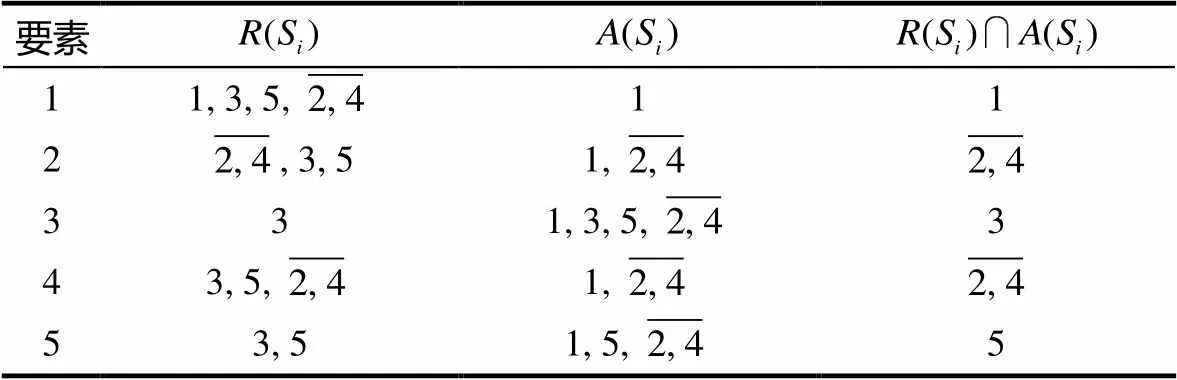
表1 可达矩阵中的要素

注：表中的表示2和4是强连接，表示这两个要素之间的关系相当紧密

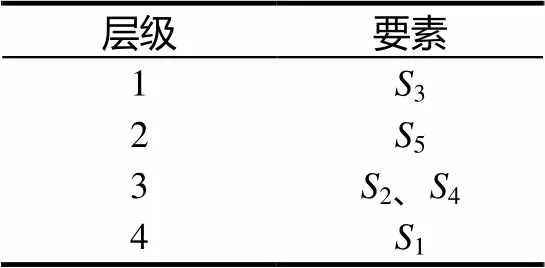
表2 要素的层级

2.3 研究结果

这样就形成了要素间的关系图，如图4．

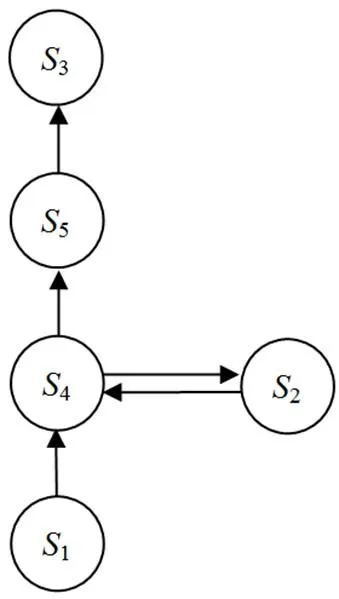
图4 要素间的关系

3 讨论与分析

根据ISM分析教科书序列得到的层次模型，应该先学习必修1，之后是处于并列地位的必修2、必修4，然后是必修5，最后是必修3，如表3．

表3 必修系列的教学序列安排方法

泰勒曾指出顺序性是课程内容的3个基本准则之一[15]．顺序性强调每一后继内容要以前面的内容为基础，同时又对有关内容加入深入广泛地展开．课程序列的安排要在逻辑顺序和心理顺序，直线式和螺旋式之间取得一定的平衡．采取什么样的教学序列，要受诸多因素的制约，不能仅仅考虑教学的方便，也不能仅仅考虑学起来简单，更不能想当然来安排，应综合考虑．如，章建跃编审认为，从内容顺序来看，可以考虑：工具性内容（如常用逻辑用语、向量、算法等）在前；确定性数学在前不确定性数学（统计、概率）在后；有限在前无限（导数、积分）在后；代数（函数）在前，解析几何、立体几何在后[16]．

3.1 从内容的角度看

必修1共有三章，112页；必修2共四章，144页；必修3共三章，145页，必修4共三章，147页，必修5共三章，103页．

必修系列课程内容按照4条主线展开．

（1）函数主线：集合、函数概念、基本初等函数Ⅰ（指数函数、对数函数、幂函数）、基本初等函数Ⅱ（三角函数、三角恒等变换、解三角形）、数列、不等式．

（2）几何主线：立体几何初步、解析几何初步、平面上的向量、直线方程、圆与方程．

（3）概率与统计主线：随机事件概率、古典概型、几何概型、随机抽样、样本估计总体、变量间的相关关系．

（4）算法主线：算法初步、算法与程序框图、基本算法语句、算法案例．

这4条主线：数及其运算、函数、空间观念、数形结合、统计、随机观念、算法等核心概念和基本思想是数学课程的“灵魂”，体现了寻求一般性模式的思想和追求简洁与形式完美的精神等，有助于学生领悟数学本质，体验数学中的理性精神，学会数学形式下的思考和推理训练．由于“模块化”与数学学科的内在结构之间有一定的矛盾，因此慎重地决定教科书的教学序列显得非常有意义．

高一上学期因必修1内容相对较少、在整个高中阶段难度相对较小，故需要从处于第二层级的必修2和必修4中再选一本继续学习．

从内容的主线来考虑：必修2中涉及到空间几何体，点、直线、平面之间的位置关系，直线与方程，圆与方程等几何主线的内容；必修4中有三角函数、平面向量、三角恒等变换三章内容．对于必修1来说，与之联系紧密的是必修4，因为其中涉及到了基本初等函数Ⅱ（三角函数，三角恒等变换），它属于函数主线里的内容．

从内容的多少来考虑：必修2共四章144页，必修4共三章147页．同时，在可达矩阵中，这两者之间的关系是强连接，两者在教学序列中的顺序孰先孰后，关系不大．因此，理论上讲，这两者对教学顺序的安排几乎没有什么影响．

从学生的接受能力、承受能力来考虑：必修2的内容虽比必修4的内容琐碎、但相对来说较容易些，对于高一学生来讲，由初中进入高中需要一个缓冲适应期，学习新知识要由易到难、循序渐进，二者比较，首选必修2．

综上所述，从内容的主线来考虑，高一上学期的教学序列应该为必修1（第一层级)、必修4（第二层级），高一下学期接着学习必修2（第二层级）、必修5（第三层级），高二上学期学习必修3（第四层级），即14253；从学生的接受能力、承受能力来考虑，高一上学期的教学序列应该为必修1（第一层级）、必修2（第二层级），高一下学期接着学习必修4（第二层级）、必修5（第三层级），高二上学期学习必修3（第四层级），即12453．

3.2 从教学经验的角度看

另外，从教学经验的角度分析，可以得出序列安排的一些原则：（1）代数内容不宜过于集中，不要“一竿子插到底”，要体现螺旋上升的特点；（2）几何内容不宜过于滞后，要及早发展学生的几何直观能力，用之于把“抽象的东西栖居在形象之上”，根据这个原则，也可以对比剖析一下其它的教学序列安排．

如果采用12543或者12453，这两种方法其实可以看作一类，展开线索是：函数——几何——函数——算法（中学教师不太熟悉的内容）、统计与概率．这种教学序列和以前人教社的混编教材的章节次序基本类同．有些地方采用的就是第二种方法．

如果采用14253或者14523，若从课程内容的内在连贯性去考虑，由于必修4与必修5的联系密切，有利于循序渐进地学习，14523应该是比较合理的顺序，因此第四种方法也被很多地区所采用．但这种次序把几何模块的位置放得太后，不利于及早培养学生的空间想象能力和几何直观能力．14253显然是看到了这一点，把几何模块放在必修4和必修5之间，虽有隔断两者之间联系的嫌疑，但也有可取之处，应把图形直观能力贯穿课程的始终，不能太滞后．

若采用15423，即是函数——几何——算法（中学教师不太熟悉的内容）、统计与概率，很明显，函数内容或代数内容过于集中，几何内容太滞后．

若采用列15243，其实和14253差不多，但还如第三种序列合理．

由此，教学序列12453，14253是比较合理的选择．其中12453序列和中国传统的教材序列其本类同，体现了传统经验的宝贵价值；但由于新课程无论在理念上，还是在内容的选择、编排上都有些变化，故选择14253也有其合理之处．教学序列的安排若能考虑到一线教师的教学经验，推动起来遇到的阻力必然会小得多，教师的经验也是必须考虑的重要因素之一．

3.3 从学习心理的角度看

中学生发展不仅与心理特征有关，而且还与生理特征有关，教科书序列的安排也要考．人有两种不同的思维方式或习惯，一种是语言——逻辑方式，一种是视觉——图形方式．有的中学生倾向于语言——逻辑方式，有的倾向于视觉——图形的思考方式，还有的中学生并不偏好哪一种方式，属“中间型”．生理学的研究也表明，左半脑长于语言、数值运算等方面的逻辑推理，右半脑在空间问题、想象力等方面起主导作用．根据心理学、生理学的研究，要统筹考虑代数、几何内容的教学序列．必修1、必修4和必修5研究的主要内容是代数，必修2的主要内容是几何，必修3是算法和概率统计等新增内容．按模块化的原则，必修1、4和5由于内在关联强，凝聚为一个大模块是合理的，但若按这种方式来安排教学序列的最大缺陷是几何课程出现得太晚．而20世纪八九十年代按分科课程授课时，空间立体几何在高一下学期就出现，因此，立体几何出现的时机不能太晚．那么几何课程应现在何时呢，结合前面的分析，按14253的顺序有其合理性．章建跃编审也指出[17]，按现行课程标准的顺序，高一（上）要学习函数的概念与性质、基本初等函数（Ⅰ）、立体几何、解析几何（直线与圆）等，学生的认知基础不够，难点过于集中，“螺旋上升”变成了“蜻蜓点水”，相隔一年后再学习圆锥曲线、空间向量与立体几何等，前面的知识已淡忘．必修5的三章内容关联性不强，相关内容可适当集中，可以按函数、立体几何、解析几何、统计与概率、微积分的顺序安排．高中数学教材结构主要应体现数学的内在逻辑性，不人为割裂相关知识．同时要兼顾学生的认知发展水平．例如，《解析几何》应在高二集中学习．

学习从属于发展，学习要有必要的重复和一定的螺旋度．根据随机进入教学理论的观点，要提高学习者的理解能力和知识迁移能力，需要对同一教学内容，在不同时间，不同情境下，为不同目的，用不同方式加以呈现的要求．可以有意识地将不同分支串联在一个知识系统，为学生提供从不同数学环境中看到同一现象的机会．代数、几何交替出现，使学生看到同一数学现象的多种表征，多试图沟通它们之间的内在关联，将有助于他们的理解，这也是课程的目标之一．

4 结 论

在进行教科书教学序列的安排时，只要4个模块不影响相关联系和知识储备，老师教学经验、价值观、思考方法、认知特点的不同，学校根据自己的情况安排教学内容，为教学的多样性提供空间，这也体现了“构建共同基础，提供发展平台”、“提供多样课程，适应多样选择”的新课程基本理念[13]．教育信息大多是一些量度水平较低的信息，对这些信息的处理较为困难，如何使教育研究走上科学的量化之路是值得研究的．经验筛选、数据挖掘、叙事分析相互平行、互补互证是重要的研究方法[18]．

数学是逻辑性比较强的学科，数学教材的逻辑性十分清楚，解释结构模型得到的教材要素层级有向图能够为教师备课优化教学设计，为学生自主学习提供理论帮助，为教师教育教学顺序提供了一个科学有效的方法，研究基于ISM方法、结合学习心理、教学经验做了一种尝试，给出了教科书的教学序列安排即必修12453，以期抛砖引玉．

[1] 孙旭花．问题变式：中国数学教材问题设计之特色[J]．数学教育学报，2012，21（3）：54-59．

[2] 张阳开．高中数学教材中数学史应用现状探析[J]．数学教育学报，2014，23（2）：95-98．

[3] 徐章韬，梅全雄．HPM视角下的数学教材编写[J]．数学教育学报，2009，18（3）：14-17．

[4] 张辉蓉，俞向军．小学数学教材封面设计的探索及思考[J]．数学教育学报，2014，23（3）：83-86．

[5] 孔凡哲，史宁中．四边形课程难度的定量分析[J]．数学教育学报，2006，15（1）：11-15．

[6] 张维忠，黄丽虹．新教材“三角形”课程难度的对比分析[J]．数学教育学报，2009，18（4）：61-64．

[7] 高文君，鲍建生．中美教材习题的数学认知水平比较[J]．数学教育学报，2009，18（4）：56-60．

[8] 徐章韬，梅全雄．信息技术在教科书中的编排[J]．电化教育研究，2013，（6）：80-85．

[9] 王奋平．中国和新加坡高中数学教材整体知识结构比较研究[J]．数学教育学报，2014，23（2）：14-18．

[10] 王晓丽，徐章韬．用ISM方法分析“函数及其表示”的内容结构[J]．中学数学，2013，（2）：63-64．

[11] 贺旭．用目标矩阵法分析和设计弧度制[J]．中学数学，2013，（10）：18-21．

[12] 郑金，徐章韬．基于ISM法分析人教版与北师大版教材——以“一次函数”内容为例[J]．中学数学教学参考，2013，（7）：6-8．

[13] 张俊，梅磊．关于高中数学新课程不同教学顺序的思考[J]．高中数学教与学，2012，（2）：4-7．

[14] 傅德荣，章慧敏．教育信息处理[M]．北京：北京师范大学出版社，2001．

[15] 施良方．课程理论——课程的基础、原理与问题[M]．北京：教育科学出版社，1996．

[16] 章建跃．当前中小学数学课程改革中的一些问题[EB/OL]．http://www.pep.com.cn/gzsx/jszx_1/jszj/gsjcbxry/zhangjy/ jcyj/201104/t20110408_1034024.htm

[17] 章建跃．大家都来关心高中数学课标的修订[J]．中小学数学，2014，（9）：66．

[18] 上海市青浦实验研究所．教师“行动教育”——青浦实验新世纪探索[J]．课程·教材•教法，2014，（3）：3-12．

[责任编校：周学智]

Determine Teaching-Learning Sequence of Series of Textbooks by ISM——Take PEP High School Mathematics Compulsory Series of Textbooks as Example

YUAN Yu-juan1, XU Zhang-tao2

(1. The No.1 High School of Longhu, Henan Zhengzhou 450100, China;2. Central China Normal University, Hubei Wuhan 430079, China)

Interpretive Structural Modeling Method was a method that used to study social system by Graph Theory’s method, which studied one of the methods between the complex elements of associative architecture analysis. The method was used for the analysis of teaching system had a very good effect. Taking ISM teaching material analysis method as the main research methods to analysis people’s education press compulsory series high school mathematics textbook five copies, then the textbooks could be serialized, thus the teachers could get suggestions from it to choose reasonable teaching order. In the textbook research, paying attention to the innovation of research method was one of the issues of concern.

ISM method; analysis of teaching material; teaching-learning sequence

G632

A

1004–9894（2017）02–0055–05

2017–01–20

湖北省高等学校省级教学研究项目——卓越数字化教师培养的路径和条件分析——以数学教师为例（2015095）；华中师范大学重大科研课题及创新示范基地培育项目——TPACK视角下卓越数字化教师的培养研究（CCNUE2015-05）

原玉娟（1986—），女，河南鹤壁人，硕士，主要从事中学数学教与学研究．徐章韬为本文通讯作者．