基于高频电压注入法的PMSM离线参数估计方法

王 超,朱鹏远,符晓玲

(昌吉学院,昌吉831100)

0 引 言

永磁同步电机(以下简称PMSM)[1]具有效率高、发热少、可靠性好等优点,在工业领域广泛应用。PMSM控制器中包含电流和速度控制器,其基于电机内部参数进行设计。为了实现精确控制,电机的内部参数(电阻和电感等)必须准确[2]。然而,在实际应用中,电机参数会随着环境的改变而改变,根据电机铭牌数据计算的参数与实际参数之间存在一定偏差[3]。为此,需要一个电机参数估计系统来获得不同电机个体的自身参数,以此来实现高精度和高效率的控制器[4]。

电机参数主要为定子电阻和定子电感[5]。定子电阻的估计通常采用伏安法,即给定子线圈注入一定幅值的电压,并检测稳态时反馈的电流来计算定子电阻[6]。定子电感的估计通常是基于电机的电阻与电感的串联模型,通过注入恒定电压并检测电流上升的时间常数,然后结合定子电阻即可计算出电感[7]。然而,该方法不能同时测量d轴和q轴电感。最近,出现了一种称为高频电压注入[8]的方法,给定子注入高频电压,根据稳态时的电流幅值来计d轴和q轴电感。然而,在电机转动下利用该方法进行参数估计的时间较长,且没有考虑电机铁损,致使估计精度不高。

为此,提出一种在电机静止状态下,基于高频电压注入法的PMSM离线参数估计方法,用来估计定子电阻和电感。基于伏安法来估计定子电阻,利用高频电压注入法和FFT算法来估计d轴和q轴的电感。实验结果表明,提出的方法能准确估计出电机参数,与实际值的误差不超过0.5%,具有较高的实用性。

1 提出方法的基本架构

1.1 PMSM建模

PMSM通常等效成一个转子旋转坐标系(d-q轴)电路[9],如图1所示。其中,d轴和q轴的定子电压表示:

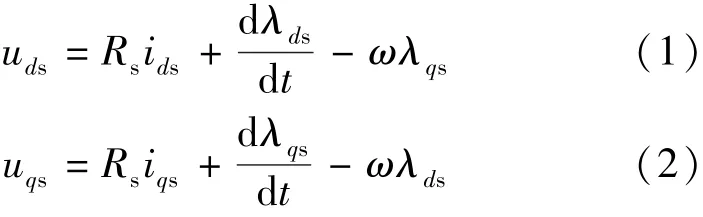
式中:uds和uqs分别为d轴和q轴的输入电压;ids和iqs分别为d轴和q轴的电流;Rs为定子电阻;ω为角速度;λqs和λds分别为d轴和q轴的磁链。

另外,由于提出的方法在静止状态下估计参数,所以d轴和q轴的反电动势为0,即:

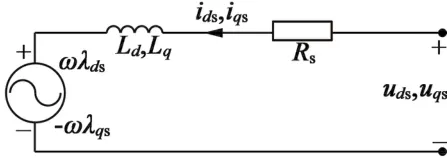
图1 PMSM的等效电路

1.2 提出的参数估计方法架构

提出的参数估计方法框架如图2所示,主要分为两部分,即定子电阻估计和d,q轴电感估计。其中,定子电阻估计过程较为简单,分别利用d轴或q轴的电压和电流来计算定子电阻。

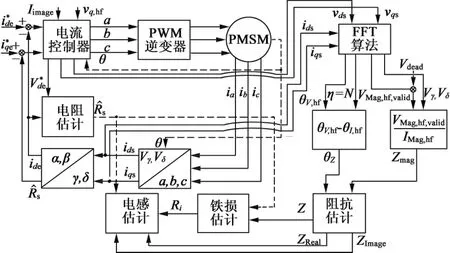
图2 提出的参数估计方法的总框图

对于d轴和q轴电感的估计,采用了高频电压注入法。其基本思想:分别在d,q轴注入带直流偏置的高频交流电压信号,并传递到电机中。然后,采集电机反馈的d,q轴的电流,并利用FFT对电压信号和反馈电流信号进行频谱分析,提取其基波信号。接着,通过基波电压和基波电流的幅值、相位关系来估计总阻抗。最后,基于总阻抗、铁损电阻和所估计的d,q轴电阻,来估计d,q轴的电感。

2 基于伏安法的电阻估计

本文根据伏安法,即电流控制器输出电压除以d轴或q轴反馈的电流来估计定子电阻,其中电流控制器根据从编码器获得的转子位置信息来控制电流。定子电阻估计的表达式:

在动态估计中,由于绝缘栅双极晶体管(IGBT)的非线性电压特性,会导致估计值产生偏差[10]。然而,本文方法是在电机静止状态下进行估计,所以不存在上述误差。另外,由于d轴电流是在磁链产生方向上的无功分量,所以不产生速度。那么,d轴参考电流使用接近额定电流的值,而q轴参考电流使用接近零的值。

3 基于高频电压注入法的电感估计

3.1 磁链和电感之间的关系

在提出的基于高频电压注入法的电感估计方法中,转子磁极方向的磁路非线性饱和影响电感的估计[11]。另外,本文在电感估计中考虑了铁损因数,因此需要分析在存在铁损下磁链和电感之间的关系。

PMSM的磁链由定子磁链和永磁体磁链给定,其表达式:

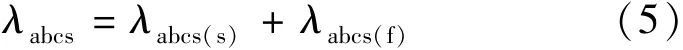
式中:λabcs(s)为定子绕组的漏磁链;λabcs(f)为永磁体的漏磁链。另外,电机的三相磁链可以转换为d,q轴磁链来表示,即:

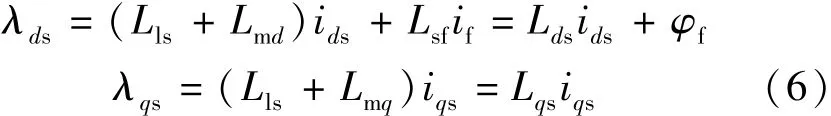
式中:Lls为漏感;Lm为d,q轴的磁化电感;Lsf为基于转子位置的永磁体电感。

图3为在考虑铁损下的d轴电感等效电路。其中,idi为铁损电流,Ri为铁损电阻,idm为d轴磁化电流。

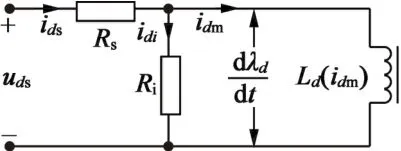
图3 d轴电感的等效电路

那么,磁链与电流之间的特性曲线可以分离为区域I和II,如图4所示。区域I为磁化部分,其斜率表示线性电感。区域II为渗漏部分,P为磁化饱和点。区域II中的电感由于饱和状态而具有较小的值。

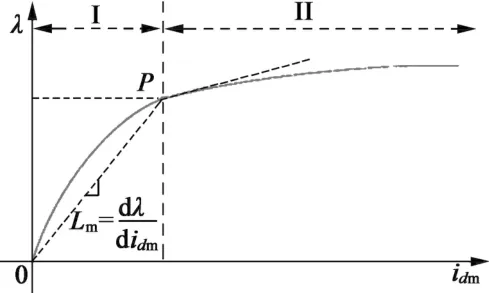
图4 磁链与电流的特性图

式(7)和式(8)分别表示在饱和状态和线性状态时由磁化电流所产生的磁链[12]:

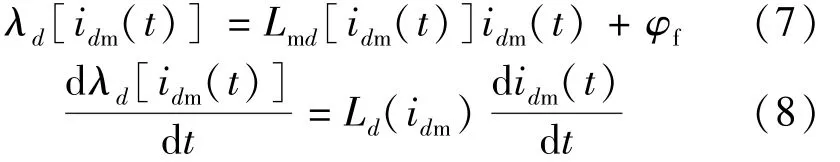
式(8)可以重新写成:

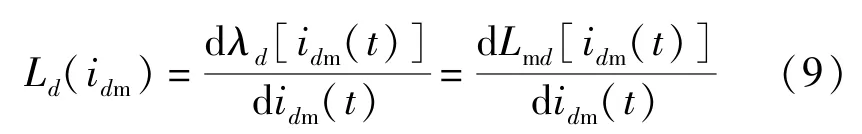
因此,由磁化电流产生的d轴电感可表示:

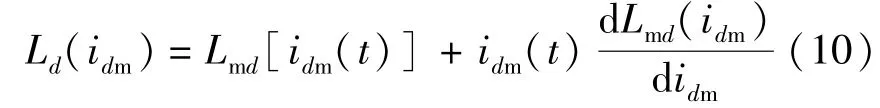
3.2 电感估计

本方法中,参数是在静止状态下估计,高频电压分量由是外部注入的,因此d,q轴的电压和电流中包含该高频分量。该高频信号的电压Vhf表示:

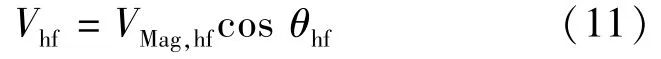
式中:θhf为相位;VMag,hf为幅值。

为了估计d,q轴电感,需要采集包含高频分量的电流(Ids,Iqs)和电压(Vds,Vqs),并通过FFT提取出信号的实部和虚部分量。基于获得的实部和虚部分量,d,q轴电压和电流信号的幅值(IMag,hi,VMag,hf)和相位(θI,hf,θV,hf)可表示:

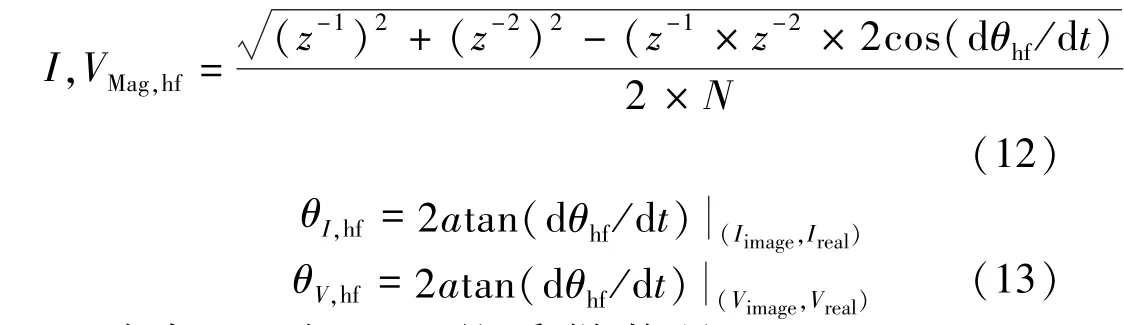
式中:N为 FFT的采样数量;tan(dθhf/dt)=

此外,式(12)中幅值没有死区时间补偿[13]。因此,有效电压(Vmag,hf,valid)应定义:

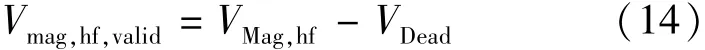
VDead为死区时间的补偿电压,定义:

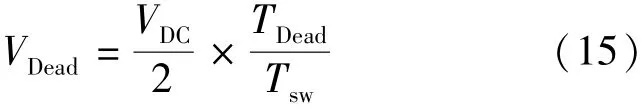
式中:VDC为直流母线电压;Tsw为开关周期;TDead为死区时间,设置为 2 μs。

总阻抗Z可以根据电压与电流的幅值和相位来计算获得。根据阻抗向量表示法,总阻抗Z可分为电阻ZR和电感ZωL,如图5所示。因此,总阻抗的幅度ZMag和相位θZ定义:

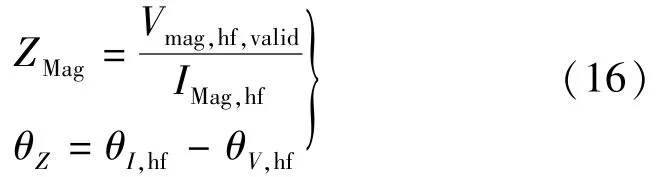
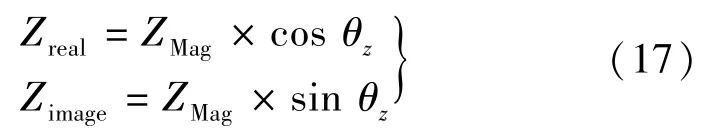
基于总阻抗的实部、虚部和上节估计的电阻,则铁损电阻Ri表示如下:

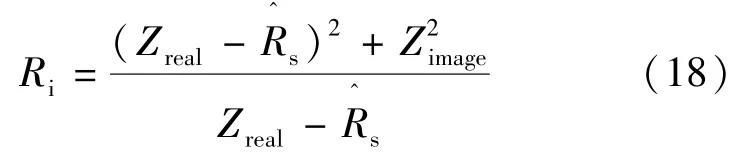
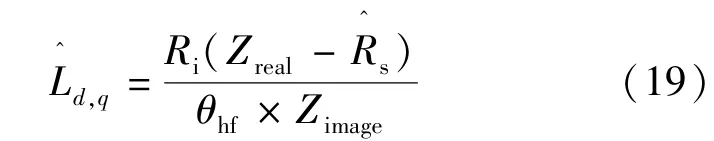
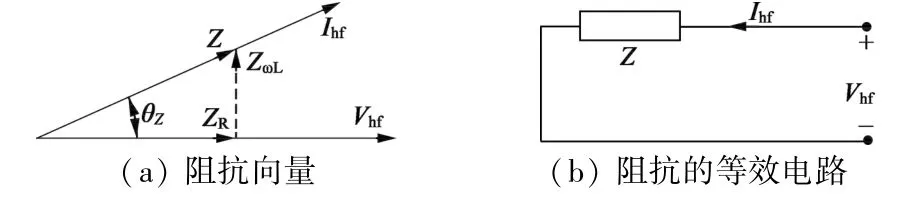
图5 总阻抗

4 实验及分析

4.1 实验设备

图6为实验设备,由三电平逆变器和控制板组成电路控制部分,将一个永磁同步发电机(PMSG)与PMSM级联作为负载。表1列出了电机参数。对于加入的高频电压信号,设定其频率fhf为1 kHz,幅值Vd,qhf为15 V。另外,在电感估计中,设置FFT的采样数N为128。

在电阻估计时,d轴参考电流接近额定电流值;而在电感估计时,其运用高频参考电压,所以d,q轴参考电流接近于零。

图6 实验设备

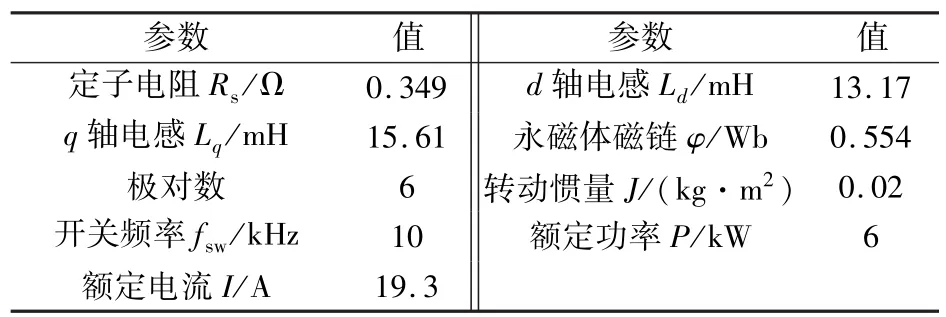
表1 电机参数

4.2 实验结果

在本文的方法中,通过注入高频电压信号来估计电机参数。图7显示了从d轴和q轴中检测出的高频电压信号波形。

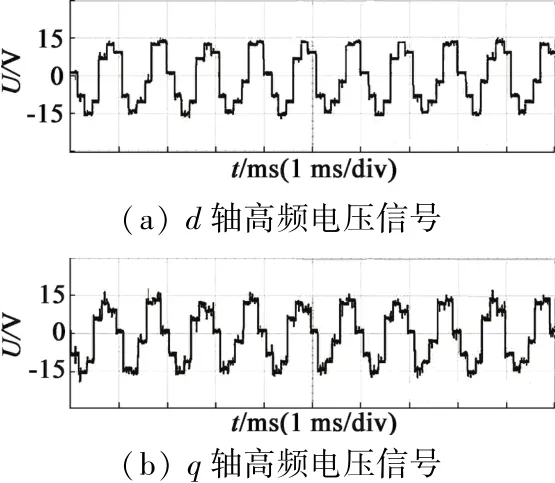
图7 d轴和q轴的高频电压信号

首先进行定子电阻估计。估计的电阻值也将用于电感估计,因此电阻估计必须准确。图8显示了定子电阻估计曲线,其中初始值设为0。可以看出,估计电阻值大约0.352 Ω,与实际值仅偏差0.86%。

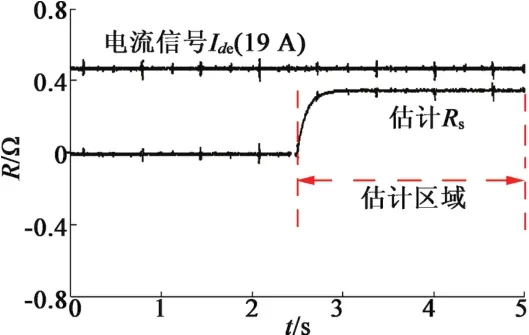
图8 定子电阻的估计结果

图9显示了在开关频率为10 kHz,d轴和q轴电感初始值设为0时的电感估计结果。可以看出,d轴电感的估计值约为13.21 mH,与实际值偏差仅为0.304%。q轴电感的估计值约为15.54 mH,与实际值偏差仅为0.448%。证明了所提出的方法能够精确地估计电感值,具有可行性。

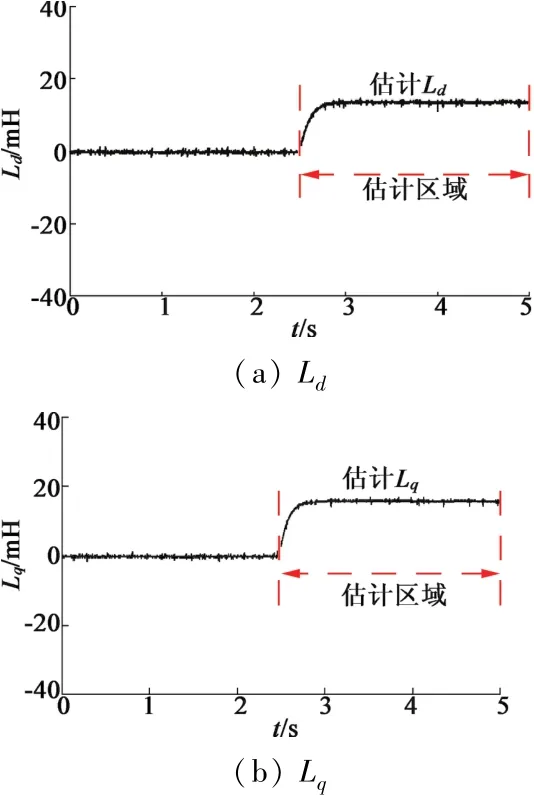
图9 初始值为0时的电感估计结果

为了验证初始设定值对估计结果的影响,设定d轴和q轴电感初始值比实际值高出50%,即d轴电感为19.75 mH,q轴电感为23.41 mH,估计结果如图10所示。可以看出,估计结果与初始值设为0时的结果基本一致,这证明了提出的估计方法性能与初始值无关。

图10 初始值较高时的电感估计结果

5 结 语

为了解决PMSM参数的离线估计,提出了一种基于高频电压注入法的电机静态离线参数估计方法。通过在电机模型中的d,q轴上注入高频交流电压信号,并采集电机反馈电流来计算定子电阻。通过对d轴和q轴电压和电流信号进行分析来估计定子电感。实验结果表明,提出的方法能够精确估计出电机参数,与实际值偏差不到0.5%,且不受初始值的影响。

[1] 李红梅,陈涛.永磁同步电机参数辨识研究综述[J].电子测量与仪器学报,2015,29(5):638-647.

[2] 林辉,吕帅帅.基于双 STF-UKF算法的永磁同步电机参数联合估计[J].东南大学学报自然科学版,2016,46(1):49-54.

[3] LI H,ZHANG H,YI X.The implementation of parameter identification in the control of permanent magnet synchronous motor[C]//2011 2nd International Conference on Artificial Intelligence,Management Science and Electronic Commerce(AIMSEC),IEEE,2011:2562-2566.

[4] LIN H,HWANG K Y,KWON B I.An improved flux observer for sensorless permanent magnet synchronous motor drives with parameter identification[J].Journal of Electrical Engineering&Technology,2013,8(3):516-523.

[5] 马建伟,梁晓琳,张鹏飞.混合动力汽车用内置永磁同步电动机参数估计方法研究[J].微特电机,2016,44(8):35-39.

[6] 王莉娜,杨宗军.SIMULINK中PMSM模型的改进及在参数辨识中的应用[J].电机与控制学报,2012,16(7):77-82.

[7] LIN H,HWANG K Y,KWON B I.An Improved Flux Observer for Sensorless Permanent Magnet Synchronous Motor Drives with Parameter Identification[J].Journal of Electrical Engineering&Technology,2013,8(3):516-523.

[8] 徐海珠,谢顺依,王鼎,等.基于旋转高频电压注入的对转PMSM无传感器控制[J].微特电机,2012,40(3):51-53.

[9] 刘侃.永磁同步电机多参数在线辨识研究[D].长沙:湖南大学,2011:18-19.

[10] 陈斌,王婷,吕征宇,等.电压型逆变器非线性的分析及补偿[J].电工技术学报,2014,29(6):24-30.

[11] MEDIMADJ S,DIALLO D,MOSTEFAI M,et al.PMSM drive position estimation:contribution to the high-frequency injection voltage selection Issue[J].IEEE Transactions on Energy Conversion,2015,30(1):349-358.

[12] MOHAMMED O,KHAN A A,MOHAMMED A,et al.A wavelet filtering scheme for noise and vibration reduction in high-frequency signal injection-based sensorless control of PMSM at low speed[C]//IEEE Power&Energy Society General Meeting.2012:250-260.

[13] 周虎.永磁同步电机参数在线辨识算法研究[D].成都:电子科技大学,2012:52-64.