基于综合学习粒子群算法的PMSM滑模观测器设计
2017-05-04韩方阵李国勇胡春红
韩方阵,李国勇,胡春红
(1.太原理工大学,太原030600;2金堆城钼业集团有限公司,渭南712101)
0 引 言
近年来,永磁同步电机(以下简称PMSM)无速度传感器控制策略日益成为电机控制领域研究的一个热点。常用控制策略大致可分为以下几类:激励信号法和高频信号注入法[1],硬软件结合法[2]和卡尔曼滤波器衍生的各种方法[3-4]等。第一类主要是基于电机模型,实现降阶或全阶观测器的闭环操作,存在对电机参数精度要求过高的限制;第二类是利用电机自身固有属性来实现;最后两类主要都是通过硬软件相结合来提高预测精度,但这无疑增加了研究成本。滑模观测器以其较高的测量精度和优良的鲁棒性成为最具发展潜力的研究对象[5-11]。并由此推出诸如离散滑模观测器[5]、无速度传感器滑模观测器[6-7]以及改进滑模观测器[8-11]等。
尽管在以上文献中滑模观测器存在很多卓有成效的研究方法,但依然无法消除滑模观测器抖振所带来的不利影响。因此,采用粒子群算法对超螺旋滑模观测器优化,降低观测器对抖振干扰的敏感性降低,并利用锁相环对优化后的转子相位角进行锁相处理,使估测结果最大程度地趋近真实值。
1 PMSM的数学模型
对PMSM分析时,常因磁路饱和、空间磁场的分布呈非正弦以及磁滞和涡流等因素存在,难以对PMSM建立数学模型。故设电机工作在非饱和区,且忽略磁场分布、磁滞等带来的不利影响。因此,在两相静止的坐标系中,建立如下的PMSM模型:
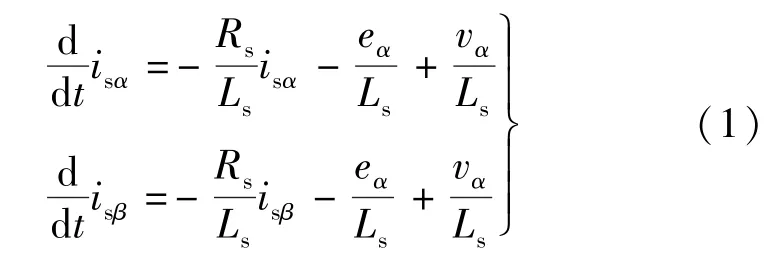
式中:Rs为定子电阻;Ls为定子电感;vα,isα分别为α轴上的电压和电流分量;vβ,isβ分别为β轴上的电压和电流分量;eα,eβ为静止两相反电动势。

式中:ωr为电机的电角速度;θr为电机的电角速度;ψf为永磁体与定子交链磁链。
2 ICLPSO优化的超螺旋观测器设计
本节引入改进综合学习粒子群算法(以下简称ICLPSO)[8]对超螺旋滑模观测器进行优化。ICLPSO优化超螺旋滑模观测器原理如图1所示。
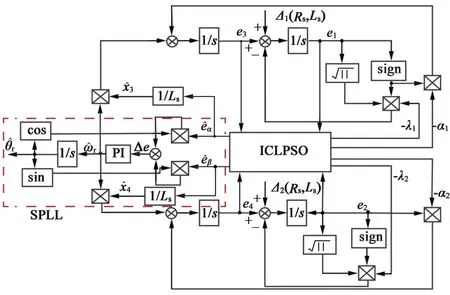
图1 ICLPSO优化超螺旋滑模观测器原理图
2.1 建立超螺旋滑模观测器
传统形式的超螺旋算法方程如下[10]:

式中:X1是实际变量值;是估计变量值;e1=X1-;X是算法的输出观测值。2
结合式(1)~式(3),设计基于超螺旋算法的观测器,在这里取 isα和 isβ为 x1和 x2,选 eα/Ls和 eβ/Ls为x3和x4。其中,带“^”号的为观测值。
因此,可以得到观测器的差动态方程:

式中:ei=xi-,i=1,2,3,4;Δ1(Rs,Ls)和 Δ2(Rs,Ls)为PMSM受到温升等引起的电阻参数变化及负载突变等影响产生的摄动不确定量。
分析误差动态方程式(5)可以得出,如果λ1,λ,α,α 取合适的值,可以保证误差项e,e,,21212,最终趋近于零,即:观测值(,)收敛到给定值(x3,x4)。
电角度可通过下式计算得出:
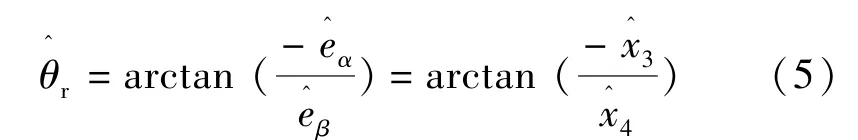
2.2 ICLPSO优化超螺旋观测器理论分析
由上节分析可以得知,利用滑模算法获得合适的λ1,λ2,α1,α2值,并分别用于矢量控制系统的速度调节和坐标变换,使得PMSM转子转速能够跟踪给定值。因此,可构造如下目标函数:


将式(5)代入式(8)可得:

又知e1e3为e1或e3的高阶无穷小,e2e4为e2或e4的高阶无穷小,故可忽略这两项。因此,可将式(9)改写为:

为求解式(10),引入ICLPSO算法,具体如下:
将e1,e2,e3,e4离散化,建立适应度函数:

式中:ω1,ω2,ω3,ω4为适应度函数的加权因子,代表适应度函数中4个分量的重要程度。
ICLPSO优化观测器的主要步骤[8,11]:
Step1通过坐标变换得出电机运行数据:vα,isα和 vβ,isβ;
Step2参数初始化。给定Rs,Ld,Lq与ψf等待辨识参数的取值范围,设定全部粒子的初始位置和速度,进化(迭代)代数初始化t=0,其最大值设为tmax;
Step3当i=1,2,…,N时,运行Step1~Step3;
1)更新权重。

式中,权重初值ωstart=0.9,权重终值ωend=0.4,k为迭代代数;
2)当fni≥m时,用基本PSO算法更新粒子速度、位置,fni=0;
当fni<m且i=1,2,…,N时,用式(12)更新粒子速度和位置:

Step4按式(13)计算第i个粒子的增长率gi:

Step5当gi<λ时,ci恒定,按式(14)对粒子运动方程加入高斯扰动进行更新调整:
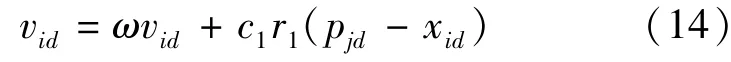
Step6当gi≥λ时,按式(15)更新ci:

Step7粒子种群迭代更新;
Step8更新迭代次数t=t+1。当t>tmax或末次迭代中gd的适应度小于设定阈值时(该阈值为PMSM待辨识参数的规定精度),输出gd=gd,终止迭代;否则,返回Step3。
利用所估计的角度值,用图1虚线框中的软件锁相环(SPLL)估计PMSM的转子角速度,为观测器观测的转子角位置。
3 仿真及结果分析
图2为永磁同步电机调速系统原理框图,结合图1及图2,通过MATLAB/Simulink对基于ICLPSO优化的观测器进行仿真。在零时刻,对PMSM模型施加一个如图5所示的梯形信号作为理想转速。图4~图6为分别对经ICLPSO优化前后滑模观测器测量的转子角磁通角、频率及电磁转矩进行仿真,并与传统滑模观测器对比。
调速系统采用id=0的矢量控制方案。永磁同步电机的具体参数:额定功率1.2 kW,额定电流5 A,额定电压380 V,给定转速100 r/min,定子电阻0.525 Ω,定子电感1.65 mH,磁链幅值0.074 4 Wb,极对数为4。ICLPSO参数初始化:迭代次数为maxgen=100,种群规模为sizepop=20,个体位置范围为[popmin,popmax]= [- 5,5],速度范围为 [Vmin,Vmax]=[- 1,1]。

图2 永磁同步电机调速系统框图

图3 ICLPSO最优个体适应度进化过程

图4 传统滑模观测器与ICLPSO转矩对比

图5 传统滑模观测器与ICLPSO转速对比

图6 传统滑模观测器与ICLPSO磁通角对比
结合仿真结果,可得出如下结论:
1)从图3可知,ICLPSO算法在第26代已经得到最优适应度值,收敛速度快,寻优效果好;
2)图4、图5表明,传统滑模观测器测量结果存在十分严重的抖振,跟踪效果差,经ICLPSO优化的滑模观测器跟踪效果明显优于传统观测器;
3)图6表明,传统滑模观测器配合软件锁相环在磁通角观测上与经ICLPSO优化的滑模观测器并无明显不足。
4 结 语
通过ICLPSO优化前后仿真的结果对比,可以验证ICLPSO算法优化的超螺旋滑模观测器控制的同步电机转速最大误差由30 rad/s锐降至0.95 rad/s,相应的轿厢每秒运行的最大位移偏差也由5.5 cm降至0.475 cm。同时,转子输出转矩抖振也明显减轻。因此,可以得出如下结论:
为克服传统的粒子群算法易于过早陷于局部收敛,在粒子迭代进化时引入增长率算子,对粒子运动速度进行动态调整,从而改进了综合学习粒子群算法的性能,提高了粒子全局搜索的能力,并且能有效克服过早陷入局部收敛,使螺旋滑模观测器较高精度的跟踪转子转速等关键信息。
[1] BETIN F,CAPOLINO G A,CASADEI D,et al.Trends in electrical machines control:Samples for classical,sensorless,and fault-tolerant techniques[J].Industrial Electronics Magazine,IEEE,2014,8(2):43-55.
[2] KUNG Y S,THANH N P,WANG M S.Design and simulation of a sensorless permanent magnet synchronous motor drive with microprocessor-based PI controller and dedicated hardware EKF estimator[J].Applied Mathematical Modelling,2015,39(19):5816-5827.
[3] KUNG Y S,HIEU N T.Simulink/Modelsim Co-simulation of EKF-based Sensorless PMSM drives[C]//2013 IEEE 10th InternationalConferenceon PowerElectronicsand Drive Systems(PEDS).IEEE,2013:709-713.
[4] KENDOUCI K,MAZARI B,BENHADRIA M R,et al.Speed-sensorless direct torque and flux control of PMSM based on extended Kalman filter using space vector modulation[C]//2015 3rd International Conference on Control,Engineering&Information Technology(CEIT),IEEE,2015:1-5.
[5] BERNARDES T,FOLETTO MONTAGNER V,GRUNDLING H A,et al.Discrete-time sliding mode observer for sensorless vector control of permanent magnet synchronous machine[J].IEEE Transactions on Industrial Electronics,2014,61(4):1679-1691.
[6] ALWI H,EDWARDS C.Second order sliding mode observers for the ADDSAFE actuator benchmark problem[J].Control Engineering Practice,2014,31(1):74-91.
[7] BARATIERI C L,PINHEIRO H.New variable gain super-twisting sliding mode observer for sensorless vector control of nonsinusoidal back-EMF PMSM[J].Control Engineering Practice,2016,52(7):59-69.
[8] 林国汉,章兢,刘朝华,等.改进综合学习粒子群算法的 PMSM参数辨识[J].电机与控制学报,2015,19(1):51-57.
[9] 李政,胡广大,崔家瑞,等.永磁同步电机调速系统的积分型滑模变结构控制[J].中国电机工程学报,2014,34(3):431-437.[10] 易伯瑜,康龙云,陶思念,等.永磁同步电机抗扰高阶滑模观测器设计[J].电工技术学报,2014,29(5):132-140.
[11] 张欣,李兵,姚明林.多种群遗传算法滑模观测器系统设计[J].微特电机,2016,44(1):48-50.
