多自由度纵弯复合模态球型超声波电动机研究
2017-05-04李兆胜赵学涛
李兆胜,赵学涛,刘 荣,陈 晨
(山东理工大学,淄博255049)
0 引 言
超声波电动机是近几十年发展起来的,一种利用通有交变电压的压电陶瓷来激发定子弹性体的固有频率振动在摩擦力的作用下使转子运动的新型驱动器[1]。超声波电动机具有结构简单、体积小、重量轻、惯性小、低速大转矩、响应快、断电自锁、不受电磁干扰等优点[2-3]。
在当前超声波电动机的研究中,虽然结构多样,但大部分输出形式单个自由度,较为单一[4-6],并且其机械输出性能(如力矩)也受到严重制约[7],难以满足空间机构和机器人关节等领域对于直接驱动的需求。本文基于对纵弯复合模态的研究,提出一种四换能器式悬臂梁超声波电动机,可实现转子球多自由度运动,由于每个自由度都由两个换能器进行驱动,故其输出力矩较大,适合在全方位仿真运动球形关节、机械手臂关节、机器人眼球等领域的应用。
1 电机的结构和原理
1.1 电机定子的结构

图1 电机驱动器结构图
本文主要对电机的驱动器进行设计,转子球根据电机驱动器尺寸参数进行选取,图1为所设计的超声波电动机驱动器结构图。该电机驱动器由两两对称的4个悬臂梁纵弯换能器和中间的圆筒构成。换能器对称分布,两端为端盖,螺柱连接其两端。在螺柱上固定着4片纵振陶瓷片和4片弯振陶瓷片。纵振陶瓷片中间设计有圆孔,与螺柱紧压在一起。弯振陶瓷片分为两半片的形式,根据所处位置的不同分为上下半片和左右半片,从而可以实现弯振。相邻近的陶瓷片彼此粘接在一起,与悬臂相邻的陶瓷片也与悬臂粘接,悬臂和圆筒为一体。电极片贴在陶瓷片沿厚度方向的横截面上,因电极片非常薄,设计时厚度可忽略不计。
1.2 电机工作原理
换能器所依据的原理:驱动足在驱动器纵弯陶瓷片的作用下,产生X,Y,Z轴方向的简谐运动,在其三个方向的振动位移分别为x,y,z:

当 W1>0,W2>0,W3>0 时,对其进行三角变换可得:

式(1)表示一个椭球。W1,W2,W3分别为X,Y,Z 3个方向振动幅值;α,β,γ为3个振动方向初相位;ω为驱动足谐振频率。根据超声驱动原理,要使驱动质点做椭圆运动,至少要由两个方向简谐运动合成。因此,在3个方向X,Y,Z振动幅度W1,W2,W3中,至多有一个为0。以W1=0为例,其他情况类似。此时质点运动轨迹:

式(2)与式(1)在YOZ面上的投影相同,当γ-β=π/2时,式(2)表示的轨迹为椭圆。
坐标原点处于电机正中间,换能器被编为1,2,3,4号,其编号和通电情况如下:1号换能器的位置处在XOZ平面的左半平面,其余按逆时针顺序编号。对A相加载激励,在1,3的纵振陶瓷片产生X方向的振动,在D相加载激励可产生Z方向的振动,对A,D两相施加相位差为π/2的激励时就可绕Y方向运动。同理,CD加激励可绕X方向运动,AB加激励可绕Z方向运动。图2为陶瓷片摆放方向和各电极所处位置。各陶瓷片极化方向沿其厚度的方向,同一换能器处于两端的非对称弯振陶瓷片极化方向相反,同端弯振陶瓷片对称的半片极化方向也相反。选用方形陶瓷片仅作为示意使用。

图2 电机陶瓷片和电极片摆放示意图
2 ANSYS有限元设计和分析
对于换能器的模态分析采用ANSYS Workbench,简称WB。
2.1 换能器的模态分析与设计
分析采用不加约束的自由模态,由于胶层和电极片的厚度很小,分析过程中不予考虑,并采用直接法(Direct)进行求解。悬臂梁换能器一阶纵振与二阶弯振模态振型和频率如图3、图4所示。

图3 一阶纵振模态

图4 二阶弯振模态
可以看到,当端盖长为18 mm,宽21 mm,高为21 mm时,换能器一阶纵振和二阶弯振的频率分别是20 907 Hz和20 862 Hz,相差45 Hz,低于简并频率的1%,说明纵弯模态实现了较好的简并。
2.2 圆筒的模态分析
为使圆筒的频率与换能器的频率实现一致(频率简并),对定子圆筒进行基于有限元的分析设计。圆筒采用材料为铝合金,其各项机械性能如表1所示,圆筒内外径分别为80 mm和90 mm,高为21 mm。
对圆筒进行有限元模态分析后,得到六阶径向弯振模态频率为20 911 Hz,与换能器的频率最大相差163 Hz,低于简并频率的1%,说明圆筒的六阶模态频率与换能器的纵弯模态频率实现较好地简并。
2.3 定子的振动模态
基于上述模态数据设计定子,当进行定子有限元模态分析时,会出现模态的频率不简并问题,这是因为当换能器和圆筒组合在一起时,定子整体的刚度增加,使共振频率增大。通过微调换能器端盖的尺寸,可以得到换能器的一阶纵振和二阶弯振所激发出圆筒六阶径向弯振的模态,如图5、图6所示。

图5 一阶纵振激发圆筒六阶弯振

图6 二阶弯振激发的圆筒六阶径向弯振
可以看到,简并后的换能器的纵弯频率分别为20 940 Hz和21 080 Hz。两种模态频率之差为140 Hz,低于简并频率的1%,说明两种模态的频率较好地实现了简并。
通过模态分析最后调整各项参数尺寸,如表1所示。
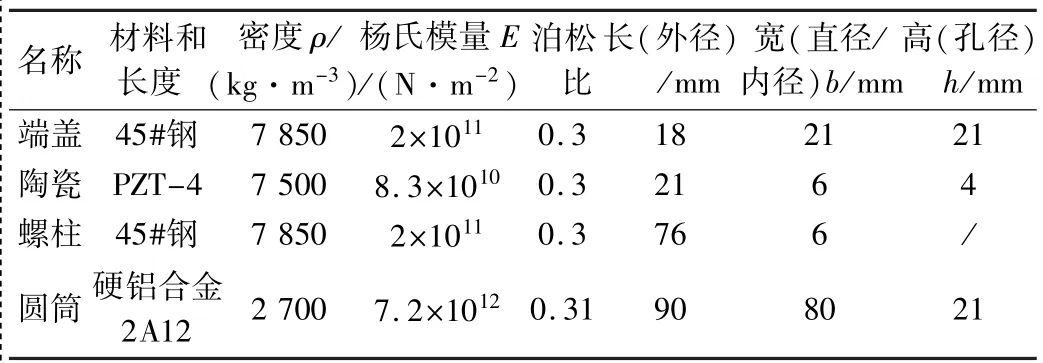
表1 电机定子结构尺寸
3 瞬态分析和谐响应分析
3.1 谐响应分析
谐响分析采用WB分析。由于WB原版环境没有压电分析模块,分析谐响应需要安装ACT_Piezo的压电分析模块。本文采用PZT-4压电陶瓷进行压电分析。
选取其中一个换能器进行谐响应分析,对其纵振压电陶瓷加载均值为100 V交变电压激励,频率响应范围设置在包含20 940 Hz和21 080 Hz在内的20 800~21 100 Hz之间,分析响应频率点数为25个,采用的处理方式为完全处理法(full),full法虽然处理速度较慢,但是相比模态叠加法(mode superposition)可以得到更加细化分析结果。通过分析可以得到换能器在20 945 Hz时振动的位移最大,此时发生共振,如图7所示。

图7 悬臂质点Z方向谐响应
3.2 瞬态分析
这里选取平行于XOY的平面作为研究,其他情况类似。
提取悬臂与圆筒接触处的某质点作为研究对象,对其进行简谐振动测试。根据实际工况[8],对纵弯振陶瓷片施加同一振幅和频率,相位差为π/2,运动形式为Wsin(ωt+φ)的简谐振动,采取的频率为换能器谐振频率ω=2πf,进行瞬态分析。采用WB进行瞬态分析时,最小时间t=1/(20f),这里的f就取值20 945 Hz,时间步数设成1,结束时间设成0.004 s,关闭载荷步自动模式,载荷步时间设成0.000 002 s,时间积分打开。

图8 质点Z方向瞬态分析
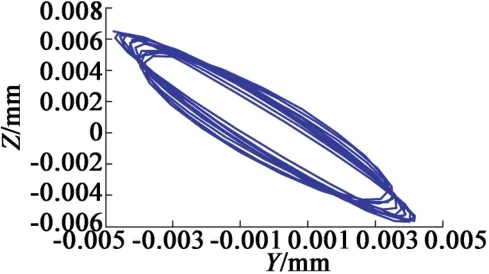
图9 单悬臂梁激励出绕X方向运动轨迹
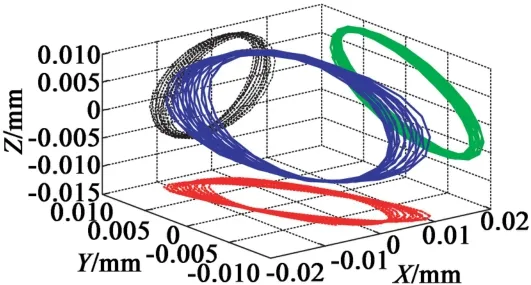
图10 质点三维及各平面运动轨迹
利用同样的方法,提取XOZ面和YOZ面质点,分别进行瞬态分析,取后300个点,利用MATLAB作X-Y-Z和投影到X-Y,X-Z,Y-Z的轨迹图,其中蓝色、红色、黑色、绿色分别为X-Y-Z,X-Y,X-Z,YZ的轨迹图,如图8~图10所示。
通过分析质点运动轨迹可以看出,三个方向的质点运动轨迹都近似于椭圆,而由于弯振是由两个半片陶瓷片的位移差形成,故相比纵振位移,弯振陶瓷片上的位移会比纵振上的位移小一些。且对于单换能器激励而言,质点最大位移为6 μm,而对于双换能器,质点最大位移则为9 μm,振幅增大50%。
4 样机及试验
为验证样机的共振频率是否有效,现对不同频率激励下的电机进行测试,得到频率与电机的转速,如图11所示。可以看出,在20 945 Hz处的电机转速最高,与有限元设计的的电机频率相差仅为135 Hz,说明该设计是有效的。图12即为电机实物图。对样机的纵弯振陶瓷片施加电压来测试电机的电压值与转速的关系。通过对陶瓷片施加激励电压,所测得电压与转速的关系如图13、图14所示。图中电压为有效值,频率为20 945 Hz的正弦激励。

图11 频率与转速的关系

图12 电机实物图

图13 绕Z轴时的电压与转速关系
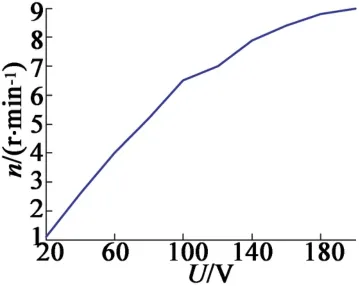
图14 绕X轴时的电压与转速关系
图15、图16为不同转速下的电机输出力矩。可以看出,最大的电机输出力矩为绕X轴时的0.98 N·m,最大转速为9 r/min。当对于电机绕Z轴旋转时,电机的最大力矩为0.32 N·m,最大转速为53 r/min。当对电机3个坐标轴进行旋转,最大转速为8.4 r/min。该转速较其他坐标轴转速都低,原因是3个方向同时加激励时,输出会相互干扰,降低了输出效率。

图15 绕X轴时转速与力矩关系
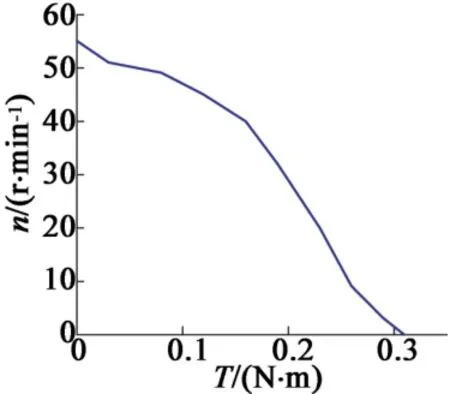
图16 绕Z轴时转速与力矩关系
5 结 语
本文提出了一种基于纵弯复合模态的四换能器式多自由度球型超声波电动机,并分析其工作原理。
运用有限元法设计驱动器的悬臂梁换能器和圆筒,实现两者的模态简并。对驱动器整体进行有限元分析,调整并获得换能器和圆筒的最终尺寸参数,通过对有限元模型进行谐响应分析,得出电机驱动器在20 945 Hz处位移达到最大值,可以实现共振。
最后通过对定子驱动器上的质点进行瞬态分析,得出在前文设定的激励条件下,定子驱动器可以驱动出绕X,Y,Z 3个方向运动,并且质点位移提高50%,从而证明本文提出的电机的可行性和有效性。研制样机并进行力矩转速关系分析,测得样机最大力矩为0.98 N·m,最大转速为53 r/min。
[1] 胡百振,李有光,赵淳生,等.新型纵弯超声波电动机振子的设计与分析[J].压电与声光,2014(3):354-356.
[2] 刘英想,姚郁,陈维山,等.纵振复合双足直线超声波电动机[J].西安交通大学学报,2012,46(8):112-115.
[3] LIN F J,HUNG Y C,CHEN S Y.FPGA-based computed force control system using elman neural network for linear ultrasonic motor[J].IEEE Transactions on Industrial Electronics,2009,56(4):1238-1253.
[4] FRAYSSIGNES H,BRIOT R.Traveling wave ultrasonic motor:coupling effects in free stator[J].Ultrasonics,2003,41(2):89-95.
[5] GEORGE T.Overview of MEMS/NEMS technology development for space applications at NASA/JPL[J].Proceedings of SPIE,2003:136-148.
[6] 罗辞勇,张帆,杜劲.行波型超声波电动机的稳定性分析[J].重庆大学学报,2014,37(2):46-52.
[7] 宋起超,周真.微小型纵弯复合激励式圆筒超声波电动机的设计[J].电测与仪表,2013,50(11):106-109.
[8] 盖学周,王永晔,俞锁龙,等.压电陶瓷振动振幅的测量[J].声学与电子工程,2008(3):27-30.
