永磁同步电动机最大转矩电流比控制方法
2017-05-04高飞燕
高飞燕,刘 华
(南华大学,衡阳421001)
0 引 言
随着人们对能源消耗的重视,纯电动汽车及混合动力电动汽车都得到了各国政府的大力支持。由于永磁同步电动机(以下简称PMSM)结构简单、效率高、体积小等特点,越来越多的电动汽车选用PMSM作为牵引电机。为了更好地提高PMSM效率、降低损耗,获得性能优良的控制效果,对伺服系统的控制方法的研究很有必要。
PMSM驱动控制原理是基于矢量控制,即对定子电流矢量分解的两个分量id,iq进行控制。本文针对PMSM旋转坐标系的d,q轴电感Ld≠Lq的特性,对PMSM系统矢量控制的最大转矩电流比控制(以下简称MPTA)方法进行了较深入研究,通过对Id=0控制、最大转矩电流比控制的结果进行比较,证明使电机转矩在满足要求的条件下MTPA的定子电流最小。文中同时还比较了当电机的折算系数Ke及q轴凸极系数ρ(ρ=Xq/Xd)发生变化时,电机所需要的驱动电流的变化情况。
1 PMSM的数学模型
PMSM在同步旋转坐标系(d-q)下定子电流分解稳态矢量关系图如图1所示。

图1 插入式及内装式PMSM稳态矢量图
PMSM转矩特性如图2所示。

图2 PMSM的转矩特性
根据电机学理论,该电机的电磁转矩方程:

式中:p为电机的极对数;ψf为永磁体产生的磁链;Ld为d轴电感;Lq为q轴电感;id为d轴电流;iq为q轴电流。将该公式标幺值化处理后,可以得到转矩方程:

由式(2)可知,PMSM输出的电磁转矩Tem取决于id和iq两个量的组合,改变id和iq可以改变Tem。要使电磁转矩Tem与电流成线性关系,可以采用Id=0的方法,这样式(2)可以改写:

这种Id=0方法控制简单,此时电磁转矩Tem只与iq有关。
2 最大转矩电流比方法
从图2可以看出,Id=0的控制方法没有有效地利用到电机的磁阻转矩曲线。当电机输出的电磁转矩相同时,电机的定子电流没有达到最小。为了实现这一目的,尽可能使定子电流减小,拟采用最大转矩电流比控制,这是接下来要重点求解的问题。
因为定子电流:

由式(4)可以推导出:

将式(5)代入式(4),可得:

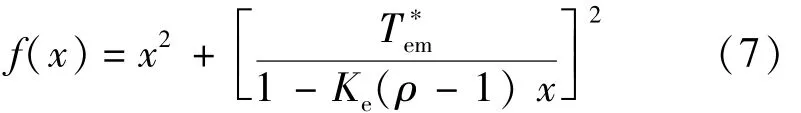
对式(7)求导,最大转矩电流比可以转化为式(7)的极值问题:

令 f′(x)=0,得到:
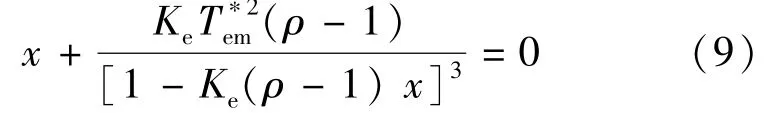
3 最大转矩电流比控制方法分析
利用式(9)的结果,可以对不同的电机设计进行计算对比。在式(9)中,参数Ke和ρ是在电机设计完成后就确定的。下面针对不同的Ke及ρ的组合,对最大转矩电流比控制和Id=0的两种方法进行分析对比,以求得到指导性的结果。
(1)ρ=2,Ke=0.25时的情况
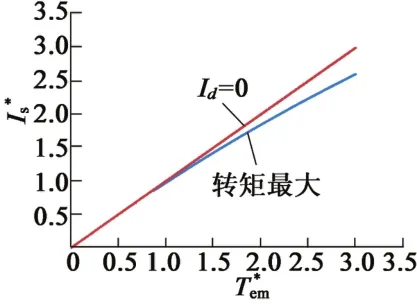
图3 定子电流与转矩的曲线图(,为标幺值)

图4 最大转矩法,曲线图
图5在一定程度上解释了为什么最大转矩电流法在产生同样的转矩情况下需要更小的电流的原因。这主要是因为=0在转矩增加时,其功率因数cos φ迅速变小,导致不得不向变频器要求输出更大的电流;同时可以看到,在高速区运行时,最大转矩电流法对提高驱动器的效率也具有较好的意义。
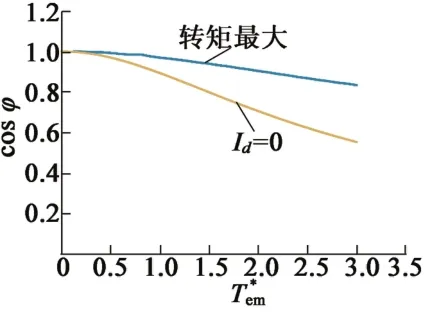
图5 功率因数cos φ与转矩T*em的关系

图6 定子电压与转矩的关系

图7 超前d轴的电角度β与转矩的关系
(2)ρ=2,Ke=0.25及Ke=0.5时的对比
在电机中Ke越小,说明Xd电抗越小,永磁体越厚。
从图8可以看出,在ρ保持不变的情况下,加大永磁体厚度,为获得同样大的转矩,最大转矩电流控制策略所需要的电流不一定会变得更小,单纯的增加永磁体厚度不一定能减小电流值的,这需要在电机设计时先计算好。

图8 变Ke,定子电流与转矩的关系
从图9可以看出,在ρ保持不变的情况下,加大永磁体厚度,为获得同样大的转矩,最大转矩电流控制策略所需要的外端口电压会比永磁体薄时低,这样能把最大转矩电流法应用到更高的速度区域,能提高驱动系统的效率。
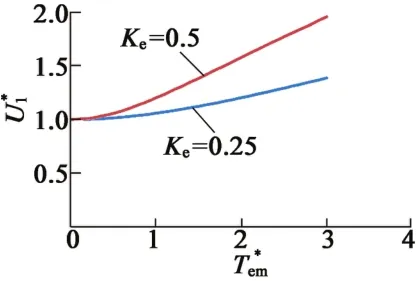
图9 变Ke,定子电压与转矩的关系
从图10可以看出,在ρ保持不变的情况下,永磁体厚度更厚时,电机在整个转矩工作的全程,其功率因数cos φ表现更佳,这样能提高驱动系统的使用效率。

图10 变Ke,功率因数cos φ与转矩的关系
(3)Ke=0.25,ρ=2及ρ=4时的对比
在电机中Ke为常数,说明Xd电抗不变,永磁体厚度不变化,变化的是q轴的磁路,ρ越大,说明q轴的导磁性越好。
从图11可以看出,在永磁体厚度保持不变的情况下,ρ值越大,即电机q轴的凸极率越大,电机的磁阻转矩占总转矩的比重就更大,这样在获得同样大的转矩时,最大转矩电流控制策略所需要的电流就更小,对减少电机的定子铜耗及变频器损耗具有重要的价值。

图11 变ρ,定子电流与转矩的关系
从图12可以看出,当电机的永磁体厚度不变时,q轴的凸极率ρ的变化并不会导致电机在工作过程中的功率因数cos φ出现明显变化,说明电机在永磁体厚度一旦确定之后,电机的主要特性已经确定下来,这是电机设计的关键。

图12 变ρ,功率因数cos φ与转矩的关系
4 结 语
本文研究了PMSM的最大转矩电流比控制方法,该方法可以在给定的定子电流下,输出更大的电磁转矩,从而降低了电机的铜耗,提高了效率。通过合理的工程数学方法,将把PMSM最大转矩电流比的求解转化为了一个数学求取极值的方法,便于工程应用的实施。通过这个方法,对比了=0和最大转矩电流控制策略的差异,同时还比较了当电机永磁体厚度(Ke)发生变化及电机q轴凸极系数ρ变化时,PMSM最大转矩电流控制策略的具体表现,这些结果为使用该方法进行PMSM控制时,在电机设计、驱动器匹配及控制策略在高速区需要注意的转换等方面都具有很好的参考价值和指导意义。
[1] BOSE B K.A high-performance inverterfed drives system of interior permanent magnet synchronous machine[J].IEEE Transactions on Industry Applications,1987,24(6):987-997.
[2] 许家群,唐任远.电动汽车驱动用永磁同步电机数字控制系统[J].辽宁工程大学学报,2005,24(1):76-80.
[3] 张波.永磁同步电动机矢量控制和最大转矩电流比控制[J].华南理工大学学报,1996,24(1):35-39.
[4] BAE B H,SULS K.A compensation method for time delay of full digital synchronous frame current regulator of PWM AC drives[J].IEEE Transactions on Industry Applications,2003,39(3):802-810.
[5] 唐任远.现代永磁电机[M].北京:机械工业出版社,2006.
[6] 李长红,陈明俊,吴小役.PMSM调速系统中最大转矩电流比控制方法的研究[J].中国电机工程学报,2005,25(21):169-172.
[7] 郭庆鼎,陈启飞,刘春芳.永磁同步电机效率优化的最大转矩电流比控制方法[J].沈阳工业大学学报,2008,30(1):1-5.
