基于z标记的灰色GERT多任务项目费用优化研究
2017-05-03朱建军王翯华刘小弟
耿 瑞,朱建军,王翯华,刘小弟,3
(1.南京航空航天大学经济与管理学院,江苏 南京 211106;2.金陵科技学院,江苏 南京 211169;3.安徽工业大学数理学院,安徽 马鞍山 243002)
基于z标记的灰色GERT多任务项目费用优化研究
耿 瑞1,朱建军1,王翯华2,刘小弟1,3
(1.南京航空航天大学经济与管理学院,江苏 南京 211106;2.金陵科技学院,江苏 南京 211169;3.安徽工业大学数理学院,安徽 马鞍山 243002)
研究灰色GERT网络在多任务情况下的费用优化问题。当任务网络中流动的费用变量为时间变量的函数时,针对多个存在依赖关系的任务,运用网络中的z标记探寻各任务之间的时间依赖关系,通过对弹性活动的时间安排进行调整,在保证工期不被延误的前提行下使得整个项目的费用达到优化。以某大型客机客舱环境控制系统为例,对项目中各弹性活动的完成时间和费用进行了研究。
项目管理;多任务;灰色GERT网络;费用优化;最大满意度
1 引言
图示评审技术(Graphical Evaluation and Review Technique,简称GERT网络技术)是系统工程的一个重要分支。在GERT中,工作的各个参数(如时间、费用等) 具有随机性,工作的实现也具有随机性,从而能反映科研、生产和施工中可能遇到的许多复杂情况。经典概率描述的GERT应用范围涵盖系统分析建模[1-2]、产品开发管理[3]、产品质量管理[4-5]、可靠性评估[6]、生产能力评估[7]、资源配置[8]、政策设计[9]等多个领域。但在现实生活中,人们对事物的认知和判断都存在一定的不确定性,于是阮爱清和刘思峰[10]定义了灰色GERT网络,用以表征网络中参数不确定的特征。肖先刚等[11]将不确定区间灰数引入GERT网络,杨保华等[12]利用信号流图原理研究了不确定信息的GERT网络仿真算法;刘思峰等[13]从价值循环流动及价值增值角度研究了一种新的灰色价值流动G-GERT网络;Xu Ruiting等[14]通过建立灰色成功树分析-图示评审技术(GSTA-GERT)找出了复杂产品的评审办法。
但这些GERT网络的研究对象都是单一的任务,没有涉及多个任务并行的情况。为此,我们考虑在描述多个任务引入最常使用的甘特图方法。甘特图最早由 Henrry L.Ganntt于1917年提出。它通常包括项目活动列表、工作开始时间和持续时间,能够清楚地表达各施工过程的开始、结束和持续时间,允许施工过程时间的重叠,在处理多个项目活动时发挥着巨大优势。但同时,甘特图不能显示出各工序之间的相互依赖、相互制约、相互联系的逻辑关系,且主要关注进程管理中的时间,不能综合反映项目的成本等其他因素。我们都知道,除了时间,成本也是项目管理者十分关注的因素,因而对时间-费用的优化研究一直层出不穷。Hajiagha等[15]研究了模糊目标规划和灰数混合模式下的时间、成本、质量的权衡,Haque和Hasin[16]在建模中引入了三角模糊数,解决了项目的时间成本优化问题,Salmasnia等[17]研究了项目时间,成本和质量的鲁棒性调度;在算法方面,Cai Jinling[18]研究了一种改进的人工蜂群算法用以解决最短时间内成本降低,Afruzi等[19]采用多目标帝国主义竞争算法研究了在模式定义和资源受限情况下的时间、成本、质量权衡问题。
本文针对多个时间-费用不确定的任务,将灰色GERT网络与甘特图进行有机结合,运用网络中的z标记探寻各个任务之间的时间依赖关系,通过对任务中的活动进行适当调整,达到优化整个项目费用的目的。
2 分析及建模过程
2.1 经典GERT的基本概念及定义
GERT是指网络计划中活动与活动之间的逻辑关系具有不确定性,且活动的费用和时间参数也不确定,而按随机变量进行分析的网络计划技术。GERT网络的组成部分是定向的支线和逻辑节点,如图1所示。

图1 GERT网络的基本构成单元示意图
经典的GERT网络的解析算法综合了概率论的矩母函数、线性系统的信号流图理论等几方面的理论。通过矩母函数和梅森公式,提供了求解随机网络的工具。
2.2 基于Z标记的GERT过程时间矩母函数
在GERT网络中,若用一个未限定的变量z乘以网络中某一活动的W函数,则称对该活动做了z标记。
定义W(s|j)为当用z做过“标记”的活动经过j次实现时,网络的W函数,或称经过“标记”的活动实现j次时网络的条件函数。在GERT网络分析中,常常需要知道在网络执行中某个节点或者某项活动首次实现的过程时间,而在网络执行中首次到达某一节点的过程时间就是该节点首次实现时间。

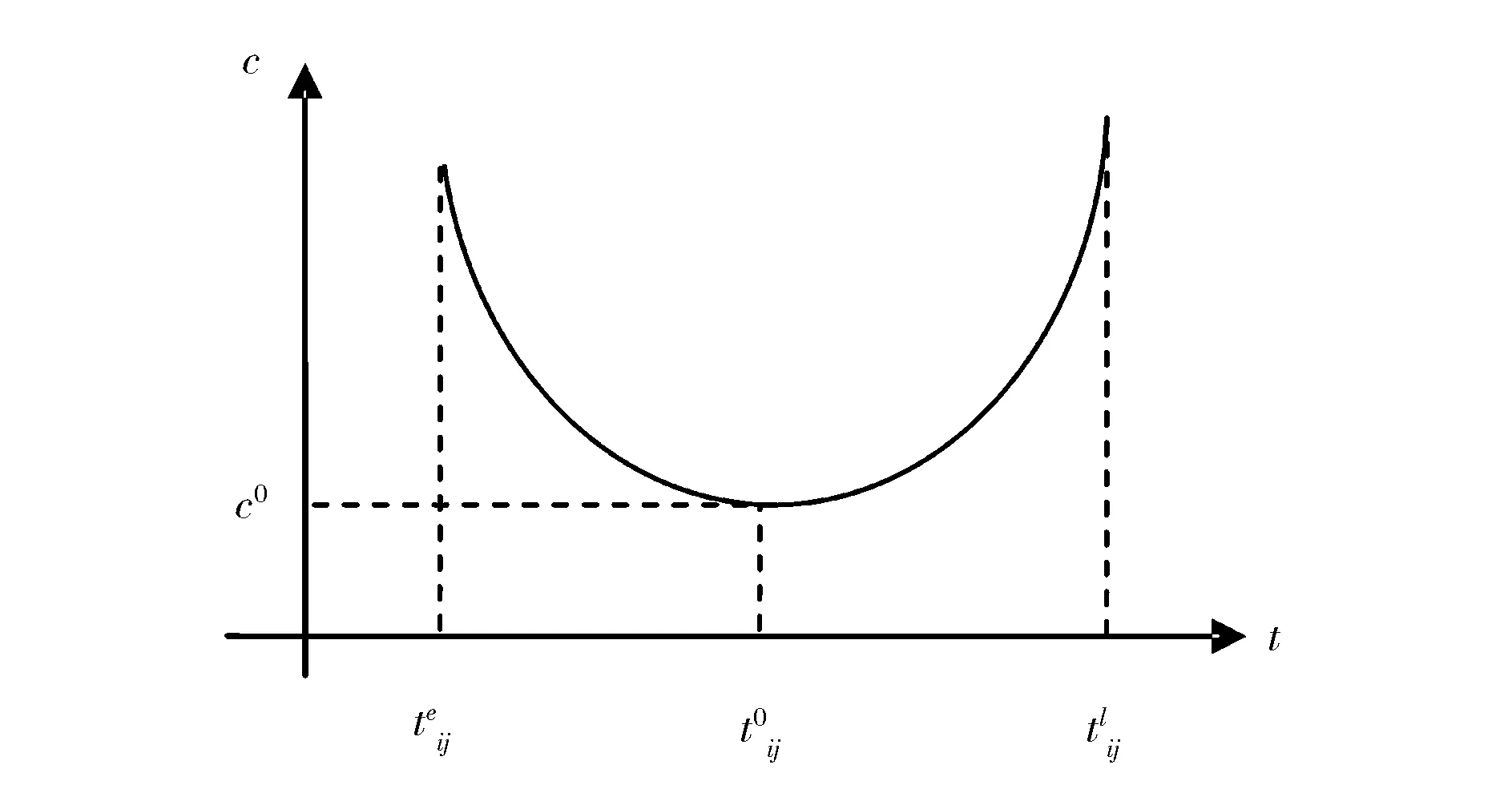
图2 费用与时间的关系图

定理1 若随机变量T的概率密度函数为f(tij),且cij=φ(tij)为单调可导函数,则随机变量C的概率密度函数g(cij)为:
其中,h(cij)是φ(tij)的反函数,
c1=min{φ(-∞),φ(+∞)},
c2=max{φ(-∞),φ(+∞)}。
证明 因为cij=φ(tij)是单调函数,所以cij=φ(tij)存在反函数h(cij)
C的分布函数为:
因而c的概率密度函数g(cij)为:
得证。
2.4 任务活动费用和时间相关的灰色GERT网络模型的解析求解
根据上述分析,当活动费用与时间相关时,运用定理1就可将费用的概率密度函数以时间的概率密度函数表示出来。由此,在GERT网络中引入该关系,并结合GERT网络的解析法的相关定理可得:
定理2 若随机变量T的概率密度函数为f(tij),且cij=φ(tij)为单调函数,则随机变量C的矩母函数函数MC(s)为:
MCij(s)=
证明 因为cij=φ(tij)是单调函数,所以cij=φ(tij)存在反函数h(cij)
根据矩母函数的定义,有:
其中f(tij)是随机变量T的概率密度函数,g(cij)是随机变量C的概率密度函数。
由定理1,
得证。
当已知网络中各个活动的作业时间t和费用c的矩母函数,就可求得GERT网络中含有时间和费用这两个参数的矩母函数为:
如果要考察时间的参数,即令s2=0,有:
如果要考察费用的参数,即令s1=0,有:
有了各活动的矩母函数,便可求得GERT网络中各活动上的传递函数:
当知道各活动的传递函数,即可根据梅森公式求得网络的等价传递函数:
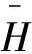
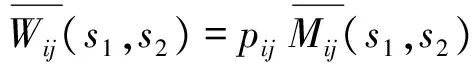
=pijMTij(s1)MCij(s2)
当s1=s2=0时,
由定理2可知,MCij(0)=1


节点i到节点j的等价时间:
节点i到节点j的等价费用:
节点i到节点j的方差:
节点i到节点j的风险度:
2.5 基于Z标记的多任务灰色GERT时间-费用模型求解
2.4中我们讨论了单任务的灰色GERT网络模型的解析求解,它相对独立,可以运用GERT的知识进行分析。但对于大型的工程,往往需要完成不止一个单任务,多个单任务(即多任务)就构成了一个项目。一个项目中的多任务之间往往互相依赖又互相约束,这种依赖和约束体现在时间和资源上。如果多任务中的单任务相对独立,共用资源所导致的互相约束就可适当简化。本文研究的就是这种在时间上互相依赖,但在资源上互相独立的多任务情况。这种情况下,多个任务之间呈现出时间上的相互依赖关系[21],即一个任务的执行以另一个任务的执行为前提,它的简单示例如图3所示。
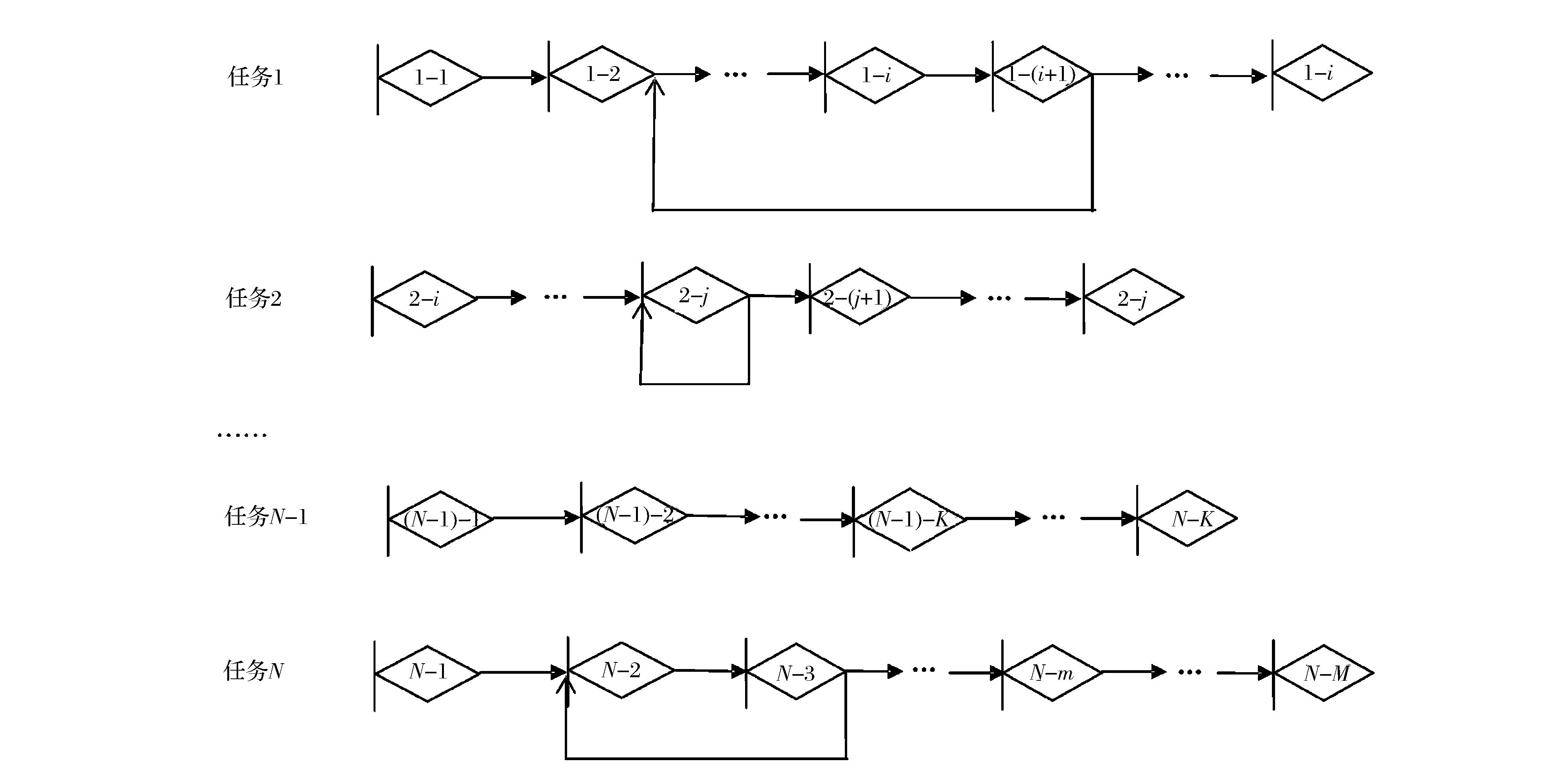
图3 多任务GERT示例图
图3中,任务2需要任务一中的1-i节点开始后方能启动,任务3需要任务二中的2-j节点开始后方能启动……任务N需要任务N-1中的(N-1)-k节点开始后方能启动。这种情况下,任务1中从节点1-1到1-i的过程时间,任务2中从节点2-1到2-j的过程时间,……,任务N-1中的从节点(N-1)-1到(N-1)-k的过程时间都分别决定了下一个任务的开始时间。
定义1 在互相依赖的多任务GERT网络中,我们将影响下一个任务启动的节点称为依赖节点,图3中,节点1-i,2-j,…,(N-1)-k均为依赖节点;将依赖节点以前的过程时间称为固定时间,图3中,t1-1,1-i,t2-1,2-j,…,t(N-1)-1,(N-1)-k均为固定时间;将在依赖节点以后的过程时间称为弹性时间,图3中, (t1-t1-1,1-i),(t2-t2-1,2-j),…, (tN-t(N-1)-1,(N-1)-k),tN-1,N-M均为弹性时间;将弹性时间中的各项活动称为弹性活动。
对于一个有N个任务的项目,整个项目的时间为:T=t1-1,1-i+t2-1,2-j+…+t(N-1)-1,(N-1)-k+ max{tN-1,N-M,(tN-t(N-1)-1,(N-1)-k),…,(t2-t2-1,2-j), (t1-t1-1,1-i)}。其中t1-1,1-i,t2-1,2-j,…,t(N-1)-1,(N-1)-k为每个任务从原点到依赖节点的过程时间,即固定时间;tN-1,N-M,(tN-t(N-1)-1,(N-1)-k),…,(t2-t2-1,2-j), (t1-t1-1,1-i)为每个任务从依赖节点到终点的过程时间,即弹性时间,t1,t2,…,tN为每个任务的完成时间。
项目完成时间T由两部分组成,第一部分T固=t1-1,1-i+t2-1,2-j+…+t(N-1)-1,(N-1)-k是所有固定时间的总和,这部分时间一旦调整将影响整个项目的进度;第二部分T弹=max{tN-1,N-M,(tN-t(N-1)-1,(N-1)-k),…,(t2-t2-1,2-j),(t1-t1-1,1-i)}是所有弹性时间中的最大值,这部分时间由N个任务中最大的弹性时间决定。

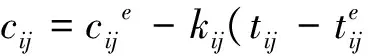
定义2 在多任务灰色GERT网络中,如果对项目中各任务的时间进行约束,则称该网络为时间输出受控的随机网络TRMG-GERT(TimeRestrictedMultitaskingGreyGraphicalEvaluationandReviewTechnique)。
TRMG-GERT网络模型中,存在多个单任务的GERT网络,单个任务的图形一般由箭线、节点、流以及约束条件四个要素组成,其基本构成单元如图4所示。
图4 TRMG-GERT网络的基本构成单元示意图

在本文研究的背景中,为了保证项目工期不被延长,只能对弹性活动进行调整,使得总工期不变,总费用得到优化。为了描述客户对各个任务的要求,引入客户满意度μ,应满足下列条件:当限制被严重违反时,μ=0;当限制完全满足时,μ=1;随着限制从被严重违反到完全满足时,μ从0单调地增加到1。
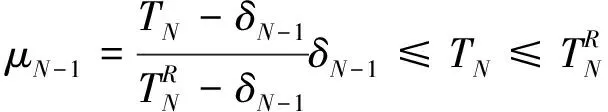

图5 时间的满意度函数

定义4 对于任务N时间风险度,定义其时间风险满意度为μN-2,如图6所示:

图6 时间风险度的满意度函数
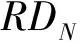
令总体满意度为μN,则有μN=ωN-1μN-1+ωN-2μN-2(ωN-1,ωN-2∈[0,1],ωN-1+ωN-2=1),ωN-1,ωN-2为客户针对时间和时间风险度分别给出的权重,可以通过AHP层次分析法、Delphi法等得到。
为了使客户的满意度高,即得到如下模型:
maxμN
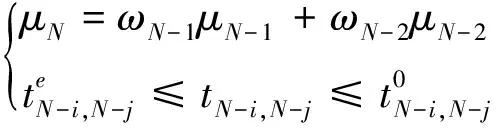
其中N表示需要优化的任务。
由此,我们从最大化客户满意度的角度,建立基于z标记的灰色GERT多任务费用优化模型,从而能够在保证项目工期不被延长的条件下降低费用。
2.6 TRMG-GERT模型的求解步骤
(1)根据项目的基本特征,构建TRMG-GERT网络,确定多任务之间的时间依赖关系。
(2)收集赶工作业时,网络中活动ij的基本参数tije,cije,应用信号流图的梅森公式来确定项目时间TE;通过对依赖节点进行z标记,确定各任务的固定时间和弹性时间。
(3)以区间灰数t(⊗)ij∈[tij0,tije]表征弹性活动ij的完成时间,cij可由与tij的函数关系求得。
(4)结合客户对时间的要求TR,建立客户满意度μ优化模型,用模糊规划求出符合最佳满意度的精确网络参数tij,cij可进一步由与tij的函数关系求得。
3 算例分析
某大型客机正在研制环境控制系统。由于客机的研制过程一再推迟,目前研制方正全力赶工,投入大量的资金和人力,多条生产线并行,以期能尽快完成项目。在赶工状态下,项目的研制虽然能够以最快速度进行,但花费较大。在项目研制过程中,适当延长活动时间可以降低赶工的费用。为了能够在保证项目工期的前提下适当节省费用,需要对项目中的任务进行重新规划和安排。
现以研制过程中一条研制生产线“制冷组件-温度控制系统-环境控制系统”为例,项目的三个任务分别为(1)制冷组建的研制;(2)温度控制系统的研制;(3)环境控制系统的研制。其中,环境控制系统依赖于温度控制系统,温度控制系统依赖于制冷组件,其研制过程的TRMG-GERT网络模型如下图7、8、9所示。

图7 某大型客机制冷组件研制GERT网络

图8 某大型客机温度控制系统研制GERT网络
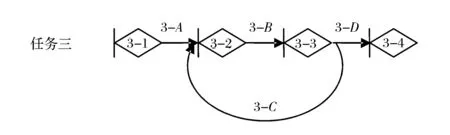
图9 某大型客机温度控制系统研制GERT网络
三个任务中,任务二需要任务一中的1-3节点开始后方能启动,任务三需要任务二中的2-4节点开始后方能启动。这种情况下,节点1-3和节点2-4首次实现的过程时间分别决定了任务二和任务三的开始时间。

由于客舱环境控制系统的研制在国内外已经具备了一定的经验,根据目前的研制进展,通过对历史经验数据的统计分析,同时通过专家意见Delphi法,可对各活动的概率以及赶工状态下的作业时间和费用做出估计,并给出非赶工状态下时间和费用可能的范围。若多个专家组出的估计值不一致,可运用群决策和数据融合的相关方法进行处理,以便获得一个满意的估计值,在此不做赘述。某大型客机客舱环境控制系统项目中三个任务的活动参数见下表1、2、3。
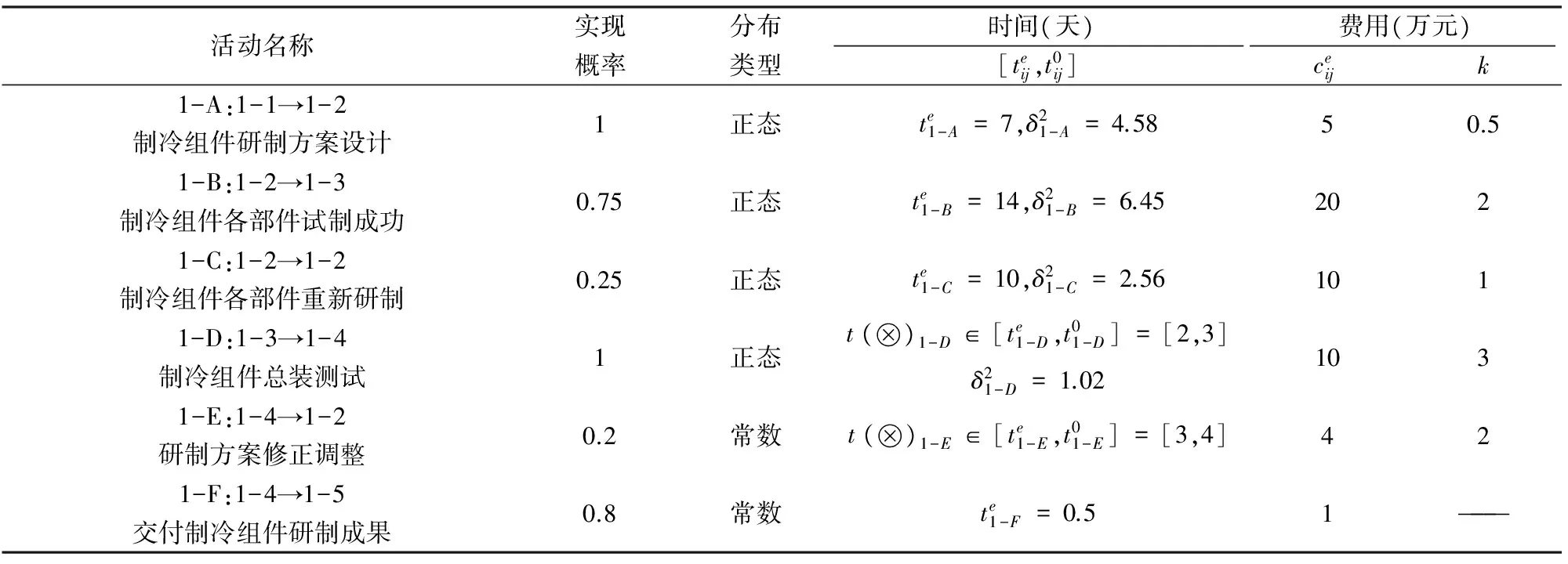
表1 制冷组件研制活动参数表
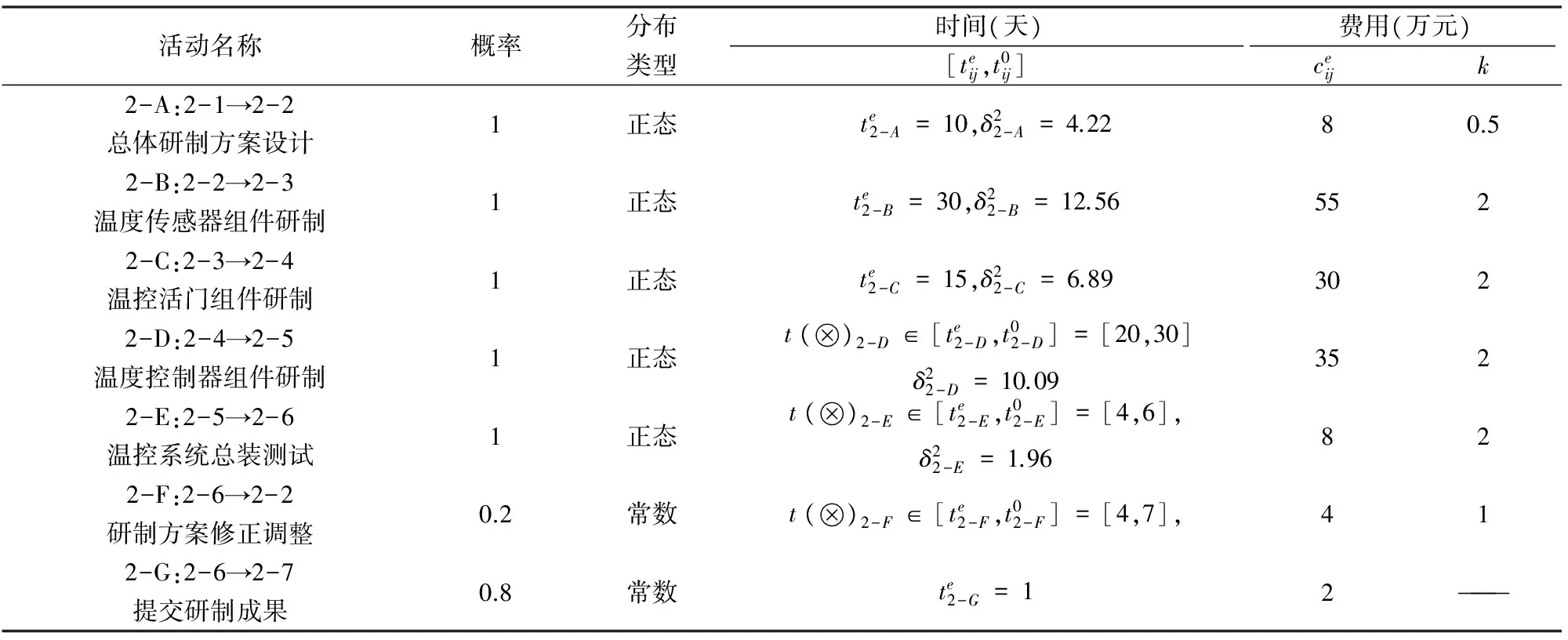
表2 温度控制系统研制活动参数表

表3 环境控制系统研制活动参数表
以任务一为例,成功的概率P1=1
等价传递函数
等价矩母函数
将te,ce代入,可求得该网络在赶工状态时的时间及费用:

将t0,c0代入,可求得该网络在调整弹性时间至最佳状态时的时间及费用:

在节点1-3引入z标记,得到由任务一的节点1-1到达节点1-3的等价W函数为:
由此可得:

同理,可求得各个任务的时间及费用如表4所示。

表4 各任务参数表
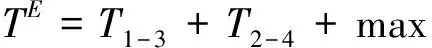

为保证工期不改变,可以对任务一和任务三中的弹性活动进行时间的重新规化。构建时间及时间风险度满意度的加权最优化模型。即:
maxμN
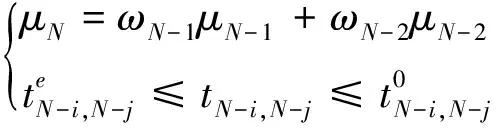
其中,N分别表示1和3,即任务一和任务三。μN-1是任务N时间的满意度,μN-2是任务N时间风险的满意度。以任务一为例,根据客户需求,给出ω1-1=0.8,ω1-2=0.2,δ1-1=32.4,δ1-2=47.4%,δ1-3=46.7%,代入最优化模型可分别求得任务一的优化方案,类似可求得任务三的优化方案,如下表5、6所示。
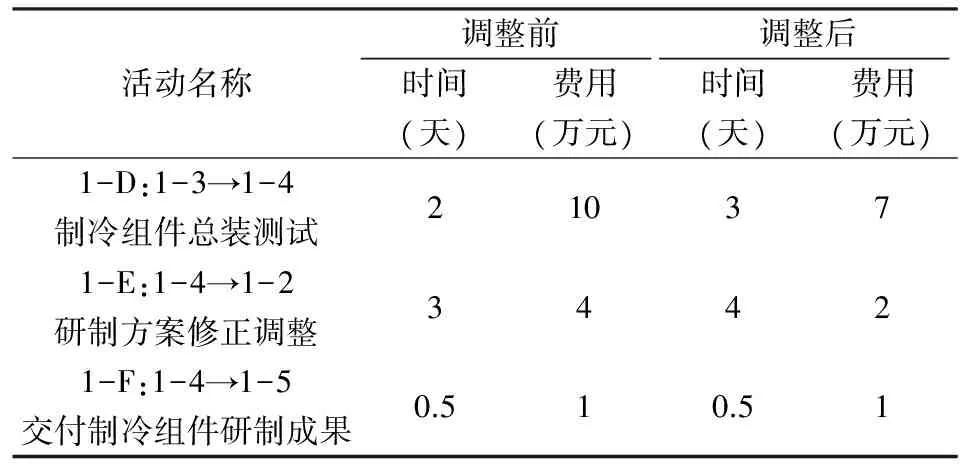
表5 制冷组件研制弹性活动参数调整前后对比
此时项目的总工期T=122.6=TE,工期没有延长,而费用C=250.9 表6 环境控制系统研制弹性活动参数调整前后对比 本文考虑了现实情况中一种多任务并行的费用优化问题。通过引入甘特图的思想,解决了多任务并行的问题;通过利用GERT网络描述任务,弥补了甘特图只能反映时间的缺陷。在假定项目中各项活动的费用与时间线性相关的前提下,借助时间的分布导出了费用的分布。同时利用GERT网络中的z标记,求解出各依赖节点的过程时间,研究了弹性时间部分的费用优化问题,从而时间了在保证项目总工期不被延期的条件下,通过适当延长各个弹性活动的时间,争取了费用的降低。为了处理方便,本文研究了费用和时间线性相关的情况,但现实情况中由于项目本身的特点,费用与时间的关系也将呈现更加复杂的关系。如何系统地考虑时间与费用之间的复杂关系,求解非线性情况下多任务的费用优化问题是今后需要继续深入的方向。 [1] Abdi R, Ghasemzadeh H R, Abdollahpour S, et al. Modeling and analysis of mechanization projects of wheat production by GERT networks [J]. Agricultural Sciences in China, 2010, 9(7): 1078-1083. [2] El-Sherbeny M. GERT analysis for a dissimilar two-engine aeroplane model with CCF, human error and PM [J]. The International Journal of Quality & Reliability Management, 2010, 27(3): 378-390. [3] León H C M, Farris J A, Letens G et al. An analytical management framework for new product development processes featuring uncertain iterations [J]. Journal of Engineering and Technology Management, 2013, 30(1): 45-71. [4] Xu Ruiting, Fang Zhigeng, Sun Jinyu. A grey STA-GERT quality evaluation model for complex products based on manufacture-service dual-network [J].Grey Systems: Theory and Application, 2014, 4(2): 195-206. [5] 刘远,方志耕,刘思峰, 等. 基于供应商图示评审网络的复杂产品关键质量源诊断与探测问题研究[J]. 管理工程学报, 2011,25(2):212-219. [6] Lin Kuoping, Wu Mingjia, Hung Kuochen, et al. Developing a Tω (the weakest t-norm) fuzzy GERT for evaluating uncertain process reliability in semiconductor manufacturing [J]. Applied Soft Computing, 2011, 11(8): 5165-5180. [7] Wang C N, Yang G K, Hung K C, et al. Evaluating the manufacturing capability of a lithographic area by using a novel vague GERT [J]. Expert Systems with Applications, 2011, 38(1): 923-932. [8] 方志耕, 杨保华, 陆志鹏, 等. 基于Bayes 推理的灾害演化GERT 网络模型研究[J]. 中国管理科学, 2009, 17(2):102-107. [9] 金振鑫,陈洪转,胡海东.区域创新型科技人才培养及政策设计的GERT 网络模型[J]. 科学学与科学技术管理, 2011, 32(12):144-152. [10] 阮爱清,刘思峰. 灰色GERT网络及基于顾客需求的灰数估计精度[J]. 系统工程, 2007,25(12):100-104. [11] 肖先刚, 方志耕, 赵云龙. 基于GERT网络改进算法的某型船舶制造周期问题研究[J]. 物流科技, 2009,(4):25-28. [12] 杨保华,方志耕,张娜,等. 基于多种不确定性参数分布的U_GERT网络模型及其应用研究[J]. 中国管理科学, 2010, 18(2):96-101. [13] 刘思峰,俞斌,方志耕,等. 灰色价值流动G-G-GERT网络模型及其应用研究[J]. 中国管理科学, 2009, 17(S1):28-33. [14] Xu Ruiting, Fang Zhigeng,Sun Jinyu. A grey STA-GERT quality evaluation model for complex products based on manufacture-service dual-network [J]. Grey Systems: Theory and Application, 2014, 4(2):195-206. [15] Hajiagha S H R, Mahdiraji H A, Hashemi S S. A hybrid model of fuzzy goal programming and grey numbers in continuous project time, cost, and quality tradeoff [J]. The International Journal of Advanced Manufacturing Technology, 2014, 71(1):117-126. [16] Haque K M A, Hasin M A A. Fuzzy based project time-cost optimization using simulated annealing search technique [J]. International Journal of Information Technology Project Management, 2014, 5(1):90-103. [17] Salmasnia A, Mokhtari H, Abadi I N K. A robust scheduling of projects with time, cost, and quality considerations [J]. The International Journal of Advanced Manufacturing Technology, 2012, 60(5):631-642. [18] Cai Jinling, Zhu W, Ding Haijun, et al. An improved artificial bee colony algorithm for minimal time cost reduction [J]. International Journal of Machine Learning and Cybernetics, 2014, 5(5):743-752. [19] Afruzi E N, Najafi A A, Roghanian E, et al. A multi-objective imperialist competitive algorithm for solving discrete time, cost and quality trade-off problems with mode-identity and resource-constrained situations [J]. Computers & Operations Research, 2014,50: 80-96. [20] Ghasemzsdeh F, Archer N,Iyogun P. A zero- one model for project portfolio selection and scheduling[J]. Journal of Operational Research Society, 1999, 50(7): 745-755. [21] Hegazy T. Optimization of construction time-cost trade-off analysis using genetic algorithms [J]. Canadian Journal of Civil Engineering, 2011, 26(6):685-697. [22] GoldrattE M. Critical chain [M].Great Barrington: The North River Press,1997. Optimization of the Costs in Multi-tasking Grey GERT Based on z Tags GENG Rui1,ZHU Jian-jun1, WANG He-hua2,LIU Xiao-di1,3 (1.School of Economics and Management, Nanjing University of Aeronautics and Astronautics, Nanjing 211106, China;2.Jinling Institute of Technology, Nanjing 211106, China;3.School of Mathematics and Physics, Anhui University of Technology, Ma'anshan 243002, China) During a project, the period and the cost are often what the customer pays closo attertion to. For a multitask one, the ultimate completion time depends the slowest task. As a result, there is certain flexibility for those tasks that could be finished before the last one. We can make good use of the flexible time to reduce the overtime pay and equipment upgrade fee etc. so that the overall expense can be reduced. Based on the previous research, there is a certain relationship between time and expense. For multiple dependent projects, better time schedule could not only slow down the whole project but also reduce the overall expense. In this paper, this problem is addressed by GERT network. To be more specific, in the GERT network, the relationship between the progresses of each task is traced via Z-tags. The fixed time and flexible time are also defined, and the experiments of the expense are conduced involved in flexible time and fixed time respectively. When the flowing money in task network becomes a function of time, we can optimize the overall project fee can be optimized while avoiding delaying the whole project by adjusting the time schedule. Moreover, the customer content maximization (CCM) method is used to optimize the project fee. The CCM is defined as the weighted sum of expense content and risk content. At last, the project of one large passenger cabin environmental control system and work on the flexible time and expense of each task are investigated. It is found that our method is able to make full use of the flexible time of each task so as to reduce the overall project fee, which is full of practical values. project management; multi-tasking; grey GERT network; optimization of the costs; maximum satisfaction 2014-12-03; 2017-01-21 国家自然科学基金资助项目(71171112);高校哲学社会科学重点项目(2012ZDIXM007);国家自然科学青年基金(71502073);教育部人文社科基金(14YJC630120) 耿瑞(1988-),女(汉族),江苏人,南京航空航天大学经济管理学院硕士研究生,研究方向:项目管理,E-mail:grace881028@163.com. 1003-207(2017)04-0133-10 10.16381/j.cnki.issn1003-207x.2017.04.016 C935 A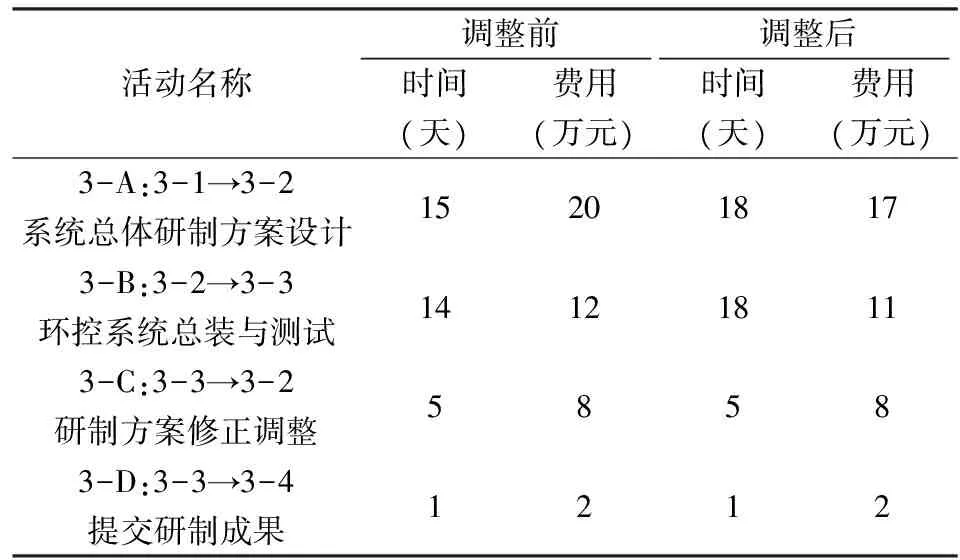
4 结语
