基于Tate简化侵彻模型的率相关相似律研究

段士伟, 李 平

(1 安徽工业大学机械工程学院, 安徽马鞍山 243032; 2 安徽工业大学管理科学与工程学院, 安徽马鞍山 243032)

0 引言

弹体对防护材料的侵彻问题一直是武器研发和工程防护研究部门所关注的重点。由于靶体规模较大或材料较昂贵,用小尺寸模型进行抗侵彻规律研究就成为比较常用的实验方法。因此对于抗侵彻规律的相似律研究具有比较重要的学术意义和工程价值,国内外许多学者在这方面曾开展过大量研究[1]。文中基于李永池等在流体动力比拟的基础上提出的修正Tate简化侵彻模型[2](如图1所示),对考虑弹体和靶板应变率效应时的相似律问题进行了模拟计算,得到了修正的几何相似律公式。

图1中面积为A0的面A0A0左侧为弹体无变形部分,此区域长l;面积为A1的面A1A1左侧A0A0A1A1区域为弹体产生塑性变形蘑菇头区域;环形弹渣反弹面A1B1面积记为B1;侵彻交界面A2A2面积记为A2;面积为A3的A3A3面为靶板破碎前阵面。

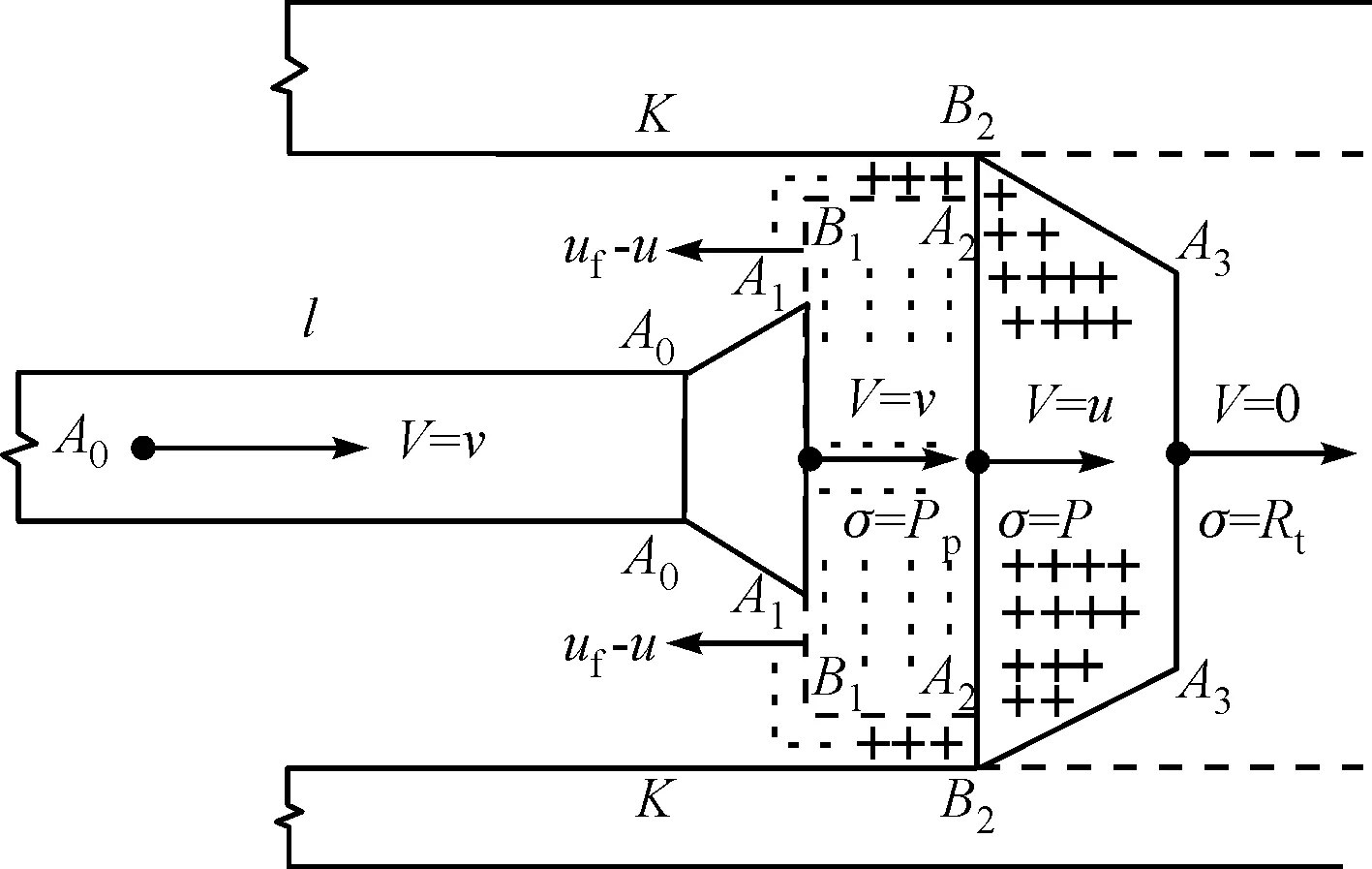
图1 简化侵彻模型

1 模型简要介绍

根据文献[2]侵彻问题的常微分方程组为:

(1)

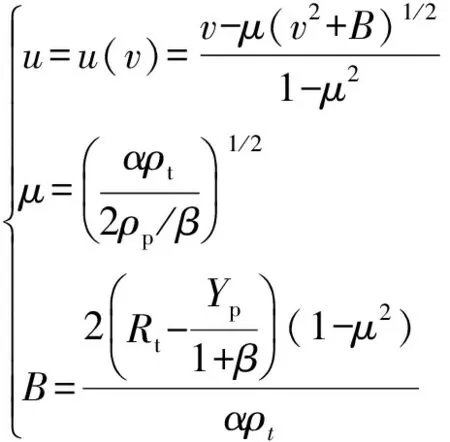
(2)

考虑应变率效应时,将弹体破碎应变,弹体破碎强度和靶板破碎强度的应变率分别设为:

2 相似律分析

由式(1)～式(3)可见,总侵彻深度是由以下因素决定的(忽略了开坑阶段,只考虑准稳定阶段):

当模型与原型具有相同的弹体和靶体材料且满足几何相似的条件下,上式转化为:

(4)

在忽略弹靶应变率效应时,在相同的弹体速度并满足几何相似大小不同的原型和模型中所引起的无量纲侵彻深度H/l0是相同的,即:

(5)

其中下标m和y分别表示模型和原型。此即时率无关材料高速侵彻的几何相似律。

但是式(4)中由于材料应变率的存在,几何相似律并不严格成立。需要注意的是式(4)的具体形式并不能单纯地由量纲分析方法而得出,必须由实验或者数值模拟计算的方法来确定。

3 计及材料应变率效应的影响

数值计算所采用的材料参数取自文献[2-4],见表1。

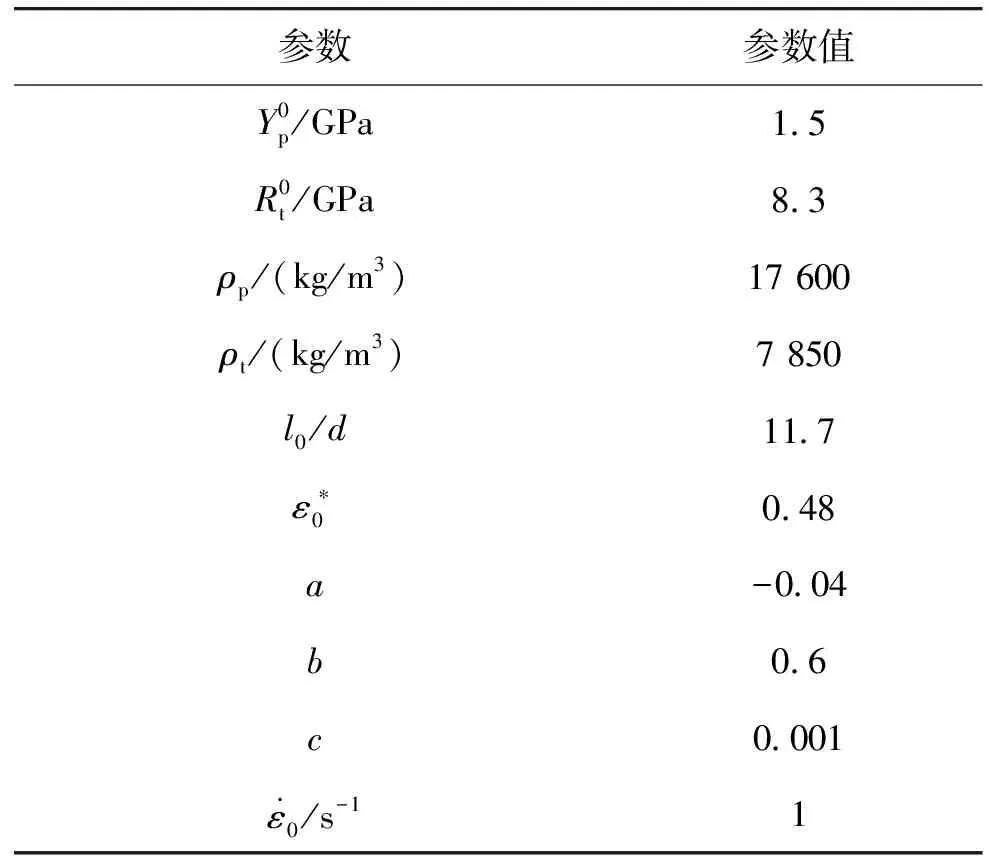
表1 弹靶材料参数

针对式(1),应用Runge-Kutta算法,计算得到了初始入射速度为1 300 m/s下,只考虑靶体应变率效应、只考虑弹体应变率效应以及同时考虑靶体和弹体应变率效应情况下,不同弹长的最大侵彻深度值,分别如表2、表3和表4所示。对表2、表3和表4所得数据进行任意组合可得到Hy/Hm和Ly/Lm之间的关系,分别如图2、图3和图4所示。

图2、图3和图4中45°虚线为严格的几何相似律成立条件下Hy/Hm与Ly/Lm之间的关系。

由图2可见,同样弹速的情况下,由于几何相似性,随着弹长的增加,弹体直径也相应增加,导致靶板应变率相对于小弹长时的应变率有所降低,从而使靶的相对破碎强度有所降低(式(3c)),导致上图中随着原型和模型弹长比的增加,原型和模型侵彻深度之比向上偏离45°虚线。

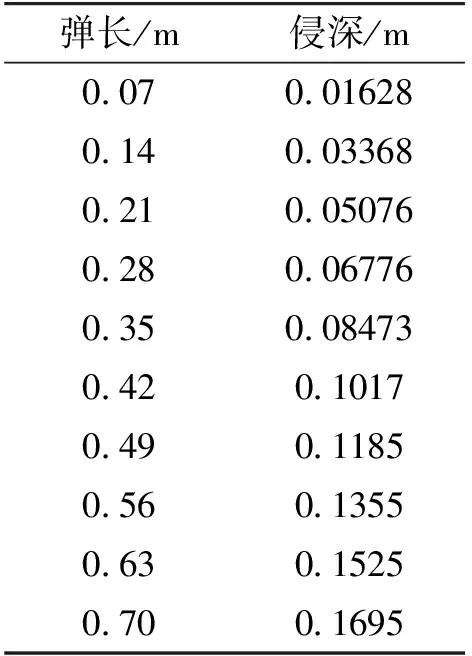
表2 只考虑靶体应变率效应

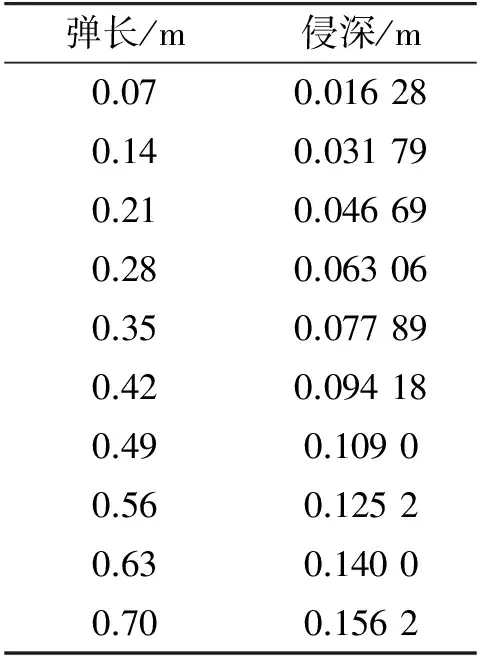
表3 只考虑弹体应变率效应

表4 同时考虑弹靶应变率效应

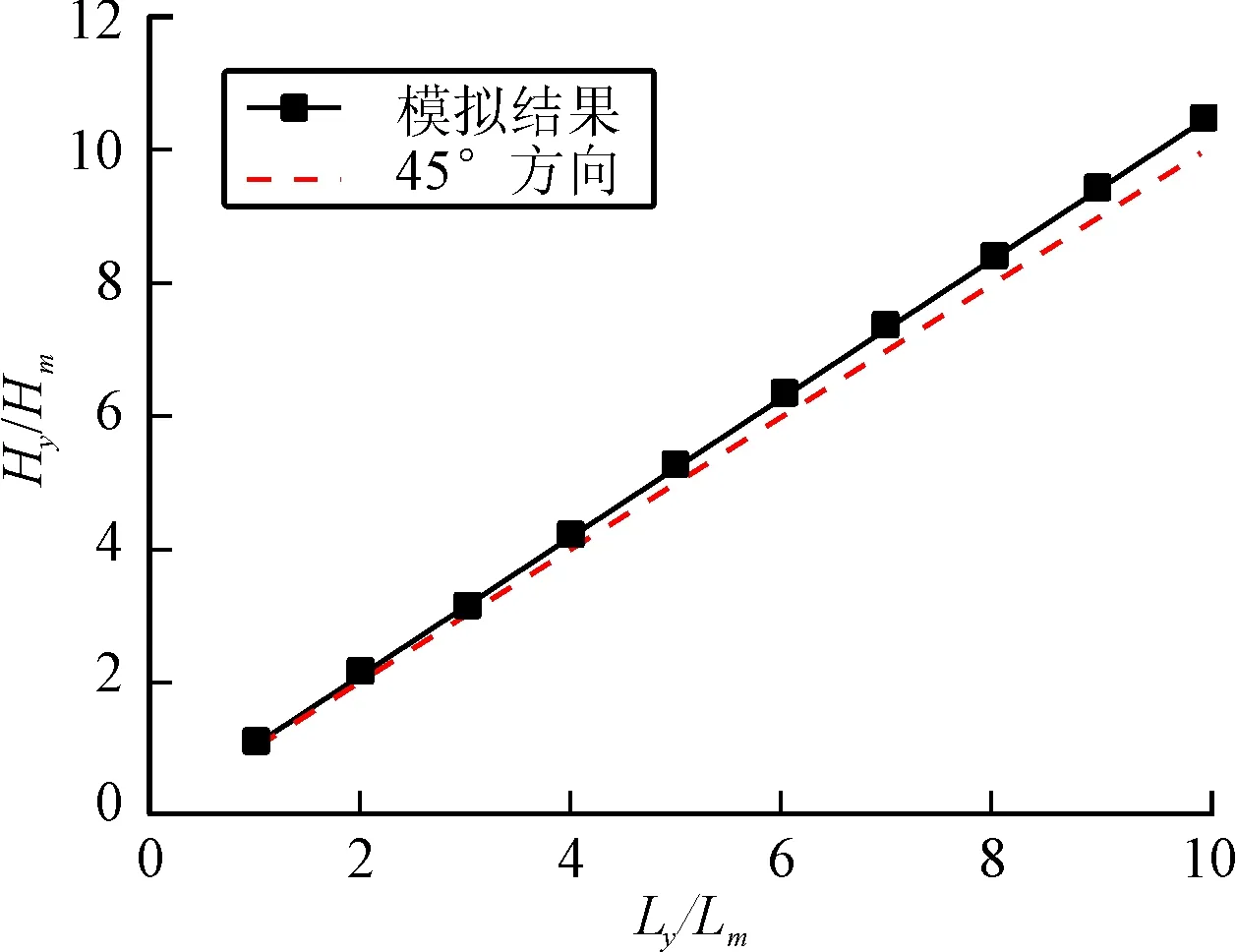
图2 只考虑靶体应变率效应

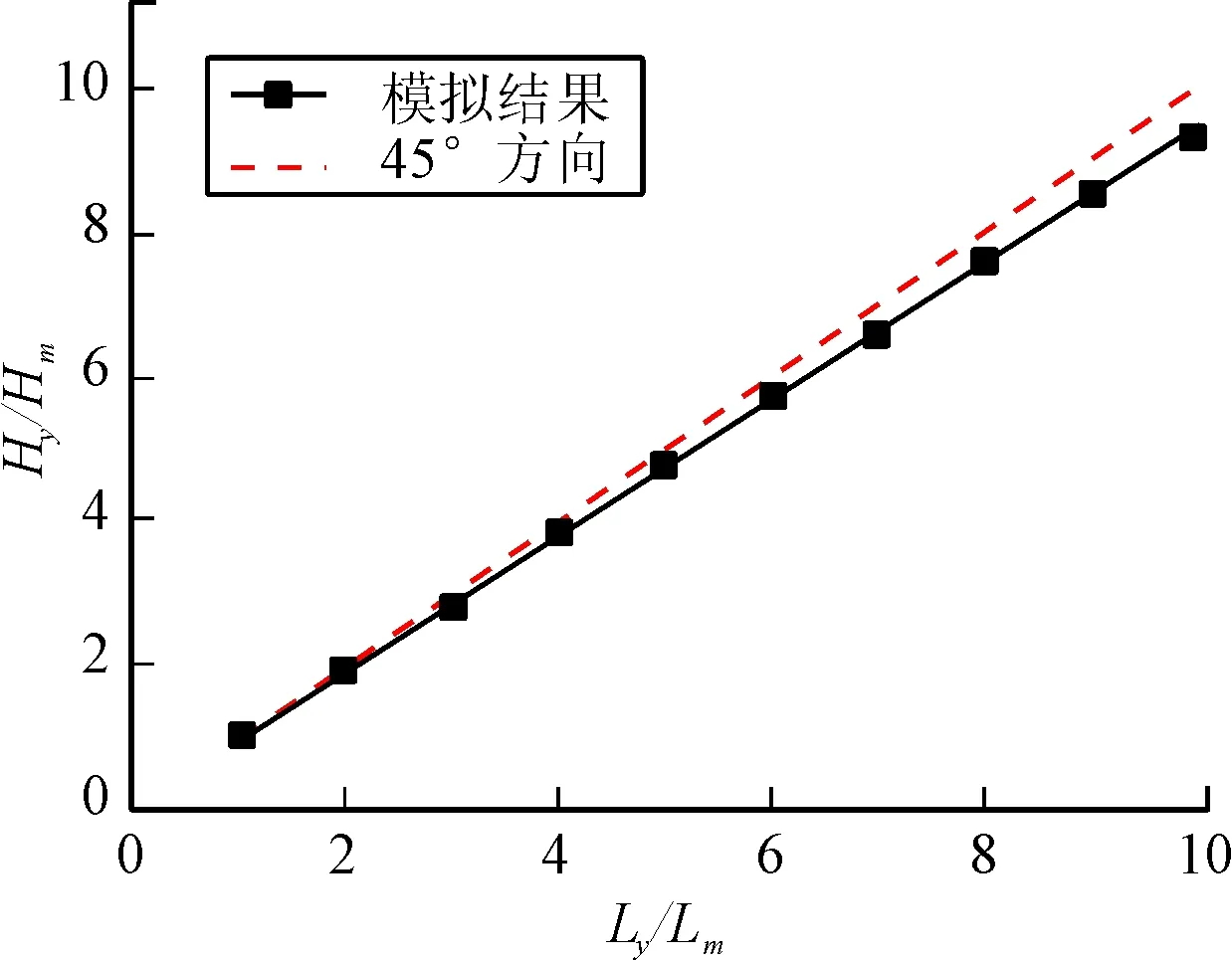
图3 只考虑弹体应变率效应

图3中,同样弹速的情况下,由于几何相似性,随着弹长的增加,弹体应变率相对于小弹长时的应变率有所降低:(a)从而使弹体的相对破碎强度有所降低,弹体的破碎强度决定了弹体受到的阻力,随着破坏强度的降低,弹体受到的侵彻阻力随之减小,从而有利于侵彻;(b)同时弹体的相对破碎应变有所增加(a<0),破碎应变的增大,使得蘑菇头的面积增大,不利于侵彻。(a)、(b)同时作用的结果是不利于侵彻,导致上图中随着原型和模型弹长比的增加,原型和模型侵彻深度之比向下偏离45°虚线。

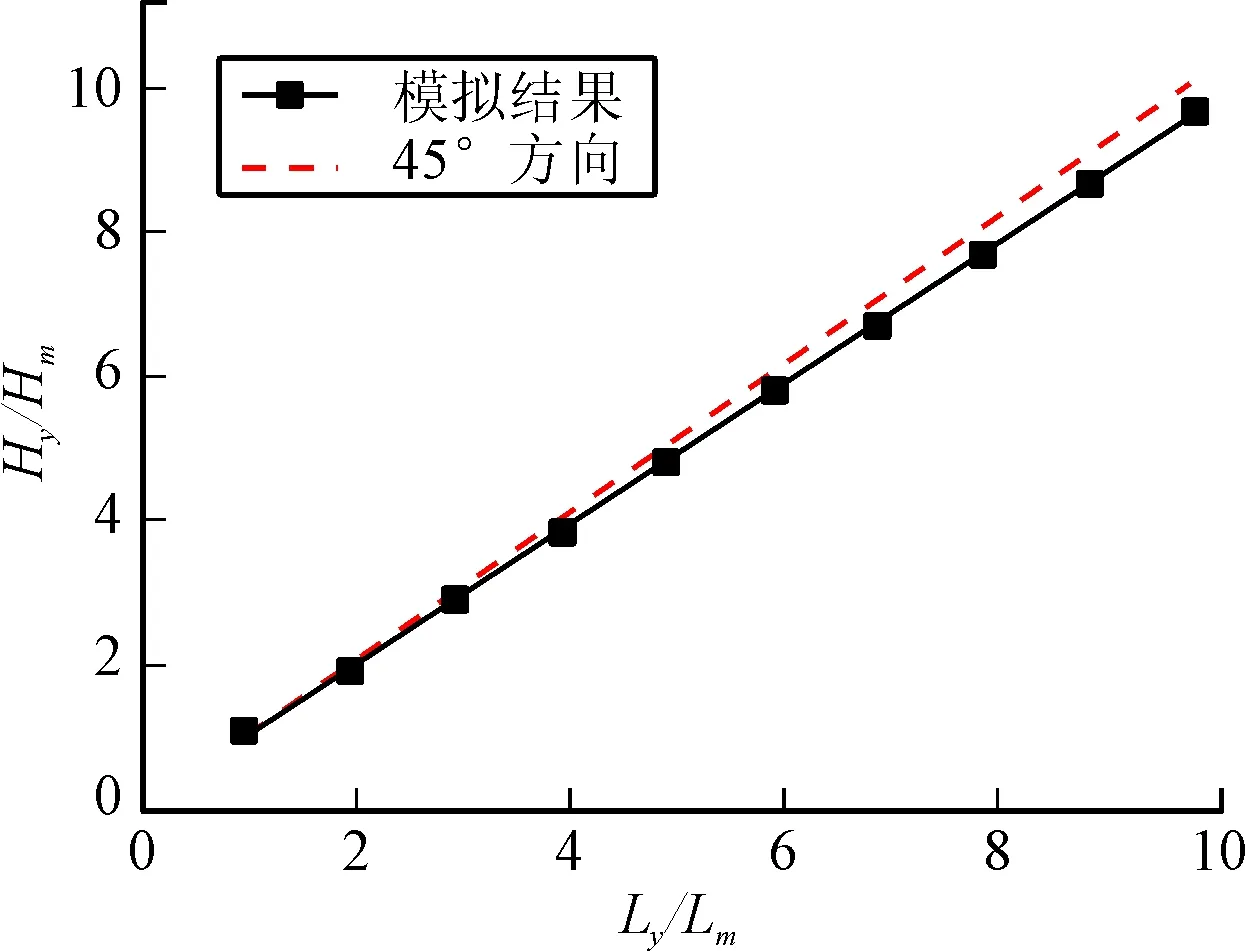
图4 同时考虑弹靶应变率效应

由图4可见,在1 300 m/s弹速之下,Hy/Hm与Ly/Lm之间有比较明显的线性关系,拟合得到:

Hy/Hm=0.037 54+0.949 18·Ly/Lm

(6)

数值计算中,应变率取为弹体侵彻速度与弹体直径的4倍之比,同时应变率因子较小,所以当速度变化不大时(小于10倍),随着入射速度的变化,式(6)中系数的改变并不明显。

与几何相似律(H/l0)m=(H/l0)y比较,在同时考虑弹、靶应变率效应的影响下,几何相似律发生了少许变化。较小的缩尺比λ=Ly/Lm下,几何相似律是基本成立的,随着缩尺比的增大,应变率效应对相似律的影响越来越明显。

4 结论

文中对弹体高速侵彻靶板的率相关相似律进行分析研究。利用数值计算,研究了弹体和靶体材料应变率效应对侵彻深度的影响。

1)随着缩尺比的增加,材料的应变率效应越来越明显,在相关分析中应该考虑材料的应变率效应;

2)通过对相同弹速下靶板抗侵彻问题进行数值计算,结果显示,侵彻深度之比与缩尺比呈现出线性关系,在同时考虑弹、靶应变率效应的影响下,几何相似律发生了少许偏移;

3)通过拟合得到了修正的几何相似律公式。

文中结论对相关侵彻相似实验的设计有一定的参考意义。

参考文献:

[1] 宋梅利, 李文彬, 王晓鸣, 等. 弹体高速侵彻效率的实验和量纲分析 [J]. 爆炸与冲击, 2016, 36(6): 752-758.

[2] 王道荣. 高速侵彻现象的工程分析方法和数值模拟研究 [D]. 合肥: 中国科学技术大学, 2002

[3] ROSENBERG Z, DEKELE E, HOHLER V, et al. Hypervelocity penetration of tungsten alloy rods into ceramic tiles: experiments and 2-D simulations [J]. International Journal of Impact Engineering, 1997，20(6/7/8/9/10): 675-683.

[4] 孙庚辰, 吴锦云, 赵国志, 等. 长杆弹垂直侵彻半无限厚靶板的简化模型 [J]. 兵工学报, 1981(4): 1-8.

[5] TATE A. A theory for the deceleration of long rods after impact [J]. Journal of the Mechanics and Physics of Solids, 1967，15(6): 387-399.