不同跨度地下洞室弹体侵彻效应数值模拟研究

刘绍鎏, 孙惠香, 王晓龙 ,张 悦, 黄文文, 康 婷, 张 玺

(1 空军工程大学, 西安 710038; 2.94900部队, 福建漳州 363000; 3 93199部队, 哈尔滨 150001)

0 引言

第二次世界大战以来,武器的威力和打击精度迅速提高,精确制导武器在现代高技术战争中的地位日益凸显,受到世界各国的高度重视。弹体侵彻一定深度后爆炸耦合入地的能量会大幅增加,破坏效应是触地爆炸的数倍甚至数十倍,对地下目标构成严重威胁[1]。精确制导武器的侵彻爆炸效应已成为地下结构设计必须重点考虑的问题。

近年来,国内外学者对弹体的侵彻效应做了大量的研究,Gold[2]对高速弹体侵彻混凝土的侵彻阻力问题进行了数值模拟,并探讨了不同材料模型对其侵彻响应结果的影响;Warren[3]等将空腔膨胀理论分析方法和数值模拟技术有机结合,采用复杂的混凝土本构模型理论对动态过程进行了分析;郑文力等[4]对钻地弹侵彻高强度混凝土靶进行了数值模拟研究,并对侵彻过程中装药的过载问题进行了分析;徐干成等[5]对地下洞室围岩外加固抗炸弹侵彻性能进行了大量研究。然而,由于赋存环境的特殊性和侵彻效应的特点,地下洞室在弹体侵彻作用下的动力效应研究较少,所以文中对弹体侵彻作用下不同跨度地下洞室的受力情况和位移响应进行研究,为改进防护结构设计方法及促进防护技术发展提供理论依据。

1 数值模拟

ANSYS/LS-DYNA软件是目前国际上著名的通用显式动力学有限元分析软件,能够模拟各种复杂的结构计算问题,特别适合求解二维、三维非线性结构的高速碰撞、侵彻和爆炸冲击等非线性动力学问题[6]。由于防护工程的特殊性,弹体侵彻危险性很大,会对结构造成严重的破坏,做原型试验难度较大,所以文中应用ANSYS/LS-DYNA程序进行数值模拟研究。

1.1 数值模拟方案

弹体选用小直径炸弹(SDB),该炸弹具有性能优异且方便携带的特点,特别适合现代的反恐作战和近距离交火。现有SDB武器系统由GBU-39小直径炸弹、载弹系统、任务规划系统和后勤支援系统组成。包括弹架和4枚GBU-39/B炸弹在内,整套装置重664 kg,长3.6 m、宽0.40 m、高0.40 m。GBU-39小直径炸弹技术参数见表1。

表1 GBU-39技术参数

注:CRH为弹体头部表面曲率半径与弹体横截面直径之比。

文中选用1枚GBU-39/B炸弹对地下洞室进行垂直侵彻,侵彻点位于拱顶正上方,建模型时将其弹体视为均质实体,形状为卵形弹头。

地下洞室多为直墙拱结构,因此,数值模拟方案的结构形式为直墙拱结构,直墙部分高度为2 m,计算工况如表2所示[7]。

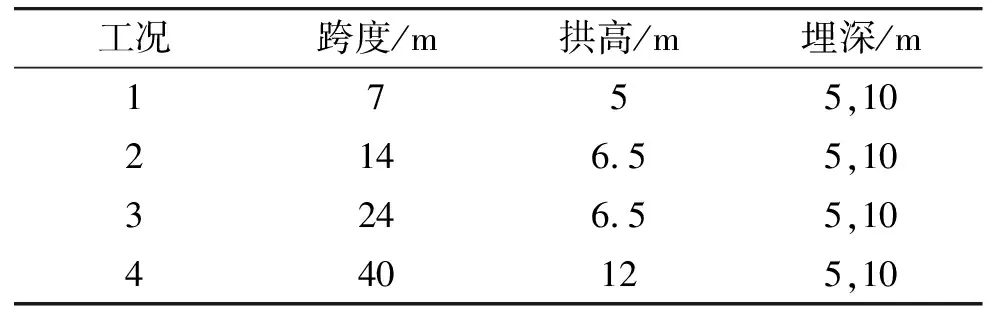
表2 数值模拟方案

1.2 材料模型

弹体选用MAT_JOHNSON_COOK材料模型,在考虑了应力、应变和温度效应的同时,也能够清晰地描述弹体在侵彻过程中的变形和受力特性。

岩石和混凝土拱形被覆结构均选用JOHNSON_HOLMQUIST_CONCRETE材料模型,该模型综合考虑了大应变、高应变率、高压效应,考虑了损伤及损伤积累,材料参数见文献[8]。

1.3 算法选择与计算模型

数值模拟采用Lagrange算法。为简化起见,将岩体宏观上看成连续、各向同性的均质体,不计实际上存在的裂隙影响。由于结构存在大跨度,洞室为细长型,长度方向取10 m、被覆结构两边各取5 m进行数值模拟。为节约计算时间和存储空间,文中仅建立1/4模型,同时在对称面上设置对称面约束,并将无反射边界条件实现于计算模型中[9]。在对洞室进行网格划分时,对弹体与洞室侵彻接触的区域网格进行加密,距离弹靶接触区域较远的地方网格划分较稀疏。图1为计算模型及网格划分情况。

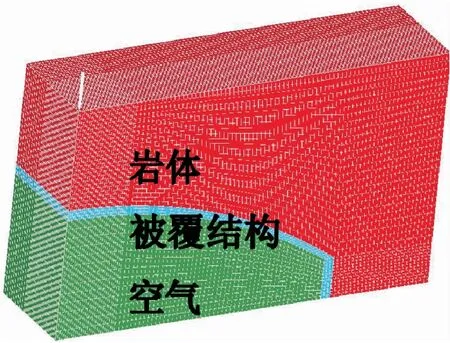
图1 计算模型

2 数值模拟验证

弹体侵彻岩体的机理十分复杂,长期以来此类问题的研究以试验为基础,并根据大量试验数据建立了侵彻深度的计算公式用于工程设计计算[10]。

目前国内外针对岩体介质的侵彻深度计算公式主要有Young公式、Bernard公式、别列赞公式及我国早期拟合公式等7种,文献[11]根据美国桑迪亚国家实验室的试验结果,评价了Young公式预测弹体在低、中强度的岩体中侵彻深度的精度和一致性,认为经验公式预测的侵彻深度与试验数据吻合较好。Young公式如下[12]:

(1)

式中:H为弹体侵彻深度;M为弹体质量;A为弹体横截面面积;v为弹体初始撞击速度;K为缩尺效应系数。

(2)

N为弹头性能系数,对于卵形弹:

(3)

式中:Ln为弹体头部长度;d为弹体直径;S为岩石的可侵彻性指标,S=2.7(YQ)-0.3,其中Y为岩石无侧限抗压强度(MPa),Q为岩石质量指标,取值范围在0.1～1.0之间。

代入相关数据得出,SDB小直径炸弹侵彻花岗岩的深度为1.30 m,数值计算得到的侵彻深度为1.16 m,如图2,与经验公式计算数值相近。验证表明:数值模拟方案选择合理。

图2 数值模拟

从图2可以看出,在9.6 ms时刻之后,弹体停止侵彻,其侵彻深度趋于定值。但之后会出现少量回弹,主要是因为弹体速度为零后,弹坑形成新的自由面,侵彻末端的岩石已无外界能量提供,部分变形逐渐恢复,出现侵彻深度随时间增长有少量回落的现象。

3 动力效应分析

3.1 受力分析

当压缩波从一种材料向另一种材料传播时,会产生反射和透射现象,反射波和透射波的性质主要取决于材料波阻抗ρc的大小。花岗岩的波阻抗为1.40×107kg/(m2·s),大于混凝土的波阻抗0.84×107kg/(m2·s),则应力波由岩石传递至混凝土表面时,将发生卸载反射,透射至混凝土的应力波将减小。当混凝土中的透射波传递至被覆结构下表面时,空气的波阻抗显著小于混凝土的波阻抗,可看作自由面反射,入射压缩波完全被反射为拉伸波。随着弹体侵彻的进行,该过程不断重复发生,被覆结构各部分受压(拉)力反复作用,在达到最终侵彻深度时刻左右受力最大,图3较好地说明了这个过程。从图3还可以看出,拱顶承受的压(拉)力最大,远高于其他部位受力,且拱顶最先受力,拱脚最后受力,这是由波的传播顺序决定的。

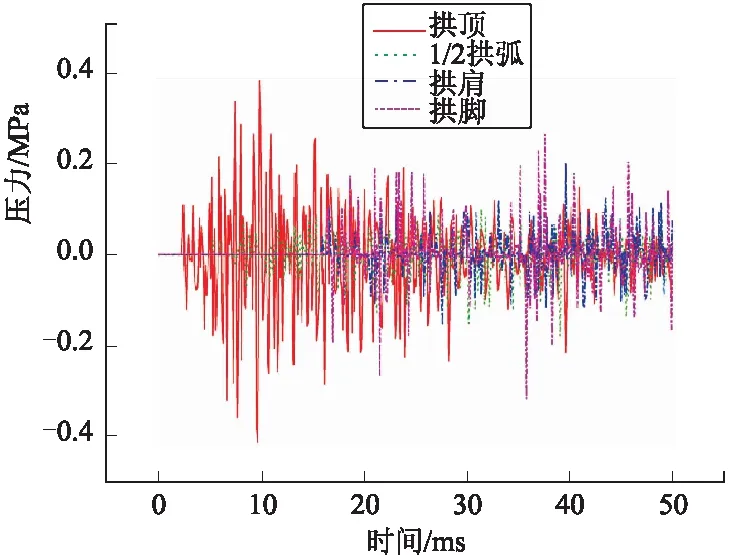
图3 40 m跨度洞室各部分受力情况

根据弹体侵彻不同跨度、不同埋深的洞室数值模拟结果可知,洞室各部分受力随时间不断发生变化,但是所受最大压(拉)力对被覆结构的破坏起控制作用,各种跨度拱不同部位的受力情况见表3。

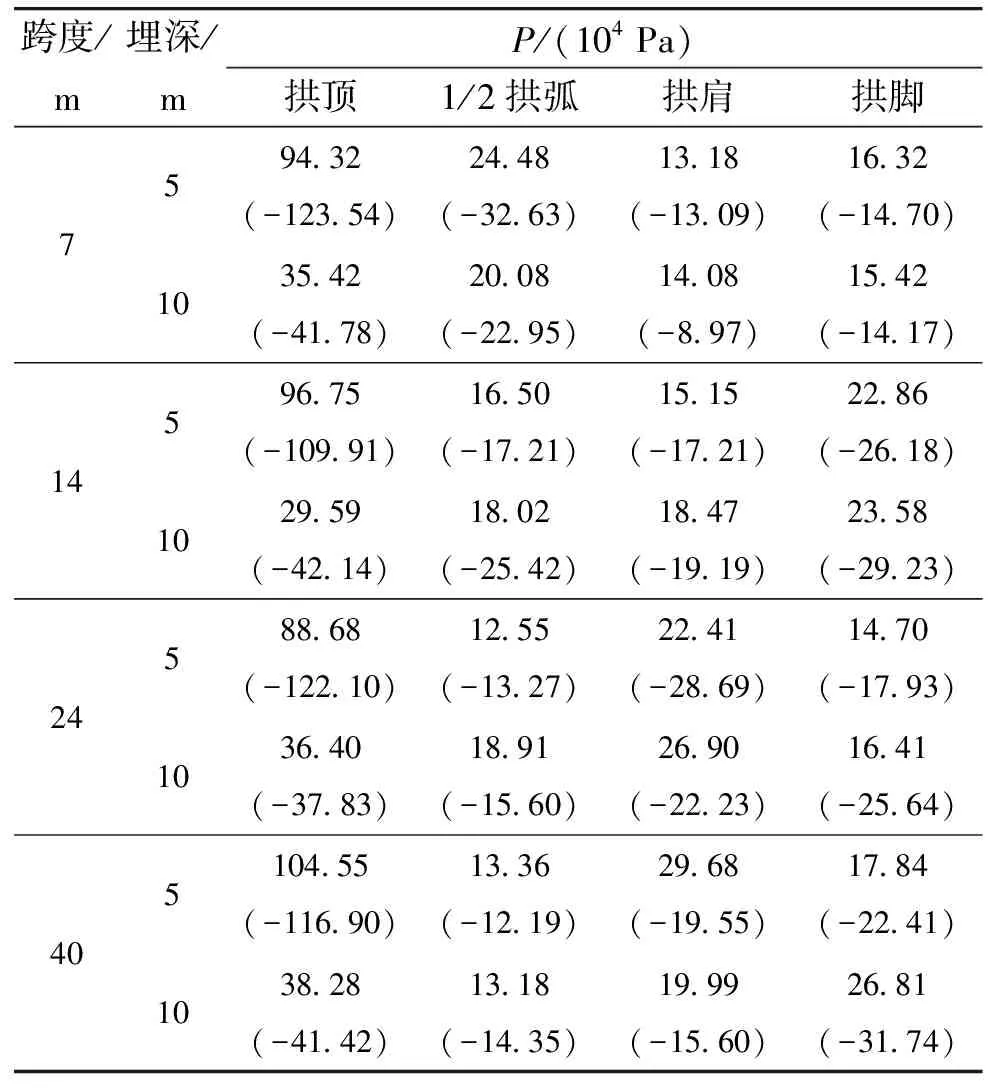
表3 洞室各部分最大压(拉)力

由表3可知,当埋深相同时,不论跨度多大,拱顶处受力最大,由拱顶向拱脚呈减小趋势,且跨度不同时拱顶处所受压力相差较小,表明跨度因素对拱顶受力影响不大;埋深为5 m时,从拱顶处到1/2拱弧处所受压力下降较快,14 m以下跨度洞室拱肩处压力会继续下降,而24 m以上跨度洞室拱肩处所受压力较大,尤其是40 m跨度洞室,拱肩处压力达到了296.77 kPa,远大于1/2拱弧处和拱脚处压力,这是由于围岩竖向变形致使拱肩向外变形受到围岩约束,压力增大。

当埋深不同时,同一部位的受力情况拱顶下降较快,其他部位变化较小甚至受力增大,拱脚处表现较为明显。这是因为埋深增加到10 m时,侵彻荷载作用的范围不再是拱顶局部范围内,而是作用于整个被覆结构;另一方面,由于跨度较大,应力波传至其他部位尤其是拱脚部位时间较长,使得应力波的叠加效应各不相同。

3.2 位移响应

当结构受到侵彻荷载作用时,由于应力波的作用,使得结构各部分产生位移响应。图4和图5分别为5 m埋深时7 m小跨度洞室和40 m大跨度洞室各部分的竖向位移情况。

图4 5 m埋深7 m跨度洞室各部分竖向位移

图5 5 m埋深40 m跨度洞室各部分竖向位移

可以看出,7 m跨度洞室各部分竖向位移基本相同,拱顶位移曲线波动相对剧烈。40 m跨度洞室各部分竖向位移差别较大,拱顶和1/2拱弧位移竖直向下,拱顶受力后立即向下运动,而1/2拱弧在7.5 ms后才开始向下运动,两处位移下降幅度基本相同,拱顶下降速率先快后慢,1/2拱弧下降速率先慢后快;拱肩和拱脚位移竖直向上,基本同时运动,是因为洞室跨度较大,而直墙高度较小,应力波由拱顶传播至拱肩所需时间是由拱肩传播至拱脚所需时间的10倍,且拱肩和拱脚处于同一垂直面上,使得该两处位移响应相同。

图6为10 m埋深时40 m大跨度洞室各部分的水平位移情况,可以看出,拱顶水平方向较为稳定,基本不产生运动,随着与拱顶距离越远,结构的振幅越大,拱脚的位移响应最为剧烈。在17 ms至27 ms时间内,拱肩和拱脚部位水平位移迅速增大,随后缓慢增长至45 ms再减小,而1/2拱弧水平位移在0 ms至50 ms时间内增长都比较缓慢。

图7为10 m埋深时不同跨度洞室拱脚处的水平位移,可以看出,跨度越大,拱脚处开始振动的时间越晚,水平位移越大,位移响应越剧烈。且随着跨度增大,振动周期逐渐增加,7 m跨度为24 ms,14 m跨度为50 ms,24 m跨度为80 ms,40 m跨度为100 ms。

图6 10 m埋深40 m跨度洞室各部分水平位移

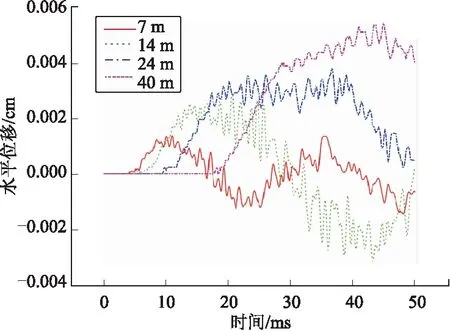
图7 10 m埋深洞室拱脚处水平位移

4 结论

通过对弹体侵彻作用下不同跨度地下洞室的数值分析,可以得到以下结论:

1)选用Young公式计算侵彻岩石的深度,与数值模拟结果相比较,基本一致,表明数值模拟方案合理,也说明该公式在预估弹体侵彻岩石深度方面使用的普遍性。

2)当地下洞室埋深为5 m时,拱顶处受力最大,14 m以下小跨度洞室拱脚部位受力较大,24 m以上大跨度洞室由于围岩的约束作用会使得拱肩部位受力较大;当地下洞室埋深为10 m时,被覆结构不再是拱顶范围局部受力,而是荷载作用于整个被覆结构,且由于应力波的叠加效应,使得拱脚部位受力较大。

3)小跨度洞室各部分竖向位移基本相同,大跨度洞室拱顶和1/2拱弧向下运动,拱肩和拱脚向上运动;不同跨度洞室各部分水平位移拱脚最大,且随着跨度增大,拱脚水平位移增大。

参考文献:

[1] 任辉启, 穆朝民, 刘瑞朝, 等. 精确制导武器侵彻效应与工程防护 [M]. 北京: 科学出版社, 2016: 1-11.

[2] GOLD V M. Analysis of the penetration resistance of concrete: AD-A329 140[R]. [S.l.:s.n.], 2000.

[3] WARREN T L, FOSSUMA F, FREW D J. Penetration into low-strength (23 MPa) concrete: target characterization and simulations [J]. International Journal of Impact Engineering, 2004, 30(5): 447-503.

[4] 郑振华, 余文力, 王涛. 钻地弹侵彻高强度混凝土靶的数值模拟 [J]. 弹箭与制导学报, 2008, 28(3): 143-146.

[5] 徐干成, 顾金才, 张向阳, 等. 地下洞库围岩外加固抗炸弹侵彻性能研究 [J]. 岩石力学与工程学报, 2012, 31(10): 2064-2070.

[6] 石少卿, 康建功, 汪敏, 等. ANSYS/LS-DYNA在爆炸与冲击领域内的工程应用 [M]. 北京: 中国建筑工业出版社, 2011: 82-88.

[7] 孙惠香, 许金余, 朱国富, 等. 爆炸作用下跨度对地下结构破坏形态的影响 [J]. 空军工程大学学报, 2013, 14(2): 90-94.

[8] 沈俊, 刘瑞朝, 杨建超, 等. 弹体侵彻岩体效应试验与理论研究 [J]. 岩石力学与工程学报, 2008, 27(5): 946-952.

[9] 孙惠香, 许金余, 李庆. 爆炸荷载作用下地下结构破坏模式研究 [J]. 弹箭与制导学报, 2011, 31(5): 89-92.

[10] 吴祥云. 细长弹侵彻防护工程材料靶体的试验和理论研究 [D]. 长沙: 国防科学技术大学, 2002.

[11] PATTERSON W, BATY R S. 两个经验公式与现场试验结果的比较 [C]∥第十一届武器效应与结构相互作用国际专题讨论会文集. 洛阳：总参工程兵科研三所, 2003: 465-468.

[12] 张德志, 林俊德, 唐润棣, 等. 高强度岩石侵彻经验公式 [J]. 兵工学报, 2006, 27(1): 15-18.