基于仿射变换的有理函数模型精化研究

巩丹超，张 丽，龚 辉

1.西安测绘研究所，陕西 西安，710054;

2.地理信息工程国家重点实验室，陕西 西安，710054

1 引 言

作为一种通用的传感器几何模型，有理函数模型(rational function model，RFM)已经成为光学遥感卫星几何模型的标准形式。已有的研究表明，无控制点条件下利用严格传感器模型生成的有理函数模型带有一定的系统误差[1-4]，因此，在实际大区域数据处理应用中，需要通过区域网平差的方式，消除系统误差，提高影像的整体定位精度。目前常用的区域网平差原理是将仿射变换应用于有理函数模型，采用像方补偿方案通过最小二乘平差求解仿射变换系数。这样，平差后每一景影像的定向参数除了有理函数模型系数，又新增了6个仿射变换系数。目前，部分商业软件不支持有理函数模型附加的仿射变换定向参数。因此，本文针对“天绘一号”卫星影像，在区域网平差的基础上，结合获得的仿射变换参数和原有理函数模型系数，按照严格模型拟合有理函数模型的方法，重新拟合生成了一套新的有理函数模型系数，并通过实验验证了本文提出方法的正确性和可行性。

2 有理函数模型区域网平差基本原理

有理函数模型是严密几何成像模型的高精度拟合，已有研究表明RFM参数常包含误差。将仿射变换模型应用于有理函数模型进行区域网平差，与基于共线方程的光束法空中三角测量的思想是一致的。即以一幅影像所组成的一束光线作为平差的基本单元，以有理函数模型组合仿射变换作为平差的基础方程;通过各个光线束在空间的旋转和平移，使模型之间的公共点的光线实现最佳交会，并使整个区域最佳地纳入到已知的控制点坐标系统中去。采用基于像方补偿方案能够很好地消除其对影像几何定位结果的影响，常用的带仿射变换的像方补偿RFM如式(1)所示：

式中，(Xn，Yn，Zn，rn，cn) 为物方和像方的归一化坐标;p1、p2、p3、p4为有理多项式;(a0，a1，a2，b0，b1，b2)是影像的6个仿射变换系数。其中，平差参数a0将吸收扫描方向上位置和姿态误差所引起的影像列方向上的误差;平差参数b0将吸收飞行方向上位置和姿态误差所引起的影像行方向上的误差，由于影像的行一般对应于星载传感器的飞行方向，影像的行与每条CCD线阵的瞬时成像时间相关;平差参数b1和a2将吸收由星载GPS和惯性导航系统漂移误差所引起的影像误差;而参数a1和b2则吸收因内定向参数误差所引起的影像误差[5]。

3 基于仿射变换的有理函数模型精化

通过区域网平差可以提高影像的整体定位精度，但在传统有理函数模型系数的基础上，又新增了6个系数，这样实际应用中影响了有理函数模型的通用性和标准化，对后续数据处理带来不便。因此，本文将已有的有理函数模型系数和仿射变换系数相结合，借鉴严格模型生成有理函数模型的方法，重新生成一组新的有理函数模型。具体的思路是：首先构建覆盖成像区域的层状虚拟格网(包括检查点和控制点格网)，格网点在像方空间均匀分布于整景影像，在物方的高程方向上以若干层均匀分布，其中高程的取值范围与实际的地形起伏基本一致;其次根据格网点的像方坐标和高程值，利用已有的有理函数模型和平差后仿射变换系数，计算出物方坐标的经度和纬度;然后利用控制点格网作为观测值，按照最小二乘平差的方法求解一组新的RFM系数;最后利用检查点格网数据，对新生成的RFM系数进行精度分析和评估。

3.1 层状虚拟格网点的生成

层状虚拟格网点的生成包括以下3个步骤：

(1)将整幅影像均匀分成m×n个网格，通常m、n取相同的值。当m=n=10时，在整幅影像上有11×11=121个均匀分布的像点。

(2)把影像覆盖区域的高程范围(hmin～hmax)均匀分为k层(为避免法方程出现病态，一般k＞3)，每层具有相同的高程Z，并都有上述(m+1)×(n+1)个均匀分布的像点。这样就产生(m+1)×(n+1)×k个在平面、高程上均匀分布的格网点，并且每个格网点的像点坐标(r，c)及高程Z均已知。

(3)用影像已有的有理函数模型系数和整体平差后的仿射变换系数，根据每个格网点的像坐标(r，c)和高程H计算出物方坐标(L，B)，这样就得到(m+1)×(n+1)×k个格网点的全部坐标。最后生成的层状格网点分布如图1所示。其中控制点和检查点格网生成方法一致，检查点与控制点的像方位置整体之间有偏移，偏移距离通常为像方网格间距的一半。

图1 虚拟层状格网示意图

3.2 RFM系数的解算

采用最小二乘原理求解RFM的系数，需要将传统有理函数模型线性化，从而得到下述误差方程式：

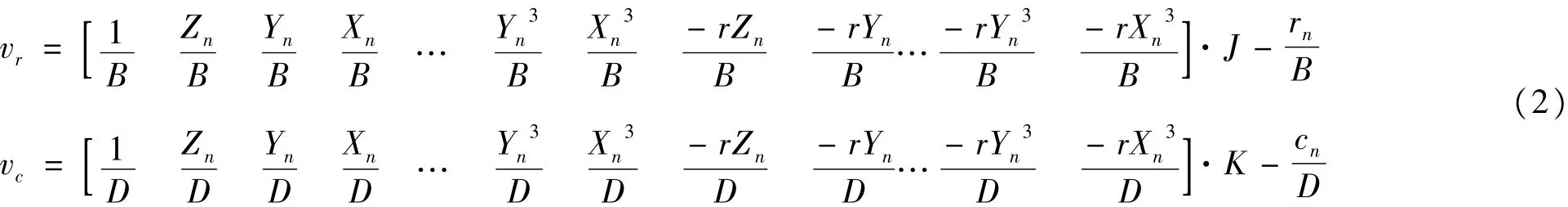
这里，

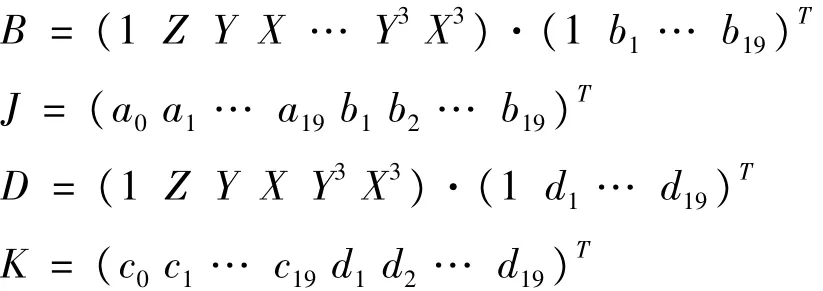
其中，(Xn，Yn，Zn，rn，cn) 为物方和像方的归一化坐标;为多项式的系数。根据上述误差方程，就可以实现RFM系数的解算。

3.3 精度检查

用解算出来RFM的系数计算这些格网检查点的地面位置或相应像点的位置。通过比较解算的坐标和已知的格网点坐标，然后进行统计就可以得到区域网平差的精度。

4 实验及结论

4.1 实验数据

本文采用“天绘一号”02星的1B级影像产品作为实验数据，数据包含卫星影像和对应的RFM参数以及区域网平差后的仿射变换系数。实验区域位于齐齐哈尔市西北，该测区共有相邻2条带数据，每条带2景数据，共含有4景前视、下视、后视全色影像，总共12张影像。影像质量良好，区域内高差大约300m。平差采用商用软件ERDAS IMAGINE完成，有26个GPS测量控制点，选择6个作为控制点，20个作为检查点。图2是4景影像中的下视影像。

图2 天绘一号影像(4景下视)

4.2 实验方法

在对上述4景影像进行有控区域网平差的基础上，按文中方法用平差结果构建虚拟层状控制点格网(平面格网分布10×10，高程分层为10层，共计1000个点)，利用格网点坐标，解算出一组新RFM系数;然后按照类似于虚拟层状控制点格网的生成方法生成检查点虚拟层状格网，将检查点利用新RFM计算的像点坐标，与已有RFM附加平差后仿射变换系数计算的像点坐标相比较，可以得出这一过程的内部拟合精度;另外，利用实际控制点作为检查点，对比分析新RFM与已有RFM附加仿射变换系数的精度，包括内部拟合精度和外部定位精度。对每一张影像，利用检查点的物方坐标计算出像方坐标，然后计算实际量测坐标与计算的像方坐标的差值，统计全部影像的所有点结果取均方根即内部拟合精度;对每一个检查点，利用其在对应影像上的像方坐标通过三视立体进行前方交会计算出物方坐标，然后计算实际量测坐标与解算的物方坐标差值，统计所有的结果取均方根即外部定位精度。具体实验过程如图3所示。

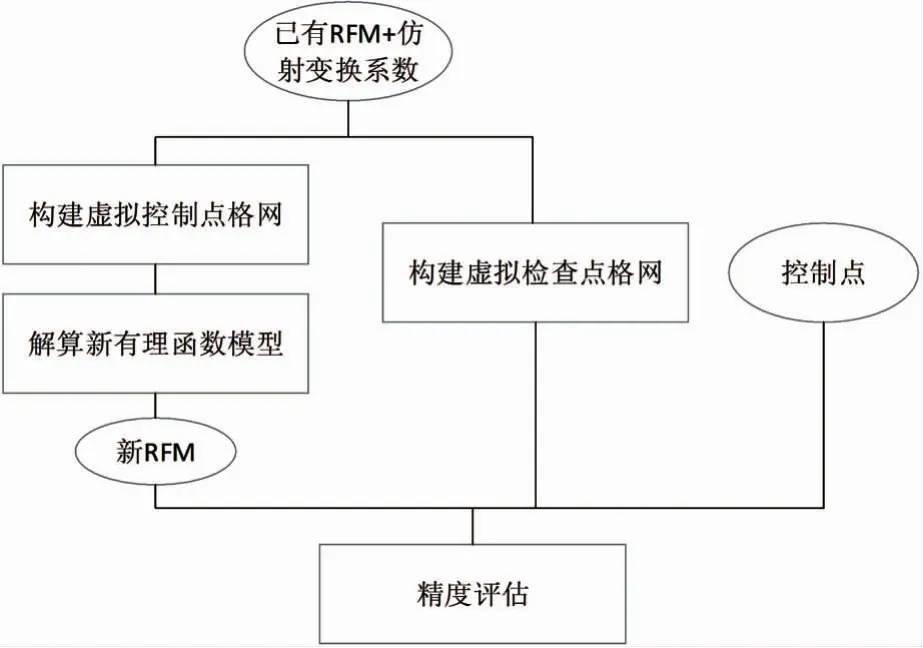
图3 实验过程

4.3 实验结果

表1列出了其中两景影像平差结果的仿射变换系数，表2列出两景影像拟合后的内部精度结果对比，表3是利用实际20个检查点对4景影像RFM精化前后外部精度的对比统计结果。

4.4 分析和结论

从表2内部符合情况来看，检查点的拟合精度可以达到10-4像素，拟合误差基本忽略不计;从表3外部精度结果来看，利用实际的检查点，发现精化后的仿射变换附加RFM的定位模型与重新构建的RFM模型精度基本一致，也进一步验证了该拟合过程基本不引入误差。另外，对比“天绘一号”无控定位的相关文献[6]，可以看出，在有控制点条件下“天绘一号”影像平差结果X方向与Y方向精度有较大差异，X方向较好，Y方向较差，而Z方向也有显著提高。初步分析主要原因是X方向为线阵CCD排列方向，是严格中心投影关系;Y方向为卫星飞行方向，是多中心投影或者近似平行投影的关系。

表1 两景影像区域网平差的结果(仿射变换系数)

表2 两景影像精化后的内部拟合精度

表3 RFM精化前后外部定位精度对比

通过上述分析可以得出，对于“天绘一号”卫星影像，经过区域网平差后生成一组新的有理函数模型参数，是完全可以替代原先的复合式定向参数(即有理函数模型系数和仿射变换系数)。

5 结束语

本文针对“天绘一号”光学卫星影像基于仿射变换的区域网平差结果，借鉴严格几何模型拟合有理函数模型的方法，将平差结果重新拟合形成一套新的有理函数模型，以实现对已有的有理函数模型精化。实验结果验证了该方法的正确性和可行性，也进一步说明了有理函数良好的拟合特性。通过精化处理，可以简化定向参数的形式，这样符合有理函数模型建立和应用的初衷：通用性和标准化，对后续的处理应用提供便利。

[1]Xinghe Yang.Accuaracy of Rational Function Approximation in Photogrammetry[C].Washington：Proceedings of2000 ASPRSAnnual Convention，2000.

[2]C.VicentTao，Yonghu.Investigation on the Rational Function Model 2000[C].Washington：Proceedings of 2000 ASPRSAnnual Convention，2000.

[3]C.VicentTao，Yonghu.A Comprehensive Study of the Rational Function Model for Photogrammetry Processing[J].PE&RS， 2001 67(12)：1347-1357.

[4]GRODECKIJ，DIALG.Block Adjustment of High Resolution Satellite Images Described by Rational Polynomials[J].Photogrammetric Engineering and Remote Sensing，2003，69(1)：59 68.

[5]张力，张继贤，陈向阳等.基于有理多项式模型 RFM的稀少控制SPOT5卫星影像区域网平差[J].测绘学报，2009，38(4)：302-309.

[6]王任享，王建荣，胡莘.光学卫星摄影无控定位精度分析[J].测绘学报，2017，46，(3)：332-337.