海洋重力测量中低通滤波器的设计与应用

韦建成，肖 云，王 利，孟 宁，邹嘉盛

1.长安大学地质工程与测绘学院，陕西 西安，710054;

2.地理信息工程国家重点实验室，陕西 西安，710054;

3.西安测绘研究所，陕西 西安，710054

1 引 言

海洋重力测量是在运动状态下实施重力测量，受到海浪起伏、航速变化、仪器振动以及海风和海流等因素的影响，观测值中不可避免地含有很多测量误差。重力观测值会受到水平加速度、垂直加速度、测量船转弯、交叉耦合以及Eötvös效应等多项干扰加速度的影响，一些干扰项的量级往往比实际重力加速度的量级大得多，为了得到高精度重力测量结果，必须从重力观测值中剔除这些干扰项的影响，最大程度地还原真实的重力异常信号。

对于消除重力测量误差，可以从硬件和软件两方面入手。在硬件方面，通过增加合适的阻尼系统，消除垂直方向上干扰加速度对重力观测值的影响。在软件方面，可以通过设计合理的数字滤波器，对重力测量信号进行滤波，剔除高频噪声，最大程度上还原真实重力信号。相比于增加仪器阻尼的方法，采用数字滤波器的方法更易实现。在硬件改进无法满足要求时，可以采用滤波的方法来提高测量精度。目前应用于海洋重力测量数据处理的滤波器种类繁多，主要有RC(Resistor-Capacitor)滤波器、FIR(Finite Impulse Response)滤波器和IIR(Infinite Impulse Response)滤波器等。RC滤波器存在相位延迟，导致其灵敏度较低;IIR滤波器的典型代表巴特沃斯(Butterworth)低通滤波器也在一些海洋重力测量实践中得到成功应用，但这种滤波器不具有线性相位，不能保证滤波前后波形的一致性，并且还存在潜在的不稳定性;FIR滤波器的优点是具有精确的线性相位而且系统总是稳定的。海洋重力测量中采集数据的传感器众多，数据处理中就需要保持滤波前后数据的形状相一致，这就要求所设计的滤波器具有精确线性相位，FIR滤波器特性满足此要求。第二代L&R海空重力仪已经开始使用Blackman滤波器(属于FIR滤波器)替代传统的RC滤波器。此外，测量数据中不可避免地含有粗差，若粗差未能完全剔除，则递归运算中的粗差累积影响势必比非递归运算大，因此，FIR滤波器输出结果较IIR滤波器更加稳定[1～3]。窗函数法设计的滤波器应用于海洋重力数据处理的文献相对较多，并且这种方法在实际应用中也取得了很好的效果，详见文献[1]。基于最佳一致逼近法设计的滤波器在航空重力测量中得到了成功的应用，但在海洋重力测量数据处理方面还未见有相关文献;频率采样法设计的滤波器在海洋重力测量数据处理中也少有应用。所以，本文着重讨论后两种FIR数字滤波器在海洋重力测量数据处理中的设计与应用。

本文基于最佳一致逼近法和频率采样法设计了两种FIR数字低通滤波器，并以窗函数滤波器结果为依据，采用模拟数据来验证滤波器的性能。对海洋重力实测数据进行了滤波处理，详细对比了两种滤波器的效果。

2 数据模型

2.1 海洋标量重力测量

海洋重力测量的基本模型为：

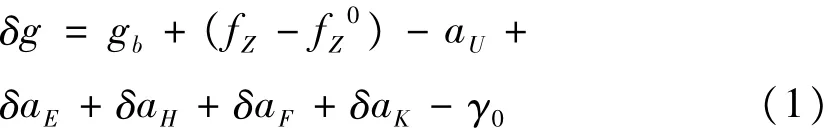
式中，δg为测点重力扰动;gb代表码头处的重力值，由陆地重力仪从重力基点联测得到;fZ、fZ0为比力观测值及其初值;aU为载体垂直加速度改正;δaE为厄特弗斯改正;δaH为水平加速度改正;δaF为空间改正;δaK为零点漂移改正;γ0为椭球面上的正常重力。以上各项改正中均含有高频误差，需要进行滤波处理。

2.2 FIR低通滤波算法

FIR滤波可以表示为一个差分方程：

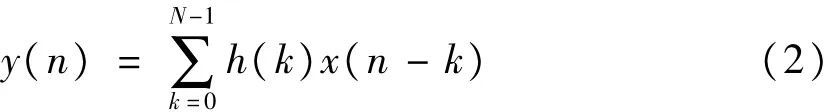
式中，x(n)是输入信号;y(n)是滤波后输出信号;h(k)是滤波器系数;N是滤波器的长度。因而，滤波的关键在于如何求解出合适的滤波器系数。

2.2.1 窗函数法

窗函数法的设计思想是用一个有限时宽的h(n)逼近理想的低通滤波器的脉冲响应hd(n)，使其频率响应H(ejω)逼近理想低通滤波器的频率响应Hd(ejω)。窗函数法设计过程中，h(n)和hd(n)的关系可以表示为：

式中，w(n)为窗函数。由于Hanning窗具有较快的衰减速度，选择Hanning窗来设计滤波器，实际编程中令主瓣宽度的一半等于实际的归一化截止频率来估算滤波器长度。Hanning窗的具体参数可查阅相关信号处理书籍。

2.2.2 最佳一致逼近法

最佳一致逼近法也称为Chebyshev(切比雪夫)逼近法，是在所关注的频段内使误差函数

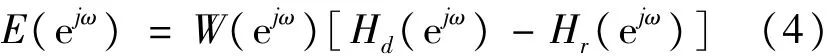
较为均匀一致，通过选择合适的H(ejω)和权函数W(ejω)，使 E(ejω) 的值达到最小。权函数可通过下式进行构造

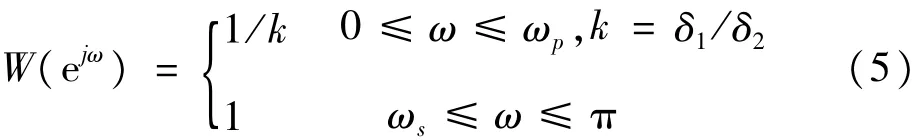
式中，ωP是通带截止频率;ωs是阻带截止频率;δ1是通带波纹峰值;δ2为阻带波纹峰值，它们可通过通带最大衰减Ap、阻带最小衰减As换算得到，具体换算关系可参考文献[4]。实际编程中可利用Remez交换算法迭代求解出滤波器系数。

2.2.3 频率采样法

频率采样法是从频域出发，在频域直接设计。首先根据频域的采样定理，以等频率间隔对Hd(ejω) 取样得到 H(k)：

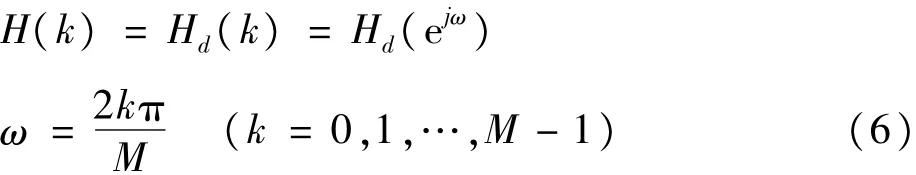
式中，H(k)为理想低通滤波器的冲击响应，其他符号意义同前。

然后由H(k)通过离散傅里叶逆变换(Inverse Discrete Fourier Transform，IDFT)得到滤波器序列h(n)：

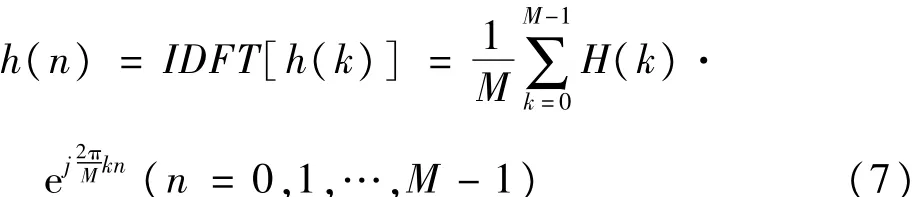
3 算例分析

3.1 垂直加速度模拟及滤波器参数设置

对于垂直干扰加速度，由波浪运动所引起的测量船垂直方向加速度的周期一般为5～10s，且以6s居多，相对于变化缓慢的重力值来说，该干扰信号属于高频扰动。船舶运动造成的能量大多集中于1/20～1/3Hz的频率范围内，而重力异常的频率一般小于1/120Hz。海况平静时海浪产生的垂直加速度在15Gal，恶劣时达到300Gal[5]。

假设海浪引起的垂直加速度信号的幅值为10mGal，频率分布在处;垂直干扰加速度信号由3个高频信号叠加合成，其幅值为50Gal，频率为z，则量测加速度信号为：(采样频率Fs为1Hz)

垂直扰动加速度信号为：

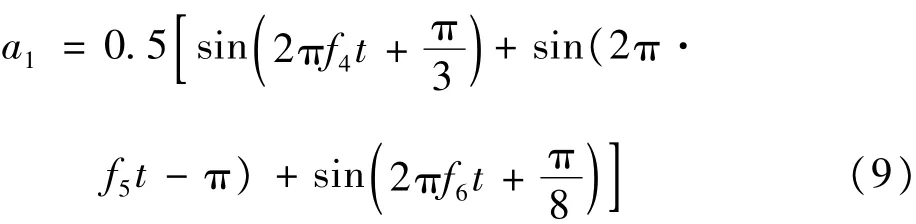
为了检测滤波器在消除垂向高频扰动加速度的效果，通过MATLAB软件进行仿真。滤波过程中还存在相位延迟，为此文中采取先将数据按顺序滤波，然后将所得结果逆转后再反向滤波的策略，这样就可实现零相位滤波。为便于后文陈述，这里把采用Hanning窗、最佳一致逼近法和频率采样法设计的FIR低通数字滤波器分别称为滤波器1、滤波器2和滤波器3，图1给出了这三种滤波器的实际脉冲响应和幅频特性曲线，三种滤波器对应的滤波器长度N分别为267、221、259阶。从图中可直观看出，三种滤波器在通带具有较好的低通性能，在阻带具有较大的衰减，能够抑制窗口以外的信号。

3.2 滤波器性能检测

为了对比滤波器对弱随机噪声和高频扰动噪声的滤波效果，本文采取两种方案对3.1节模拟的加速度信号进行滤波处理。方案一：在量测信号的基础上添加0.5倍幅值大小的随机噪声，然后对信号进行滤波处理;方案二：在量测信号的基础上添加高频扰动噪声，然后对信号进行滤波处理。两种方案的信号时域波形如图2所示。

图1 三种FIR低通滤波器的脉冲响应和幅频响应

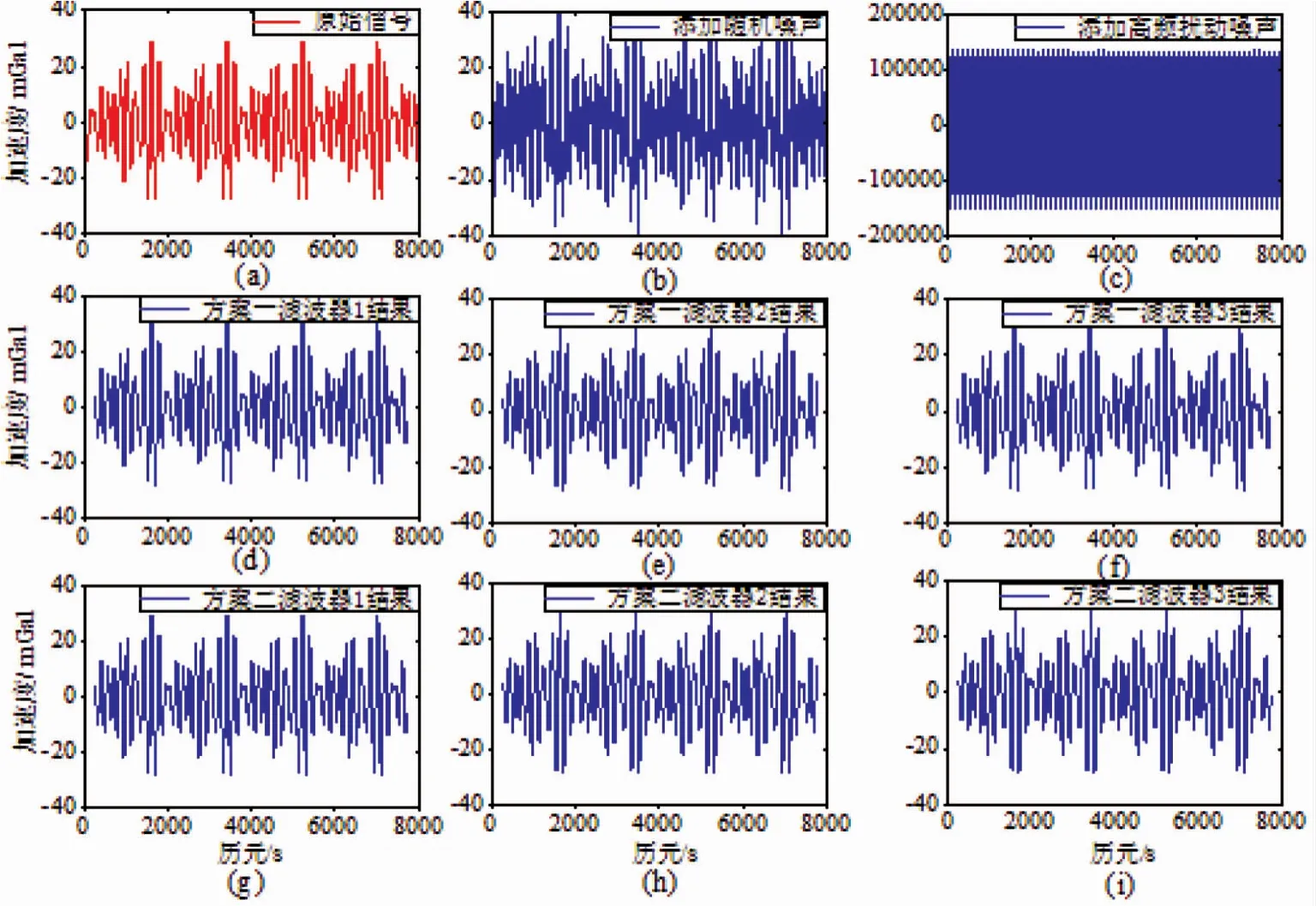
图2 两种方案的信号时域波形

由于滤波过程还存在边界效应，需要对数据进行截断。本文以滤波器长度N为截断长度在滤波后数据的端部进行截断处理，其起始端点比量测加速度序列的端点落后N个历元，同时相应的序列长度比量测加速度序列短2N个历元[6]。

为了比较滤波后加速度信号与量测加速度信号的差异，以量测加速度信号为参考值，在滤波值与参考值之间求差。以窗函数滤波器结果为依据，对采用最佳一致逼近法和频率采样法设计的滤波器进行对比。对图2中信号的精度进行了统计，其结果见表1。方案一所得结果见图3和表2。方案一结果显示，采用Hanning窗、最佳一致逼近法和频率采样法设计的低通滤波器所得加速度序列精度分别为 0.777mGal、0.841mGal和0.914mGal，滤波器2的效果略好于滤波器3，这说明本文设计的两种低通滤波器能够从含有弱随机噪声的加速度信号中提取出原始加速度信号。

表1 两种方案加速度统计结果

表2 方案一滤波后加速度与参考值之差的相关统计信息

图3 方案一信号截断后所得滤波值与参考值的差

图4描述了高频扰动噪声信号经三种滤波器滤波后所得结果相对于参考值的变化情况，表3给出了相关统计信息。由表3可知，滤波器2的结果也稍好于滤波器3，这与表2得出结论一致。由于基于最佳一致逼近法比采用频率采样法设计滤波器更容易实现，并且其精度较高，因而最佳一致逼近法设计的低通滤波器在航空重力测量中得到了广泛的应用。滤波器1在方案一和方案二中都表现出了最好的结果，源于其较快的衰减速度。这说明本文设计的低通数字滤波器，质量令人满意能够从含有高频扰动噪声的信号中还原真实信号。

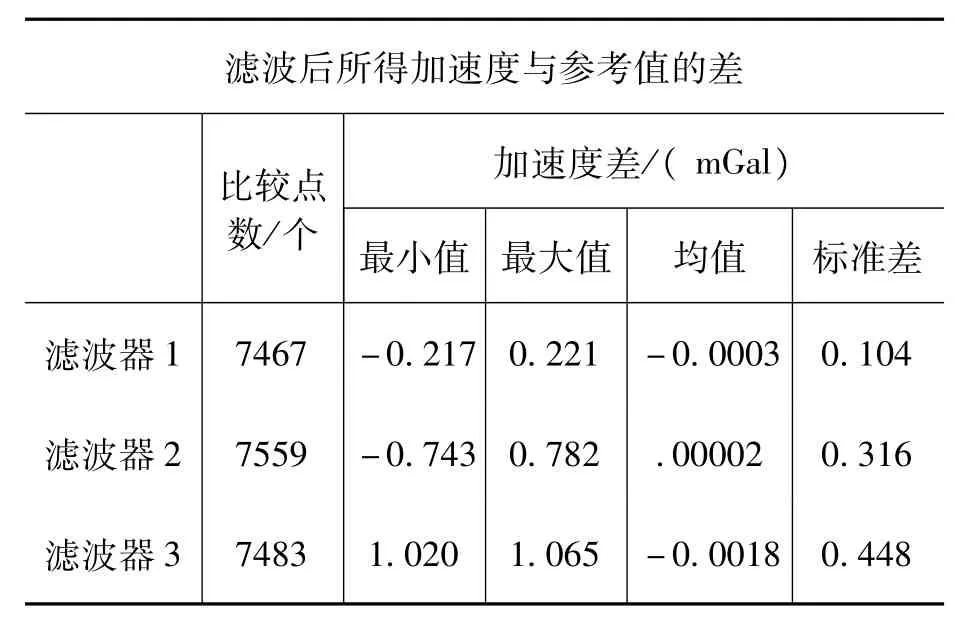
表3 方案二滤波后加速度与参考值之差的相关统计信息

为进一步分析在实际海洋重力测量数据中的应用效果，采集了捷联式船载重力仪在停泊状态的下的重力观测数据，假设重力异常值不改变，则滤波后重力异常残差为实际的重力异常误差。图5给出了三种滤波器的滤波结果，为了对比的公正性，对相同时间段的滤波结果进行了统计，结果见表4。

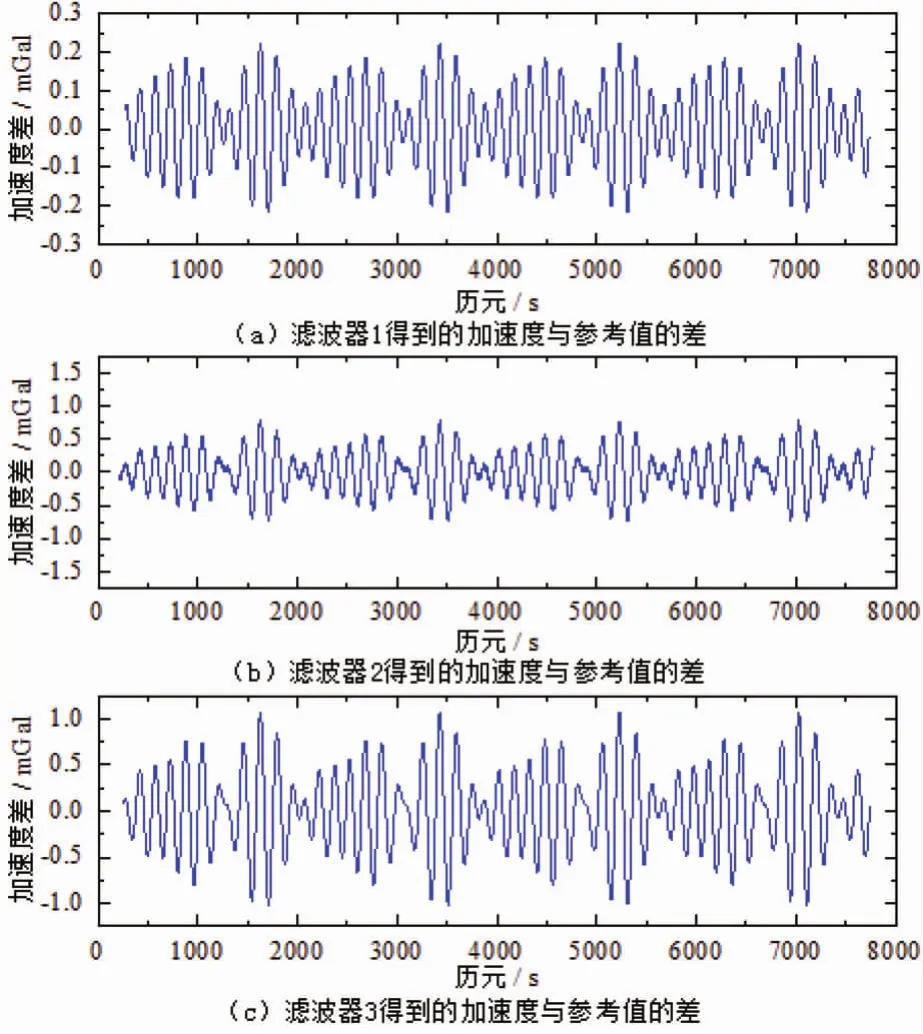
图4 方案二信号截断后所得滤波值与参考值的差

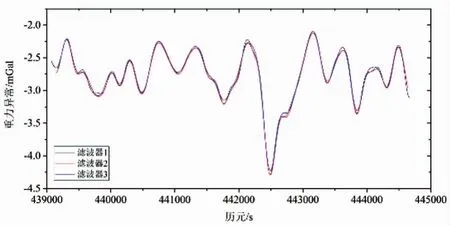
图5 滤波后的重力异常

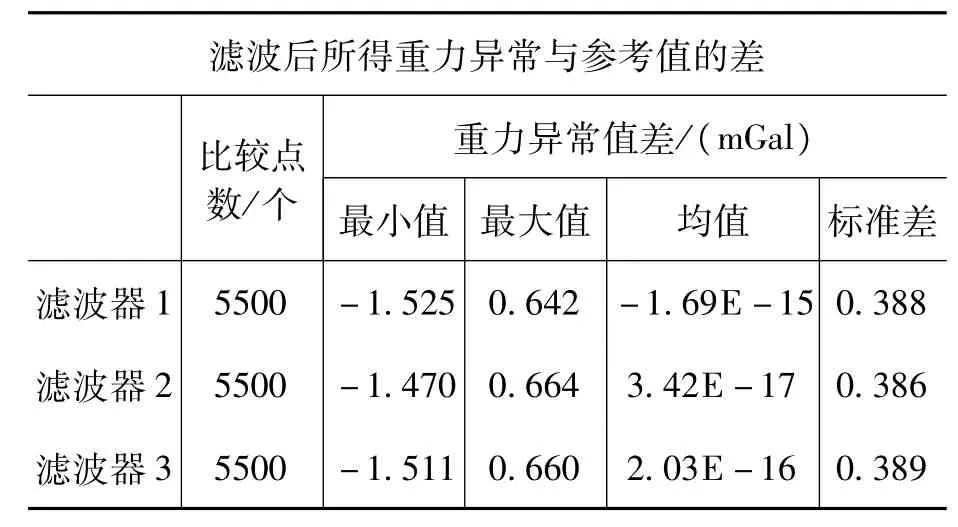
表4 滤波后重力异常与参考值之差的相关统计信息

从表4可看出，滤波器1、2、3的滤波结果的标准差分别为 0.388mGal、0.386mGal、0.389mGal，标准差都在1mGal以内。滤波器2和滤波器3的结果与滤波器1结果吻合较好，这说明本文设计的两种低通滤波器可以将高频扰动噪声分离出来，对滤波后的时间序列进行边界效应改正后可以提取出高精度的重力异常信息。

4 结 语

海洋重力测量数据处理中，由于高频扰动噪声的存在，需要从重力观测数据中还原出真实重力值，低通滤波就显得尤为重要。基于此，本文设计了两种适用于海洋重力测量的FIR低通数字滤波器。以普遍应用的窗函数法设计的滤波器为依据，通过仿真分析，验证了最佳一致逼近法和频率采样法设计的滤波器的性能，结果表明本文设计的两种滤波器具有较好的低通滤波性能。对船载实测重力数据滤波后，两种滤波器都能达到和窗函数滤波器相近的精度;同时发现在相同设计指标下，基于最佳一致逼近法设计的滤波器低通滤波性能略优于采用频率采样法设计的滤波器，而且在达到相近的滤波效果时，基于最佳一致逼近法设计的滤波器所需的长度要小于采用频率采样法设计的滤波器的长度，在数据截短时会保留更多的有效观测信息。当测线上数据量不是很多时，采用最佳一致逼近法设计的滤波器要比基于频率采样法设计的滤波器更优。

[1]欧阳永忠.海空重力测量数据处理关键技术研究[J].测绘学报，2014，43(4)：435-435.

[2]孙中苗，夏哲仁.FIR低通差分器的设计及其在航空重力测量中的应用[J].地球物理学报，2000，43(6)：850-855.

[3]王静波.航空重力测量数据处理方法技术研究[D].北京：中国地质大学，2010.

[4]楼顺天，李博菡.基于 MATLAB的系统分析与设计——信号处理[M].西安：西安电子科技大学出版社，1998.

[5]刘凤鸣.海洋重力测量数据实时处理技术研究[D].哈尔滨：哈尔滨工程大学，2008.

[6]周波阳，罗志才，宁津生等.航空矢量重力测量中有限冲激响应低通数字滤波器的设计[J].武汉大学学报·信息科学版，2015，40(6)：772-778.