低成本高精度GNSS PPK在无人机上的应用

杨 光，龚志辉，蓝朝桢，金庆雄，谢丽敏

信息工程大学地理空间信息学院，河南 郑州，450001

1 引 言

目前，全球导航卫星系统(GNSS)的定位精度已经达到厘米级，差分定位技术被广泛应用于高精度定位中[1]。但是包括基准站和移动站在内的一整套差分GNSS系统不仅价格昂贵而且体积、质量大，在很多领域的应用受到限制。大多数微小型无人机由于载荷限制，通常不能搭载测量级GNSS设备，为了降低硬件成本只搭载轻型单频GNSS接收机。利用这种单频接收机单点定位的误差在10m以上，而且考虑到飞机飞行速度大，定位精度进一步下降。

单频GNSS接收机较之双频定位性能差，主要是因为电离层延时误差所引起[2]。但是在短基线(30km内)的情况下，这种误差影响不大。微小型无人机作业范围通常不超过30km，因此，单频接收机完全可以实现高精度的定位。国内外学者利用这种单频接收机进行了大量试验，在良好的试验条件下，已经达到厘米级静态定位精度，但是稳定性很差[3，4]。鉴于此，本文提出一种融合BDS/GPS的定位算法，实现单频GNSS接收机稳定和高精度定位。若将无人机载移动站和地面基准站记录的原始观测数据进行离线动态后处理(post processing kinematic，PPK)解算，将为无人机提供更加精准的位置信息，尤其是在航空摄影测量中，能够为空中三角测量提供更高精度的外方位元素初始值，在定位精度足够高的情况下，将会极大减少地面控制点的数量，甚至可以实现直接地理定位。

2 差分GNSS测量原理

PPK技术是一种与RTK相对应的定位技术，这是一种利用载波相位观测值进行事后处理的动态相对定位技术[5]。

PPK和RTK测量原理相同，都是利用基准站接收机的测量误差来校正移动站接收机对同一卫星的观测值，从而提高移动站接收机的测量和定位精度。不同之处在于，PPK采用事后处理，这样就避免了差分信号在传输过程中由于遮挡、干扰等因素造成的数据丢失现象。同时差分解算需要一定的计算时间，当无人机等移动载体运动速度过快时会影响定位精度。

载波相位观测方程式：

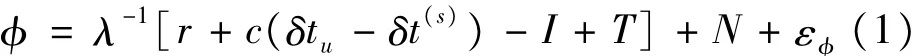
式中，I为载波相位测量值;λ为波长;N为整周模糊度;εφ为载波相位测量噪声量。

如图1所示，利用进行同步观测的基准站接收机和流动站接收机记录卫星的载波相位观测量，事后在计算机中利用GNSS处理算法进行线性组合，形成虚拟的载波相位观测量值，确定接收机之间厘米级的相对位置。

本文研究主要针对低成本GNSS接收机芯片记录的载波相位观测值，进行分析、解算，并提出一种全新的组合算法，提高定位精度。

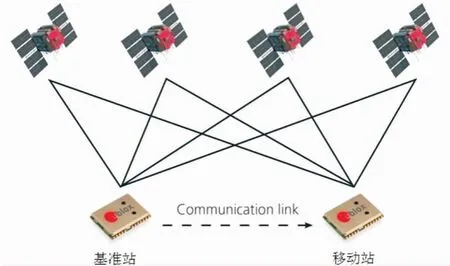
图1 PPK原理示意图

3 适用于单频GNSS接收机的差分算法

3.1 融合BDS/GPS的PPK解算方案

BDS和GPS采用几乎相同的观测方程，这就为BDS/GPS组合观测模型的建立提供了前提条件。假设在某一历元下，接收到M颗BDS卫星和N颗GPS卫星，那么组合观测模型如下：

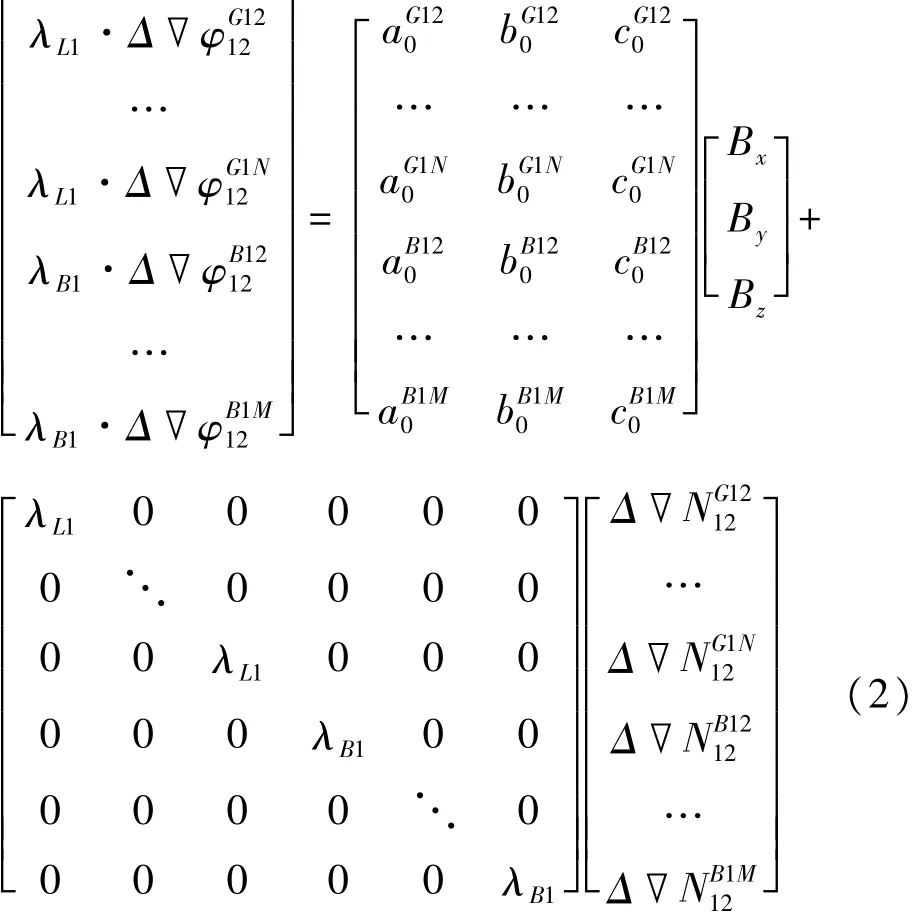
式中，λ代表载波波长;φ代表卫星载波相位观测量;N代表卫星载波整周模糊度;B代表基线向量。单频接收机相比于多频接收机对噪声更加敏感，采用BDS/GPS融合定位，同一时间内接收到的可用卫星数大大增加，尤其是在动态定位时，BDS/GPS双模定位比单GPS或单BDS定位更加稳定可靠、精度更高。

针对该低成本GNSS接收机自身的特点，本文解算方法采用单差代替双差载波相位模糊度以避免参考卫星的切换问题[6，7]，且该算法适用于移动站r和基准站b之间基线较短的情况，观测方程如下：

式中，Φ为载波相位;P为伪距;上标ij表示卫星间单差;下标rb表示接收机单差;ρ表示几何距离;λ表示波长;ε为噪声;表示单差分载波相位整周模糊度。RTK-GNSS差分定位中未知状态向量x定义如下：

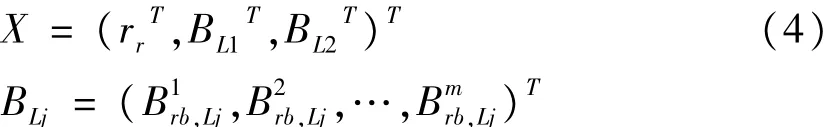
式中，rr是ECEF坐标系(地心地固坐标系)下移动站天线的位置。历元tk对应的观测矢量yk包含双差载波相位和伪距观测值[8]，表示如下：

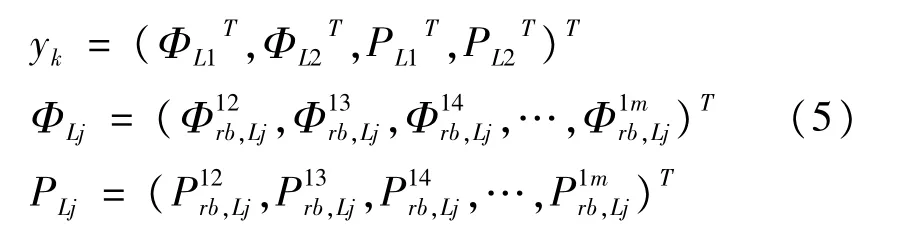
经过标准扩展卡尔曼滤波，估算状态矢量x和它的协方差矩阵P如下：

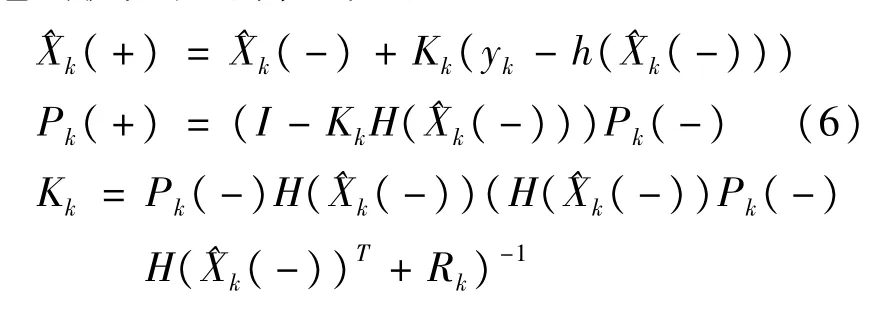
式中，h(x)、H(x)和Rk分别为观测误差的偏导数矩阵和协方差矩阵观测对应的模型矢量。因此，方程式(3)可以写成如下形式：

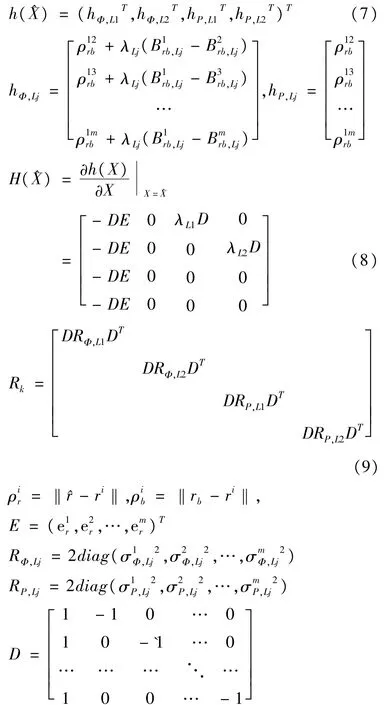
式中，ri是卫星i在ECEF(地心地固坐标系)下的位置;rb是基准站天线的位置;是移动站天线到卫星i的视线向量;D是单差矩阵。对于载波相位误差或伪距误差的标准差σ，本文算法是在用户自定义参数中采用高度角相关模型[9，10]。状态矢量的标准时间修正及其从历元tk到历元t(k+1)的协方差，通过扩展卡尔曼滤波表示如下：

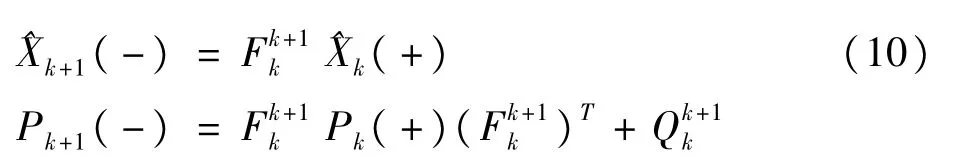
式中，F是状态传递矩阵;Q是系统噪声协方差矩阵。在动态定位模式中，白噪声模型通常假定，移动站天线位置如下：

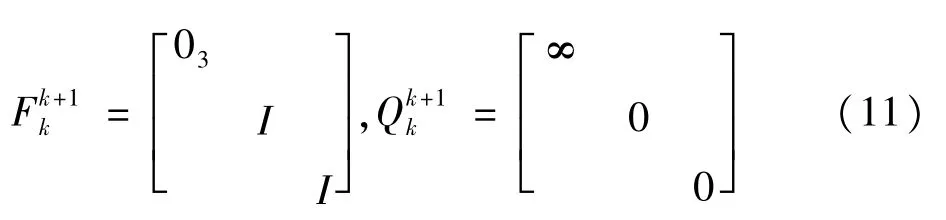
考虑到数值稳定性，本文算法将每个历元的移动站天线位置状态重置为单点解来代替纯动态模型。这种算法有效避免了非线性观测方程中的滤波器迭代计算，从而提高计算效率[11，12]。在静态定位模型中，本文使用单一转换模型，定义为F=I和Q=0。对于单差载波相位模糊度，初始状态定义为单差载波相位减去伪距观测值的估算值。如果探测到周跳，载波相位模糊度状态会以同样的方式重置为初始值[13]。本文采用无几何距离组合的周跳探测法。利用上述RTK-GNSS方程式解扩展卡尔曼滤波公式(6)，能得到估算的移动站位置和载波相位模糊度，估算的移动站位置常被用作无整周模糊度的浮点解。

3.2 基于LAMBDA算法的模糊度解算

获得估算状态后，需要将浮点型载波相位模糊度转化成整数，从而提高定位精度缩短收敛时间[14]。本文算法中，浮点解和协方差矩阵转换成单差形式如下：

式中，N是双差载波相位模糊度，需要通过消除接收机原始相位^关系进行整数化。在这种形式下，最佳整数矢量N需要满足整数最小二乘原理，表达如下：

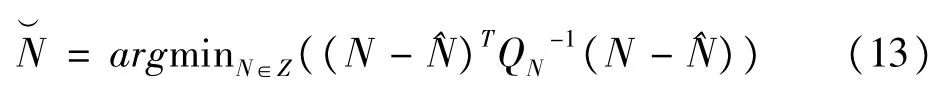
为了解决这个问题，引入广泛使用的LAMBDA算法及其扩展MLAMBDA算法[15]。通过简单的比值审检法校验，求解方程(14)便可获得移动站天线位置的固定解。

4 低成本定位系统

本次研究中使用的低成本GNSS接收机芯片为U-BLOX公司开发的NEO-M8T，该接收机芯片能够输出原始载波相位数据，而且价格低廉、性能稳定，是良好的试验选择[16]。低成本GNSS系统设计及组成如图2所示。

图2 低成本GNSS系统组成

①NEO-M8T为芯片的GNSS接收机：接收机的尺寸为4.6cm×3.9cm×0.5cm，重58g，具有差分GNSS功能，可以输出原始观测数据，其中包括L1频载波相位观测值。基准站通常以1Hz的更新频率记录观测数据，移动站最高可以设置10Hz采样频率。

②③数据记录与处理：GNSS接收机采集的数据可以通过串口连接到电脑上，并由特定软件进行数据解译和分析处理，直观地显示各种卫星信息。

④接收机天线：地面基准站一般使用测量型天线，机载移动站使用螺旋棒状轻型天线。

⑤电源：可USB供电或者锂电池供电。地面站多采用USB供电，机载移动端为减轻重量多采用小型锂电池供电，或者由无人机电源直接供电。

⑥数据传输端口：该接收机可以同时支持载波相位输出和NMEA0183格式数据。

⑦天线分离器及适配器：便于接收机连接不同的低成本天线和测量型天线进行试验。

为了进一步减轻重量并记录原始载波相位观测值进行PPK离线定位解算，机载端接收机(如图3所示)通过TF卡存储原始观测数据。

图3 具有TF卡存储功能的低成本GNSS接收机

5 定位精度验证

5.1 地面静态定位试验

为了测试该低成本高精度GNSS测量系统的定位精度和性能，试验以郑州市某高校为中心，展开三组基线长度分别为5km、10km、30km的静态测量。三组试验基准站天线和移动站天线均架设在坐标已知的控制点上，且四周开阔无遮挡，连续观测2小时并记录观测数据。对各组记录的原始观测数据进行解算，其结果见表1和图4。

结果表明：在基线长度5km条件下，定位精度优于1cm;在基线长度10km条件下，水平方向的定位精度在3cm以内，高程精度在5cm以内;当基线达到30km，平面定位精度在6cm以内，高程精度在10cm内。试验发现，虽然随着基线的增长定位精度有所下降，但是在30km范围内，该低成本定位系统定位性能稳定且精度达到测量型GNSS接收机的定位精度。通常情况下微小型无人机的航测作业范围在30km以内，因此，本文设计的低成本GNSS系统具有定位稳定、精度高的特点且满足无人机搭载的先决条件。

5.2 机载动态定位试验

低成本差分系统基准站架设情况如图5所示，用PC机存储原始数据，移动端搭载到双子星MTD无人机上，保证天线无遮挡。图6为试验用到的无人机平台以及移动站天线位置。试验过程中基准站先开机，然后接通移动站接收机电源，并静置10min。在地面站规划航线，此次动态试验共规划6条航线，飞行时间30min，设定相对航高500m。

图5 基准站

图6 固定翼无人机平台

对比传统无人机搭载的GNSS接收机单点定位精度(如图7所示)和本文差分定位算法的解算精度(如图8所示)可以发现，消除了单点定位10m的漂移误差，高程精度也提高了1个数量级，统计结果见表2。

表2 定位误差统计表(m)

表2统计了UTC时间08：00到09：00一小时内的定位误差，Sdx、Sdy、Sdz分别表示 x、y、z三个方向的标准差平均值。

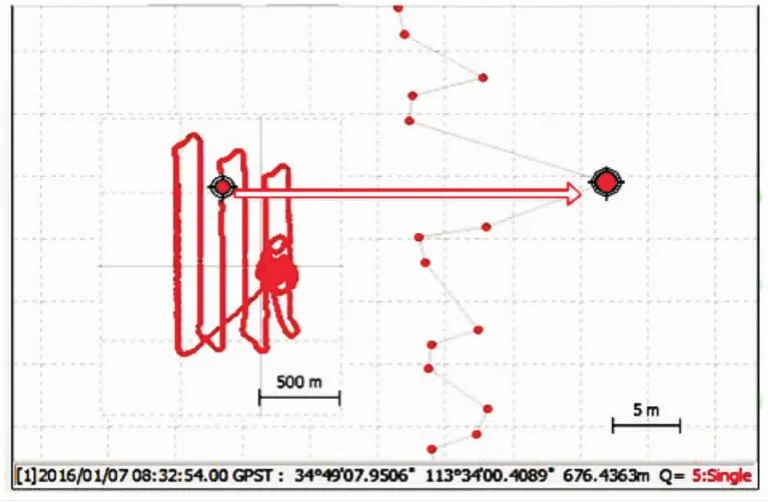
图7 单点定位解算精度

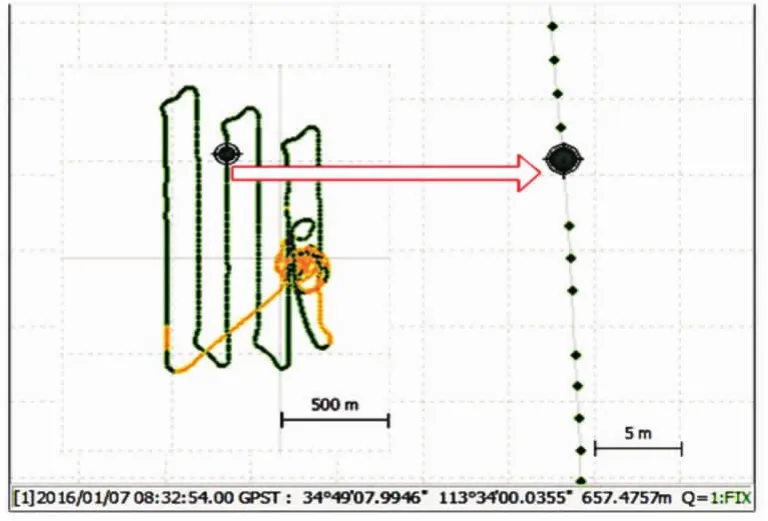
图8 本文差分算法解算精度

为了验证本文定位算法在动态定位中的优势，在新密市某测区飞行任务中规划航线10条，飞行时间50min。试验发现，传统的PPK算法对于单频接收机接收的数据存在大量的浮点解，影响定位精度。图9、10中绿色点代表固定解的点，黄色点代表浮点解的点，可以看出本文针对L1频数据改进的PPK算法将固定率从30.2%提高到93.9%。

图9 传统PPK模糊度解算

6 结束语

随着技术的发展和成熟，无人机平台小型化、轻型化的同时，成本也大大降低。针对目前传统POS系统体积大、质量大、价格昂贵，以及微小型无人机搭载的GNSS系统定位精度差等问题，本文利用U-BLOX的NEO-M8T芯片组成低成本GNSSPPK系统，该系统以成本低、精度高、体积小、质量轻等优势，为微小型无人机定位工作带来突破性进展。通过大量定位试验结合该单频接收机自身的特点，本文提出一种融合BDS/GPS的差分定位算法，极大地提高了定位精度：在30km基线范围内平面定位精度优于5cm，高程精度优于10cm。在模糊度解算过程中引入扩展MLAMBDA算法，提高动态定位中的固定解数量。试验表明该低成本GNSSPPK系统在无人机航测及精密农业等领域具有广阔的应用前景。但是由于该低成本GNSSPPK系统采样频率最高只有10Hz，考虑到无人机飞行速度快等问题，要想获得高精度摄影时刻的位置信息，必须采用拟合方法提高实际定位精度，并对天线相位中心位置和相机摄影中心位置进行严格的标定。这些实际问题的解决对无人机直接地理定位和大比例尺免像控低空摄影测量具有重大意义。

[1]徐绍铨，张华海，杨志强等.GPS测量原理及应用[M].武汉：武汉大学出版社，2008.

[2]Carcanague S.Low-cost GPS/GLONASSPrecise Positioning Algorithms in Constrained Environments[J].Toulouse Inpt，2013，12(23)：213-215.

[3]RehaMetinAlkan.Development of a Low-cost Positioning System Using OEM GPS Receivers and Usability in Surveying Applications[J].Building Challenges，2010，4(12)：204-206.

[4]周忠谟，易杰军，周琪.GPS卫星测量原理与应用[M].北京：测绘出版社，1997.

[5]Guo Hua Su.Research on Location Accuracy of UAV Based on DGPS/INSTechnique[J].Advanced Materials Research，2011，10(25)：204-210.

[6]刘琳.北斗/GPS双模差分定位技术的研究及实现[D].北京：北京交通大学，2013.

[7]Sun F P，Liu S，Zhu X U，et al.Research and Progress of BeiDou Satellite Navigation System[J].Science China Information Sciences，2012，55(12)：105-107.

[8]Jiang Z，Groves PD.NLOSGPSSignal Detection Using a Dual-polarisation Antenna[J].GPSSolutions，2012，12(1)：35-38.

[9]TomojiTakasu，Akio Yasuda.Evaluation of RTK-GPS Performance with Low-cost Single-frequency GPSReceivers[J].The Journal of the Japanese Forestry Society，2013，35(4)：338-340.

[10]Takasu，T.，and Yasuda.Evaluation of RTK-GPSPerformance with Low-cost Single-frequency GPSReceivers[J].International Symposium on GPS/GNSS，2008，11(14)：55-60.

[11]Tomoji Takasu，Akio Yasuda.Development of the Lowcost RTK-GPS Receiver with an Open Source Program Package RTKLIB[J].GPSSolutions，2012，16(3)：117-119.

[12]W.Stempfhuber and M.Buchholz.High-end and Lowcost RTK GNSSSystem for UAV Applications[J].Conference on Unmanned Aerial Vehicle in Geomatics，2011(4)：78-80.

[13]Will Hedgecock，MiklosMaroti，Janos Sallai，Peter Volgyesi，AkosLedeczi.High-accuracy Differential Tracking of Low-cost GPSReceivers[J].MobiSysJune，2013，6(13)：25-28.

[14]Teunissen，P.J.G.The Least-square Ambiguity Decorrelation Adjustment：A Method for Fast GPSAmbiguity Estimation[J].Journal of Geodesy，1995，9(70)：112-114.

[15]Chang X-W，Yang X.and Zhou T.A Modified LAMBDA Method for Integer Least-squares Estimation[J].Journal of Geodesy，2005，8(79)：379-381.

[16]Marek Dziewicki.Position Accuracy Evaluation of the Modernized Polish DGPS[J].Polish Maritime Research，2009，4(10)： 8-12.