星载激光测高系统误差分析
2017-05-02王昱,艾宇,吕源
王 昱,艾 宇,吕 源
1.西安测绘研究所,陕西 西安,710054;
2.地理信息工程国家重点实验室,陕西 西安,710054;
3.西安航天天绘数据技术有限公司,陕西 西安,710054
1 引 言
自从1974年“阿波罗”登月飞船上首次使用激光测高技术以来,包括美国、日本、中国等国家先后开展了星载激光测高技术的研究工作,国内外已经发射的典型激光测高卫星及其基本技术参数见表1[1-3]。

表1 国内外已经发射的典型激光测高卫星基本技术参数
美国于2003年发射的ICESAT卫星搭载了GLAS传感器,可测定沿轨道的陆地和水面的地形。由于GLAS获取的各级激光测高数据可以公开下载,已成为国内外学者从事星载激光测高技术研究的首选数据源。
ICESAT官方公布了其对GLAS传感器的高程确定精度分析结果,但没有给出完整的描述星载激光测高系统定位误差的数学模型。范春波[4]、朱剑锋[5]等提出了激光脚点定位模型,并给出了主要的误差源,但没有对脚点定位模型和误差源之间的关系进行理论分析。黄朝围[6]等利用简化模型分析了不同地形条件下星载激光测高精度的变化。马跃[7]利用简化模型分析了姿态对星载激光测高系统的影响,并利用南极地区的Li-DAR数据进行了高程精度检验试验。唐新明等[8]推导了激光测高卫星严密几何定位模型,并对光行差、硬件安装误差作了分析,但并未逐项分析激光测高的误差影响。文献[9-11]利用SRTM、机载LiDAR数据开展了针对GLAS数据的定位精度检验。
本文从星载激光雷达的精密几何定位模型出发,推导了各主要误差项对于激光雷达脚点几何定位的误差传播方程,利用仿真数据模拟了不同设计参数和误差条件下的定位误差。试验结果表明,姿态测量误差、指向角测量误差和距离测量误差对定位精度的影响较为剧烈。从获取满足无控定位精度要求的激光控制点的角度分析,在600km轨道高度,激光测高仪姿态测量和指向角测量精度应至少优于1.5″,测距精度应优于0.25m。
2 星载激光严密定位模型
本文涉及的主要坐标系定义如下:地心惯性坐标系OICRF-XICRFYICRFZICRF采用国际大地测量协会和天文学联合会于1984年启用的协议天球坐标系J2000;地固系OITRF-XITRFYITRFZITRF是以地球质心为原点,Z轴指向地球的北极,X轴指向格林尼治子午线与地球赤道交点,Y轴则按照右手法则确定;卫星本体坐标系OBody-XBodyYBodyZBody是以卫星的质心为原点,Y轴沿着卫星横轴,X轴沿着纵轴指向卫星飞行方向,Z轴按照右手法则确定;激光测高仪坐标系原点在测高仪质心,坐标轴与卫星本体坐标系平行。
星载激光测距的空间几何关系如图1所示。其中,图1(a)表示卫星本体坐标系 OBody-XBodyYBodyZBody、激光光线以及激光地面足印点在地心惯性系OICRF-XICRFYICRFZICRF中的位置关系;图1(b)则表示在激光测高仪坐标系中激光指向角θ、α的定义及其与激光脚点坐标的关系。在图1(a)中,Olaser为激光发射的参考点;PGNSS为GNSS天线相位中心;OBody为卫星质心;Pground为激光地面足印点。星载GNSS测定的是GNSS相位中心的位置;姿态敏感器测定的是星敏在J2000坐标系下的指向。为了得到激光脉冲发射时的位置和姿态,需要将GNSS和星敏测定的数据转化为激光测高仪的位置和指向,因此,需通过地面测定GNSS相位中心在卫星本体坐标系中3个偏移[Dx Dy Dz]T以及星敏感器本体系和卫星本体系之间的坐标旋转关系。同时,激光测高仪相对卫星本体之间也需测定位置偏移[dx dy dz]T及脉冲发射指向与卫星本体坐标轴的角度旋转之间的关系。
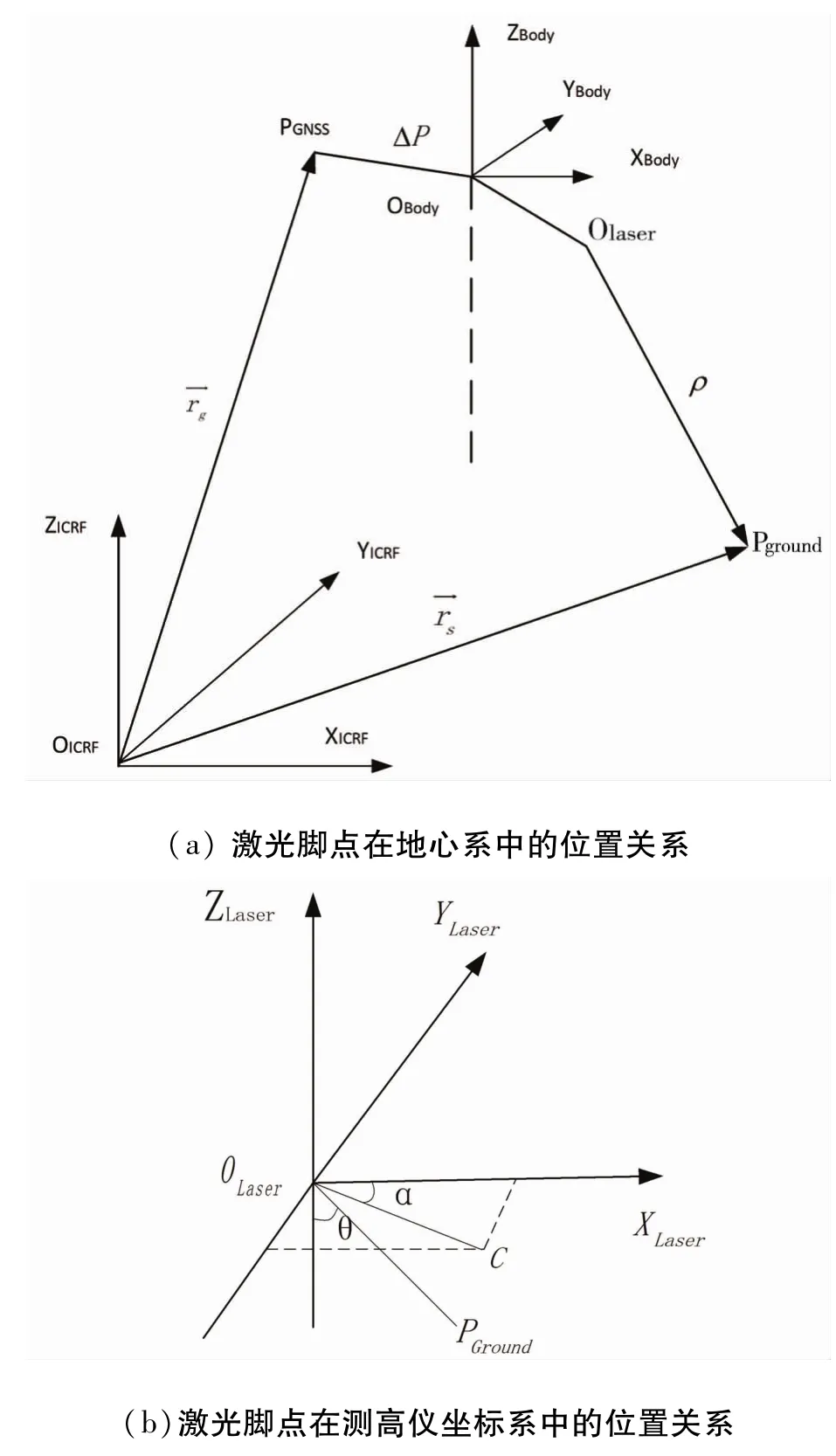
图1 星载激光测高原理
如图1(b)所示,假设激光指向与测高仪坐标系Z轴的夹角为θ,在XLaserOLaserYLaser平面上的投影OLaserC与 X轴正向夹角为α,ρ为激光的测距值,则激光脚点在卫星本体坐标系下的坐标为:
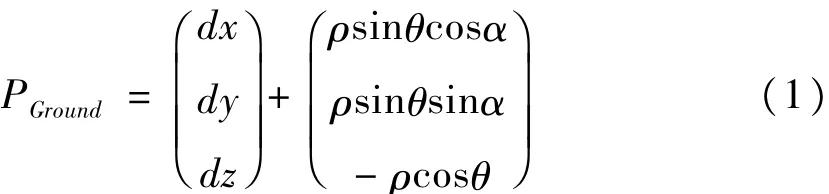
因此,在不考虑大气折射影响的条件下,在地固系中的星载激光测高严密几何定位模型为:
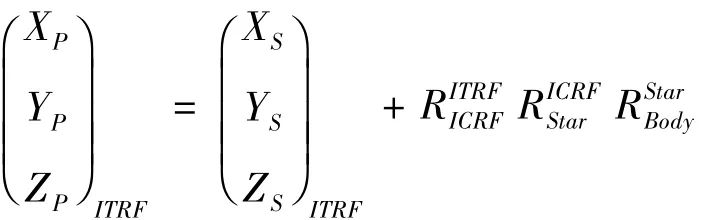
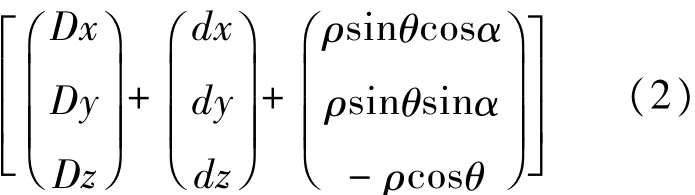
3 激光足印点定位误差源分析
对(2)式进行分析可以看出,激光足印点的定位精度主要受以下几项误差因素的影响:
一是卫星的质心定位误差,由星载GNSS接收机本身的定位误差以及内插计算引起。该项误差与其引起的定位精度变化是线性关系,影响有限。
三是激光测高仪的安置误差,包括GNSS偏心误差、激光参考点偏心误差、激光指向角误差三部分内容。其中两项偏心误差在实验室环境下的测定精度较高,尽管卫星在轨后会产生一定的变化,但其影响仍然相对较小。相比较而言,激光指向与卫星本体系的角度测量误差由于受测距值放大效应的影响会带来较大的误差,因此,是分析的重点。
四是激光测高仪的测距误差,主要为激光测高仪硬件测距误差和激光穿越大气层引起的传输误差,其中硬件测距误差可以通过标定和测量消除,传输误差可以通过后期处理修正。
因此,本文对于激光脚点误差的分析主要围绕位置定位误差 mXs、mYs、mZs,姿态测量误差 mφ、mω、mκ,指向角测量误差 mθ、mα和测距误差 mρ9个变量展开。假设上述9个变量取值相互独立,则对(2)式进行泰勒展开,取一次项得到(3)式。(3)式可以作为激光测距仪定位的误差传播方程,用于分析各误差项以及卫星设计值对于激光测高精度的影响。由于定位误差的影响有限,因此,下面重点分析姿态测量误差、指向角测量误差以及测距误差对激光脚点定位精度的影响。

3.1 姿态测量误差
姿态测量误差主要是卫星在轨运行时星敏、陀螺等仪器测量卫星姿态时产生的误差,可以分为俯仰φ、侧滚ω以及偏航κ三个正交方向的角误差分量。
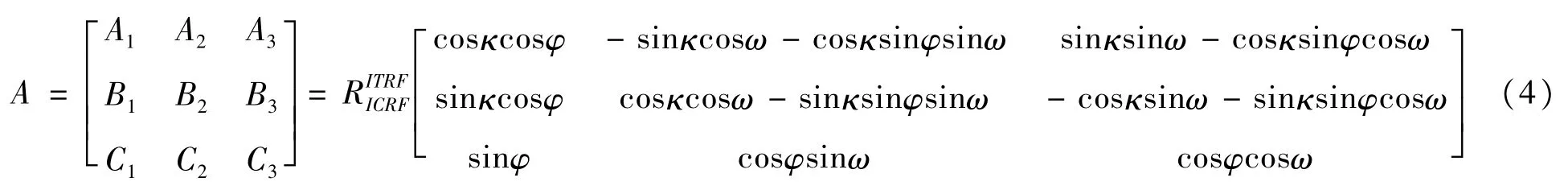
对(2)式求偏导,可得

3.2 指向角测量误差
正如前文所述,在安置误差中,由于GNSS和激光测高仪的偏心误差影响较小,而指向角误差受测距值影响对脚点定位精度产生的影响较大,因此,本节重点分析指向角误差。
分析(2)式可以看出,旋转矩阵A中的变量只和姿态角以及坐标系转换参数有关,和θ以及α角度即指向角无关。对(2)式求偏导可得,激光指向与激光测高仪本体坐标系Z轴夹角θ引起的误差可表示为:
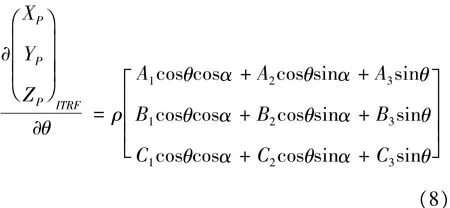
激光在XOY平面上的投影与X轴正向夹角α引起的误差可表示为:
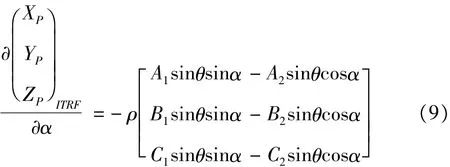
3.3 距离测量误差
星载激光测高仪的测距系统误差虽然在地面进行了严格的实验测定,但是入轨后其性能可能会受到影响。总的来讲,距离测量误差主要包括时间同步误差、地形起伏引起的定位误差及大气传输误差等,距离测量误差对激光脚点定位误差的影响可表示为:
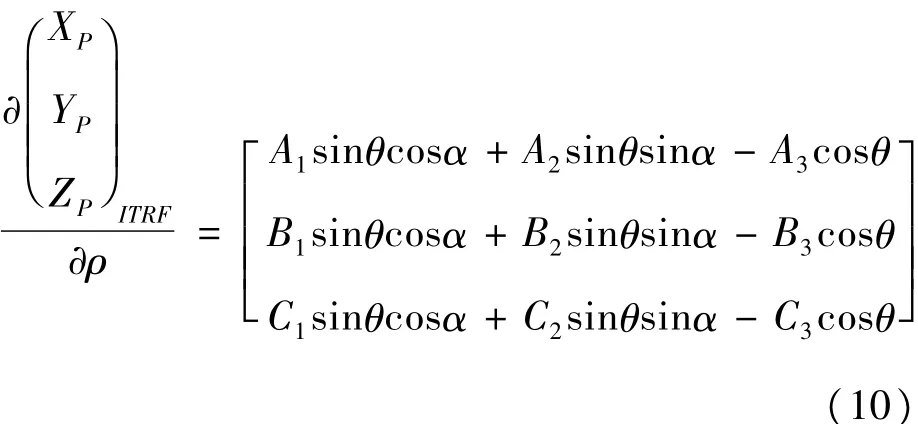
4 试验分析
为了系统分析卫星设计参数和定标误差对脚点定位精度的影响,参考ICESat及国内外同类卫星的设计使用情况,简化了公式(3)的分析条件,假设卫星质心及天线相位中心偏移量均为0,且在卫星飞行过程中,卫星姿态较为稳定,均为接近于0的微小角度,故将姿态角均设为0°。在同等测量误差情况下,飞行高度对定位精度的影响,近似认为,在此条件下,整理(3)~(10)式,得到三轴的误差传播方程如(11)式所示
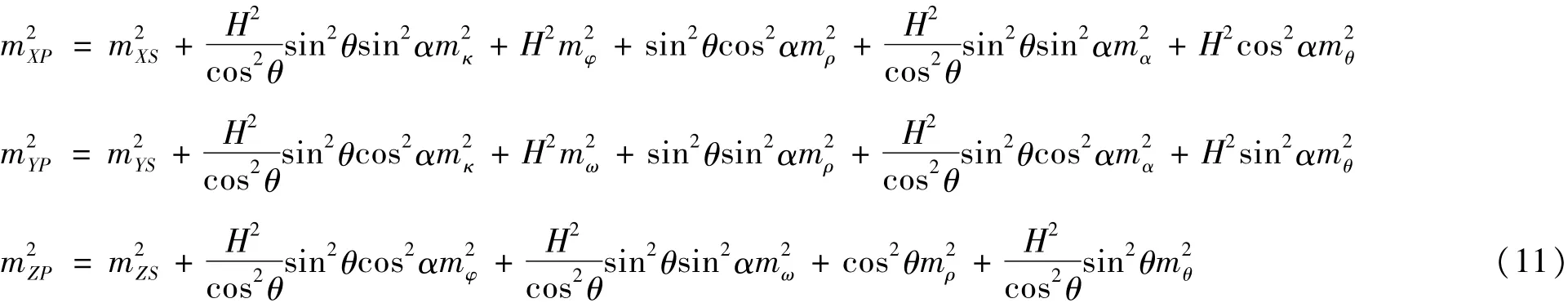
针对(11)式,重点分析卫星设计指标包括飞行高度H和指向角θ,以及测量误差包括平台定位误差、姿态测量误差、指向角测量误差以及测距误差对脚点定位精度的影响。
从卫星应用的角度分析,受星上能源条件限制,目前激光测高卫星获取的控制点密度还无法满足地形测量中DEM获取的密度要求,激光测高卫星获取的控制点或测距数据的用途主要是满足大比例尺测图中的精度提升需要,通过深入分析文献[12]提出的1:1万无控测图过程中的激光控制数据应用需求,在本文的仿真试验中,将激光控制点的精度要求设定为平面10m、高程1m。另外参考ICESat设计指标,除特别说明外,卫星飞行高度均为600km,指向角θ为0.3°,指向角α为90°,相关测量误差的取值考虑了国内外测距仪制造标定的平均水平,具体见表2。
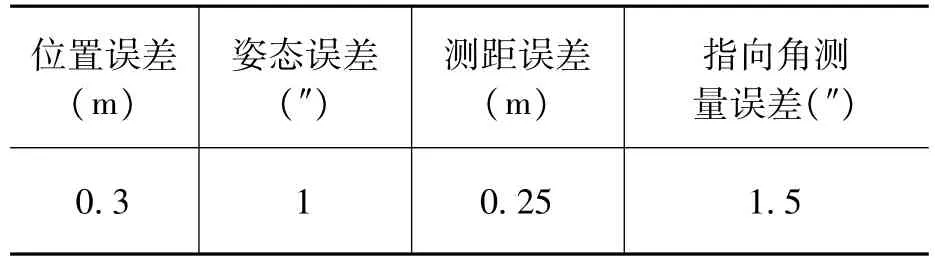
表2 测量误差的取值
4.1 卫星设计指标对脚点定位精度的影响
在各项测量误差不变的情况下,试验中分别改变轨道高度和指向角的设计参数,考察脚点定位误差变化对X、Y、Z三轴方向的误差 MX、MY、MZ以及总的定位误差MXYZ的影响情况。具体试验结果见表3和表4,其变化分析如图2和图3所示。

表3 飞行高度对定位精度的影响(m)

表4 指向角θ对定位精度的影响(m)

图2 飞行高度的影响
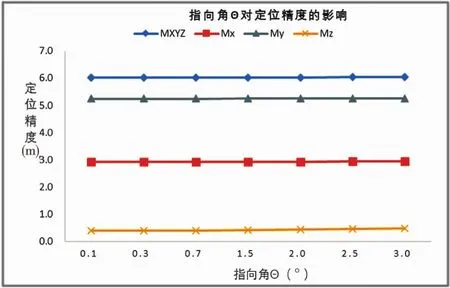
图3 指向角θ的影响
从表3和图2可以看出,在相同误差条件下,降低飞行高度,定位误差随之线性减小,这说明适当降低飞行高度有助于降低各项误差的影响。三轴方向的误差相互比较,平面X、Y方向变化较为剧烈,而Z方向则较为平缓,卫星高度从800km降至200km,Z方向误差仅减小了不到2cm。
分析表4和图3可以看出,相比飞行高度,指向角θ对定位误差的影响则相对较小,θ由0.1°提高到3°,总的定位误差值提高了约4cm。分析原因主要是指向角θ通过三角函数对定位误差产生影响,影响幅度有限。
指向角α对定位精度的影响见表5。仿真分析表明,该项设计值虽然对X、Y、Z方向的定位精度产生影响,但总的定位误差则没有发生明显变化。

表5 指向角α对定位精度的影响(m)
4.2 测量误差对于脚点定位精度的影响
各项测量误差中,平台位置测量误差的影响最简单,从(11)式可以看出,其对脚点定位精度的影响不仅是线性的,而且处在一个数量级上,图4的仿真结果也印证了上述结论。下面重点分析一下姿态测量误差、测距误差以及指向角测量误差的影响。
(1)姿态测量误差的影响
在其他条件不变的情况下,将姿态测量误差的取值由3″降到0.2″,脚点定位误差的变化情况见表6和图5。可以看出,随着姿态测量误差的减小,脚点定位精度迅速提升,特别是在X、Y方向变化非常显著,这种现象出现的原因主要是姿态测量精度影响了激光发射方向的确定精度,从而对脚点的平面定位精度产生了影响。从目前激光脚点10m的平面定位精度要求,并考虑一定富裕量,姿态测定精度应优于1.5″。

表6 姿态测量误差的影响(m)
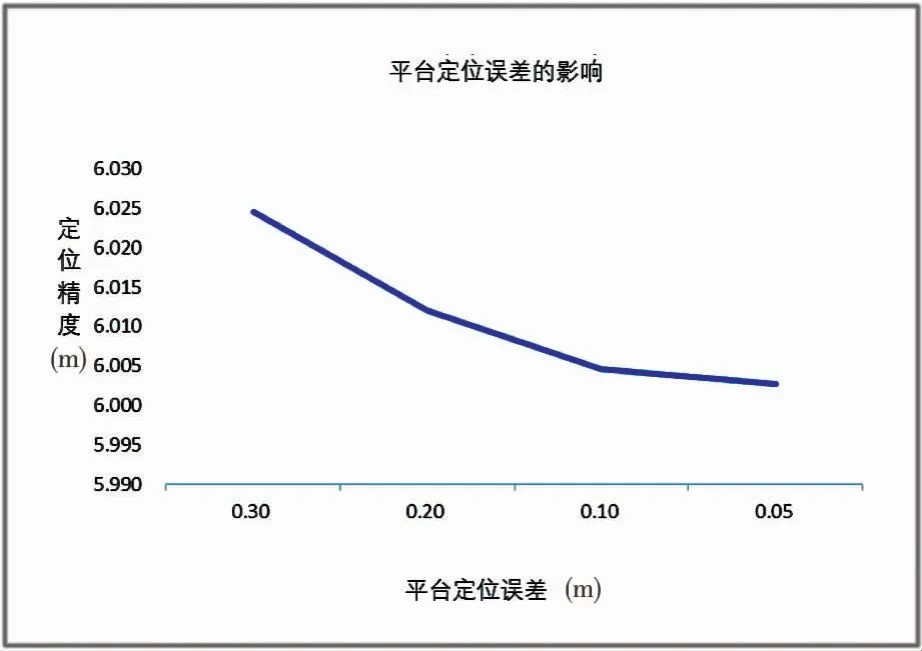
图4 平台定位误差的影响

图5 姿态测量误差的影响
(2)测距误差的影响
在其他条件不变的情况下,将测距误差由1m缩小到0.05m,定位误差的变化见表7和图6。可以看出,测距误差主要对Z方向的定位误差构成影响,且非常显著。应该指出在本次试验中,测距误差对于Y方向定位精度也有影响,因为发生在小数点6位以后,因此,在表6中没有显示出来,随着姿态确定误差的减小Y方向定位精度也不断提升。从目前对于激光控制点1m的高程定位精度要求并考虑激光测高仪的技术发展水平,测距误差应小于0.25m。
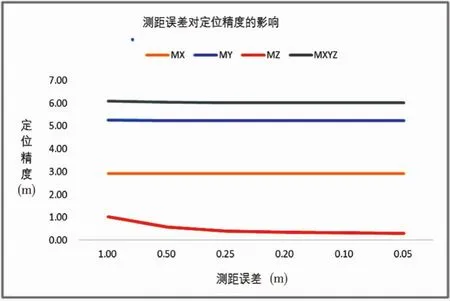
图6 测距误差的影响
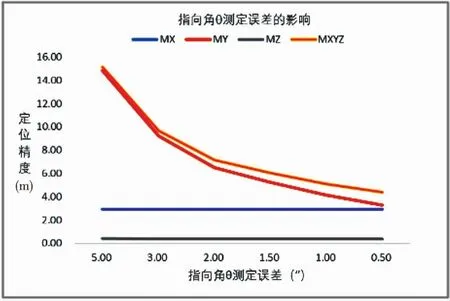
图7 指向角测量误差的影响
(3)指向角测量误差的影响
改变指向角θ的取值,由5″变化至0.5″,脚点误差的变化见表8和图7。可以看出,指向角对定位误差的影响类似于姿态测量误差的影响,主要影响平面定位精度,对Z方向的精度也有影响,但影响有限。至于影响X方向还是Y方向或者均影响,取决于α的取值。从满足目前激光控制点10m平面定位精度的要求并考虑指向角地面标定技术的发展,指向角测量精度应优于1.5″。
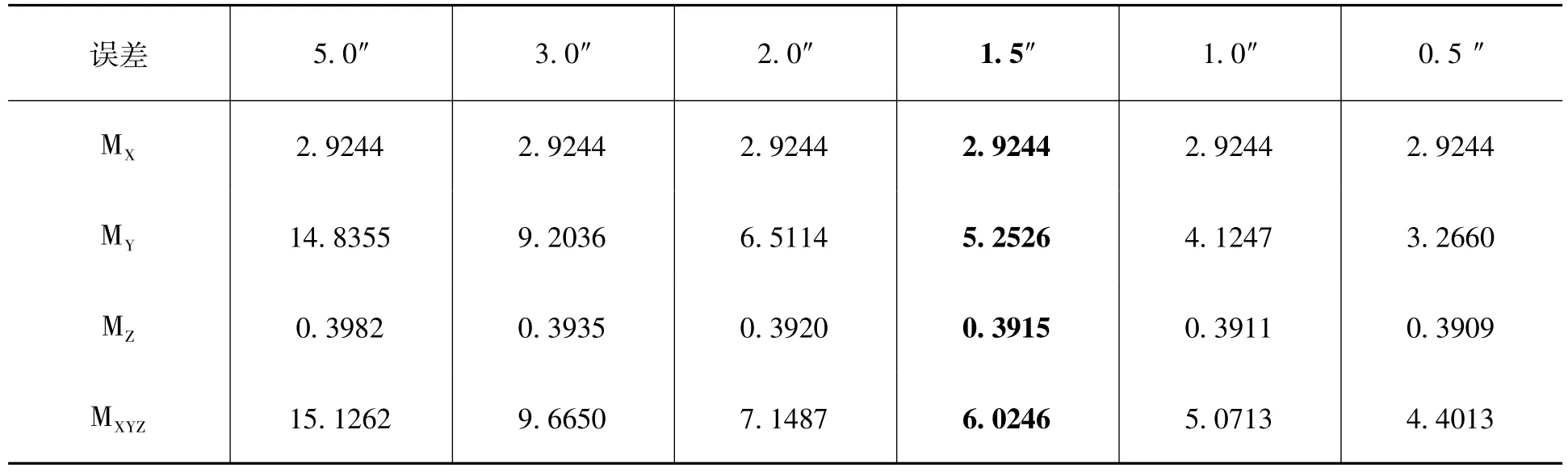
表8 指向角误差的影响(m)
应该指出姿态测量误差小于1.5″,测距误差小于0.25m,指向角测量误差小于1.5″的结论都不是单项误差独立影响的结果,而是在如表2所示的缺省误差条件(此时姿态测量精度1.0″)下得出的。事实上综合表6~8可以看出,当使用缺省误差条件时(字体加粗),三轴总的测量精度优于6.03m,平面定位精度优于6.02m,高程定位精度优于0.40m。在表6中还仿真了姿态测量精度1.5″,其他误差处于缺省条件的总的误差(表6中第四列字体加粗),其中三轴测量精度优于7.58m,平面定位精度优于7.57m,高程定位精度优于0.40m。
4.3 不同方向精度影响差异性的讨论
总结4.1、4.2节的试验不难看出,同样的误差,对于X、Y、Z三个方向精度影响有较大差异,除测距误差外,姿态测量误差、指向角测量误差对于X、Y方向定位精度影响较大,对于Z方向精度影响不大。为了分析造成这种影响的原因,选定一组典型参数 H=600km,θ =0.3°,α=90°,代入公式(11)得到:
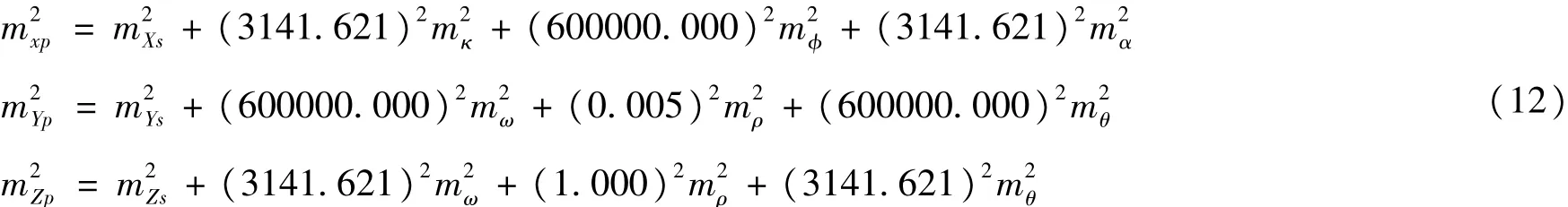
从(12)式可以看出飞行高度与测距值成正比,而飞行高度对于姿态和指向角测量误差的放大作用主要体现在X、Y方向(例如对于mω,影响因子是600000),对于 Z方向的影响相对较小(mω的影响因子3141.62),这就是Z方向精度变化小于X、Y方向的原因。同样测距误差的影响因子X、Y方向要远小于Z方向,这也解释了测距误差对于Z方向影响大于X、Y方向的原因。
同时仔细观察一下公式(11)会发现,除平台定位误差外,姿态误差、指向角误差以及测距误差在X和Y方向均关于角α成正余弦对称关系,如果在X方向误差因子中有sinα,则在Y方向误差因子中必然有cosα。其实回顾一下图1(b)中α的定义就会发现,这种规律的产生有其必然性,因为α本来就是用来定义激光光线在X、Y轴上的投影的。由于α取值一般是0°或90°,因此,各误差项对于X、Y的影响也成对称关系。例如当α=90°时,对X方向定位精度产生影响的误差项是mφ、mκ、mα,对 Y方向定位精度产生影响的误差项是 mω、mρ、mθ,这种对称现象在表5中得到了充分体现。随着α的变化X方向和Y方向的精度变化呈现此消彼长的特点,同时总的误差则几乎不变,这也解释了为什么在表7中指向角θ的误差只对Y方向精度产生影响。
5 结 论
本文从星载激光测高仪的严密定位模型出发,推导了各主要误差源的误差传播方程,利用仿真试验分析了各种误差源对于定位精度的影响。从试验结果看,姿态测量误差、指向角测量误差和测距误差对定位精度的影响较大。其中,姿态测量误差和指向角测量误差主要影响激光脚点的平面定位精度;测距误差则对高程定位精度的影响较为明显。
从满足卫星设计研制的角度分析,在激光测高仪技术状态确定的情况下,适当降低飞行高度有利于提高定位精度。在600km轨道高度激光测高仪如果需要满足平面10m、高程1m的定位精度,激光测高仪的姿态测量精度和指向角测量精度应至少优于1.5″,测距精度应优于0.25m。本次研究中,还未考虑地形坡度对于定位精度的影响,后续将开展深入研究。
[1]文汉江,程鹏飞.ICESAT/GLAS激光测高原理及其应用[J].测绘科学,2005,30(5):33-35.
[2]王建宇,舒嵘,陈卫标等.嫦娥一号卫星载激光高度计[J].中国科学,2010,40(8):1063-1070.
[3]韩玲,田世强,谢俊峰.星载激光测高仪检校技术发展现状浅析[J].航天返回与遥感,2016,37(6):11-19.
[4]范春波等.ICESAT/GLAS激光脚点定位及误差分析[J].大地测量与地球动力学,2007,27(1):104-106.
[5]朱剑锋,王昱,胡煜等.星载激光测高的系统误差分析与检校[J].测绘通报,2014(S1):137-140.
[6]黄朝围,李国元,李姗姗等.不同地形条件下的星载激光测高系统误差分析[J].测绘科学,2016,41(1):44-49.
[7]马跃,阳凡林,卢秀山等.对地观测星载激光测高系统高程误差分析[J].红外与激光工程,2015,44(3):1042-1047.
[8]唐新明,李国元,高小明等.卫星激光测高严密几何模型构建及精度初步验证[J].测绘学报,2016,45(10):1182-1191.
[9]艾建华.利用 ICESAT/GLAS激光测高数据评估SRTM数据精度[J].测绘技术装备,2015,17(2):63-66.
[10]Hieu Duong.Icesat Full-waveform Altimetry Compared to Airborne Laser Scanning Altimetry Over The Netherlands[J].IEEE Transactions on Geoscience and Remote Sensing,2009,47(10):3365-3378.
[11]Lori A,etc.ICESATAltimetry Data Product Verification atWhite Sands Space Harbor[J].IEEE Transactionson Geoscience and Remote Sensing,2007,45(1): 149-155.
[12]王任享.中国无地面控制点摄影测量卫星追述(二)1:1万传输型摄影测量卫星技术思考[J].航天返回与遥感,2014,35(2):1-5.
