Diagraph from power mapping on matrix rings over finite fields

Zhao Jinxing, Nan Jizhu

(1.School of Mathematical Sciences,Dalian University of Technology,Dalian 116024,China)

(2.School of Mathematical Sciences,Inner Mongolia University,Hohhot 010021,China)

Diagraph from power mapping on matrix rings over finite fields

Zhao Jinxing1,2, Nan Jizhu1

(1.School of Mathematical Sciences,Dalian University of Technology,Dalian 116024,China)

(2.School of Mathematical Sciences,Inner Mongolia University,Hohhot 010021,China)

For a finite ring or a finite group H written multiplicative,let G(H,k) be the digraph whose vertex set is H and there is directed edge from a∈H to b∈H if b=ak.In this paper,we study the k-th power mapping iteration graph from the matrix rings over finite fields.We obtain the distribution of indegrees and number of cycles of this digraph.

iteration digraph,finite field,tree,cycle length

1 Introduction

Let X be a non-empty set and f be a mapping from X into itself.Then we call G(X,f) the iteration digraph fromf of X,where the set of vertices of G(X,f)is X and there is a directed edge from a vertex a∈G(X,f)to a vertex b∈G(X,f)if f(a)=b.If R is a ring or a group written multiplicative and fmaps x to xk,then denote the digraph by G(R,k).

Many interesting examples of iteration graphs comes from the k-th power mapping of finite abelian groups or the ring of integers modulo n[1−5].The distribution of the indegrees and cycles of these digraphs are obtained.These results were soon generalized to the case for finite commutative rings[6−10].

This paper is motivated by[11],who investigate the structure of digraph form the generalized quaternion 2-group.This is the first paper concerned about the power digraph on a non-abelian group.In this paper,we study the k-th power mapping iteration digraphs of matrix rings over finite fields.Our main tool is linear algebra and group theory.

This paper is organized as follows.In Section 2,we present some basic properties of G(R,k)including indegees,cycles and structure of components.We point out that G(R,k) is a disjoint union of two induced sudigraph.In Section 3 and Section 4,we study the two induced subdigraphs independently.

2 Preliminaries and notations

Let Fqbe a finite field with q elements and R=M2(Fq)be the 2 by 2 matrix ring over Fqin the remaining part of this paper.Let U(R),Z(R),N(R)denote the set of units,zero-divisors and nilpotent matrices of R,respectively.We use fA(x)and mA(x)to denote the characteristic polynomial and minimal polynomial of A,respectively.The trace of A and determinant of A is tr(A)and detA.

A component of a digraph is a directed subgraph induced by a maximal connected subgraph of the associated undirected graph.A t-cycle of G(X,f)is a directed cycle of length t.A fixed point is a cycle of length 1.That is,f(x)=x.It is clear that if X is a finite set,then each component contains a unique cycle.The indegree of a vertex x∈X,denoted by(or indeg(x)),is the number of directed edges pointing to x.Thus,indeg(x)=|f−1(x)|.The height function on a vertex x is h(x)=mini≥0{fi(x)is a cycle vertex}.If C is a component of G(X,f),then we define h(C)=supx∈Ch(x).

There are two particular subdigraphs of G(R,k).Let G1(R,k)be the digraph induced subdigraph of G(R,k)on the set of units and G2(R,k)be the digraph induced subdigraph of G(R,k)on the set of zero-divisors.It is clear that G1(R,k)and G2(R,k)are disjoint and there are no edges between them.

Lemma 2.1[12]We have

(1)|U(R)|=(q2−q)(q2−1)=q4−q3−q2+q,

(2)|Z(R)|=q3+q2−q,

(3)|N(R)|=q2.

In the case that H is a finite abelian group,the structure of G(H,k)is highly symmetric. Let Cndenote the cyclic group of order n.Recall that if gcd(a,n)=1,the order of a modulo n is the minimal positive integer such that ak≡1(mod n).We need the following result.

Theorem 2.1Suppose that HCn1×Cn2×···×Cnr,where ni|ni+1for i= 1,2,...,r−1.Let k,k′be two positive integers and ni=uivi,where uiis the largest divisorof nirelatively prime to k.

(1)Any vertex of G(H,k)has indegree 0

(2)The number of cycle vertex of G(H,k)

(3)The set of cycle length appeared in G(H,k)is{orddk:d|ur}.

3 Structure of G2(R,k)

In this section we determine the structure of the induced subgraph of G(R,k)by the matrices of rank less than 2.

Lemma 3.1Let Zα={A∈Z(R):tr(A)=α}for α∈Fq.Then

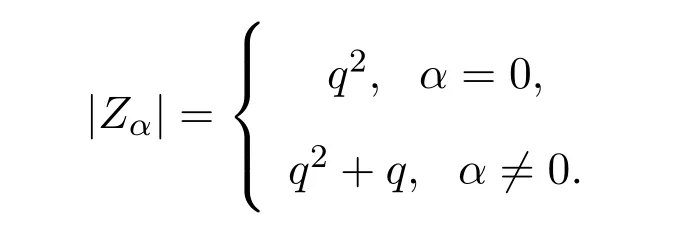
ProofClearly,Z0is the set of nilpotent matrices.By Lemma 2.1,we have

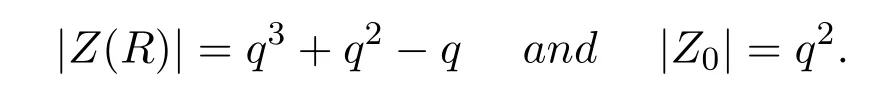
is bijective.It follows that|Zα|=|Zβ|for anyHence,

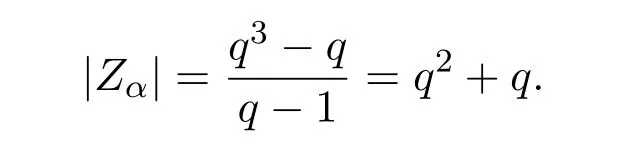
Lemma 3.2We define

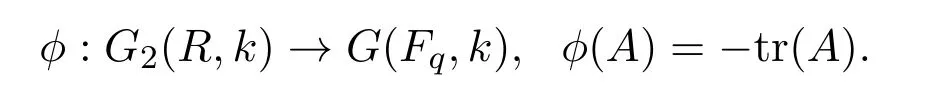
Then

(1)ϕ is a digraph homomorphism;

(2)ϕ|{cA:c∈Fq}is an isomorphism of digraph for any

ProofSince A2=tr(A)A for A∈Z(R),one has B=Ak=tr(A)k−1A.

Thus,B2=A2k=tr(A)2k−1A=tr(A)kAk=tr(A)kB and B∈Ztr(A)k.

So,ϕ|{cA:c∈Fq}is bijective and hence an isomorphism.

The proof is complete.

Theorem 3.1We have

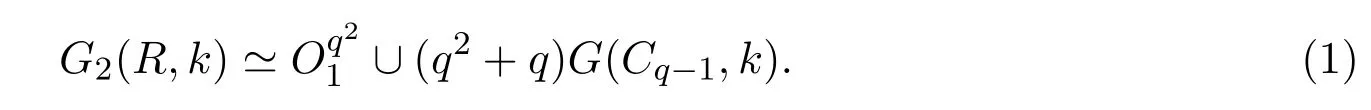
ProofLet YA=for any A∈Z(R).

Let Ai∈Zαisuch thatIf Ak=αkA=B for A∈Zα,then B∈YA.

It follows that there are no directed edge from the setto the set{cA2:c∈Thus,the digraph induced byis a union of components of G2(R,k).

The following is an immediate consequence of Theorem 3.1 and Theorem 2.1.

Corollary 3.1Let k1,k2be two positive integers and q−1=uv such that u is the largest divisor of q−1 relatively prime to k1.Then

if and only if gcd(q−1,k1)=gcd(q−1,k2)and orddk1=orddk2for any divisor d or u.

4 Structure of G1(R,k)

We recall some basic properties of polynomial over finite fields.

Lemma 4.1[13]Let g(x)∈Fq[x]and g(x)=be the irreducible factorization over Fqand degpi(x)=di.Then

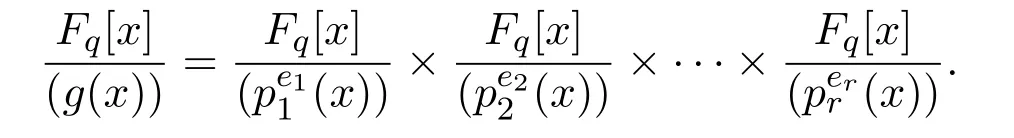
From now on,let V0denote the subspace of R consisting of scalar matrices.For any A∈U(R),let Fq[A]=

It is clear that dimFq[A]=2 if A is not a scalar matrix and dim(Fq[A]∩Fq[B])≥1.So Fq[A]=Fq[B]or Fq[A]∩Fq[B]=V0for any A and B.

The following lemma is simple but useful in our proof.

Lemma 4.2Suppose that Fq[A]Fq[B]for A,B∈R.If C∈Fq[A]V0and Ck∈Fq[B], then Ck∈V0.

ProofWe may assume that C=A since Fq[C]=Fq[A].Suppose to the contrary that AkV0.Then Ak=α1B+α2E=β1A+β2E for some α1β10.Hence B∈Fq[A],A∈Fq[B]and Fq[B]=Fq[A].It is a contradiction.

Lemma 4.3Let U be the unit group of Fq[A].Then

(2)If m(x)=(x−α)2,then

(3)If m(x)=(x−α1)(x−α2)and α1α2,then

(4)If m(x)is irreducible with degree 2 over Fq,then

ProofIf mA(x)is irreducible of degree d,thenThis proves statement(1)and(4).

If mA(x)=(x−α)2,then(x−α+1)q=(x−α)q+1,so x−α+1∈U with order q. Since gcd(q,q−1)=1,it follows thatThis proves(2).

If m(x)=(x−α1)(x−α2)and α1α2,then by Lemma 4.3 Fq[A]This proves(3).

Remark 4.1By Lemma 4.2 and 4.3,we have the following union

where dimFq[Ai]=2 and Fq[Ai]∩Fq[Aj]=V0for distinct i,j.Let Uibe the unit group of Fq[Ai].After ordering we may assume that

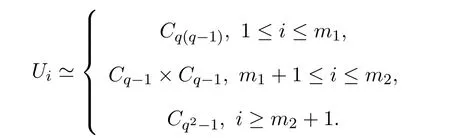
Now we count the number in the decomposition(2).

Lemma 4.4Let Uibe the unit group of Aiin equation(2),m1=and m3=Then m1=q+1,m2=and

ProofLet Zibe the set of zero-divisor of Fq[Ai].Then Ziis nilpotent if and only if

By Lemma 2.1 the number of nilpotent elements in R is m1(q−1)+1=q2.So m1=q+1.

By Lemma 2.1 again,the number of zero-divisor of R is q2+m2(2q−2)=q3+q2−q.So

Finally,|R|=(m1+m2+m3)(q2−q)+q=q4.So m3=

Now we can determine the distribution of indegrees and length of cycles in G1(R,k).

Theorem 4.1Suppose that A∈U(R)and

(4)If A∈V0,then

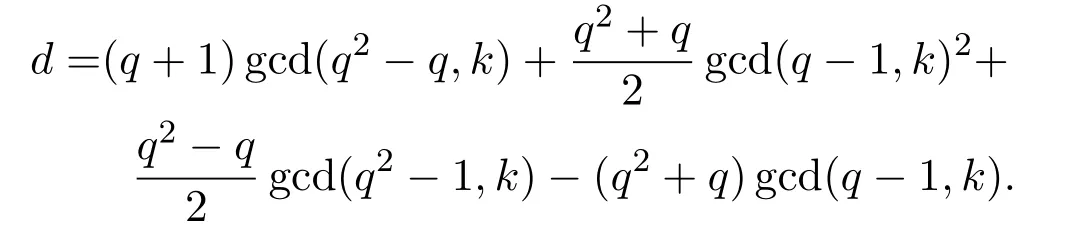
ProofIf AV0and Bk=A,then B∈Fq[A]by Lemma 4.2.Since both B and A are invertible,one has d=gcd(q(q−1),k),by Lemma 2.1.

This proves statement(1)and the proof of(2)and(3)are similar.

Now suppose that A∈V0and R=be the union in(2)and Uibe the unit group of Fq[Ai].By Lemma 4.1,we have the following disjoint union

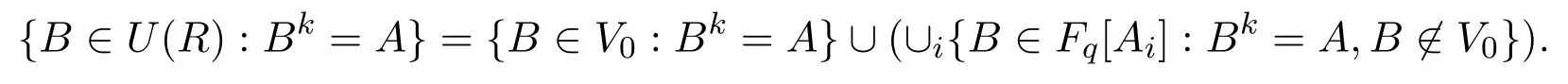
By Theorem 2.1,

Combining with m1=q+1,,we obtain(4).

A digraph G is called semiregular if there exists a positive integer d such that the indegree of any vertex of G is d or 0.

Corollary 4.1G1(R,k)is semiregular if and only if gcd(q3−q,k)=1.

ProofIf gcd(q3−q,k)=1,then by Theorem 4.1 and a simple computation we see that any vertex in G1(R,k)has indegree 0 or 1.

Conversely,suppose that G1(R,k)is semiregular.By(1)and(2)of Theorem 4.1,we have

Since gcd(q−1,q)=1,one has

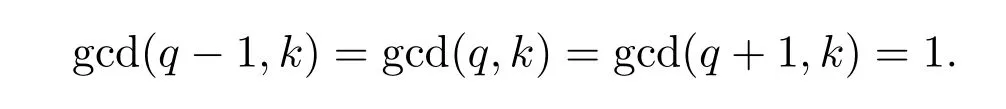
Thus,gcd(q3−q,k)=1.

Theorem 4.2Let q2−1=u1v1,q=u2v2where uiis the largest divisor of q2−1,q (resp,)relative prime to k.Then the set of cycle length appeared in G1(R,k)is

and the number of fixed point in G1(R,k)is

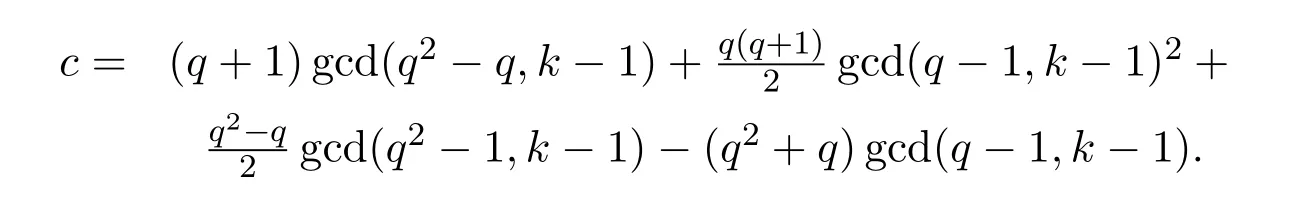
ProofLet A1,A2,...,Atbe a t-cycle contained in G1(R,k).Clearly,all Aiare scalar matrices if and only if one Aiis a scalar matrix.

Let cibe the number of fixed points in UiV0.So ciis equal to the number of fixed points of G(U,k)minus the number of fixed points in G(Cq−1,k).By Theorem 2.1,we have

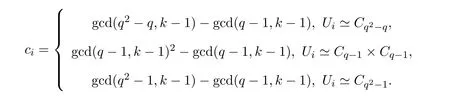
Thus,the number of fixed points in G1(R,k)is equal to c.

Corollary 4.2Let

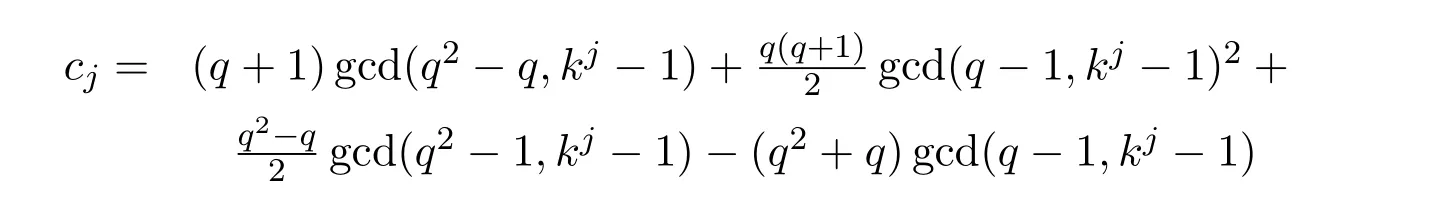
be the number of fixed points in G1(R,kj).

Then the number of t-cycle in G1(R,k)is ct−

ProofIt follows immediately from that x is contained in a t-cycle of G1(R,k)if and only if x is a fixed point in G1(R,kt).

Reference

[1]Deng G X,Yuan P Z.Isomorphic digraphs from powers modulo p[J].Czechoslovak Math.J.,2011,61:771-779.

[2]Lucheta C,Miller E,Reiter C.Digraphs from powers modulo p[J].Fibonacci Quart.,1996,34:226-239.

[3]Rogers T D.The graph of the square mapping on the prime field[J].Discrete Math.,1996,148:317-324.

[6]Deng G X.On the structure of G(H,k)[J].Algebra Colloq.,2014,21(2):317-330.

[7]Meemark Y,Wiroonsri N.The quadratic digraph on polynomial rings over finite fields[J].Finite Fields Appl.,2010,16:334-346.

[8]Meemark Y,Wiroonsri N.The digraph of the kth power mapping of the quotient ring of polynomials over finite fields[J].Finite Fields Appl.,2012,18:179-191.

[9]Wei Y J,Nan J Z,Tang G H.Structure of cubic mapping graph for the ring of Gaussian integers modulo n[J].Czechoslovak Math.J.,2012,62:527-539.

[10]Wei Y J,Nan J Z,Tang G H.The square mapping graphs of finite commutative rings[J].Algebra Colloq., 2012,19:569-580.

[11]Ahmad U.The classification of finite groups by using iteration digraphs[J].Czechoslovak Math J., 2016,66(4):1103-1117.

[12]Morrison K E.Integer sequences and matrices over finite fields[J].J.Integer Seq.,2006,9:06.2.1.

[13]Lidl R,Niederreiter H.Introduction to finite Fields and Their Applications[M].England:Cambridge University Press.1994.

有限域上矩阵环的幂映射图

赵金星1,2,南基洙1

(1.大连理工大学数学科学学院,辽宁,大连 116024)

(2.内蒙古大学数学科学学院,内蒙古,呼和浩特 010021)

对于一个环或者是乘法群H和一个正整数k,我们可以定义一个有向图G(H,k),称为H上的k次幂映射图.它的顶点集合就是H,并且从a到b有一条有向边当且仅当b=ak.交换环或者交换群上的k次幂映射图一般具有较好的对称性,这方面已经有相当多的结果.本文研究有限域上二阶矩阵环的k次幂映射图,利用线性代数和群论的方法,克服了非交换性带来的困难,得到了这类图的顶点入度的分布和圈长的分布.

迭代图;有限域;树;圈的长度

O157.5

2016-12-29.

国家自然科学基金(11371343).

赵金星(1979-),硕士生,讲师,研究方向：代数学及其应用.

A

1008-5513(2017)02-0152-08

10.3969/j.issn.1008-5513.2017.02.006

2010 MSC:05C05,05C20,05C25,05C38