平衡对和完备余挠对

孙丹,杨晓燕

(西北师范大学数学与统计学院,甘肃 兰州 730070)

平衡对和完备余挠对

孙丹,杨晓燕

(西北师范大学数学与统计学院,甘肃 兰州 730070)

通过讨论平衡对、相对于平衡对的特殊逼近和相对于平衡对的余挠对之间的关系,给出了它们的一些性质,并得到了相对完备余挠对的等价刻画.

平衡对;相对特殊逼近;相对余挠对

1 引言

在经典同调代数中,平衡对占据很重要的位置.比如,文献[1]中介绍了左(或右)平衡函子的概念.文献[2]中将左(或右)平衡函子应用到了相对同调代数中.近年来,文献[3]中介绍了阿贝尔范畴中加法子范畴平衡对的概念,并证明了阿贝尔范畴中的平衡对,遗传了经典平衡对中一些很好的性质.余挠对的概念最早是由文献[4]中提出的.因为余挠对的定义是以函子Ext(−,−)为基础的,所以余挠对的本质是以平衡对为基础的.因此,通过平衡对来研究相对于平衡对的余挠对的性质是很有意义的.2016年,文献[5]中在阿贝尔范畴中,定义了相对于平衡对的余挠对的概念,给出了相对完备余挠对的一些等价刻画.受到这些工作的启发,本文继续研究了相对完备余挠对的等价刻画.

2 准备知识

在本文中,A是阿贝尔范畴,A的子范畴是在同构和直和项下封闭的加法满子范畴, P(A)是A中的投射对象构成的子范畴,I(A)是A中的内射对象构成的子范畴,C(A)是A中对象的复形构成的范畴.

定义 2.1[3,5]设X是A的一个子范畴,

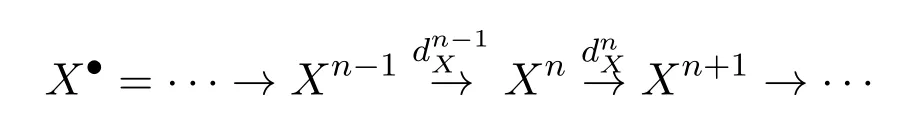
(1)称复形X•是零调的(或正合的),如果对任意的i∈Z,有Hi(X•)=0.

(2)称复形X•是右X-零调的,如果对任意的X∈X,复形HomA(X,X•)是零调的.

定义 2.2[6]设 X,Y是 A的子范畴且 X ⊆Y,f:X→Y是 A中的态射,其中X∈X,Y∈Y.

(1)称f是Y的右X-逼近,如果对任意的X′∈X和A中任意的态射g:X′→Y,都存在态射h:X′→X,使得下图交换

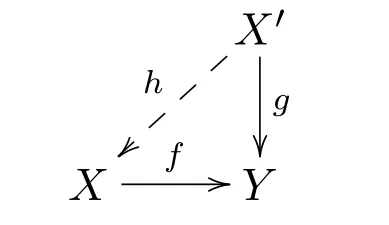
(2)称X是Y的反变有限子范畴,如果Y中的每一个对象都有右X-逼近.类似地,可以定义左X-逼近和共变有限子范畴的概念.

定义 2.3[5]称A的反变有限子范畴X是容许的,如果每一个右X-逼近是满的.类似地,可以定义余容许子范畴的概念.

定义 2.4[3,7]设X是A的反变有限子范畴,M∈A.称复形X是M的X-分解,如果A中的复形

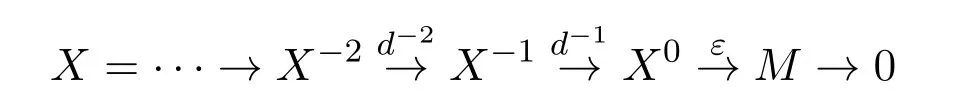
是右X-零调的,其中Xi∈X.通常将该分解记为其中

是M的删项X-分解.类似地,可以定义Y-余分解的概念.

3 平衡对和完备的余挠对

定义 3.1[3,7]设X,Y是A的子范畴.称(X,Y)是平衡对,如果满足以下条件:

(1)X在A中是反变有限的,Y在A中是共变有限的;

(2)对任意的M∈A,都存在M的左Y-零调的X-分解X•→M;

(3)对任意的N∈A,都存在N的右X-零调的Y-余分解N→Y•.

因此,(X,Y)是平衡对当且仅当右X-零调复形的类与左Y-零调复形的类是一致的.

例 3.1[7]设R是n-Gorenstein环,Mod R是左R-模范畴.GP(R)是由Gorenstein-投射模构成的Mod R的子范畴,GI(R)是由Gorenstein-内射模构成的Mod R的子范畴.则(GP(R),GI(R))是Mod R的平衡对.

定义 3.2[5,7](1)称复形X是∗-零调的,如果X既是右X-零调的又是左Y-零调的.

(2)设(X,Y)是平衡对,M,N∈A,X•→M是M的X-分解,N→Y•是N的Y-余分解.对任意的i∈Z,定义上同调群

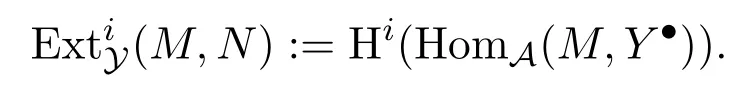
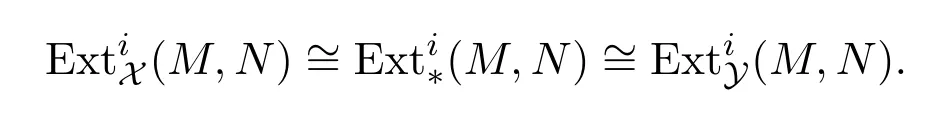
(3)设E是A的子范畴,f:E→M是M的右E-逼近,其中M∈A,E∈E.称f相对于平衡对(X,Y)是特殊的,如果f是满的且Ker f∈E⊥∗,其中

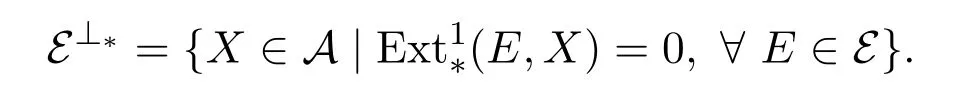
类似地,我们可以定义相对于平衡对(X,Y)的特殊左E-逼近.

(4)设(X,Y)是平衡对,C,D是A的子范畴.称(C,D)是相对于(X,Y)的余挠对,如果C=⊥∗D,D=C⊥∗,其中⊥∗D=

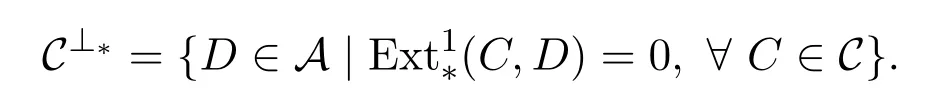
在本节的其余部分,(X,Y)指的是A中的平衡对,(C,D)指的是相对于(X,Y)的余挠对.

命题 3.1[5]X是容许的当且仅当Y是余容许的.此时,称(X,Y)是容许的.

定理 3.1设E是A的子范畴.

证明(1)因为φ:E→M是相对于(X,Y)的特殊右E-逼近,所以φ是满的且

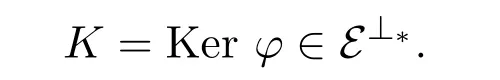
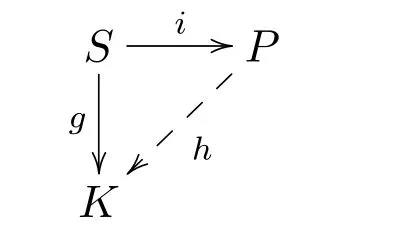
即g=hi.设ε:K→M是包含映射.令f=εg,则f=εhi,即f可通过i分解.同理可证 (2).

命题 3.2设(C,D)和(D,F)是相对于(X,Y)的遗传余挠对.若(X,Y)关于直和项封闭,则C∩D=X,D∩F=Y.

证明因为(C,D)和(D,F)是相对于(X,Y)的遗传余挠对,所以由文献[5]和命题3.7知,

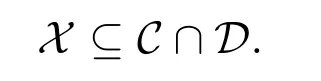
故对1M∈HomA(M,M),存在γ∈HomA(M,X),使得β∗(γ)=1M,即βγ=1M.

因为 X关于直和项封闭,所以 M∈X.故 C∩D⊆X.因此 C∩D=X.同理可证D∩F=Y.

定义 3.3[7](1)称(C,D)有足够投射对象,如果对任意的M∈A,都存在A中的一个∗-零调的复形0→D→C→M→0,其中C∈C,D∈D.

(2)称(C,D)有足够内射对象,如果对任意的M∈A,都存在A中的一个∗-零调的复形0→M→D→C→0,其中C∈C,D∈D.

(3)称(C,D)是完备的,如果(C,D)有足够投射对象和足够内射对象.

由前面可知,由平衡对可以得到与之相关的余挠对.下面我们说明,由(X,Y)上的余挠对可以构造出新的平衡对.

命题 3.3设 (C,D)和 (D,F)是相对于 (X,Y)的完备遗传余挠对,(X,Y)是容许的.则(C,F)是一个平衡对.

证明任取N∈A.因为(D,F)是完备的,所以(D,F)有足够内射对象,即存在A中的一个 ∗-零调的复形其中 F∈F,D∈D.下证:若 C∈C,则HomA(C,F)→HomA(C,D)→0是零调的.取A中∗-零调的复形

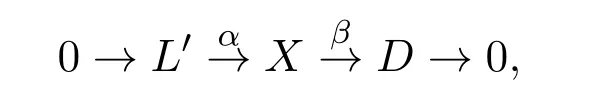
其中X∈X.由[5,命题3.7]知,X∈X⊆D,D∈D,(D,F)是遗传的,所以L′∈D.因为=0,所以用函子HomA(C,−)作用得零调的复形

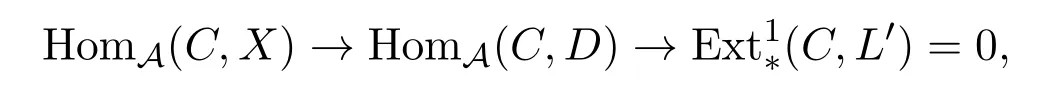
即HomA(C,X)→HomA(C,D)→0是零调的.

故对任意的a∈HomA(C,D),存在b∈HomA(C,X),使得a=βb.又因为

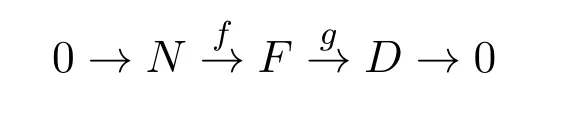
是右X-零调的,所以

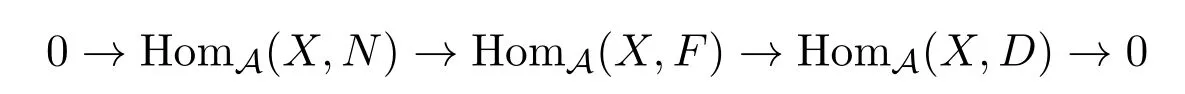
是零调的.故对β∈HomA(X,D),存在c∈HomA(X,F),使得β=gc.因此,a=βb=gcb,即对任意的a∈HomA(C,D),存在bc∈HomA(C,F),使得a=HomA(C,g)b=gcb.从而

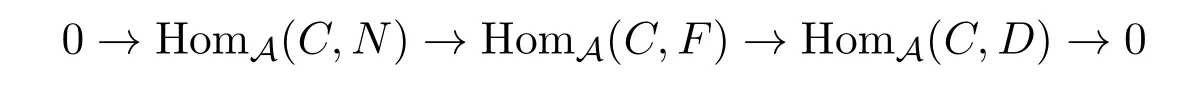
是零调的.因为(X,Y)是容许的,所以每一个∗-零调的复形是零调的,继续这个过程

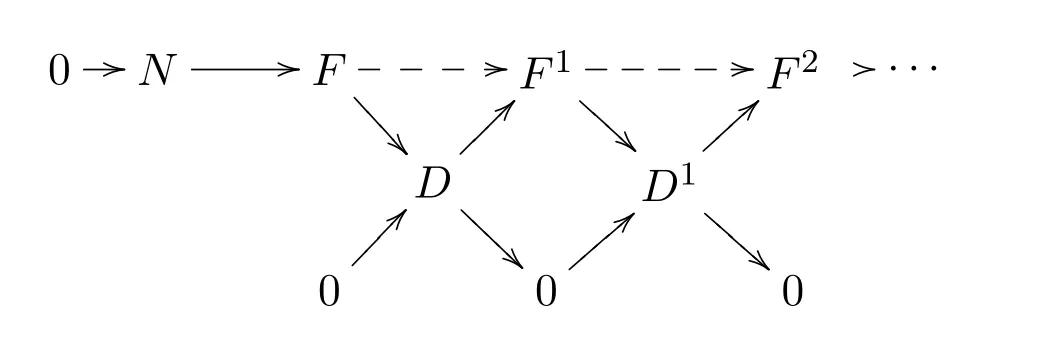
对任意的N∈A,可以得到右C-零调的F-余分解N−→F•.对偶地,对任意的M∈A,可以得到左F-零调的C-分解C•−→M.因此,(C,F)是一个平衡对.

由余挠对完备的定义,我们有以下完备的等价刻画:

定理 3.2设(X,Y)是容许的,(C,D)是遗传的余挠对.则以下等价:

(1)(C,D)是完备的;

(2)A的每一个对象有相对于(X,Y)的特殊右C-逼近且C的每一个对象有相对于(X,Y)的特殊左D-逼近;

(3)A的每一个对象有相对于 (X,Y)的特殊左 D-逼近且 D的每一个对象有相对于(X,Y)的特殊右C-逼近.

证明(1)⇔(2)与(1)⇔(3)类似.只证(1)⇔(2).

(1)⇒(2)因为(C,D)是完备的,所以(C,D)有足够投射对象,即对任意的M∈A,都存在A中的一个∗-零调的复形其中C∈C,D∈D.故

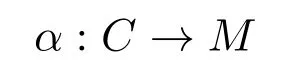
是A中对象M的相对于(X,Y)的特殊右C-逼近.因为(C,D)是完备的,所以(C,D)有足够内射对象,即对任意的M∈A,都存在A中的一个∗-零调的复形其中C′∈C,D′∈D.特别地,取N∈C⊆A,存在A中的一个∗-零调的复形其中C′∈C,D′∈D.故α′:N→D′是C中对象N的左D-逼近且Coker又因为α′是单的,所以α′:N→D′是C中对象N的相对于(X,Y)的特殊左D-逼近.

(2)⇒ (1)设 φ:C→M是A中对象 M的相对于 (X,Y)的特殊右 C-逼近.因为 (X,Y)是容许的,所以存在 A中的一个 ∗-零调的复形0,其中K==D.设ψ:C→D′是C中对象C的相对于(X,Y)的特殊左D-逼近.则存在A中的一个∗-零调的复形其中=C.因为C,C′∈C,(C,D)是遗传的,所以D′∈C,即D′∈C∩D.考虑下面的推出图

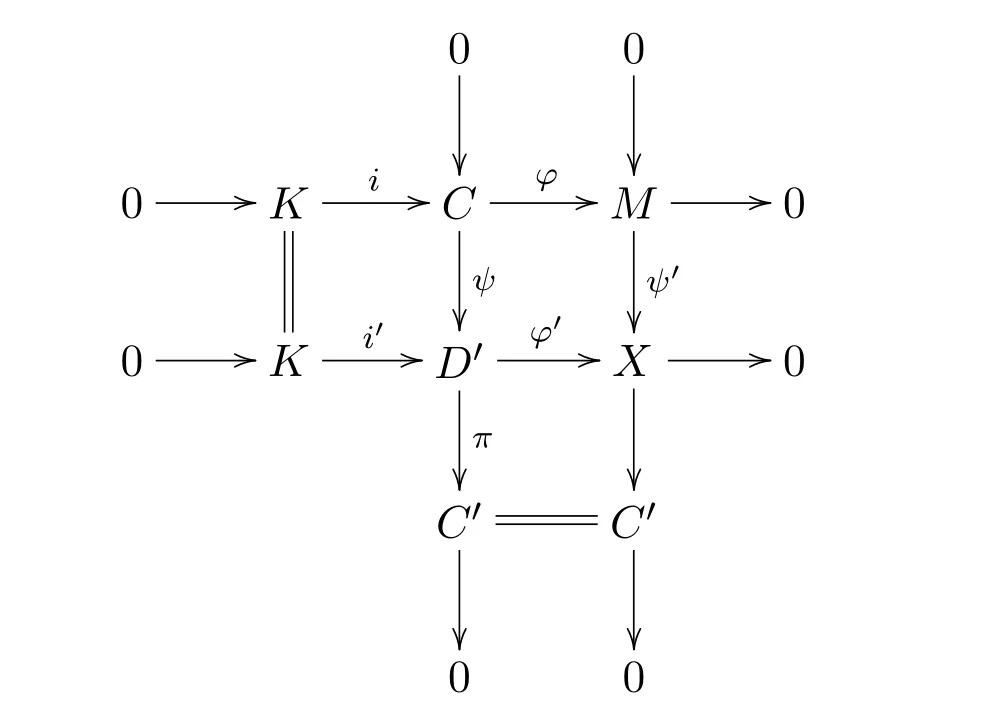
并且存在一个态射j:D′→Y,使得g=jψ.

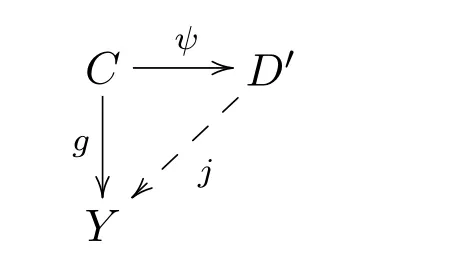
因此,f=gi=jψi=ji′且0→0是∗-零调的.因为(C,D)是遗传的,所以

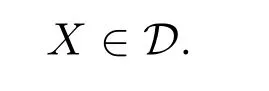
下证:ψ′:M→X是 A中对象 M的相对于 (X,Y)的特殊左 D-逼近.即证:ψ′是单的且 Coker因为0是 ∗-零调的,所以 ψ′是单的且又因为C′∈C,C关于同构封闭,所以

因此,ψ′:M→X是A中对象M的相对于(X,Y)的特殊左D-逼近.故对任意的M∈A,有A中的∗-零调的复形其中C∈C,Ker φ∈D和A中的∗-零调的复形

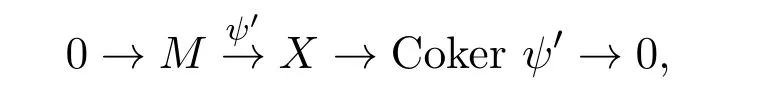
其中Coker ψ′∈C,X∈D.因此,(C,D)有足够投射对象和足够内射对象,即(C,D)是完备的.

[1]Cartan H,Eilenbery S.Homological Algebra[M].Princeton:Princeton University Press,1956.

[2]Enochs E E,Jenda O M G.Balanced functors applied to modules[J].J.Algebra,1985,92:303-310.

[3]Chen X W.Relative singularity categories and Gorenstein-projrctive modules[J].Math.Nachr.,2011,284:199-212.

[4]Salce L.Cotorsion Theories for Abelian Categories[M].Cambridge:Cambridge University Press,1979.

[5]Li H H,Wang J F,Huang Z Y.Applications of Balanced Pairs[J].Sci.China Math.,2016,59:861-874.

[6]Auslander M,Reiten I.Applications of contravariantly finite subcategories[J].Adv.Math.,1991,86:111-152.

[7]Enochs E E,Jenda O M G.Relative Homological Algebra[M].Berlin:Walter de Gruyter,2000.

The balanced pair and complete cotorsion pair

Sun Dan,Yang Xiaoyan
(College of Mathematics and Statistics,Northwest Normal University,Lanzhou 730070,China)

This paper discuss the relationship of the balanced pair,special approximation relative to balanced pair and cotorsion pair relative to balanced pair,then give some properties about them,and get some equivalent characterizations of a relative complete cotorsion pair.

balanced pair,relative special approximation,relative cotorsion pair

O153.3

A

1008-5513(2017)02-0197-07

10.3969/j.issn.1008-5513.2017.02.011

2016-12-23.

国家自然科学基金(11361051).

孙丹(1992-),硕士生,研究方向：同调理论.

2010 MSC:16D10