六维Heisenberg李超代数的Yang-Baxter方程

郎爽,刘文德

(哈尔滨师范大学数学系,黑龙江 哈尔滨 150025)

六维Heisenberg李超代数的Yang-Baxter方程

郎爽,刘文德

(哈尔滨师范大学数学系,黑龙江 哈尔滨 150025)

利用六维Heisenberg李超代数的分类,在特征0的代数闭域F上通过计算刻画了六维Heisenberg李超代数Yang-Baxter方程所有的解.

Heisenberg李超代数;Rota-Baxter算子;Yang-Baxter方程

1 引言

Rota-Baxter代数由一个结合代数和一个线性算子组成,Rota-Baxter代数在物理,数论,组合等方面的应用越发广泛[1].Rota-Baxter算子是G.Baxter在研究波动理论时引入的,这个线性算子满足微积分中的分部积分公式中的等式[2].这个算子可推广到非结合代数中.近年来,许多人刻画了低维代数上的Rota-Baxter算子,例如文献[3-4]分别刻画了低维Pre-Lie代数上的Rota-Baxter算子,文献[5]刻画了有限维Hamilton结合代数和三、四维Heisenberg李超代数上的所有Rota-Baxter算子,文献[6]刻画出了三维幂零李超代数的Yang-Baxter算子,文献[7]刻画了五维Heisenberg李超代数上的Rota-Baxter算子.

本文根据6维Heisenberg李超代数在特征0的代数闭域F上的分类[8],通过计算刻画出了6维Heisenberg李超代数的所有Yang-Baxter方程的解.约定N表示正整数集.As×t为F上任意s×t阶矩阵,其中s,t∈N.

2 基本概念

定义 2.1设L为域F上的李超代数[9],λ∈F.若R:L→L是齐次线性算子,并且满足

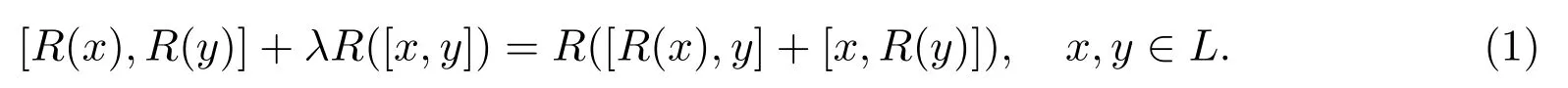
则称R是李超代数上权为λ的Rota-Baxter算子.当R次数是偶数时,称为偶算子,当R次数是奇数时,称为奇算子.特别地,λ=0时,(1)式称为经典Yang-Baxter方程.

定义2.2[10]设H是域F上的有限维李超代数,若H满足 [H,H]=Z(H),dimZ(H)=1,则称H为Heisenberg李超代数.

Heisenberg李超代数g按中心元素z的奇偶性,其中z是Z(H)中的非零元,可分为如下两类:

(1)若|z|=0,则g具有齐次基u1,···,um,v1,···,vm,z,w1,···,wn,其中

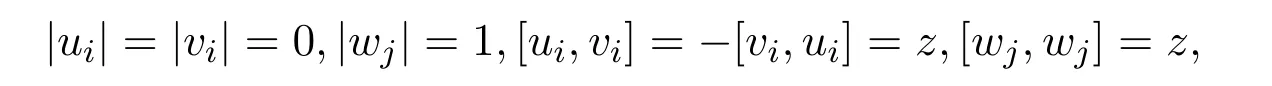
其余李积为0,此时用gm,n表示.

(2)若|z|=1,则g具有齐次基u1,···,un,z,w1,···,wn其中

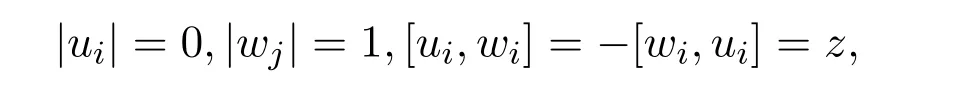
其余李积为0,此时用gn表示.

因此,六维Heisenberg李超代数同构于以下三种代数之一[8]:

(1)|z|=0,g2,3具有齐次基u1,v1,z,w1,w2,w3,乘法表为

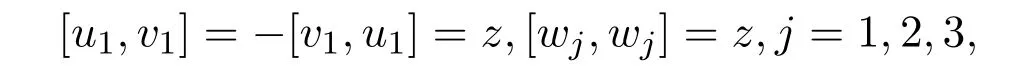
其余李积为0;

(2)|z|=0,g4,1具有齐次基u1,u2,v1,v2,z,w1,乘法表为

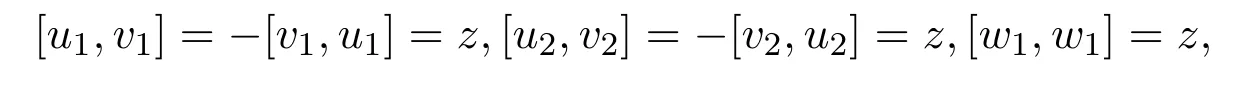
其余李积为0;

(3)|z|=0,g0,5具有齐次基z,w1,w2,w3,w4,w5,乘法表为[wj,wj]=z,j=1,···,5,其余李积为0.

现将g上的Rota-Baxter算子R分别写成在上述基下的矩阵,形式为(rij),本文将计算权0的Rota-Baxter算子在各组基下的矩阵.

3 主要结果

定理 3.1Heisenberg李超代数g2,3的偶Yang-Baxter方程的解为

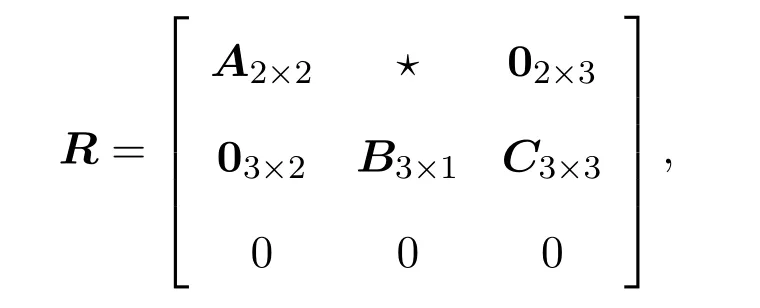
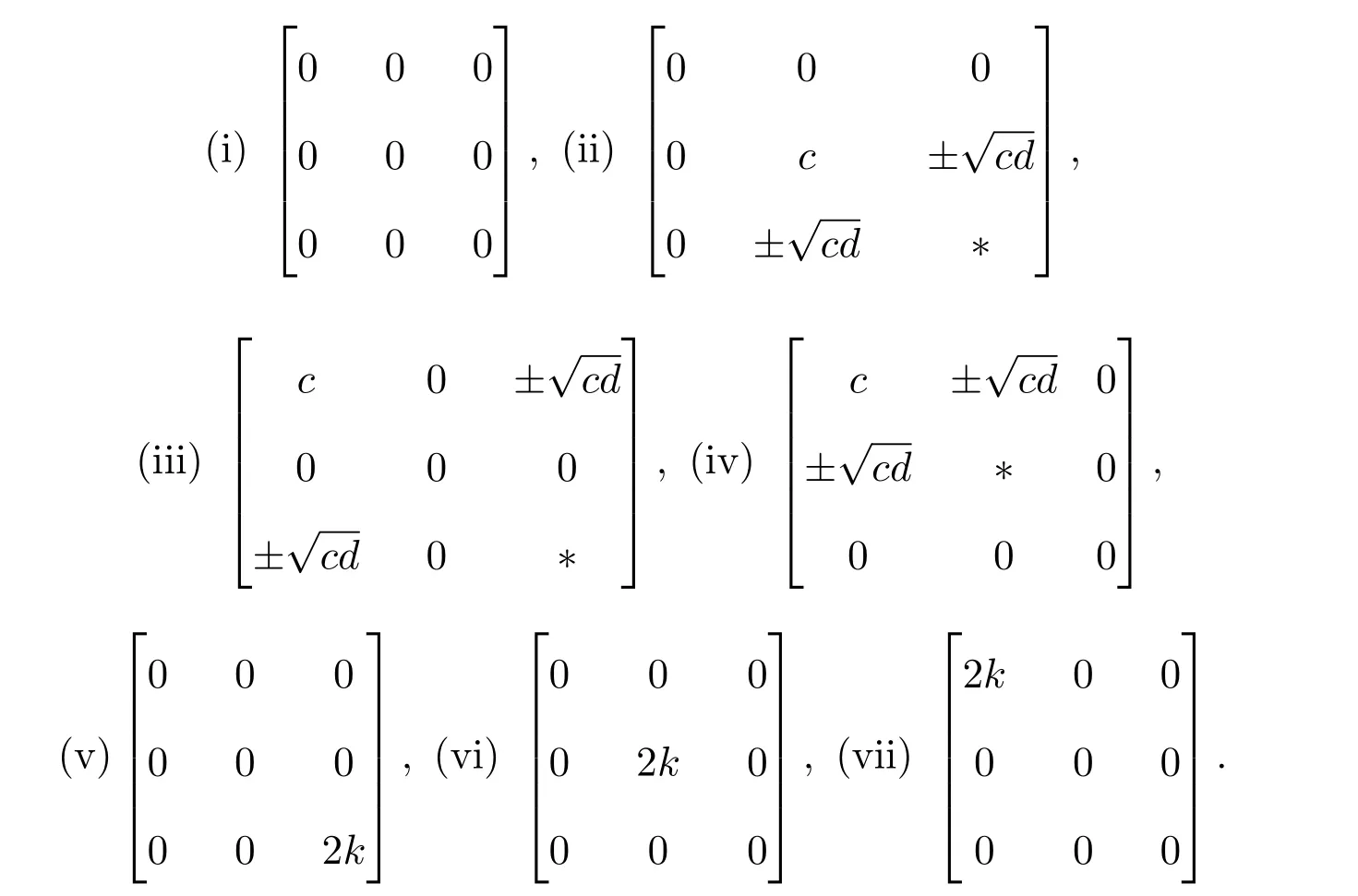
A有两种情况,分别为:

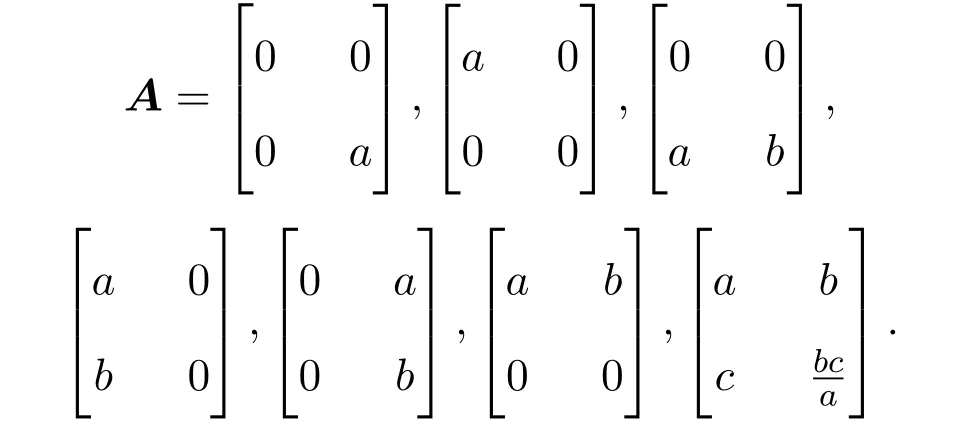
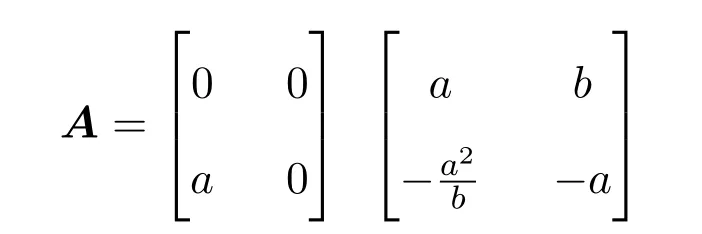
a,b,c,k∈F,d=2k−c,∗=c或d.

证明由于R为偶的线性算子,可设

当λ=0的情形,由于R为线性的,故只需考虑基元素满足(1)式,从而有r13,r23是任意的以及下面等式成立:

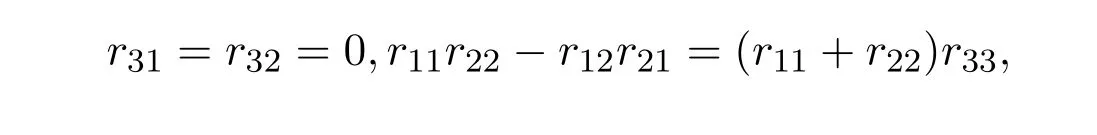
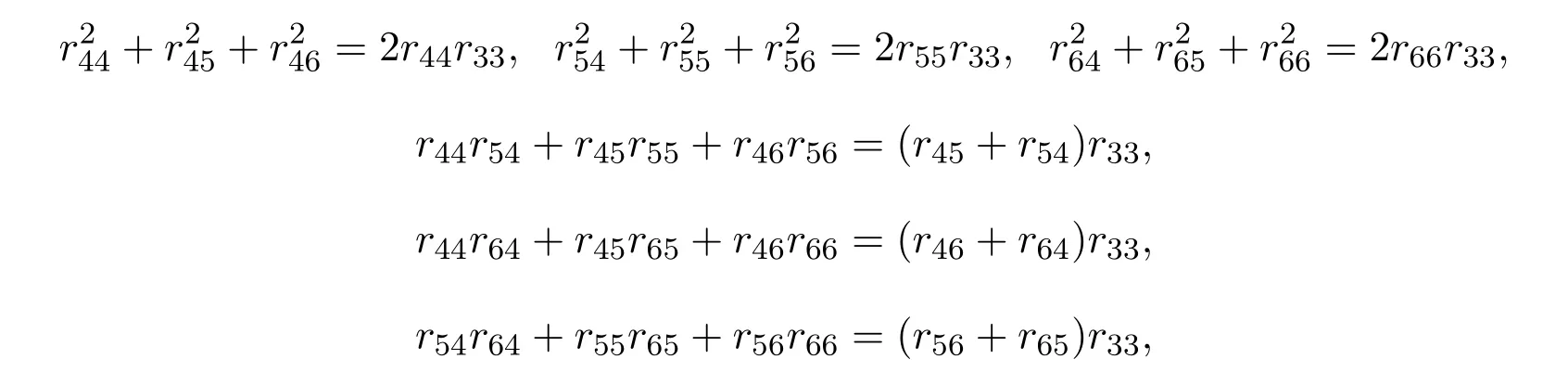
再分两种情况讨论:r11+r22=0和r11+r220,经计算可得.

定理 3.2Heisenberg李超代数g2,3的奇Yang-Baxter方程的解为

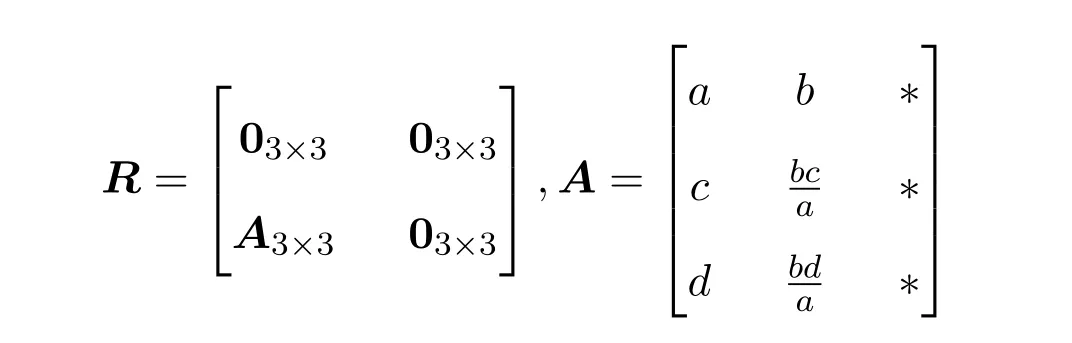
a,b,c,d∈F.

证明由于R为奇的线性算子,可设

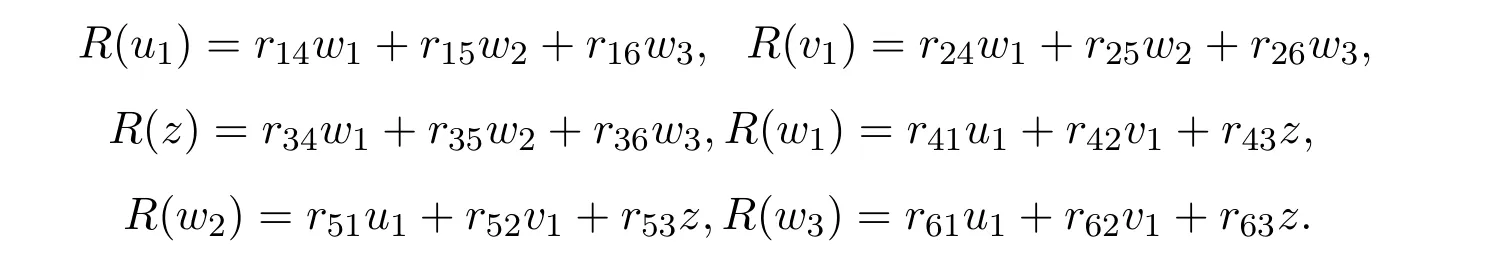
当λ=0的情形,根据R满足(1)式

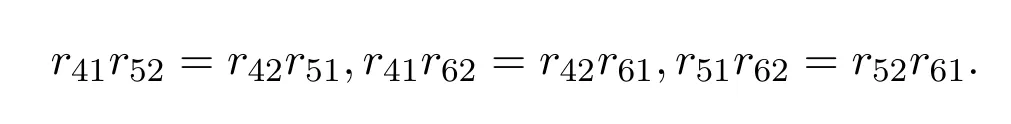
经计算可得.

定理 3.3Heisenberg李超代数g4,1偶Yang-Baxter方程的解为

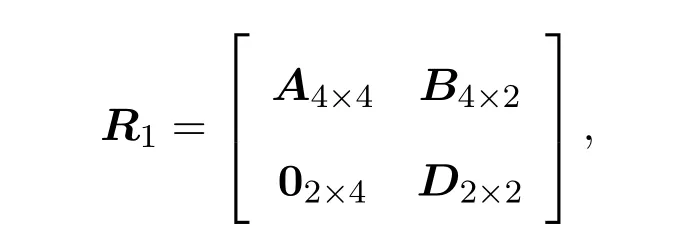
其中

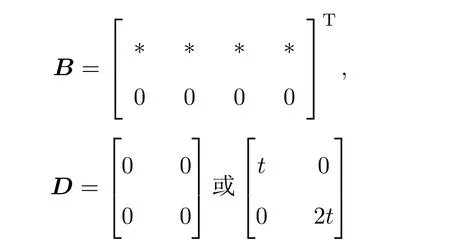
矩阵A中元素与D有关.

奇Yang-Baxter方程的解为

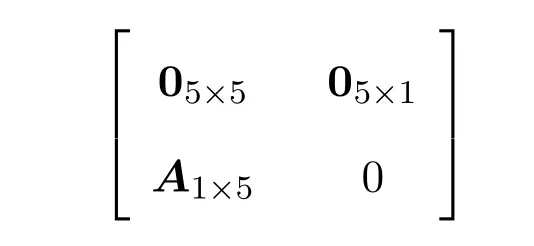
其中A任意.

定理 3.4Heisenberg李超代数g4,1偶Yang-Baxter方程的解为

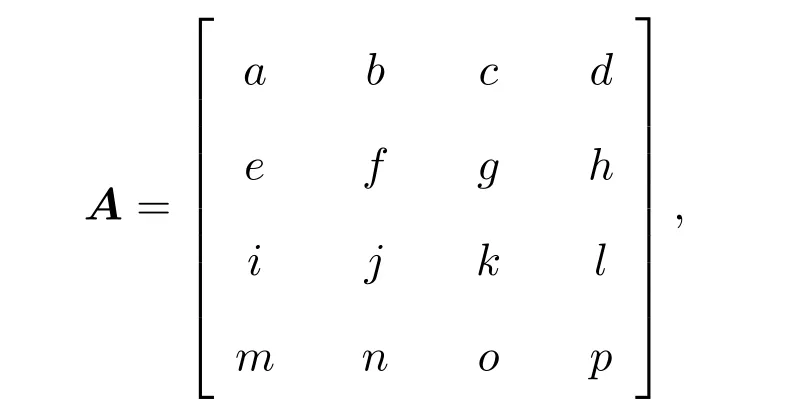
A中元素关系为以下两种之一:

(1)当

时,

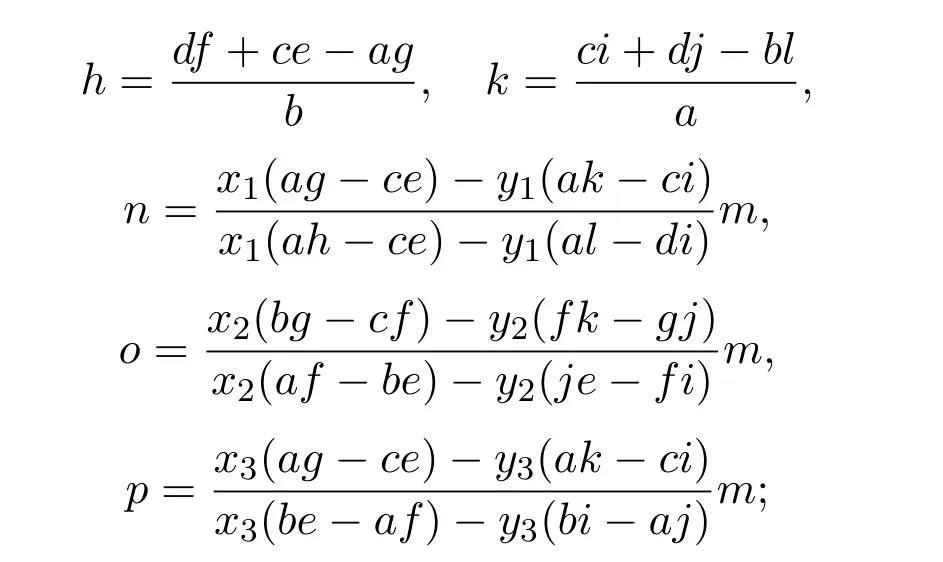
其中

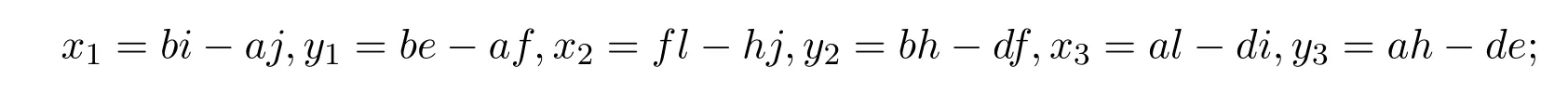
(2)当

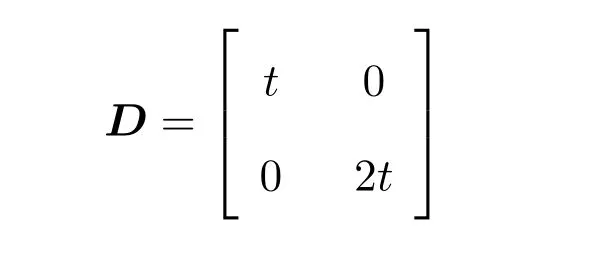
时,

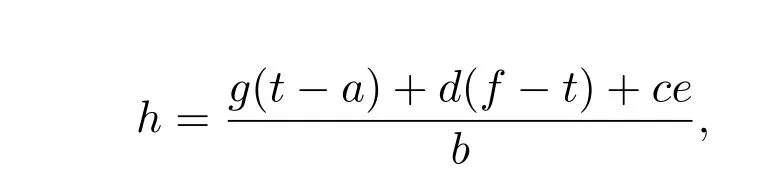
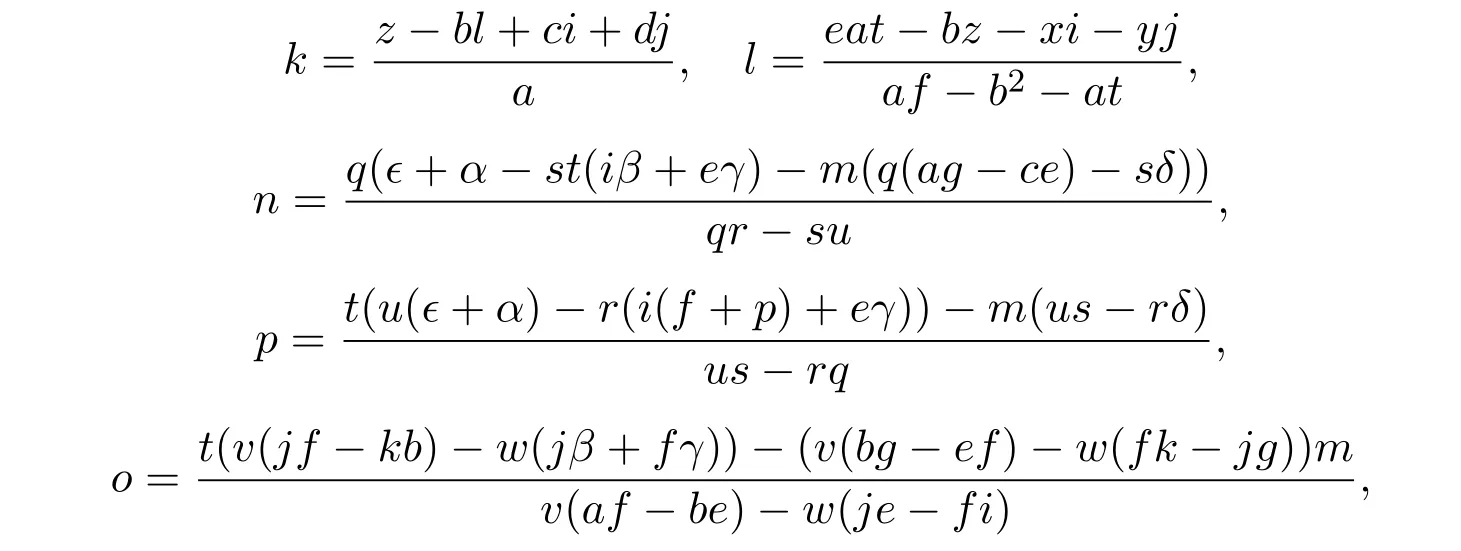
其中

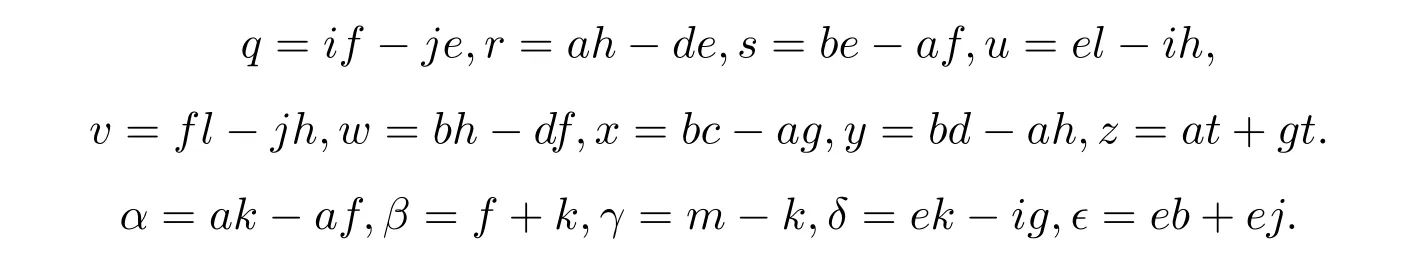
证明由于R为偶的线性算子,可设

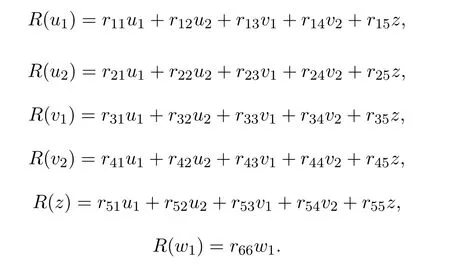
λ=0的情形,根据R满足(1)式可得

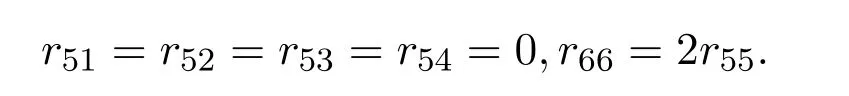
R为奇的线性算子时,可设

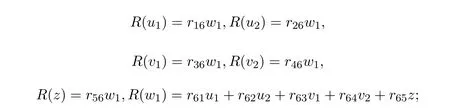
λ=0可得

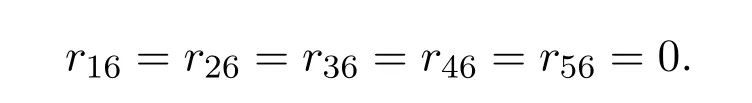
经计算可得定理3.4的结果.

表1 g0,5偶的Yang-Baxter方程的解

定理3.5Heisenberg李超代数g0,5偶的Rota-Baxter方程的解为Ri(i=1,···,5),则如下表：

证明由于R为偶的线性算子,可设

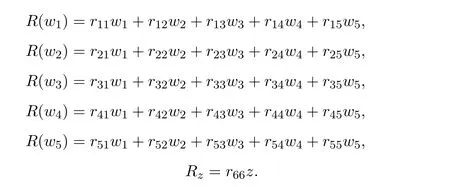
根据R满足(1)式,分两种情况讨论:

(1)r66=0;(2)r660.

在情况(1)中,分五种情况讨论:

(a)r11=0,(b)r22=0,(c)r33=0,(d)r44=0,(e)r55=0.

经计算可得定理3.5的结果.

定理 3.6Heisenberg李超代数g0,5奇的Yang-Baxter方程的解为

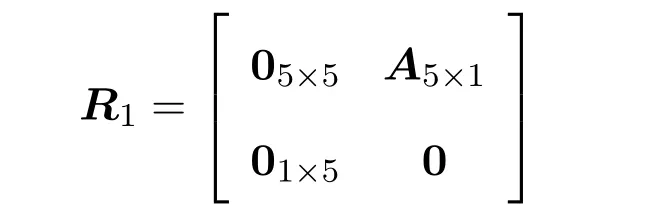
其中A任意.

证明同定理3.3.

[1]Guo L.An Introduction to Rota-Baxter Algebra[M].北京：高等教育出版社,2012.

[2]G Baxter.An analytic problem whose solution follows from a simple algebraic[J].Pacific Journal of Mathematics,1960,10(3):731-742.

[3]Li X X,Hou D P,Bai C M.Rota-Baxter operators on pre-Lie algebras[J].Journal of Nonlinear Mathematical Physics,2007,14(2):269-289.

[4]An H H,Bai C M.From Rota-Baxter algebras to pre-Lie algebras[J].Journal of Physics A Mathematical &Theoretical,2008,41(1):1-19.

[5]温雅慧.Hamilton代数和Heisenberg超代数上Rota-Baxter算子[D].哈尔滨:哈尔滨师范大学,2014.

[6]顾金剑,刘文德.三维幂零李超代数的Yang-Baxter算子[J].纯粹数学与应用数学,2014,30(3):307-313.

[7]吕思琦,刘文德.五维Heisenberg李超代数的Rota-Baxter算子[J].数学的实践与认识,2016,20:248-258.

[8]Rodr í guez-Vallarte M C,Salgado G,S á nchez-Valenzuela O A.Heisenberg Lie superalgebras and their invariant superorthogonal and supersymplectic forms[J].Journal of Algebra,2011,332(1):71-86.

[9]Kac V G.Lie Superalgebras[J].Advances in Mathematics,1977,26:8-96.

[10]Liu W D,Chen M W.The minimal dimensional of faithful representations for Heisenberg Lie superalgebras[J].Journal of Geometry&Physics,2015,89:17-23.

Rota-Baxter operators on Heisenberg Lie superalgebras of dimension six

Lang Shuang,Liu Wende
(Department of Mathematics,Harbin Normal University,Harbin 150025,China)

According to the classification method of Heisenberg Lie superalgebras,we characterize all solutions of the Yang-Baxter equations of the six dimensional Heisenberg Lie superalgebras g2,3,g4,1and g0,5over algebraically closed fields of characteristic 0.

Heisenberg Lie superalgebra,Rota-Baxter operator,Yang-Baxter equation

O152.5

A

1008-5513(2017)02-0177-08

10.3969/j.issn.1008-5513.2017.02.009

2016-12-30.

国家自然科学基金(11471090).

郎爽(1995-),硕士生,研究方向：李代数与李超代数.

刘文德(1965-),博士,教授,研究方向：李代数与李超代数.

2010 MSC:17B05