分光棱镜位置变化对自准直测角光管角度测量误差的影响

王学根，孙 煜，贺永喜

（北京航天发射技术研究所，北京，100076）

分光棱镜位置变化对自准直测角光管角度测量误差的影响

王学根，孙 煜，贺永喜

（北京航天发射技术研究所，北京，100076）

采用矢量分析的方法从理论上推导出分光棱镜位置变化对目标返回光线的影响，进而分析出其对自准直测角光管中目标像点位置的影响，并给出位置变化对角度测量误差的影响关系式，对自准直测角光管等精密仪器中分光棱镜安装座设计提出建议。

分光棱镜；位置变化；矢量法；角度测量；误差

0 引 言

分光棱镜是自准直测角光管光路设计中的关键部件，其主要作用是通过内反射的方式改变被测目标的反射光线，使其偏离光学系统光轴方向一定角度（一般为 90°），在空间上方便安装电荷耦合元件（Charge-coupled Device，CCD）等光电器件以实现光电测量，自准直测角光管光路原理如图1所示[1]。作为一种精密的角度测量设备，自准直测角光管的测角精度比较高，通常试验室内能达到0.5～0.1″。对于军用高精度的自准直测角光管，测角精度绝对值的高低不是其唯一考核的指标；其在全温域（温度环境一般为-40～60 ℃）范围内，测角精度的稳定性则更重要。在上述宽温范围内，分析自准直测角光管误差源，分光棱镜的制造和安装稳定性误差不可小视。因为经分光棱镜反射的目标光线是测量被测目标方位信息的载体，分光棱镜本身的制造误差及其安装稳定性误差将直接影响测量精度。本文不讨论分光棱镜的制造误差对测量精度的影响[2]，仅关注其安装稳定性误差给测量精度带来的可能影响。根据光线的反射定律及转动定理，结合分光棱镜安装的误差源形式，本文采用矢量分析的方法从理论上推导出安装位置变化对目标返回光线成像位置变化的影响关系，进而分析出其对测量误差的影响，并对分光棱镜安装座的设计提出建议。

图1 自准直测角光管光路原理

由图1可知，分光棱镜的分光面是一个平面镜，利用平面镜反射实现测量光束偏转90°，为安装CCD器件提供空间并实现光电测量。

1 平面镜反射定律的矢量法表示

平面镜反射矢量示意如图2所示。

图2 平面镜反射矢量示意

图2中，A为入射光线单位矢量，N为反射面法线的单位矢量，A′为A的反射光线单位矢量，由矢量三角形O12得反射矢量公式[3]如下：

设A，N，A′在坐标系XYZ上的分量分别为 AX， AY， AZ，NX， NY， NZ， A′X， AY′， AZ′，代入式（1），得：

将式（2）写成矩阵形式：

式中R为平面镜的反射作用矩阵，其中：

2 转动矢量公式

矢量A绕转轴单位矢量P转动一角度θ而成为矢量A′，其转动矢量表达式[4]为

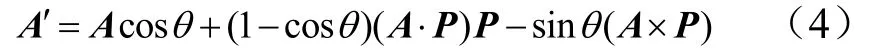
将式（4）写成矩阵形式：

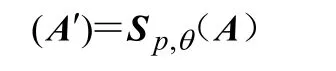
Sp,θ代表绕P转θ角的转动矩阵：

式中 PX，PY，PZ分别为单位转轴矢量P在X，Y，Z方向的分量；θ为矢量A绕转轴P转动的角度。在特殊情况下，P与坐标系XYZ中的某一个坐标轴重合。此时，转动矩阵S,iθ，Sjθ,和S,kθ分别为

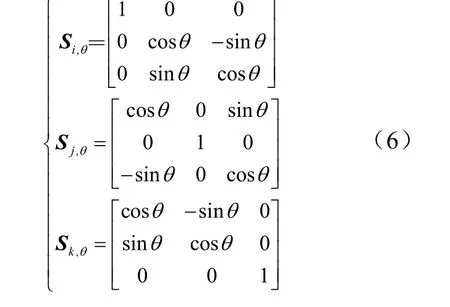
3 分光棱镜位置变化对反射光线的影响[5]

分光棱镜安装后的任一位置变化可以表示为在空间坐标系3个坐标轴方向的投影分量，即在X，Y，Z坐标轴方向的位移误差分量XΔ， YΔ， ZΔ 及绕X，Y，Z坐标轴的转动误差分量ΔθX，ΔθY，ΔθZ。由于分光棱镜在X，Y，Z坐标轴方向的位移XΔ，YΔ， ZΔ 仅影响入射光线在分光棱镜上的反射作用点，而不会影响反射光线的方位，所以其对测量精度的影响可以不考虑。因此分光棱镜安装后的位置变化仅考虑其绕X，Y，Z坐标轴的转动量ΔθX，ΔθY，ΔθZ。

下面分别讨论分光棱镜安装后其绕X，Y，Z坐标轴的转动分量ΔθX，ΔθY，ΔθZ对反射光线的影响，见图3。

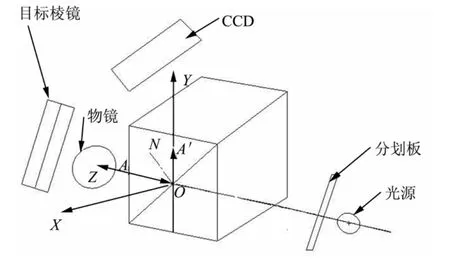
图3 分光棱镜内反射工作示意

由图3可知，被目标棱镜反射回光学系统的光线为A′，其相对于分光棱镜反射面为入射光线。用图 3中所示的光学系统坐标系表示，入射光线的单位矢量表示为，当入射光线A与分光棱镜反射面法线呈 45°角时，分光棱镜反射面法线的单位矢量为，反射光线单位矢量为，此时的分光棱镜位置为理想位置。

3.1 分光棱镜绕X轴转动XθΔ对反射光线的影响

分光棱镜绕X轴转动ΔθX后，其反射面的法线为

式中,iθΔS为转动作用矩阵，。将其代入式（7）得：

将式（8）代入式（3）得反射面的作用矩阵RθX：

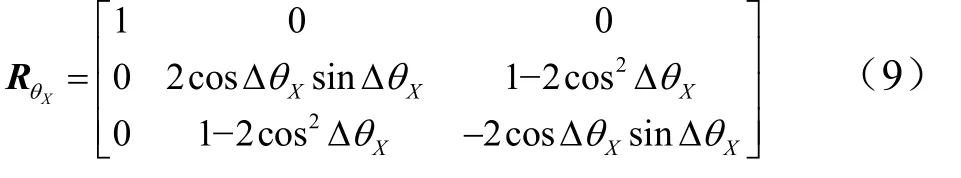
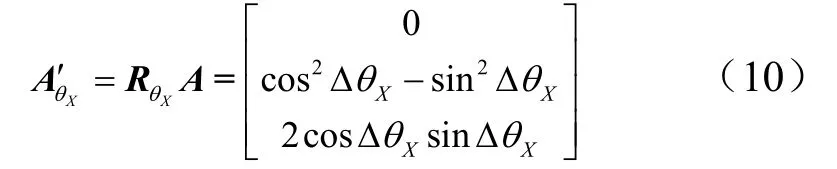
3.2 光棱镜绕Y轴转动YθΔ对反射光线的影响

按照3.1节的步骤，同理可得分光棱镜绕Y轴转动ΔθY后的反射光线为

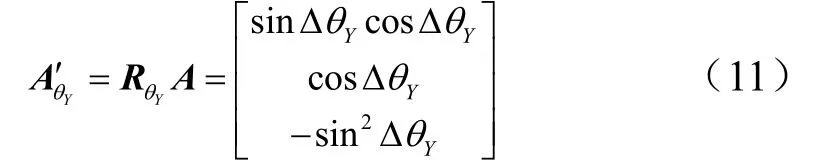
3.3 分光棱镜绕Z轴转动ZθΔ对反射光线的影响

3.4 影响分析[6,7]

在图3中，反射光线在X，Y，Z 3个坐标轴方向的分量变化将最终影响返回光线的成像位置。但由于测量敏感方位是X轴方向，即X轴方向的变化将作为测量误差直接带入测量结果。根据3.1～3.3节的计算结果可得分光棱镜分别绕X，Y，Z轴转动后引起的成像位置变化，结果如表1所示。

表1 分光棱镜位置变化与相应的成像位置关系

由表1可知：

a）分光棱镜绕X轴转动，反射光线在X轴无变化，因此不会引入方位测量误差；

b）分光棱镜绕Y轴转动YθΔ，引入方位测量误差为，根据图4（函数y=(θ-sin(θ))×180×3600/π的图像）可知[8]：当ΔθY≤0.015 rad时,λY≈ΔθY（其中，λY单位为rad）；

c）分光棱镜绕Z轴转动ΔθZ，引入方位测量误差为λZ=-sin ΔθZ，根据图4（函数y=（θ-sinθ）×180×3600/π的图像）可知：当ΔθZ≤0.03 rad时，λZ≈-ΔθZ；

d）分光棱镜绕Y,Z轴的小角度（绕Y轴不大于0.015 rad，绕Z轴不大于 0.03 rad）转动，将按 1∶1的比例引入方位误差，因此要严格控制分光棱镜绕Y、Z轴的转动位置变化；

e）分光棱镜绕X，Y轴转动，成像位置在Z轴方向有变化，针对线阵CCD器件，成像点在沿X轴敏感阵列的垂向有位移，这种变化的带来的可能影响如下：

1）由于像点形状不是理想的轴对称图形，其成像位置在 CCD敏感阵列垂向的变化可能引入采集像点部位发生变化，从而带来测量误差；

2）当像点位移大时，可能使像点位置脱离 CCD敏感阵列，造成CCD测量功能失效。

f）分光棱镜绕X，Y，Z轴转动，成像位置在Y轴都有变化，根据其值的大小分析，成像位置都远离了想焦面位置，这种离焦现象会影响目标返回像在CCD敏感面的成像质量；

g）分光棱镜装调时其安装位置与理想位置的小量误差对自准直测角光管测量的影响可以通过装调、标定来消除，一般不会影响自准直测角光管的测量精度；

h）自准直测角光管在使用过程中由于温度、振动、冲击等工作环境造成的分光棱镜位置变化引入的上述误差无法消除，其大小不可忽视，最终会影响自准直测角光管的环境适应性能。

图4 函数y=（θ-sinθ）×180×3600/π的图像

4 结 论

自准直测角光管使用过程中，工作环境的温度、振动、冲击等应力因素造成的分光棱镜绕X，Y，Z轴转动方向的位置变化会给测量带来误差。为减小或消除这一误差源，根本的方法是自准直测角光管在使用过程中保持分光棱镜的位置不变。为实现这一目标，分光棱镜座的设计及分光棱镜组件的装配应考虑以下几点：

a）分光棱镜座易做成绕Y，X轴对称结构，使其产生的变形均匀对称；

b）分光棱镜座的Y，Z方向刚度要大些，使分光棱镜绕Y，Z转动的位置变化尽量小；

c）分光棱镜座与分光棱镜作为一个整体装配在自准直测角光管中，受力应均匀对称，且在外力作用下分光棱镜应趋向于稳定状态。

[1]李晓彤. 几何光学和光学设计[M]. 杭州: 浙江大学出版社, 1997.

[2]王之江, 等. 光学技术手册[M]. 北京: 机械工业出版社, 1994.

[3]匡萃方, 等. 用矢量方法分析角锥棱镜直角误差对其反射光路特性的影响[J]. 光学仪器, 2004, 25(4):55-58.

[4]王骏, 等. 一种直角棱镜棱脊相对变化量测量方法[J]. 科学技术与工程, 2006, 6(18): 2880-2886.

[5]尚鸿雁. 激光自准直测角系统安装误差分析[J]. 应用激光, 2008, 28(4): 318-322.

[6]高立民, 等. 直角棱镜棱镜倾斜对方位瞄准的影响[J]. 光子学报, 2002, 31(1): 117-119.

[7]欧同庚, 等. CCD光电自准直仪工作原理及误差源分析[J]. 大地测量与地球动力学, 2007(6): 98-100.

[8]张铮, 等. MATLAB程序设计与实例应用[M]. 北京: 中国铁道出版社, 2003.

Influence on Autocollimation Angle Measuring Caused by Motion of Beam Splitting Prism

Wang Xue-gen, Sun Yu, He Yong-xi
(Beijing Institute of Space Launch Technology, Beijing, 100076)

The influence on reflection beam from the target caused by the motion of beam splitting prism is theoretically deduced, with vector analyzing method. The affection on the postion of the target image for autocollimation measuring is analysed further. The relation between the angle measuring error and the motion of the target image is given. Some advices for the design of prism seat are given, which is used in the precision equment as well as the autocollimation.

Beam splitting prism; Motion; Vector method; Angle measuring; Error

TH741

A

1004-7182(2017)01-0022-04

10.7654/j.issn.1004-7182.20170106

2016-05-24；

2016-10-08

王学根（1976-），男，高级工程师，主要研究方向为光电测量及精密仪器