基于分解策略的SSO任务发射轨道优化研究

胡冬生，王俊峰，张普卓

（1. 中国运载火箭技术研究院研究发展中心，北京，100076；2. 北京宇航系统工程研究所，北京，100076）

基于分解策略的SSO任务发射轨道优化研究

胡冬生1，王俊峰2，张普卓2

（1. 中国运载火箭技术研究院研究发展中心，北京，100076；2. 北京宇航系统工程研究所，北京，100076）

700 km太阳同步轨道为运载火箭弹道设计中典型的发射任务。采用轨迹分解优化策略对此类任务的发射轨道进行研究，分析了中间轨道近地点高度、入轨点真近点角两个约束变量对火箭运载能力的影响，并重点结合气动热流限制对约束变量的取值进行了计算分析。采用的研究思路和得出的结论对于运载火箭上升段弹道的优化设计以及提升运算收敛性和设计效率均有一定的意义。

分解优化策略；发射轨道；约束变量；气动热流

0 引 言

700 km太阳同步轨道（Sun Synchronous Orbit，SSO），广泛应用于地球资源勘察、气象/灾害监测、军事侦察等对地观测领域，很多情况下运载火箭的设计基于700 km SSO运载能力作为技术指标。对于该类发射任务，运载火箭上升段弹道往往采用有中间轨道的发射弹道，通过无动力滑行，利用重力来改变速度方向，进而提升火箭性能，解决火箭动力飞行时间短的问题[1,2]；如此带来设计变量的增多，弹道设计及优化复杂。火箭飞行过程包含上升段、中间无动力转移段和轨道圆化段，各个飞行段不同的弹道特性增强了整个问题的非线性，算法收敛变得更加困难[3]。在这类多轨迹段的弹道优化问题的求解上，轨迹分解优化策略是一种有效的手段。本文应用分解优化策略对SSO任务的发射轨道进行分析研究。

1 分解优化策略设计思路

1.1 分解优化策略概述

分解优化策略是将整个任务分为不同的飞行段，如上升段、再入段、滑行段等，每个飞行段通过设置不同的约束目标值产生一个满秩的子问题，可以应用迭代法求解。同时，这些子问题中的约束又作为主问题中的独立变量，结合整个问题的优化目标应用梯度投影法等算法对这些独立变量进行优化。在整个问题的求解中，第1级是各个子问题的迭代求解，第2级是主问题的优化。采用两级分解优化策略后，问题的收敛大大加快，提高了优化效率。

Petersen等应用两级轨迹分解算法对执行地球同步转移轨道（Geostationary transfer oribt，GTO）任务的火箭发射弹道进行了研究，将整个弹道分解为上升段、轨道转移段及轨道圆化段，并引入卫星质量、上升段关机速度及转移轨道倾角作为子问题的目标约束及主问题的独立变量，进而以运载能力为目标进行优化得到约束变量的值[3]；Beltracchi等应用分解策略对地球静止轨道（Geostationary Earth Orbit，GEO）任务开展分析，将整个弹道优化问题分解成助推级及上面级两个飞行段，以中间停泊轨道参数作为子问题的目标约束（近地点高度、远地点高度和近地点辐角），对子问题和主问题均开展优化运算，通过优化停泊轨道参数提升GEO任务的运载能力，同时针对停泊轨道参数对运载能力的灵敏度进行计算分析，以获得不同参数取值对运载能力的影响[4]。

1.2 SSO任务发射轨道分解策略设计模型

对于三级运载火箭（三级可二次启动）执行700 km SSO任务的弹道设计而言，其飞行过程为：火箭起飞至三级一次关机进入中间转移轨道，滑行一段时间后，在700 km高度左右二次点火进行轨道圆化，最终进入目标轨道。图1为运载火箭执行700 km SSO任务发射轨道示意。

图1 运载火箭执行700km SSO任务发射轨道示意

通常除了发射方位角可通过与轨道倾角的关系进行独立设计外，还有一级最大攻角αm、二级程序角斜率dφcx2、三级一次飞行段程序角斜率dφcx31、三级一次关机时间tk31、三级滑行时间tc、三级二次点火时刻程序角 φcx32、三级二次飞行段程序角斜率 dφcx32、三级二次工作时间tk32共8个设计变量，而目标约束仅有3个：700 km SSO入轨点的v，r，θ。设计变量个数远远多于约束个数。

一般情况下，三级二次工作时间较短，该段程序角斜率对结果影响很小，可认为该段按常值程序角飞行，即dφcx32=0。对于其余的设计变量，可以根据分解策略引入若干中间约束，将全飞行段分为3个小段，每个小段的设计变量与约束个数相等，从而应用迭代法求解方程组的方式来求出设计变量值。引入的3个约束分别为一级关机点当地弹道倾角 θk、中间轨道近地点高度hp及中间轨道入轨点位置f（即真近点角），运载能力仅与这3个参数有关，可表示成三者的函数。同时，添加了 1个不等式约束：末级剩余推进剂量mpr≥0 kg。因此，弹道优化的目的即为寻找一级关机点θk、中间轨道hp及入轨点f，使得火箭运载能力最大。尤其需要开展中间轨道 hp及入轨点 f对火箭弹道设计的影响，给出合理取值范围，以有效指导发射轨道的设计和优化。由此可将原问题转化为 1个主问题和 3个子问题，如图2所示。

图2 三级运载火箭执行SSO任务分解策略优化方法

1.3 仿真计算效果

以某三级液体运载火箭为例，进行弹道优化计算和分析。弹道计算中采用椭球形地球模型，考虑J2项引力摄动，所用弹道计算模型见文献[5]。

采用传统方法求解时，算法对初值的设置较为敏感，常出现运算发散需要修改初值并重新启动运行的情况，且在数十次迭代以内难以收敛。分解优化策略虽然增加了求解问题的数量，但每个子问题的求解均比较简单，且仅需迭代4次左右即可完成收敛，子问题的顺利求解加快了主问题的求解速度。相对而言，分解优化策略大大增加了求解的可靠性和鲁棒性[6]。

2 优化变量对火箭性能的影响分析

2.1 不同近地点高度及真近点角情况下的运载能力

为计算分析不同近地点高度及真近点角对运载能力的影响，分别计算近地点高度取值区间为20～250 km情况下，不同真近点角时（对应中间轨道不同入轨点）对应的运载能力。在每次计算中，暂不考虑落区约束，设定近地点高度及真近点角为固定值，优化一级关机点当地弹道倾角，使火箭运载能力最大。当近地点高度小于80 km时（含亚轨道），人为设定火箭进入中间轨道时高度应大于80 km，且在近地点以后入轨。

近地点高度为80～250 km情况下运载能力随真近点角变化曲线见图3。为便于比较，将计算出的运载能力统一除以某固定值，形成无量纲运载能力。

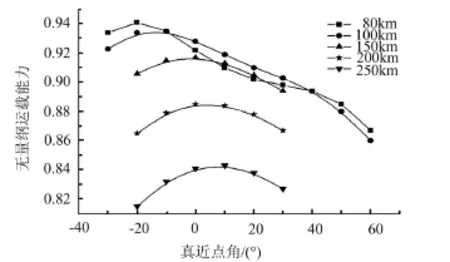
图3 不同近地点高度运载能力曲线

由图3可以看出：

a）运载能力随着近地点高度的降低而增加。近地点高度降低时，火箭飞行过程中的重力损失减小，有助于运载能力的提升。

b）对于相同近地点高度，真近点角的取值存在一个最优值，使得运载能力最大；该最优值位于近地点附近，且随着近地点高度的升高而增大（真近点角为负值表示火箭在近地点之前进入中间轨道）；近地点附近入轨可基本保证火箭按照霍曼变轨的方式实现轨道转移，在充分利用重力转弯改变速度方向的同时抬高飞行高度，从而达到性能优化。

c）对于图3的曲线簇，同一运载能力可能与不同曲线或同一曲线存在多个交点，因此可以通过设置不同近地点高度和真近点角组合来达到相同运载能力。

近地点高度为20～80 km情况下运载能力随真近点角变化曲线见图 4。此时，运载能力随真近点角的变化曲线与大于80 km时的情况不同，运载能力最优值出现在近地点以后入轨情况（对应真近点角40～60°）。可见，当近地点高度过小时，受到在近地点以后入轨及入轨高度的影响，火箭不能充分利用霍曼变轨来达到性能优化，运载能力反而大幅降低。因此，若对火箭在中间轨道的滑行时间以及测控条件没有约束，则应尽量避免采用近地点高度过低的中间轨道，尤其是亚轨道。

图4 不同近地点高度运载能力曲线（20～80km）

2.2 最低回落高度及气动热流变化情况

在弹道计算中，当中间轨道入轨点高度过低或入轨点弹道倾角过小时，火箭飞行弹道会出现一个“回落”的阶段。一方面，入轨点高度过低会造成入轨点速度变大，在各级推重比及发动机工作时间一定的情况下，火箭需通过拉低弹道来增大飞行速度；另一方面，入轨点弹道倾角为负值时，则必然需要通过飞行高度的压低来满足入轨要求。在弹道“回落”的阶段飞行高度有所降低，之后高度持续升高，因而存在一个“最低回落高度”。中间轨道近地点高度80 km、入轨点真近点角20°时火箭飞行高度随时间变化曲线见图5。

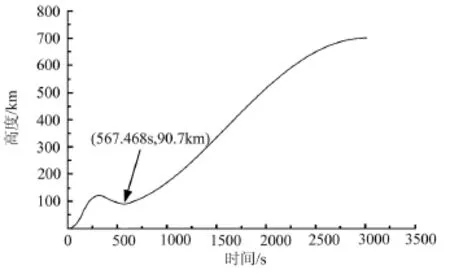
图5 飞行高度随时间变化曲线

由图5可以看出，最低回落高度出现在567.468 s、高度约90.7 km处。

高度回落带来的影响是：由于此时卫星整流罩已分离（整流罩一般在二级飞行段分离，分离高度约100～120 km之间），卫星裸露在外界空间，仍将受到稀薄大气的热流作用。高度降低后，大气密度增加，而同时火箭飞行速度相比整流罩分离时增大很多，这样就有可能使热流快速回升，对卫星产生不利影响。计算表明，在相同近地点高度情况下，真近点角越小，热流再次回升的值越大，卫星的飞行环境越恶劣。

在最低回落高度时刻，大气还具有一定密度，且火箭飞行速度始终在持续增大。根据热流计算公式，热流再次回升至最大点（可称为“最大回升热流”）往往在最低回落高度对应时间点之后。如在近地点高度80 km、真近点角20°，最大回升热流点在最低回落高度点之后8 s，如图6所示。

图6 火箭飞行热流曲线

为了将最大回升热流限制在卫星可承受的范围内（如不大于1 135 W/m2），需要将最低回落高度抬高至一定值，可通过增大真近点角来实现（其对应的真近点角可称为“临界真近点角”），或者抬高中间轨道近地点高度，计算结果见表1。表1表明，最低回落高度应不小于132 km，才能满足卫星热流要求，且运载能力随着近地点高度的增大而有所提升。对于近地点高度150 km以上的情况，最优运载能力在0°真近点角附近，此时高度回落及热流回升均不明显，均能满足卫星热流约束。

表1 不同近地点高度对应的临界真近点角及相关参数

2.3 近地点高度及真近点角的选择

为了满足热流限制，最低回落高度应不小于一定值（如132 km），则应对近地点高度及真近点角的取值做一定限制。结合前面计算结果，可根据中间轨道近地点高度分两种情况进行讨论：

a）近地点高度低于150 km（含亚轨道）。

若考虑热流约束，则运载能力相比2.1节中的最优值将有不同程度的降低。以近地点高度80 km为例，运载能力将由最优值0.941降至0.892以下，甚至小于近地点高度 150 km、真近点角为 0°时的运载能力0.917。

b）近地点高度高于150 km。

在近地点入轨基本可保证运载能力最大，且最低回落高度不至于过低、回升热流不至于过大。当近地点高度为150 km时，回升热流在800 W/m2以下。

根据上述计算及分析，考虑热流因素后，较低近地点高度对应的运载能力可以由较高近地点高度、近地点附近入轨（即真近点角约为0°）来实现，甚至获得更大的运载能力。针对本文所提及的火箭构型，考虑一定余量后，近地点高度选取200 km左右为宜，过高或过低，都将带来运载能力的损失。

可见，近地点高度与真近点角的选择是一个综合权衡的过程，不能仅仅局限于运载能力的考虑给出一个最优值，因此该类弹道优化问题不存在所谓绝对最优值。工程设计中只能依据物理规律及各项约束条件选取一个大概的范围，该取值能使问题的求解得到简化，提高设计效率、满足设计要求，同时又不至于改变问题的本质，火箭性能不至于大幅降低。

3 结 论

应用分解优化策略对700 km SSO任务的发射轨道进行研究，提出一种求解弹道优化问题的思路，可较大程度上加快计算的收敛，提高计算鲁棒性和设计效率，并对类似的其它弹道设计问题均有借鉴价值。

重点分析了近地点高度、入轨点真近点角两个中间约束变量对运载能力的影响，并结合气动热流限制得出了一些定性及定量的结论，对于SSO任务发射轨道设计具有一定的意义：

a）设置不同的中间轨道近地点高度及入轨点真近点角，可得到相同运载能力，在弹道设计时应综合考虑气动热流等其它约束条件来确定设计变量取值。

b）中间轨道采用霍曼变轨方式使火箭运载能力得到较大提升，且近地点高度越低，对运载能力的提升越有利。但当近地点高度降低至一定值时，将使卫星受到严重的热流作用，对卫星产生不利的影响。

c）中间轨道近地点高度设置在200 km左右，并在近地点入轨，可基本兼顾运载能力优化及热流等约束。

应注意的是，文中给出的优化结果会随着运载火箭总体参数的不同而有所差异。在工程应用中，应根据测控、末级滑行时间、落区等实际情况综合权衡，在满足各项约束的前提下来考虑目标的优化，以选择合适的中间轨道设计变量值。

[1]Arianspace. VEGA User’s Manual[M]. Paris: Programmes Division Technical Service, 2002.

[2]The Boeing Company. DELTA Ⅳ payload planners guide[M]. California: Space and Communications Group, 2000.

[3]Petersen F M, Cornick D E, and Brauer G L. A two-level trajectory decomposition algorithm featuring optimal intermedia target selection[J]. Journal of Spacecraft and Rockets, 1977，14(11): 676-682.

[4]Beltracchi T J. Decomposition approach to solving the all-up trajectory optimization problem[J]. Journal of Guidance, Control, and Dynamics, 1992, 15(3): 707-716.

[5]贾沛然, 陈克俊, 何力. 远程火箭弹道学[M]. 长沙：国防科技大学出版社, 2004.

[6]Brauer G L, Cornick D E, Stevenson R. Capabilities and applications of the Program to optimize simulated trajectories program (POST) program summary document[R]. NASA CR-2770, 1977.

Launch Trajectory Optimization for SSO Mission Based on Decomposition Algorithm

Hu Dong-sheng1, Wang Jun-feng2, Zhang Pu-zhuo2
(1. R&D Center, China Academy of Launch Vehicle Technology, Beijing, 100076; 2. Beijing Institute of Astronautical Systems Engineering, Beijing, 100076)

In this paper the decomposition algorithm is proposed for the launch trajectory optimization of the SSO mission. The simulation is conducted to analyze the influence of two constraint variables to launch capability, such as perigee altitude and injection true anomaly of the intermediate orbit. Lastly, the value of the constraint variables is studied according to aerodynamic heating limitation. The research method and analysis results are important to trajectory optimization of launch vehicle, as well as the convergence of calculation and design efficiency.

Decomposition algorithm; Launch trajectory; Constraint variables; Aerodynamic heating

V412.4

A

1004-7182(2017)01-0010-05

10.7654/j.issn.1004-7182.20170103

2015-04-16；

2015-08-20

胡冬生（1982-），男，高级工程师，主要研究方向为运载火箭弹道设计