注重逻辑推理关注思维发展——由一道中考题的错解分析与多解思路引发的思考

☉浙江湖州市南浔区教育教学研究和培训中心姜晓翔

注重逻辑推理关注思维发展
——由一道中考题的错解分析与多解思路引发的思考

☉浙江湖州市南浔区教育教学研究和培训中心姜晓翔

中考试卷中的简单基础题能暴露学生的典型错误及多解思路，对今后的教学必然会产生一定的导向作用.基于此，笔者对2016年湖州市中考第20题进行研究，并在集中网评阅卷时特地进行了关注，现整理成文，与同仁分享.

一、原题呈现

（2016年湖州市第20题）如图1，已知四边形ABCD内接于圆O，连接BD，∠BAD=105°，∠DBC=75°.

（1）求证：BD=CD；

（2）若圆O的半径为3，求B（C的长.

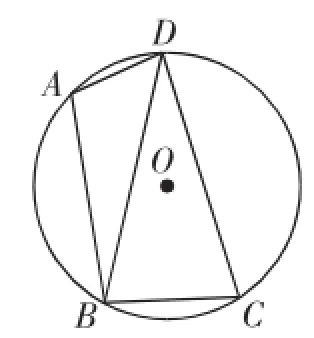
图1

二、试题总体评析

该题涉及的主要知识点有：圆内接四边形的性质、圆心角定理、圆周角定理、弧长的计算等.主要涉及的基本方法能力有：线段、弧、圆周角之间相等关系的转化，弧长公式的运用等，考查学生对基础几何问题的逻辑推理、规范书写及简单计算等基础能力.本题虽为一道基础简单的几何证明计算题，涉及的知识点也并不繁杂，但是从最后的阅卷报告发现，满分为8分的试题，实际平均得分才5.9分，得分率仅为0.74.由此可见，学生对于这类几何逻辑推理题的掌握并不理想，部分学生的书写过程缺乏规范性，与此同时，也涌现出了不同的解题思路，大致情况如下所示.

三、典型错误及其分析

该题的前两小题要求学生写出完整的解答过程，考查学生几何推理表达的能力.笔者将主要典型错误归类如下.

1.第（1）小题的典型错误及分析.

错解一：把∠ADC直接当直角用，然后证出结论BD=CD.

错解二：直接认为∠ABC=∠BAD=105°，然后证出结论BD=CD.

【分析】这两种错解主要原因是学生未审清题意，盲目地直观判断造成的.题目的条件并未指出∠ADC是直角或∠ABC=∠BAD=105°，学生却根据图形做出了直观的错误判断，由这些错误判断推理得出结论.相当于将原来条件一般化变为了特殊化，这是几何推理中较为容易犯的错误“直观看，缺推理”.

错解三：作DE⊥BC，经过点O.如图2，由垂径定理，得BE=CE，则BD=CD.

错解四：连接OB、OC、OD，直接得到∠ODB=∠ODC=15°，然后得到△DOB≅△DOC；则BD=CD.

【分析】错解三和错解四均属于

“辅助线满足过多条件”，其本质为“造条件”.错解三中作DE⊥BC，一定经过点O吗？即使经过也需证明.错解四中连接OB、OC、OD后，就有∠ODB=∠ODC=15°吗？就算有，也需要证明.在几何推理证明时，这样的典型错误属于“造条件，缺推理”.

2.第（2）小题的典型错误及分析.

错解一：把∠CDB=30°直接当成圆心角代入弧长公式算出错误结果.

错解二：弧长公式记错，或和扇形面积公式混淆，从而得出一个错误的结果.

【分析】第（2）小题的错解一和错解二，均因对弧长公式不理解所造成.错解一是将公式中的圆心角用题中的圆周角所代替，错解二则完全记错公式，这两种典型错误原本为最低级错误，但却在学业考试中屡屡出现，将这现象映射至平时的教学，是否应该更进一步抓落实呢？

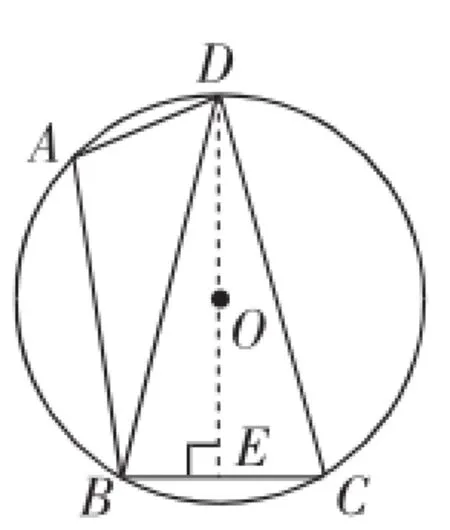
图2

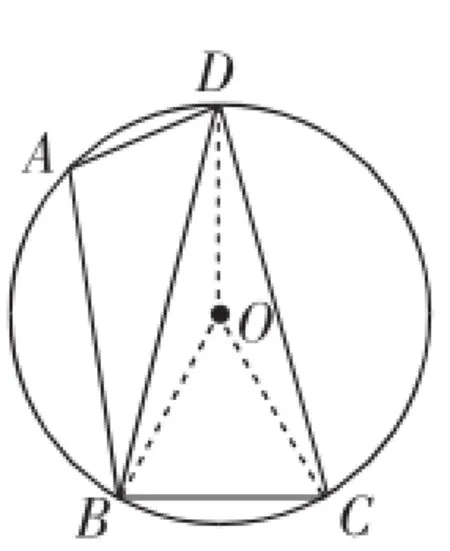
图3

四、多解思路及其分析

该题虽然为基础题，但第（1）小题的证明涉及的量较多，有圆心角、圆周角、弧、弦等，且能互相转化，因此解答思路也较多，故笔者重点对第（1）小题的证明进行多解思路的分析.

思路一：∠BAD=105°，根据圆内接四边形对角互补，得出∠C=75°，于是，∠C=∠DBC，则BD=CD.

思路二：将DA适当延长至点E，如图4，得到∠EAB=75°，利用外角等于內对角得到∠DCB=∠EAB=∠DBC=75°，则DB=DC.

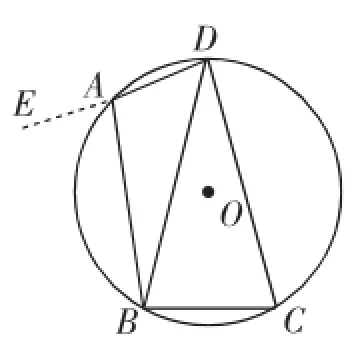
图4

【分析】思路一是命题者在命制试题时所想到的思路，也是学生解题时的“自然思路”，所得出的解法也就是最自然的解法，是最快速最直接能得出结论的方法，大多数学生都用到了该思路.思路二可谓是思路一的“孪生思路”，因为“圆内接四边形的外角等于内对角”和“圆内接四边形对角互补”原本就同气连枝.

思路三：连接AC，如图5，先利用圆周角定理得出∠DAC=∠DBC= 75°，进而得到∠BDC=∠BAC=30°，再用三角形内角和定理得出：∠DCB=∠DBC=75°，则DB=DC.

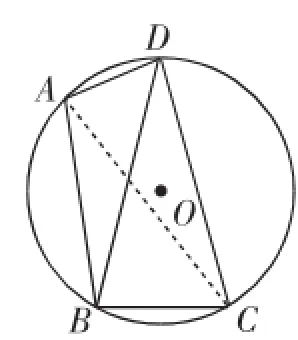
图5

思路四：连接OB、OC、OD，如图3，利用圆心角与圆周角的关系及周角和为360°，得到∠COD=∠BOD=150°，再利用OB=OC、OD=OD证明△DOB≅△DOC，则DB=DC.

思路五：连接OB、OC、OD，如图3，利用圆心角与圆周角的关系及周角和为360°，得到∠COD=∠BOD=150°（同思路4），再利用圆心角定理直接得出DB=DC.

【分析】思路三至思路五，虽都需添加辅助线，但至少整个推理过程完全正确，思路三运用圆周角定理配合三角形内角和定理，最终用“一个三角形中，等角对等边”得出，思路四与思路五的前半部分完全一样，只是思路四稍显复杂，需证一次三角形全等，思路五相对快捷一些，直接通过“相等的圆心角所对的弧相等”轻松得出结论.总而言之，这三种思路均通过圆周角、圆心角、弦之间的转化一步一步推理得出结论，先不论繁简程度，推理过程没有任何问题，也不失为一种好的解法，体现了“殊途同归”的解题思维本真.

思路六：利用圆周角与所对的弧之间的度数关系，得到弧BD的度数=1周角360°-弧BCD的度数=360°-2× 105°=150°，得到∠DCB=∠DBC=75°，则DB=DC.

思路七：利用圆周角与所对的弧的度数关系，根据弧BC+弧CD=弧BCD，由弧的关系转化到其所对圆周角的关系，得到∠BDC+∠DBC=∠BAC=105°，所以∠BDC= 30°，（或先得到B（C的度数等于60°，再得到∠BDC=30°）再利用三角形内角和为180°，得到∠DCB=∠DBC=75°，则DB=DC.

【分析】思路六和思路七的共同点是：均借助弧的关系得出其所对圆周角的关系，最终得到线段之间的关系.虽相比前几种解题思路，稍显不易想到，但仔细想来，圆的诸多性质追根溯源，不就是根据一周360°及圆的旋转不变性和轴对称性得来的吗？恰恰相反，能利用该思路解答的学生反而是对圆的本质掌握最好的学生.联想到平时的教学，教师是否能在课堂上多渗透如此体现圆本质的解题思路呢？可见，教学中如能让学生多掌握一种思路就能多增加一点思维宽度.

五、教学启示

通过上述分析和思考，得到了几点教学启示.

1.注重推理分析，关注思维发展性.

在教学中，做题、讲题的目的不仅仅在于让学生“懂”和“会”，还需要让学生的思维能力与品质得到不同程度的发展与提升.在分析问题时，如果能让学生就“如何做”“为什么这样做”“怎样想到这样做”等方面多做交流与思维展示及碰撞，同时，教师能给予合适的评价与引导，会有助于减少学生解题过程中的直观判断因素，增加其理性思考成分，并有助于提高学生的思维能力和品质.典型错误中的“直观看，缺推理”，正是由于平时教学中在问题分析方面的欠缺所造成的，如能在分析问题时对于“如何做”“为什么这样做”“怎样想到这样做”这一思维发展线加强重视，相信会减少这类错误的出现.

2.注重推理规范，加强思维缜密性.

在几何证明的教学过程中，要培养学生规范解题的习惯.论证问题时，首先要引导学生分析清已知条件与未知条件间的逻辑关系，有关系才能应用已知条件进行论证，没有关系则不能乱用条件证明，更不能为了证明结论而创造条件.如典型错误中的“造条件，缺推理”，正是因为学生没有弄清条件和结论之间的逻辑关系才造成的低级错误.借助图形直观解决问题是一种常用的解题方法，但“过度直观”也易造成解题过程的不严密.如典型错误中的两种“缺推理”，都应引起高度重视，特别是“合情推理”和“演绎推理”的正确运用需通过平时的教学让学生合理掌握，可借助“合情推理”来寻思路，用“演绎推理”来完成解答过程，加强思维缜密性的培养.

3.注重推理方法，培养思维多元性.

多种不同解题思路的探寻可以拓宽学生的思路，培养学生思维的发散性和融合性，使学生思维的角度更多，思维的范围更广，真正达到增加思维宽度，连线成面的效果.对于第（1）小题多种解法思路的探寻发现，该题的解题通法为利用圆中弧、圆心角、圆周角、弦之间的转化，进而证得结论成立.多样的解法呈现了“殊途同归”的多元化思路.可见，在平时的解题教学中，多种思路探究教学既能培养学生的多元化思维，还能帮助学生挖掘问题的本质，找到解题的通法，从而积累解题经验，建构解决问题的方法体系.

4.注重推理思想，助推思维灵活性.

数学思想方法是对数学知识、方法、规律的一种本质认识，是数学的精髓，是学生形成良好认知结构的纽带，是知识转化成能力的桥梁.当然，数学思想方法要在概念、性质、法则、公式、公理、定理的学习过程中适时渗透，让学生在掌握表层知识的同时，又能体悟到深层的数学思想方法，助推思维灵活性.该题作为一道基础题，所涉及的重要数学思想并不多，但转化思想、数形结合思想及建模思想还是有所体现的.转化思想用于各元素等量关系之间的转化，数形结合思想体现在通过角度的计算得出图形中重要元素的数量关系（相等或倍数），建模思想运用于采用何种模型，如三角形内角和模型、全等三角形模型、等腰三角形模型、圆内接四边形模型等.数学思想是数学思维的灵魂，平时的教学中，只有注重思想的渗透，才能给学生带来思维的可持续发展.

1.张克玉.2015年中考数学：阅卷报告——安徽第22题［J］.中学数学教学参考（中），2015（11）.

2.高峰.条件误用惹祸端转化无门陷艰难［J］.中学数学教学参考（中），2014（10）.

3.陈德前.重结果，轻过程，合情推理不合情［J］.中学数学教学参考（中），2014（10）.

4.姜晓翔，沈莹琪.挖掘本质出奇效双直模型巧解题——以一则教师说题案例说起［J］.中学数学（下），2014（11）.