归类究错：以分类讨论试题讲评为例——从两道“漏解”试题讲评说起

☉江苏建湖县高作中学薛金陵

归类究错：以分类讨论试题讲评为例
——从两道“漏解”试题讲评说起

☉江苏建湖县高作中学薛金陵

初三中考复习期间，学生会经历大量的模考训练，通过模考训练常常能查漏补缺，而考后的跟进讲评与订正，如果只是满足于就题讲题，出错一题修补一题，没有必要的归类究错，则往往订正效果并不明显.本文记录近期一次试卷讲评课上的关联式订正与究错，并给出相关解题教学的建议，供研讨.

一、“漏解”试题讲评实录

2图像交于点A（1，8）、B（-4，m）.

（1）略；

（2）略；

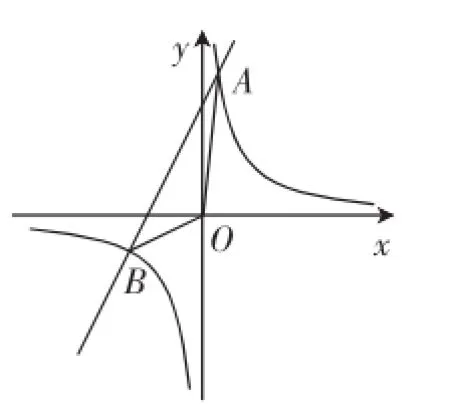
图1

（3）若M（x1，y1）、N（x2，y2）是反比例函数y=图像上的两点，且，指出点M、N各位于哪个象限，并简要说明理由.

批阅记录：第（3）问全班只有极少数学生“完整”解答，虽然多数学生都答出了“点M在第三象限，点N在第一象限”，但是解答过程中缺少必要的分类讨论.

讲评记录：由于第（3）问的条件只给了x1＜x2，并没有明确这两个自变量与0的大小关系，所以需要分三种情况：

①当x1＜x2＜0时，y1＞y2，不合题意，舍去；

②当x1＜0＜x2时，y1＜0，y2＞0，y1＜y2；

③当0＜x1＜x2时，y1＞y2，不合题意，舍去，

综上所述，点M在第三象限，点N在第一象限.

考题2：如图2，四边形ABCD为正方形.在边AD上取一点E，连接BE，使∠AEB=60°.

（1）利用尺规作图补全图形；（要求：保留作图痕迹，并简述作图步骤）

（2）取BE的中点M，过点M的直线交边AB、CD于点P、Q.

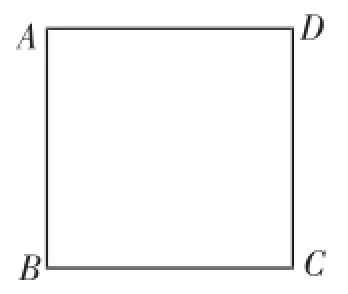
图2

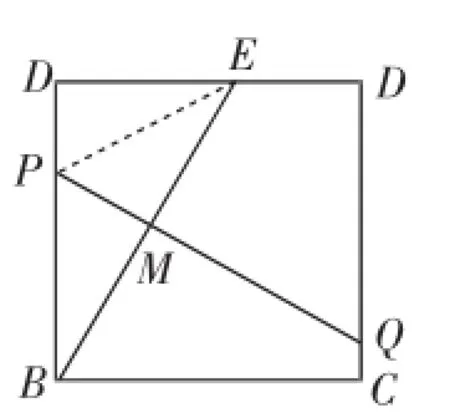
图3

①当PQ⊥BE时，求证：BP=2AP；

②当PQ=BE时，延长BE、CD交于N点，猜想NQ与MQ的数量关系，并说明理由.

批阅记录：第（1）问是尺规作图，不是本文阐释的重点，这里从略；

第（2）问整体正确率较高，但不少学生在证明时有思路回路，过程不简明；

第（3）问漏解严重，只有少数学生考虑了不同的位置情形，讲评时需要花时间在引导构图上.

讲评记录：第（2）问简明的证明思路如下：连接PE，如图3，容易得出PQ垂直平分BE.则PB=PE.于是∠PEB=∠PBE=90°-∠AEB=90°-60°=30°，所以∠APE=∠PBE+∠PEB=60°，则BP=EP=2AP.

对于第（3）问，有两种可能的数量关系：NQ=2MQ或NQ=MQ.理由如下：

如图4所示，过点Q作QF⊥AB于点F，交BE于点G，则QF=CB.在正方形ABCD中，AB=BC，则FQ=AB.接着可证出△ABE≌△FQP（HL）.所以∠FQP=∠ABE=30°.再结合∠MGQ=∠AEB=60°，有∠GMQ=90°.易得∠N=∠ABE= 30°.所以NQ=2MQ.

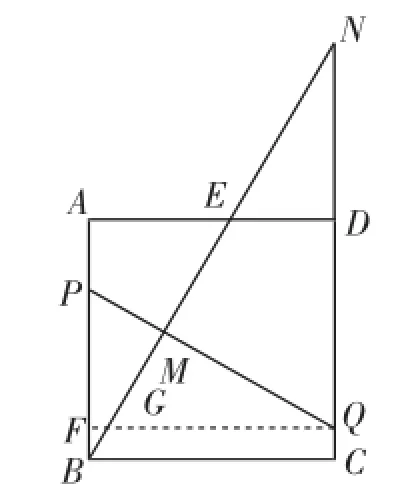
图4

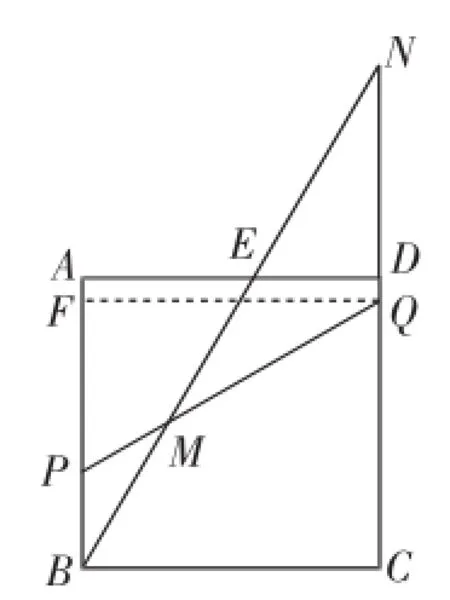
图5

如图5所示，过点Q作QF⊥AB于点F，交BE于点G，则QF=CB.同理可证△ABE≌△FQP.此时∠FPQ=∠AEB= 60°.∠EMQ=∠PMB=30°.所以∠N=∠EMQ，即NQ=MQ.

讲后引导学生回顾反思：上面两道考题出现在同一试卷中，全班有三分之二的学生两道题都漏解，有10人左右漏解一道，只有2人全部考虑全面，没有漏解.请这其中一个同学交流一下他的解答经验时，该同学指出由于条件x1＜x2，以及PQ=BE，都没有相应的图形，需要自已思考后构图，而构图需要考虑不同的可能.

教师点评：当图形的位置确定之后，通常大小关系（即数量关系）也随之确定；反之，如果图形之间存在某种数量关系，但并不一定能够唯一对应一种图形.简言之，位置关系确定后，可确定数量关系，但仅有数量关系，不一定有唯一对应的图形位置.这也是这类问题需要分类讨论的深层次原因.

二、关于分类讨论思想方法的教学思考

1.重视学科“研究套路”的渗透与强化，让纠错有“据”可依.

章建跃博士在多篇文献中反复指出数学学习的“研究套路”，比如，代数教学中，以“数”为例，常常先学习一类新数的概念及相关概念（如学生会明辨什么是实数，然后是与实数相关的概念，如相反数、倒数、绝对值、数轴等），接着是数的运算，数学运算又是先猜想、归纳或证明出数的运算法则，明确运算顺序，然后灵活运用运算律简化运算.再比如，几何教学中，在初中平面几何教学起始阶段，要引导学生知晓、理解并记牢几何图形的形状、大小和位置这三个方面.在后续教学中，要常常“回到”这样的基本套路中强化这些意识，无论是新引入一类平行四边形的研究，还是圆的学习，都可习惯性地问学生，如“现在我们开始学习平行四边形了，从平行四边形的边来看，它的位置、数量上有何关系？请大家探究”，或“同学们思考一下，你们觉得研究平行四边形的对角线，可以从哪些角度来研究”（预设：从对角线的位置关系、数量关系）.经常强化这样的套路意识，在学生解决需要分类讨论的问题出错后，就可通过追问引导他们明辨这些套路，使得他们自主纠错、发现错漏，促进自主究错的学力发展.

2.重视数学基本概念的教学，从“标准模式”到“非标准模式”.

分类讨论是每份试卷上必考的一种数学思想方法，表面上看主要考查学生严谨、细致的思维品质，深层次说，是考查学生对数学基本概念的深刻理解.追根究底，不少分类讨论问题出现漏解或重解，往往都是出错学生对数学概念的理解还不够深刻，比如，上文中的考题1，深层次究错的话，学生不只是由数量关系只想到一种位置关系出现漏解，而且也可归因到出错学生对反比例函数图像是双曲线，两支曲线分布在不同象限，理解不深，如果时时有反比例函数图像是双曲线，是两支的深刻印象，则解题时看到两个自变量，就不会想当然地把这两个自变量的值只考虑到一个象限中.所以，我们在教学基本概念时，需要重视学生对概念的深刻理解，比如《中学数学（下）》前一段时间有文章主张教学要重视从“标准模式”走向“非标准模式”就是一种积极的教学实践，值得我们学习和实践

3.重视订正讲评环节的链接，从深层次诊断错因追求标本兼治.

试卷讲评课是复习阶段十分重要的课型，当前的数学教学实际表明，日常教学中有大量的数学课堂在订正、讲评习题中度过，怎样把一些错题、易错题的讲评效果提升，是值得每一位教师认真思考和面对的现实课题.就本文写作意图来看，我们提供的两道错题从知识点上看不在同一个知识块下，但是从出错的深层次原因上看，则是因为对数量关系与位置关系之间的思辨、对应，所以将它们链接在一起教学、究错，有助于提高教学效果，强化学生以后遇到此类问题的分类讨论意识.

4.定理教学时需要引导学生“逆过来”思考，探究逆命题是否成立.

数学教学过程中有大量的定理教学，突出体现了几何教学中大量的定理，而这些定理往往都是由一道文字命题出发，经历画图，写出已知、求证，并证明的过程，很多定理教学都根据教材上的课时划分亦步亦趋，缺少必要的教材重组，比如，定理证明之后就是例题讲评、习题训练.我们可以在定理证明之后立即安排学生逆过来思考，探究条件、结论置换之后的逆命题是否为真命题，经常引导学生逆向思考，探究逆命题是否成立，对于学生深刻理解定理，理解题设与结论之间的互动、对应关系十分有益.近年来，我们在《中学数学（下）》见到大量著名特级教师李庾南老师的课例，我们看出李老师倡导的“学材再建构”的备课主张，就是旗帜鲜明的倡导源于教材、高于教材、重组教材的教学主张，值得我们一线教师深入实践和研习.

1.季卫东.变式取向：从“标准模式”到“非标准模式”——以“轴对称最值问题”解题教学为例［J］.中学数学（下），2014（3）.

2.鲍建生，顾冷沅等.变式教学研究［J］.数学教学，2003（1、2、3）.

3.许燕.从解题赏析走向教学研究——以2016年无锡卷第27题为例［J］.中学数学（下），2016（10）.

4.郑毓信.善于提问［J］.人民教育，2008（19）.

5.孟慧.几何综合题研究：从思路贯通到教学微设计［J］.中学数学（下），2016（9）.