复合材料基准值计算程序及其与可靠性关系
2017-04-20刘艳红王晓强
刘艳红,王晓强
(沈阳航空航天大学 a.计财处,b.航空航天工程学部(院),沈阳 110136)
复合材料基准值计算程序及其与可靠性关系
刘艳红a,王晓强b
(沈阳航空航天大学 a.计财处,b.航空航天工程学部(院),沈阳 110136)
通过MATLAB软件编写复合材料力学性能A、B基准值的计算程序,该计算程序采用Excel表格进行输入和输出,操作简单。通过数值验证可知:该计算程序结果正确,可以提高试验数据处理的效率。基于给定的安全系数,给出基准值与结构可靠性指标之间的关系表达式,明确了基准值与结构可靠性之间的内在关系。算例结果表明,基于B基准值的设计方法是可以满足结构可靠性设计要求的,但结构可靠性过高、偏于保守。
复合材料;基准值;计算程序;可靠性;安全系数
大量采用复合材料是飞机机身、机翼等结构减重的主要技术措施之一[1-3]。但是,复合材料结构的使用也引入了许多新的问题,其中之一就是复合材料的力学性能与金属材料相比,具有更大的分散性[4-5]。因此,在飞机复合材料结构设计中,如何确保飞机结构的安全性即如何经济合理地确定复合材料力学性能的基准值,是一个现实且非常重要的问题[6-7]。美国航空领域,基于统计分析方法,在MIL-HDBK-17-1F手册中给出了复合材料A、B基准值的计算方法。在此之后,美国FAA(Federal Aviation Administration)基于长期使用经验,对MIL-HDBK-17-1F手册中的计算方法进行了修订。在国外手册的研究成果基础之上,我国制定了航空行业标准HB 7618-2009。采用复合材料基准值的设计方法主要是考虑复合材料力学性能具有一定的分散性,经济合理地选取复合材料力学性能在实际设计中的取值问题。基于材料基准值的设计方法是利用实验数据,对材料力学性能进行统计分析确定其概率分布形式,然后在给定置信度下,将指定的下分位数做为基准值,即基准值是基于统计意义下的确定值。基于可靠性的设计方法也是利用统计方法确定各不确定量的概率分布形式[8-10],但与基准值设计方法不同的是“可靠性设计方法直接利用不确定量的概率分布进行结构设计,可以充分考虑复合材料力学性能的分散性”。综上,基准值设计方法是利用力学性能概率分布的下分位数进行结构设计,而可靠性是利用力学性能的概率分布进行复合材料结构设计[11-14],两种设计方法必然存在一定的内在关系。在目前的飞机结构设计过程中,复合材料力学性能的设计值一般采用B基准值[15-16]。同时,结构可靠性要求必须满足设计手册、规范中的相关要求。因此,需要明确采用基准值的设计方法与结构可靠性之间的内在关系,探讨复合材料基准值对应的结构可靠性对飞机结构设计是必要的。
本文首先对MIL-HDBK-17-1F手册中给出的基准值计算方法进行简要介绍;然后采用MATLAB软件编写复合材料基准值计算程序,并对自编程序进行验证;最后给出基准值与结构可靠性指标之间的关系表达式,进而明确了基准值设计方法与结构可靠性之间的内在关系。
1 基准值计算方法简介
在MIL-HDBK-17-1F复合材料设计手册中,给出了复合材料力学性能A、B基准值的定义。A基准值:基于统计的材料性能,在95%的置信度下99%的性能数值群不低于其值;B基准值:基于统计的材料性能,在95%的置信度下90%的性能数值群的值不低于其值。
用于计算基准值的方法取决于数据的特定,即数据是否为结构型数据。结构型数据是可以自然分组的数据,或其重要影响能随已知参数系统地变化的数据;非结构型数据是所有有关的信息全包含在响应测量值本身的数据。简而言之,组间差异可以忽略的数据、各批次数据可以合并的数据称为非结构数据,否则称为结构型数据。
对于非结构型数据,合并各批次数据,依次进行Weibull分布、正态分布和对数正态分布的拟合优度检验。若观测显著性水平(Observed Significance Level-OSL)大于0.05,则表明拟合成功;反之若OSL小于0.05,则表明拟合不成功。当以上3种分布的OSL没有一个大于0.05时,则需使用非参数基准值的计算方法。
对于结构型数据,根据确定性影响与随机性影响对数据进行分组,利用Levene检验判断数据来自几个批次。若数据来自同一批次,则按照非结构型数据计算基准值;若数据来自两批次,分别计算每个批次对应的基准值,然后取二者较小值;若数据来自3批次或多批次,采用ANOVA(Analysis of Variance)方法计算基准值。复合材料力学性能的A、B基准值的计算流程如图1所示。
2 基准值计算程序
2.1 主要计算公式
(1)K样本AD检验
K样本Anderson-Darling检验被用于检查数据组间的差异,以确定差异是明显或是可忽略,进而确定数据是结构型数据还是非结构型数据。
假设数据用xij表示,i=1,…,k和j=1,…,ni,其中i表示组号,j表示该组内观测值序号,则总观测值数量为n=n1+n2+…nk。将合并后的数据集合中的不同数值,按从小到大排序,记为z(1),z(2),…,z(L),其中L在存在相同值时小于n。
(1)
式(1)中:hj为合并样本中等于z(j)值的个数,Hj为合并样本中小于z(j)值的个数加上等于z(j)值的个数的一半,Fij为第i组中小于z(j)值的个数加上等于z(j)值的个数的一半。
ADK的临界值ADC(Critical Value of ADK)为

图1 基准值计算流程图
(2)
式中:σn为ADK的标准差。
如果临界值小于式(1)的检验统计量,则可断定各组是从不同母体中抽取的;否则接受各组来自同一母体的假设,即该数据可看成非结构型数据。
(2)Anderson-Darling检验

(3)
式(4)中:AD*为Anderson-Darling统计量的转换值,a,b和c为常数。
对于不同的分布,AD*具有不同的表达式、a,b和c也具有不同的值,详见MIL-HDBK-17-1F手册。
(3)Levene检验
Levene检验是用来确定k组的样本方差是否明显不同,该检验是非参数的,即它对关于潜在母体形式的假设要求不高。要进行该检验,首先要对数据进行转换,如下
(4)

然后对转换后的数据进行F检验,如果检验的统计量大于或等于F分布的分位数,那么可以断定方差明显不同。如果检验统计量小于F分布的分位数,那么接受方差相等的假设。如果检验拒绝了方差相等的检验,一般需要进行方差不等的原因调查。
复合材料基准值计算需要大量计算公式,这里只给出了几个主要公式,其它公式可参见MIL-HDBK-17-1F手册,这里不再赘述。
2.2 计算程序简介
本文根据MIL-HDBK-17-1F手册中给出的复合材料力学性能A、B基准值的计算方法,利用MATLAB软件编写相关计算程序。为便于工程使用,该程序输入和输出均采用Excel表格的形式,程序的输入和输出见图2。
2.3 计算程序验证
为验证自编程序的准确性,本文取MIL-HDBK-17-1F手册中的两个算例进行验证。算例1为非结构型数据,算例2为结构型数据,已知输入数据见表1。
对于算例1,由于ADK小于ADC,因此该数据属于非结构型数据。由于Weibull和正态分布对应的OSL均小于0.05,而对数正态分布的OSL大于0.05,因此认为利用对数正态分布对数据进行拟合是合适的。对于算例2,由于ADK大于ADC,因此该数据属于结构型数据。经计算F分布的统计量小于F分布的分位数,可以接受方差相等的假设。算例1和2的计算结果见表2和表3。由表2和表3可以看出:自编程序与MIL-HDBK-17-1F手册中给出的计算结果几乎是完全一样的,这说明自编程序是正确的。
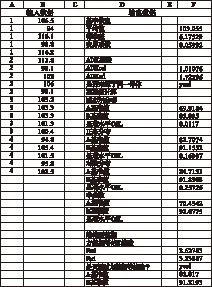
图2 输入与输出

算例1(非结构型数据)批次数据/MPa算例2(结构型数据)批次数据/MPa185.391328.1174197.121334.7674192.661347.7833196.431346.2661190.721338.7314195.842297.0387297.32293.45952109.472308.04192101.352326.4864298.012318.1297286.182309.04872100.913337.093396.053317.7319392.23321.4292390.863317.26523101.273291.88813101.234297.6943393.154327.39734114.324303.86294100.144313.0984491.244323.2769486.115312.9743493.425324.5192492.655334.5965597.585314.9458597.755322.7194597.956291.12155112.496309.7852595.756304.84995110.536288.01846294.1995

表2 计算结果(算例1)

表3 计算结果(算例2)
3 基准值与结构可靠性的关系
3.1 基本公式
在结构应力的基准值取值时,一般要保证99%的应力值低于该值[17],即概率分布的上分位数;在强度基准值取值时,一般要保证95%的强度值高于该值,即B基准值。当材料强度R与结构应力S均为正态随机变量时,强度与应力的基准值和其均值之间关系如下
(5)
式(5)中:Rk和Sk为强度和应力的基准值,μR和μS为强度和应力的均值,σR和σS为强度和应力的标准差,λR和λS为强度和应力的保证系数,VR和VS为强度和应力变异系数。
若应力S服从正态分布,此时λS=2.326 3;若强度R服从正态分布,对于B基准值λR=1.644 9,对于A基准值λR=2.326 3。当材料强度R与结构应力S不服从正态随机分布时,其基准值可采取统计方法进行计算。
基于结构可靠性理论,结构可靠度Pr的一般表达式为
(6)
式(6)中:fS,R(s,r)为强度和应力的联合概率密度函数。
当材料强度R与结构应力S相互独立时,有
(7)
式(7)中:fR(r)和fS(s)为强度和应力的概率密度函数。
当材料强度R与结构应力S均服从正态随机分布时,有
Pr=Φ(β)
(8)
式(8)中:Φ为标准正态分布的累积分布函数,β为可靠性指标。
(9)
可靠性安全系数γk的定义为
(10)

(11)
3.2 算例
以图2给出的数据作为复合材料的力学性能数据,即可靠性分析中的材料强度R。由图2中的计算结果可知:Weibull分布对应的OSL小于0.05,而正态分布的OSL大于0.05,因此认为材料强度R服从正态分布,其均值和变异系数分别为103.055 MPa和0.059 2。
在结构可靠性分析过程中,这里取结构应力S也服从正态分布,其均值μs通过给定一系列γk,然后通过式(10)进行求解,结构应力S的变异系数取为0.1,0.2和0.3。在γk的计算过程中,相关参数取值如下:λs=2.326 3,即99%的应力值低于应力基准值;λR= 1.644 9,即材料强度取B基准值。
当强度变异系数VR=0.059 2时的计算结果见表4,表4中0.9m表示小数点后有m个9,例如0.9425=0.999 925。由表4可以看出:(1)随着安全系数γk的增加,结构可靠度Pr在增加,即安全系数γk越大结构可靠性越高;(2)不同的变异系数Vs对应的结构可靠度是不同的,随着Vs的增加,结构可靠度减小,即结构应力的变异性越大,结构的可靠度越低;(3)对应不同的安全系数γk,结构可靠性均较高,最小的可靠度值(γk=1.25和Vs=0.3时)为0.94,对应的失效概率为1-0.999 9=1.0×10-4,即结构失效概率为万分之一。
表4中给出的数值结果是在VR=0.059 2下的计算结果,为了进一步讨论材料强度R的变异性VR对计算结果的影响,表5中给出了在Vs=0.3的情形下,不同VR对应的计算结果。由表5可知:随着安全系数γk的增加,结构可靠度Pr在增加;随着VR的增加,结构可靠度减小;对应不同的安全系数γk,结构可靠性均较高,最小值为0.94,即结构失效概率为万分之一。
在结构可靠性设计手册[18]上指出:对于军用飞机机体结构,其静强度可靠度通常要在0.94以上。由以上分析结果可以看出:(1)即便是安全系数取为1.25,基于复合材料B基准值的设计方法是可以满足结构可靠性设计要求的;(2)当安全系数取1.5和2.0时,结构可靠度分别在0.96和0.99以上,结构可靠度明显大于0.94,即明显大于设计手册中给出的可靠性要求。因此,采用复合材料B基准值的设计方法从可靠性的角度来看,还是较为保守的,这对飞机结构的轻量化设计是不利的,难以充分发挥复合材料的优势。
4 结论
本文通过MATLAB软件编写了复合材料力学性能A、B基准值的计算程序,该计算程序采用Excel表格进行输入和输出。输入文件按照格式要求进行输入即可,对工程技术人员没有其它要求;输出文件除了A、B基准值外,还包含各统计指标的具体值,便于工程应用。算例结果表明,该计算程序结果正确,能够大幅提高实验数据处理的计算效率。

表4 不同安全系数下的结构可靠度(VR=0.0592)

表5 不同安全系数下的结构可靠度(Vs=0.3)
探讨了当采用B基准值进行结构设计时,基准值与结构可靠性的内在关系。算例分析结果表明:
(1)随着安全系数的增加,结构可靠度增加,即便是安全系数取为1.25,基于复合材料B基准值的设计方法是可以满足结构可靠性设计要求的;
(2)当安全系数取1.5和2.0时,结构可靠度分别在0.96和0.99以上,结构可靠度明显大于设计手册中给出的可靠性要求。因此,采用复合材料B基准值的设计方法从可靠性的角度来看,还是较为保守的。
[1]杨乃宾,章怡宁.复合材料飞机结构设计[M].北京:航空工业出版社,2004.
[2]赵维涛,刘炜华,杨其蛟.复合材料加筋板极限承载能力分析[J].沈阳航空航天大学学报,2015,32(4):37-43.
[3]赵维涛,杨其蛟,刘炜华.复合材料加筋板低速冲击响应分析[J].沈阳航空航天大学学报,2015,32(3):1-5.
[4]王佩艳,岳珠峰.大子样下复合材料层合板拉伸性能分散性研究[J].机械强度,2007,29(6):1005-1008.
[5]朱振涛,王佩艳,王富生,等.复合材料层合板拉压和面内剪切性能的分散性实验研究[J].材料工程,2010(6):20-25.
[6]杨乃奎,梁伟.大飞机复合材料结构设计导论[M].北京:航空工业出版社,2009.
[7]牛春匀.实用飞机复合材料结构设计与制造[M].北京:航空工业出版社,2010.
[8]ZHIPING QIU,REN HUANG,XIAOJUN WANG,et al.Structural reliability analysis and reliability-based design optimization:Recent advances[J].Science China Physics,Mechanics and Astronomy,2013,56(9):1611-1618.
[10]ALI HAERI,MOHAMMAD JAVAD FADAEE.Efficient reliability analysis of laminated composites using advanced Kriging surrogate model[J].Composite Structures,2016,149:26-32.
[11]王向阳,陈建桥.复合材料层合板的可靠性优化和鲁棒特征[J].华中科技大学学报,2006,34(8):94-96.
[12]安伟光,赵维涛,杨多和.复合材料层合板的可靠性分析方法[J].宇航学报,2005,26(5):672-675.
[13]陈建桥,许玉荣,魏俊红.复合材料层合板的极限强度分析与可靠性优化设计[J].机械强度,2007,29(2):241-246.
[14]孙海龙,郭书祥,韩一磊.基于响应面法的复合材料层合板平面应力强度可靠性分析[J].军械工程学院学报,2008,20(1):19-23.
[15]CHONG WANG,ZHIPING QIU,XIAOJUN WANG,et al.Interval finite element analysis and reliability-based optimization of coupled structural-acoustic system with uncertain parameters[J].Finite Elements in Analysis and Design,2014,91(8):108-114.
[16]王冲,邱志平,吴迪,等.含区间参数的结构-声耦合系统可靠性优化设计[J].振动工程学报,2014,27(5):728-733.
[17]王善,何健.导弹结构可靠性[M].哈尔滨:哈尔滨工程大学出版社,2002.
[18]刘文珽.结构可靠性设计手册[M].北京:国防工业出版社,2008.
(责任编辑:吴萍 英文审校:赵欢)
Calculation programming of basis value for composite material and its relationship with reliability
LIU Yan-honga,WANG Xiao-qiangb
(a.Finance Department,b.Faculty of Aerospace Engineering,Shenyang Aerospace University,Shenyang 110136,China)
A calculation programming of A and B basis values for mechanical properties of composite materials was compiled by MATLAB software.Input and output of the program was achieved by Excel,thus operation of the calculation programming was simple.Numerical examples show that the results of the calculation programming are correct.The program can improve the processing efficiency of experimental data.The relationship between the basis value and structural reliability index was obtained and clarified based on the given safety factor.The results show that the design method based on B basis value can meet the requirements of structural reliability design,but its structure reliability is too high and trend to be conservative.
composite materials;basis value;calculation programming;reliability;safety factor
2016-11-18
国家自然科学基金(项目编号:11602150);辽宁省自然科学基金(项目编号:201602579)
刘艳红(1978-),女,辽宁沈阳人,会计师,主要研究方向:可靠性工程与统计学,E-mail:sau_lyh@163.com。
2095-1248(2017)01-0037-07
V215.7
A
10.3969/j.issn.2095-1248.2017.01.006
