石墨炔纳米带热传导的分子动力学模拟
2017-04-20,,
,,
(福州大学 电气工程与自动化学院,福建 福州 350108)
1 引言
电子器件随着制造工艺的不断发展,微型化达到纳米量级,但是急剧减小的尺寸引起器件内热量快速增加,于是纳米尺度下的器件能否稳定运行取决于其产生的热量转移效率的高低。只有热量得到及时的排出,器件内部的局部温度才不会超过其正常工作温度,有利于延长器件的使用寿命,否则散热问题将严重制约器件微型化的进一步发展。
Baughman等[1]预测了一种新型的碳结构-石墨炔。Li等[2]利用六炔基苯在铜片催化的作用下发生偶联反应,在铜片表面上成功制备出大块 graphdiyne 薄膜,引起科学界对 graphyne 的关注热潮。Zhang等[3]通过分子动力学模拟方法研究了graphyne的导热系数,结果表明graphyne存在乙炔链使得其导热系数低于石墨烯的。欧阳等[4]通过格林方法对graphyne纳米带的热输运进行研究,结果发现graphyne纳米带的热导率与其手性有关。对于小尺寸的石墨炔纳米带的尺寸效应及Airebo势函数与Tersoff势函数对热导率的影响文献比较少看到。
因为纳米尺度下的石墨炔结构的变化会造成声子在传输过程中的声子移动速度和平均自由程发生变化,将影响声子的传热效率[5]。为了更好地预计和控制石墨炔纳米带热导率,本文主要研究的是长度和宽度及势函数对石墨炔纳米带热导率的影响。
2 分子动力学模拟
2.1 研究方法
分子动力学模拟方法是利用计算机进行模拟实验,来研究和反应整个过程,这对于理论计算和实验都具有重要意义。该法不仅可以“监控”原子,获得原子整个过程的运动轨迹,也可以像作实验一样,对有兴趣的量进行一系列的观察。该法多用于多粒子体系中,其核心思想是将体系中的粒子当作经典粒子,使得粒子的运动过程遵循经典牛顿运动定律。本文通过分子动力学方法,利用经典牛顿力学可得到体系中所有粒子的运动轨迹,从而得到该体系随时间变化的规律,再通过统计力学理论计算出体系的一些参数及热输运性质,然后通过这些数据计算得到温度梯度,再带入热导率公式求出导热系数,如图1所示。
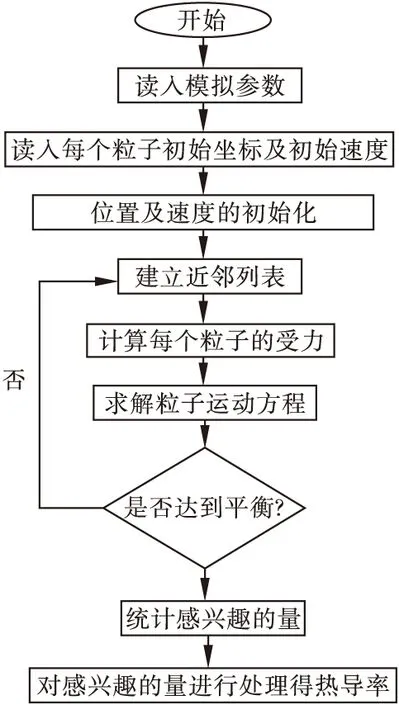
图1 分子动力学基本流程图
2.2 模型构建
石墨炔是由 1,3-二炔键将苯环共轭连接形成的二维平面网络结构,它具有丰富的碳化学键,大的共轭体系、宽面间距、优良的化学稳定性以及半导体性能如图2所示。利用MS软件构建石墨炔纳米带模型,根据不同的切割方向可以切得扶手椅型(armchair)和锯齿型(zigzag)石墨炔纳米带,如图3所示。
2.3 势函数的选取
在分子动力学模拟中,原子与原子之间的相互作用力由势函数来体现。对于分子动力学模拟来说,势能函数的选取决定着模拟计算的准度和精度。对于以碳为成分的物质和材料诸如石墨、金刚石、碳纳米管、石墨炔、石墨烯等,采用的势函数大多是Airebo势函数[6]。Airebo势函数是在Rebo势函数的基础上改进和推广的,通过在Rebo势函数中加入原子与原子之间的长程作用能和原子与原子之间及分子与原子之间的扭曲作用能,同时Airebo势是一个依赖于周围原子与原子之间的成键强度及键与键之间的耦合作用强度。Airebo势函数的优势在于它具有更高的精度,能精确的描述碳碳、碳氢之间的相互作用。因此,在本篇论文中,研究石墨炔纳米带的热导率,C-C原子之间的相互作用采用Airebo势函数来描述。

图2 石墨炔原胞

图3 石墨炔纳米带结构
在Rebo势函数的基础上,增加并加以改进了长程相互作用项和扭曲项,得到了我们所需要的Airebo势函数,它是一个依赖于周围原子配置的键合强度的势函数。其表达式为:
(1)

(2)
(3)
其中
VR(r)=fc(r)(1+Q/rAe-αr)
(4)
(5)
2.4 非平衡分子动力学方法
目前常见的关于用分子动力学方法模拟材料的导热性能有以下几种方法,分别是Green-Kubo 平衡态分子动力学方法(EMD)[7-8]、正向非平衡态分子动力学方法(Non-Equilibrium Molecular Dynamics,NEMD)[9]和Muller-Plathe 逆向非平衡态分子动力学方法(RNEMD)[10]。由于EMD 方法难以处理单质以外的物质,所以通常在微正则或正则系综下进行模拟。
本文采用的方法是非平衡分子动力学模拟方法(NEMD),该法是由 Muller-Plathe[11]提出的,是通过交换粒子的速度实现外加热流的算法,该算法所描述的是每隔N个时间步长交换任何两个不同区域内的两粒子间的速度,从而产生温度梯度,利用公式得到热导率。位于纳米带中间的是热层,位于带两端的是冷层,且在轴向设置周期边界条件,如图4所示。通过交换热层运动最慢的原子的速度和冷层运动最快的原子,实现热层和冷层间的能量交换,结果是热层更热、冷层更冷,从而实现热层到冷层方向的热传导。产生的热传导方向与粒子速度交换引起的能量传递方向相反[12]。
某一时刻第k层的温度Tk为:
(6)
其中,N为层中的原子数,mi表示i原子的质量,vi为对应原子的速度,kB=1.3806505×10-23J×K-1为Boltzmann常量。
通过得到的动能差就能求得体系所施加的热流值,进一步求得石墨炔纳米带体系的导热系数为:
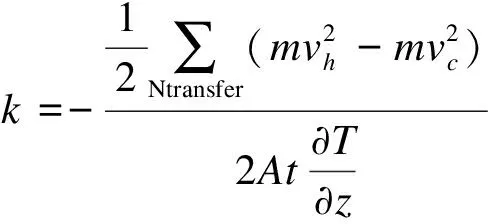
(7)

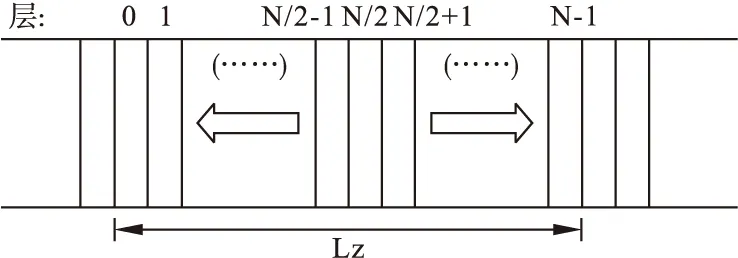
图4 交换速度方法示意图
3 模拟结果分析
在非平衡态分子动力学模拟过程中,判断模拟结果可靠性的一个重要原则就是沿着热流方向建立的温度梯度应该呈线性分布。整个模拟结构的温度曲线除了在热域和冷域附近区域出现较大波动外,在模拟结构的中间区域均表现出了一致的线性度。热域和冷域附近区域出现较大波动在非平衡态分子动力学模拟中总是存在的,这是由于声子在热域和冷域发生了强烈的散射,导致温度曲线出现了非线性。通过模拟结构的温度曲线获取温度梯度时,本文只考虑了模拟结构中间的线性区域,所以使用Fourier定律计算热导率是可行的[14]。
为了加快计算速率和通过计算精度,使用Verlet算法求解运动方程,积分时间步长为0.4fs。整个模拟过程分为3步:首先,在等温等压正则(NPT)系综(模拟过程中保持N-原子数量,P-压力,T-温度不变的系综)下模拟4×105step;再转到正则(NVT)系综(模拟过程中保持N-原子数量、V-体积、T-温度不变的系综)下继续运行4×105step;然后在微正则(NVE)系综下运行2×105step,通过交换冷热原子使系统内部形成一定的温差,并统计系统产生的热流和响应的温差,最后通过热流与温度梯度的比值求得纳米带的热导率。
3.1 轴向长度、宽度对AGYNRs热导率的影响
本文首先在室温(300K)下模拟相同宽度的AGYNRs热导率与其长度间的关系,分别计算了宽固定为2.4699,3.7409,4.9398nm,长10.5,21,30.4,42,63和84nm的扶手椅型石墨炔纳米带的热导率,计算结果如图5所示。由图5可以得到:同一宽度下,石墨炔纳米带热导率随着AGYNRs长度的增加而增加,并且直接到84nm时,热导率为26.7701W/m·K,未收敛,说明石墨炔的分子平均自由程(polyatomic molecule mean free path)远大于84nm。本文模拟的最大尺寸长为84nm,可见热导率的大小与尺寸有关[15],由于分子动力学模拟的尺寸是有限的,当模拟的尺寸小于其分子的平均自由程时会出现Casimir限制效应[7],使得模拟得到的热导率要比实验值小,随着长度的继续增加,热导率会趋于一个稳定值。不同长度下的AGYNRs,长度大的横截面积大。在AGYNRs中,声子的散射主要受边界的限制,根据声子气动模型和弹射声子模型,相同条件下热量的输运主要依靠原子的振动,横截面积越大,其对声子面内传输的影响越小,故横截面积大的热导率较大。由图5还可以看出,宽度为2.4699,3.7409,4.9398nm 三个尺寸下,宽度对热导率的影响不大。
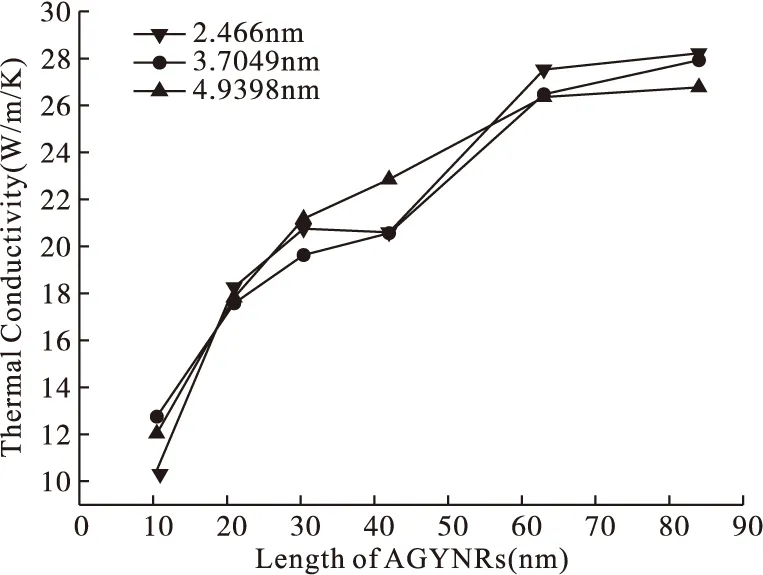
图5 完整石墨炔热导率和乙炔链上单空位缺陷对比
3.2 势函数对ZGYNRs热导率的影响
图6是锯齿型石墨炔纳米带在不同势函数时计算得到的热导率,其中锯齿型纳米带的宽度为63nm。从图中可以看出,该尺寸下,采用Airebo势函数计算得到的热导率高于采用Tersoff势函数计算得到的热导率。
4 结语
本文使用非平衡态分子动力学方法计算了AGYNRs的热导率。在室温下,对于相同宽度的同种类型石墨炔纳米带,热导率随着纳米带长度的增加而逐渐增大。采用Airebo势函数计算得到的热导率高于采用Tersoff计算得到的热导率。

图6 利用Airebo势函数与Tersoff势函数得到石墨炔纳米带热导率对比
[1]Baughman R H,Eckhardt H,Kertesz M.Structure-property predictions for new planar forms of carbon:Layered phases containing sp2 and sp atoms[J].The Journal of chemical physics,1987,87(11):6687-6699.
[2]Li J,Porter L,Yip S 1998 J.Nucl.Mater.255 139
[3]Zhang Y Y,Pei Q X,Wang C M.A molecular dynamics investigation on thermal conductivity of graphynes[J].Computational Materials Science,2012,65:406-410.
[4]Ouyang T,Chen Y,Liu L M,et al.Thermal transport in graphyne nanoribbons[J].Physical Review B,2012,85(23):235436.
[5]温志宏.石墨炔纳米管热导率的分子动力学模拟[D].湘潭大学,2014.
[6]Stuart S J,Tutein A B,Harrison J A.The J Chem Phys,2000,112(14):6472-6486.
[7]Schelling P K,Phillpot S R,Keblinski P.Phys Rev B,2002,65(14):144306.
[9]Berber S,Kwon Y K,Tománek D 2000 Phys Rev Lett.84,4613
[10]Muller-Plathe 1999 Phys.Rev.E 59 4894.
[11]Florian Muller-Plathe 1997 J.Chem.Phys.106 6082.
[12]赵晗,周丽娜,魏东山,等.石墨炔纳米管热导率的分子动力学模拟研究[C]//中国化学会第 29 届学术年会摘要集——第27 分会:多孔功能材料,2014.
[13]杨平,王晓亮,李培,等.氮掺杂和空位对石墨烯纳米带热导率影响的分子动力学模拟[J].物理学报,2012,61(7):76501-076501.
[14]魏志勇,毕可东,陈云飞.石墨烯纳米带热导率的分子动力学模拟[J].东南大学学报(自然科学版),2010,40(2):306-310.
[15]姚承军,汪晓明,李莹莹,等.一维到二维石墨烯声子热传导的分子动力学模拟[J].扬州大学学报(自然科学版),2013(1):22-26.
