浅谈“数形结合”思想在小学数学中的意义

朱政美

小学数学中有两大研究对象：“数”与“形”，这二者的矛盾统一是小学数学发展的内在因素，贯穿于数学发展中的一条主线就是数形结合，数形结合使数学在教学实践中的应用更加宽泛：（1）凭借图形的性质可以将诸多比较抽象的数学概念和数量关系形象化、简单化，给学生一种较直观的感受；（2）将教材中的一些图形问题转化为代数问题，可以使学生收获较准确的结论。这二者的概念相互转换，相互渗透，不仅可以使解题思维更加轻便，还能拓展学生的解题思路，为学生探索小学数学问题开辟了一条重要的途径。

一直以来，在小学数学教学过程中，一条明线是数学知识，得到广大数学老师的高度重视；一条暗线是数学思想方法，这一条线索容易被教师忽视。身为一线教师，如何在数学教学时系统地运用数形结合思想？“数形结合”思想在小学数学中有什么重要意义呢？

一、小学数学教学中数形结合是常用的数学思维方法

数形结合思想的实质就是通过数与形之间的相互转化，把相对抽象的一些数量关系，通过一些方法，转化为适当的几何图形，从所转换的图形结构相对直观地发现一些数量之间存在的联系，可以解决数量关系的数学问题。

现今的小学数学教学中，广大教师用得最多的是前者，而在数学应用题的分析求解中，一般是把数量关系转化成直观的线段图。但是，这也不是唯一的解决方式。在不同的数学问题中，也可把数量关系转化为不同的图形。只是这当中有一个原则：能把数与量的关系转换为最清晰、最直接的图形，这才是解决问题最佳的选择。

例1.平均分一盒糖果给三个小朋友，如果每人吃掉4块，那么三人剩下的糖块数之和恰好是原糖果数的1/3，原糖果有多少块？

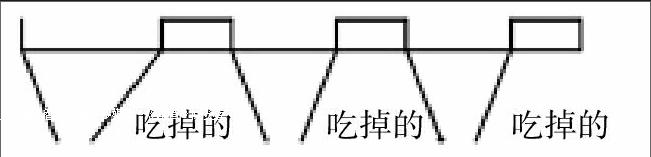
分析与解答：如用线段图表示数量关系，则如下图所示，其中小方框表示每人剩下的糖块数：

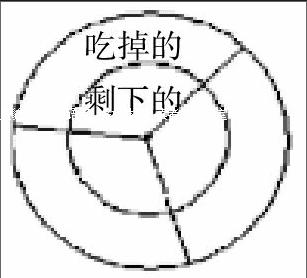
由于题目给出的是三人剩下的糖块数之和，与原糖果数的关系，在以上线段图中，三人剩下的糖块数是三条未带斜线且各自分离的线段，较难发现三条带斜线的线段长的和与整条线段长之间的数量关系，因此，这不是最佳的选择图形。我们希望选择的图形能够一目了然地看出“三人剩下的糖块数之和恰好是糖果数的1/3”，就是说，能把“三人剩下的糖块数之和”在图形中连成一片，并且能直截了当地看出它与原糖果数之间的关系。为此，我们画一个大圆，并且大圆的面积表示原糖块数。把大圆三等分，每份即表示每位小朋友分得的糖块数。在大圆中再画一个小同心圆（小圆半径约等于大圆半径的0.6），用小同心圆的面积表示三人剩下的糖块数之和，于是圆环的面积则表示三人吃掉的糖块数之和。如下图所示：这样一来，数量关系就完全明朗清晰了。

答：原有糖果18块。

从以上解题过程可以看出，线段图仍是揭示小学数学应用题中数量关系基本的、自然的手段。对于某些题，如线段图不能清晰地显示其数量关系，则可以通过对线段图的分析与改造，设计构造出能清晰地显示其数量关系的其他图形，使解题过程变得更简洁、更方便。

二、数形结合的思维可以激发学生的求知欲，调动学生学习的积极性

数形结合思想，通过教师创设一些與知识相关的情境，调动学生的学习动力，进而产生强烈的学习积极性。例如，在教学“比例尺”时，老师可以先出示一张我们扬州市的地图，富有感情地介绍：扬州地灵人杰，它南濒长江，西连南京，北负淮河，中贯京杭大运河，是一座工商繁荣、文教发达和风景优美的旅游城市。总面积6638平方公里。接着老师可以提问：“这么广大的疆域怎么能画在一张纸上呢？”如此一问，学生的好奇心和求知欲被激发，教学过程就这样在相对轻松愉快的气氛中向前推进。

还可以通过学生与学生之间的相互合作、相互观察、相互探索、相互合作、相互交流，让不同知识水平的学生在小组学习过程中进行互相补充、互相学习。

三、数形结合可以提高学生的思维能力，帮助学生解决疑难问题

在数学教学过程中，如何巧妙运用数形结合的思维解题，实际上就是一个“数”与“形”互相转化、相互演变的过程，也就是把题目中的数量关系转化成相对直观的图形，将比较抽象的数量关系形象化，再根据对图形的一系列观察与分析，逐步转化成数学算式，使之解决问题。由于相对抽象的思维背后有相对形象的思维作为支持，才能使解决问题的办法变得十分巧妙。

参考文献：

[1]孙嘉洁.小学算术的结构化教学设计[D].福建师范大学，2015.

[2]聂和冰.小学数学中渗透抽象思想的研究[D].华中师范大学，2015.

编辑 温雪莲