层状横观各向同性地基性质对刚性条基摇摆振动的影响

艾智勇， 任广鹏

(1. 同济大学 地下建筑与工程系，上海 200092； 2. 同济大学 岩土及地下工程教育部重点实验室， 上海 200092)

层状横观各向同性地基性质对刚性条基摇摆振动的影响

艾智勇1，2， 任广鹏1，2

(1. 同济大学 地下建筑与工程系，上海 200092； 2. 同济大学 岩土及地下工程教育部重点实验室， 上海 200092)

分析了土体的横观各向同性及层状性质对刚性条形基础摇摆振动的影响。首先利用解析层元法得出层状横观各向同性地基的总刚度矩阵。再根据刚性条形基础与地基相互作用的混合边值条件，建立了一组对偶积分方程，并借助Jacobi正交多项式求解了该对偶积分方程，从而得到地基动力柔度系数。计算结果与已有文献的结果吻合较好。同时，算例结果表明：土的水平向与竖向弹性模量比的减小、竖向的剪切模量与弹性模量比的增大,以及水平向泊松比与竖向泊松比比值的增大,都将导致地基动力柔度系数增大；而且,层状地基中上层土的弹性模量的减小使得地基动力柔度系数也增大。

摇摆振动； 层状地基； 横观各向同性； 对偶积分方程

研究地基土和基础在动力荷载作用下的响应，对地震工程及动力机器基础等实际问题具有一定的指导意义。LAMB[1]首先研究了均匀弹性半空间体在表面振动荷载作用下的响应；马晓华等[2]研究了饱和均质地基上条形弹性基础的摇摆振动问题；胡灿阳等[3]采用锥体模型分析了均质半空间内埋置圆盘平动和转动时的地基阻抗。考虑到天然土体是由长期自然沉积而形成，且往往呈现出横观各向同性的性质。STONELEY[4]研究了横观各向同性弹性半空间体内波的传播问题；KHOJASTEH等[5-6]利用位移势原理推导出了两层及多层横观各向同性弹性半空间体的三维动力格林函数；AI等[7-8]求出了层状横观各向同性弹性半空间在竖向和水平简谐荷载作用下的解析层元解。何芳社等[9]等采用Fourier-Bessel级数分析了横观各向同性饱和半空间上圆形环板的简谐振动。

解析层元法的优势在于数值计算过程中只涉及负指数函数、土体材料参数和土层厚度，这使得计算过程更加稳定有效。故本文运用解析层元法研究横观各向同性地基上刚性条形基础的摇摆振动问题，并通过算例分析了横观各向同性参数和成层特性对基础摇摆振动的影响。

1 平面横观各向同性层状地基解析层元

AI等利用积分变换等方法推导出了单层和多层平面横观各向同性地基动力问题的解析层元解，其中变换域中单层地基的解析层元如式(1)，

(1)

变换域中下卧半空间的解析层元如式(2)，

(2)

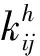
(3a)

(3b)

对于多层半空间，将式(1)应用于层状地基的每一层，将式(2)应用于下卧半空间，并结合层间连续性条件和式(3)，则可建立层状土体的总刚度矩阵：

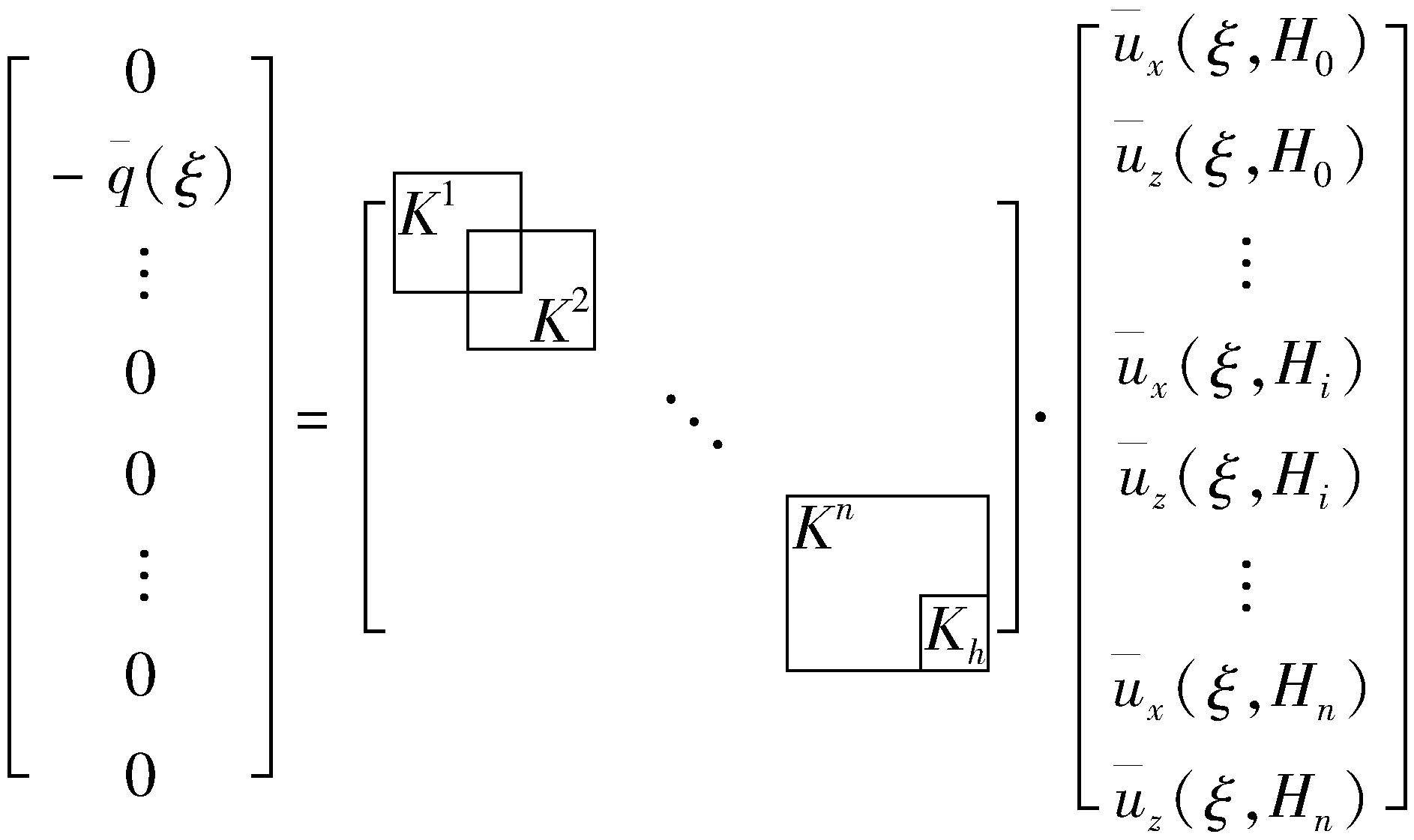
(4)

式中:Ki为第i层地基的解析层元;Kh为下卧半空间的解析层元。

2 层状地基与刚性条形基础共同作用

刚性条形基础在横观各向同性层状地基表面作摇摆振动，如图1所示。

假定刚性条形基础与地基完全光滑接触，且地基表面土体的剪应力为零。若在条形基础底部给定位移，则边界条件为

(5a)

式中:q(x)为接触应力;基础宽度为2b;转角为θ。

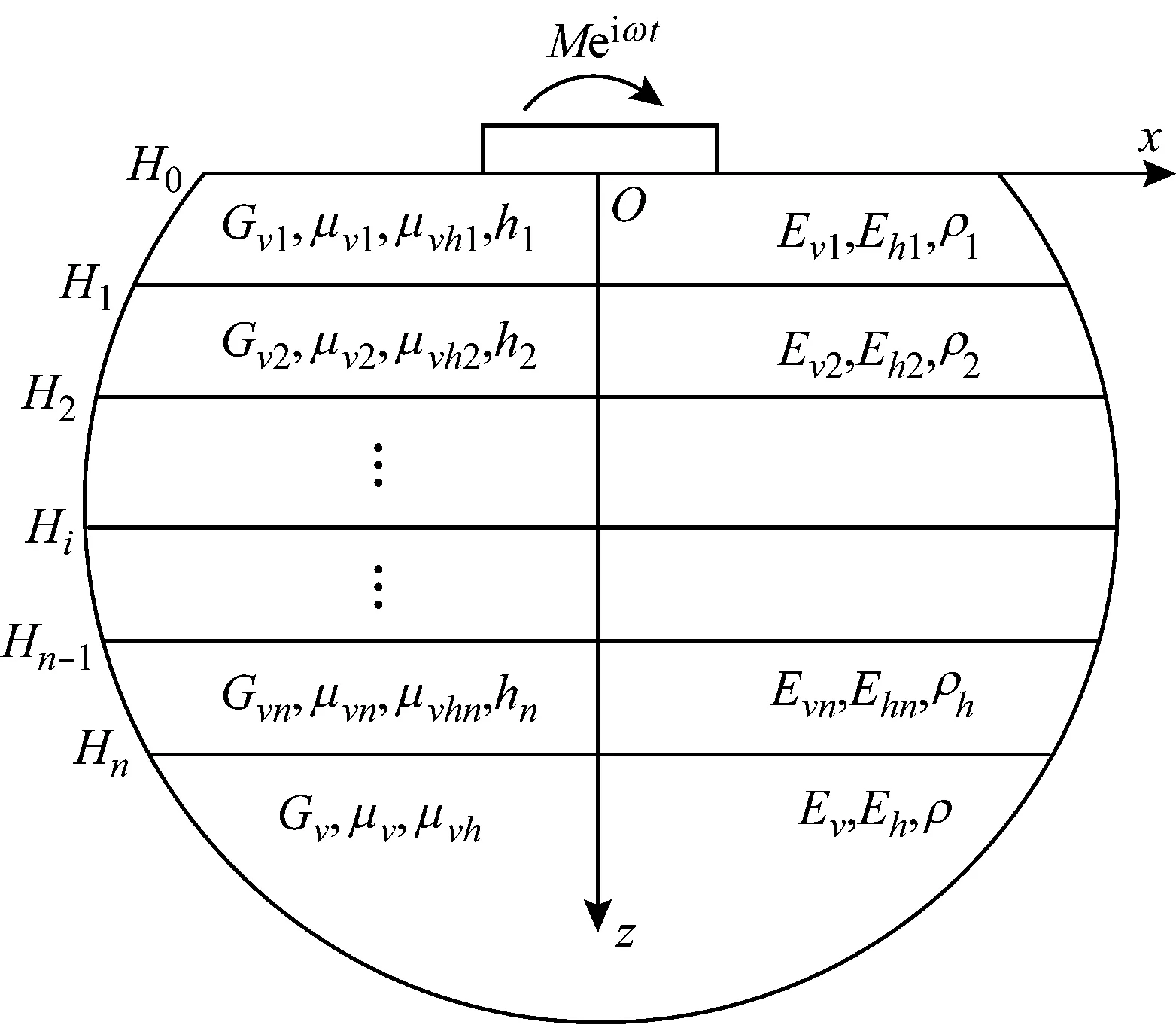
图1 刚性条形基础与层状横观各向同性地基相互作用

式(5)进行Fourier变换后代入式(4)，可得：

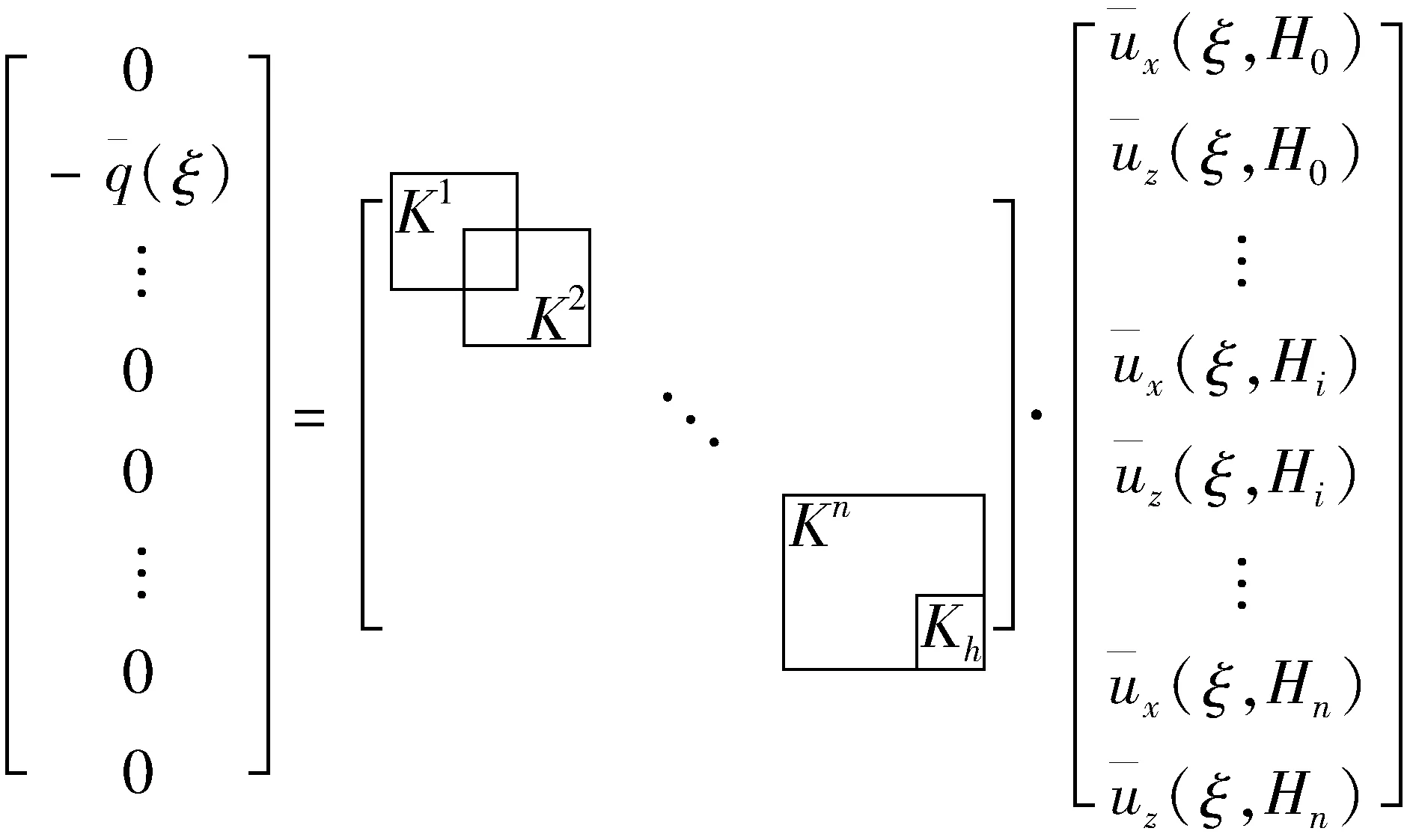
(6)

展开式(6)，可得：

(7)

式中，k*22为刚度矩阵求逆之后第2行第2列的元素。

结合式(5b)、式(5d)和式(7)可得一组对偶方程如下：

(8a)

(8b)

3 对偶积分方程求解

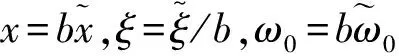
(9a)

(9b)

(10)

式中，an为待定系数， 并有如下关系式：

(11)

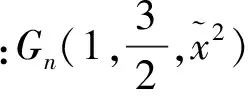
结合式(11)，并对式(10)进行Fourier变换得：

(12)

考虑到如下关系式：

(13)

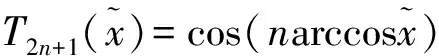
将式(12)代入式(9a)，则得：

(14)

再利用下列关系式：

(15)

将式(15)代入式(14)得：

(16)

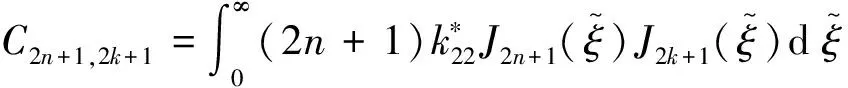
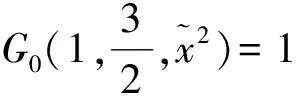
(17)

由式(17)求出a0,a1,…,an后，则基底反力的合力为

(18)

根据文献[11]，定义基底反力的合力：

(19)

则地基的动力柔度系数为

(20)

需要说明的是，为了避免在数值逆变换中出现奇异性，本文人为设置地基的阻尼比为0.01。文献[7]已证明这种人为增加的小阻尼对计算结果的影响可以忽略，因此本文的理论仍适用于纯弹性体。鉴于本文的数值计算在复数域内进行，计算所求的a0为复数值，因此地基的动力柔度系数CV由实部Re[CV]和虚部lm[CV]组成。

4 数值验证

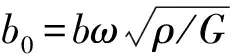
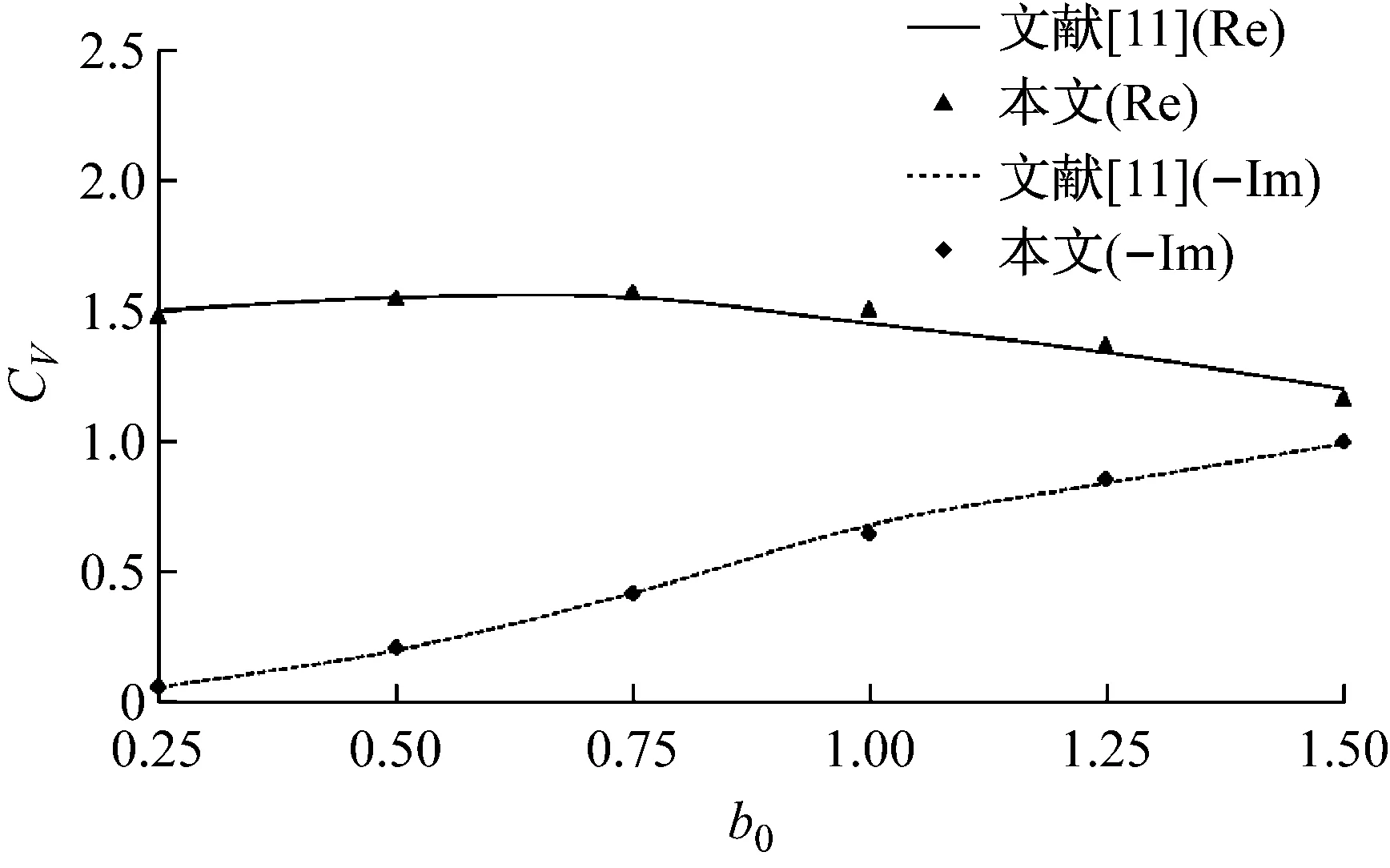
图2 与文献[11]的地基动力柔度系数结果对比

5 横观各向同性参数影响

5.1 横观各向同性参数n对柔度系数的影响

肖仁成等[12]对9种来自不同国家的横观各向同性土层试验数据进行了总结，故本文横观各向同性参数的取值参考了他们的工作。由于大多数地基Eh>Ev，在m=0.4，l=1情况下，分别选取n=1,2,3的情况进行计算，其它条件与验证算例相同。计算出的地基动力柔度系数如图3所示，由图3可以看出：在其它条件相同的情况下，地基动力柔度系数实部和虚部的绝对值，随着水平向与竖向弹性模量比n的增大而减小。

5.2 横观各向同性参数m对柔度系数的影响

在n=1，l=1情况下，分别取m=0.2,0.3,0.4，其它条件与验证算例相同，分析竖向的剪切模量与弹性模量比m对地基动力柔度系数的影响，计算结果如图4所示。由图4可以看出：地基动力柔度系数实部和虚部的绝对值随着竖向的剪切模量与弹性模量比m的增大而增大，并且动力柔度系数随无量纲频率变化的趋势与图3相似。

图3 n对地基动力柔度系数的影响

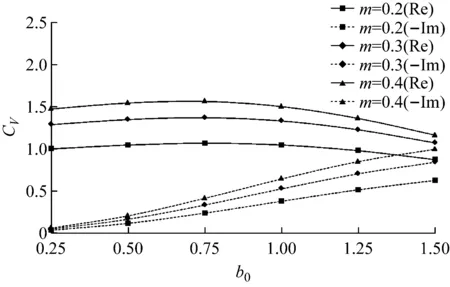
图4 m对地基动力柔度系数的影响

5.3 横观各向同性参数l对柔度系数的影响

在m=0.4，n=1情况下，分别取l=1,1.5,2，分析水平向泊松比与竖向泊松比的比值l对地基动力柔度系数的影响，计算结果如图5所示。由图5可以看出：地基动力柔度系数实部和虚部的绝对值随着水平向泊松比与竖向泊松比的比值l的增大而增大。

图5 l对地基动力柔度系数的影响

综上可见，横观各向同性参数对刚性条形基础的动力柔度系数有较明显的影响。当基础摇摆的无量纲频率较小(b0<0.5)时，动力柔度系数实部受横观各向同性参数影响大，虚部受到的影响小；当基础摇摆的无量纲频率较大(b0>0.5)时，动力柔度系数实部受到横观各向同性参数的影响减弱，虚部受到的影响变大。此外，由式(19)可知，基底反力的合力与动力柔度系数成反比，故基础摇摆的频率对合力也会产生一定影响。而且横观各向同性参数取不同值时，动力柔度系数随基础摇摆的无量纲频率b0变化的规律相似，即：动力柔度系数实部随着无量频率的增加先增大后减小，并在无量纲频率b0=0.75附近达到峰值；而虚部的绝对值随着无量频率的增加而增加。

6 层状参数影响

三层地基的三种不同工况下的弹性参数取值见表1。其它参数取值为：n1=n2=n3=2，μvh1=μh1=μvh2=μh2=μvh3=μh3=0.25，Gv1=Gv2=Gv3=2 MPa；上两层地基厚度相等，最下层为半空间。地基动力柔度系数的计算结果见图6，由图6可以看出：对比工况1和工况2，土层一弹性模量增大时，基础动力柔度系数减小；对比工况2和工况3，地基上面两层土的平均弹性模量相同，而地基动力柔度系数曲线不同，并且工况3的上层土的弹性模量大，而其地基动力柔度系数的绝对值小。综上，其它条件相同的情况下，上层土的弹性模量对地基的动力柔度系数影响较大；并且上层土的弹性模量越大，地基的动力柔度系数的实部和虚部的绝对值越小。因此，对地基进行动力分析时，有必要考虑地基成层性的影响。

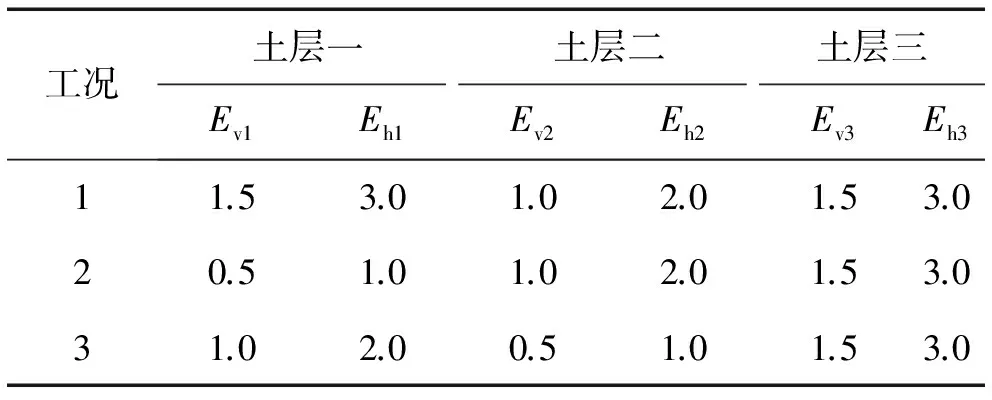
表1 计算工况一览

图6 地基成层性对地基动力柔度系数的影响

7 结 论

本文利用层状横观各向同性地基的解析层元解答，并结合刚性条形基础与地基接触的混合边值条件建立对偶积分方程，利用Jacobi正交多项式求解出地基的动力柔度系数。通过与文献结果的对比，说明了本文理论和数值计算方法的合理性。算例分析表明：土的横观各向同性性质和成层性对地基动力柔度系数产生了较大的影响，故在工程实践中有必要考虑两者的影响。

[1] LAMB H. On the propagation of tremors over the surface of an elastic solid[J]. Philosophical Transactions of the Royal Society of London Series A, 1904, 203: 1-42.

[2] 马晓华, 蔡袁强, 徐长节. 饱和地基上条形弹性基础的摇摆振动[J]. 岩土力学, 2010, 31(7):2164-2172.

MA Xiaohua, CAI Yuanqiang, XU Changjie. Rocking vibration of an elastic strip footing on saturated soil[J]. Rock and Soil Mechanics, 2010, 31(7): 2164-2172.

[3] 胡灿阳, 陈清军, 徐庆阳, 等. 埋置块式基础地基阻抗函数的简化计算方法研究[J]. 振动与冲击, 2011, 30(5):252-256.

HU Canyang, CHEN Qingjun, XU Qingyang, et al. Simplified calculation method for impedance function of embedded block foundation[J]. Journal of Vibration and Shock, 2011, 30(5): 252-256.

[4] STONELEY R. The seismological implication of aeolotropy in continental structures[J]. Geophysical Supplements to the Monthly Notices of the Royal Astronomical Society, 1949, 5(8): 343-353.

[5] KHOJASTEH A, RAHIMAIN M, PAK R Y S, et al. Asymmetric dynamic Green’s functions in a two-layered transversely isotropic half-space[J]. Journal Engineering Mechanics, 2008, 134(9): 777-787.

[6] KHOJASTEH A, RAHIMAIN M, ESKANDARI M, et al. Three-dimensional dynamic Green’s functions for a multilayered transversely isotropic half-space[J]. International Journal of Solids and Structure, 2011, 48(9): 1349-1361.

[7] AI Z Y, ZHANG Y F. Plane strain dynamic response of a transversely isotropic multilayered half-plane[J]. Soil Dynamics and Earthquake Engineering, 2015, 75: 211-219.

[8] AI Z Y, LI Z X. Time-harmonic response of transversely isotropic multilayered half-space in a cylindrical coordinate system[J]. Soil Dynamics and Earthquake Engineering, 2014, 66: 69-77.

[9] 何芳社, 黄义, 郭春霞. 横观各向同性饱和弹性半空间地基上圆环板的简谐振动[J]. 力学季刊, 2010, 31(1):124-130.

HE Fangshe, HUANG Yi, GUO Chunxia. Harmonic vibration of annular plates on transversely isotropic saturated porous half space[J]. Chinese Quarterly of Mechanics, 2010, 31(1):124-130.

[10] 马晓华. 饱和地基上条形基础的摇摆振动特性分析[D].杭州：浙江大学，2008.

[11] LUCO J E, WESTMANN R A. Dynamic response of a rigid footing bonded to an elastic half space[J]. Journal of Applied Mechanics, 1972, 39(2): 527-534.

[12] 肖仁成, 赵锡宏. 有限元和有限层元研究横向同性土对建筑物沉降的影响[J]. 岩土力学, 2007, 28(10):2133-2137.

XIAO Rencheng, ZHAO Xihong. Effect of transversely isotropic soil on settlement of buildings[J]. Rock and Soil Mechanics, 2007, 28(10):2133-2137.

Influences of layered transversely isotropy property of soils on rocking vibration of a rigid strip foundation

AI Zhiyong1, 2, REN Guangpeng1, 2

(1. Department of Geotechnical Engineering, Tongji University, Shanghai 200092, China; 2. Key Laboratory of Geotechnical and Underground Engineering of Ministry of Education, Tongji University, Shanghai 200092, China)

Influences of transversely isotropy and layered property of soils on rocking vibration of a rigid strip foundation were analyzed. The total stiffness matrix for the plane transversely isotropic layered soils was obtained by employing the analytical layer-element method. Based on the mixed boundary conditions of the contact problem, a pair of dual integral equations was established. Meanwhile, with the aid of Jacobi orthogonal polynomials, the dynamic compliance coefficients could be obtained. Numerical results were carried out by computer programs. The results agree well with the present theory and existing references. Further numerical examples show that with the decrease of the ratio of horizontal elastic modulus to vertical elastic modulus of soils, the dynamic flexibility coefficient is getting larger. It is also demonstrated that the increase of the ratio of vertical shear modulus to elastic modulus and the increase of the ratio of horizontal Poisson’s ratio to vertical Poisson’s ratio will lead to the increase of the dynamic flexibility coefficient. Moreover, the decrease of the elastic modulus of the upper soil will lead to the increase of the dynamic flexibility coefficient.

rocking vibration; layered soils; transverse isotropy; dual integral equation

2015-10-22 修改稿收到日期：2016-01-25

艾智勇 男，博士，教授，1966年生

TH212； TH213.3

A

10.13465/j.cnki.jvs.2017.08.009