钢-砼叠合边主梁斜拉桥稳定板气动措施研究

王嘉兴， 牛华伟， 靳俊中， 张志田， 陈政清

(1. 湖南大学 风工程与桥梁工程湖南省重点实验室, 长沙 410082；2. 河南省公路工程局集团有限公司, 郑州 450052)

钢-砼叠合边主梁斜拉桥稳定板气动措施研究

王嘉兴1， 牛华伟1， 靳俊中2， 张志田1， 陈政清1

(1. 湖南大学 风工程与桥梁工程湖南省重点实验室, 长沙 410082；2. 河南省公路工程局集团有限公司, 郑州 450052)

钢-砼叠合边主梁断面广泛应用于大跨径斜拉桥中，但该断面形式容易产生大幅涡激共振，颤振风速也较低，应用于沿海地区桥梁常常需要附加抑振气动措施。基于两座实际的斜拉桥工程方案，通过节段模型风洞试验，对稳定板气动措施的抑振效果进行了研究。结果表明,通过合理布置稳定板这类气动措施可以有效抑制边主梁断面涡激共振的发生，并且可以改善颤振性能，提高颤振临界风速。

斜拉桥； 边主梁； 气动措施； 稳定板； 风洞试验

近30年，我国交通事业飞速发展，桥梁建设规模及跨度已跃居世界前列。钢-砼叠合边主梁因自重较轻、受力合理、施工方便、综合效益高等特点[1-2]，近些年被广泛应用于大跨桥梁结构上，尤其是主跨度300～600 m的大跨斜拉桥上[3]。表1列举了国内部分叠合边主梁斜拉桥。

然而，钢-砼叠合梁斜拉桥常采用的边主梁断面的气动性能却不佳，在低风速下很容易发生涡激共振，颤振临界风速也比较低[4]。尤其在沿海地区，这一类型断面常常无法达到设计要求，需要采用合适的抑振措施来改善气动性能。其中，气动措施通过改变桥梁断面绕流形态来达到抑振效果，因构造简单，经济实用等优点而被经常用于实际工程的设计中。气动措施有导流板、抑流板、风嘴、稳定板等形式[5-7]。不同断面形状的主梁气动性能不同，采取的气动措施也往往不同[8](见表1)。目前，在设计中一般通过风洞模型试验来选取理想的气动措施[9-10]。

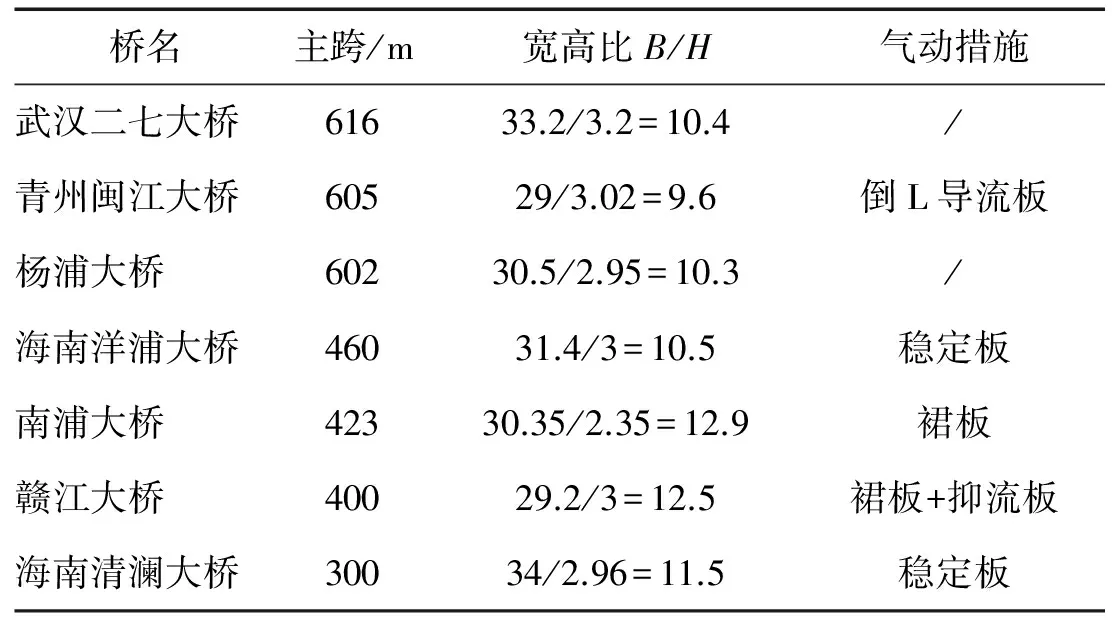
表1 国内典型叠合边主梁斜拉桥列表

相关试验表明，在开口边主梁断面的顶板下部合理设置稳定板可以破坏主梁下部漩涡的形成，从而达到抑制风振的目的。本文将分别以工字型和箱型两种常用的边主梁形式为基础，结合两座实际桥梁的设计方案研究稳定板气动措施的性能与设置方式以供桥梁设计参考。

1 试验概况

1.1 工程背景

桥例一位于海南省文昌市，是一座跨越海湾的大跨度桥梁，主桥为双塔三跨斜拉桥，其跨径布置为(124+300+124)m。主梁采用钢-砼叠合梁形式，由左右钢箱梁、钢横梁以及混凝土桥面板组成，横断面宽34 m，高2.96 m，宽高比(B/H)为11.5。其初始设计方案如图1所示。

图1 桥例一初始设计方案断面图(m)

桥例二连接海南省洋浦经济开发区和儋州白马井镇。大桥主桥为双塔双索面混合式叠合梁斜拉桥，结构体系采用空间索面半漂浮体系。主桥的跨径布置为(58.5+63+58.5+460+58.5+63+58.5)m，其中主跨中间440 m梁段为工字钢叠合梁，主跨两端各10 m及边跨为混凝土边主梁。钢-砼叠合边主梁断面宽31.4 m，中央高3 m，宽高比(B/H)为10.5，其初始设计方案如图2所示。

图2 桥例二初始设计方案断面图(m)

1.2 试验主要参数

节段模型弹性悬挂风洞试验在湖南大学风工程试验中心HD-2号风洞高速试验段中进行，试验段断面尺寸为3.0 m(宽)×2.5 m(高)，试验段长17 m，风速在0～58 m/s连续可调。均匀流场紊流度在1.0%以下，来流俯仰角小于0.5°，偏航角小于1°，各项均满足规范[11]中的风洞试验要求。桥例一和桥例二节段模型分别采用几何相似比λ=1∶50和1∶60，根据测振节段模型相似性要求设计，主要参数见表2。节段模型见图3。

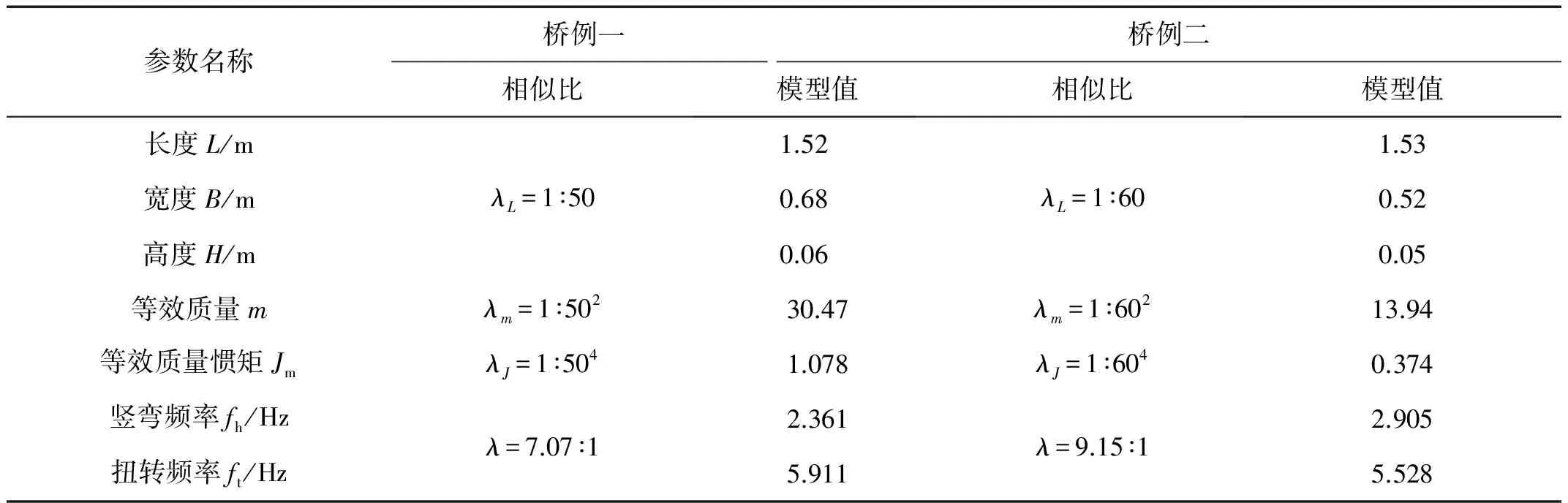
表2 节段模型主要参数

图3 风洞中的节段模型

2 气动措施风洞试验研究

2.1 桥例一气动措施研究

试验在均匀流场中进行，风洞阻塞比小于5%。风攻角设置为0°，±3°。桥例一节段模型测试了多种阻尼工况，见表3。

将试验结果按照相似比和如下方法换算成实桥值以便直观地与其他桥梁比较。由于模型发生涡激共振时运动位移为振幅稳定的类正弦曲线。因此模型位移极大值即幅值与均方根值之间的关系为

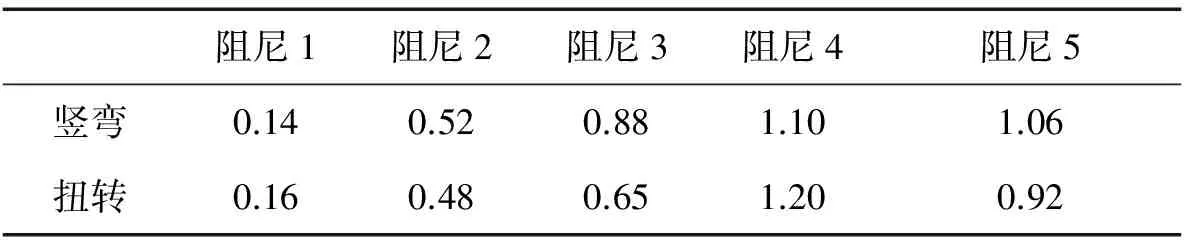
表3 桥例一模型阻尼比

(1)

式中:dm为节段模型位移幅值;dstd为节段模型位移均方差。

再根据文献[12]中所讨论的非线性涡激力模型下节段与全桥的振幅关系得到：

(2)

式中:ym为主梁最大位移振幅;φ(x)为主梁的振型函数并假定主梁振型为简谐函数;φmax(x)为振型最大幅值。

桥例一初步方案在成桥状态0°风攻角下的风洞试验结果如图4。结果表明桥例一的原设计断面，在实桥风速达到17 m/s左右时开始发生竖向的涡激共振，在12 m/s左右时开始发生扭转涡激共振。根据文献[11](简称《中国规范》)，涡振幅值远大于规范允许值。并且在阻尼比加大到规范建议取值为1%(阻尼比4)的情况下，扭转振动幅值仍然大于规范允许值，所以原设

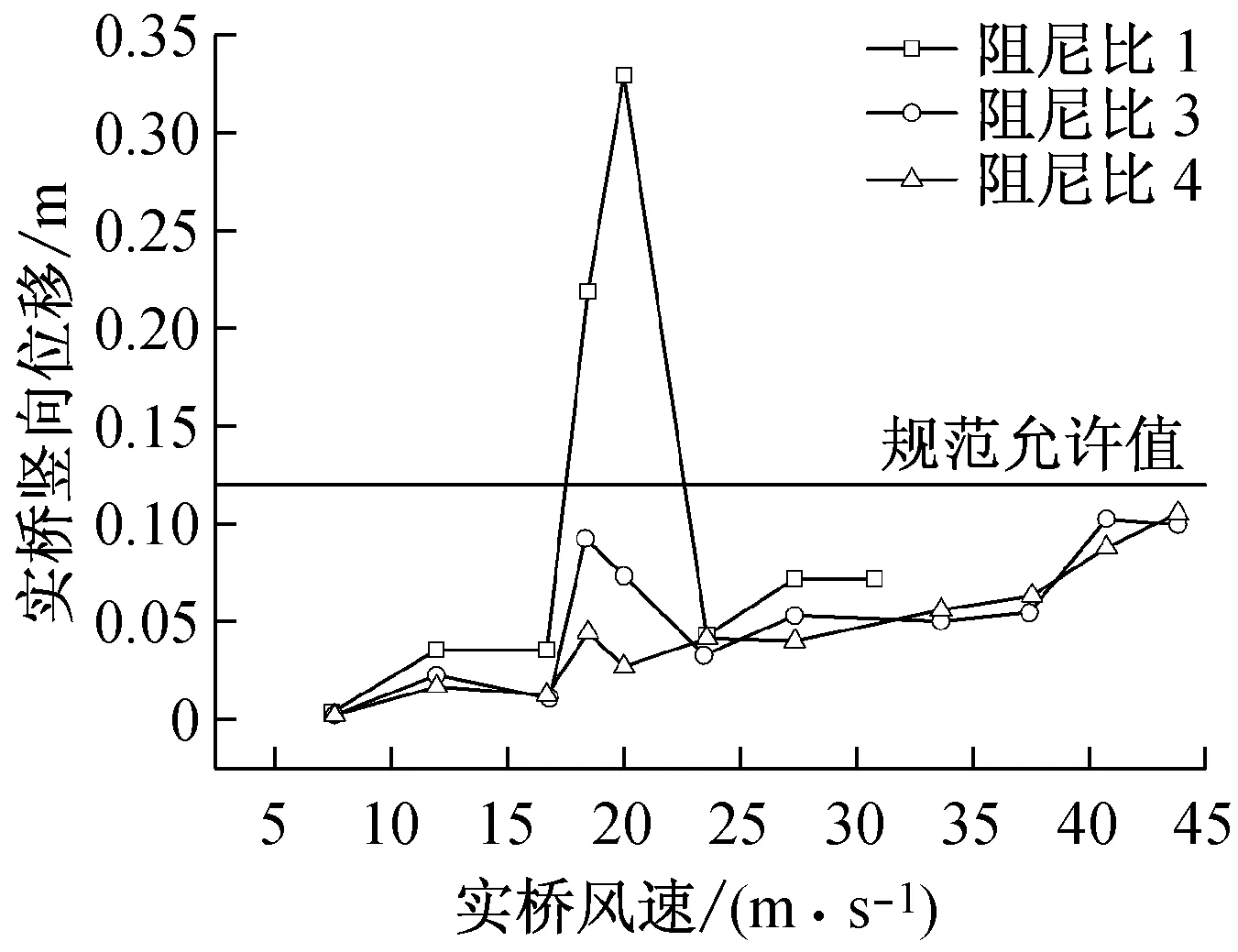
(a) 竖向位移幅值

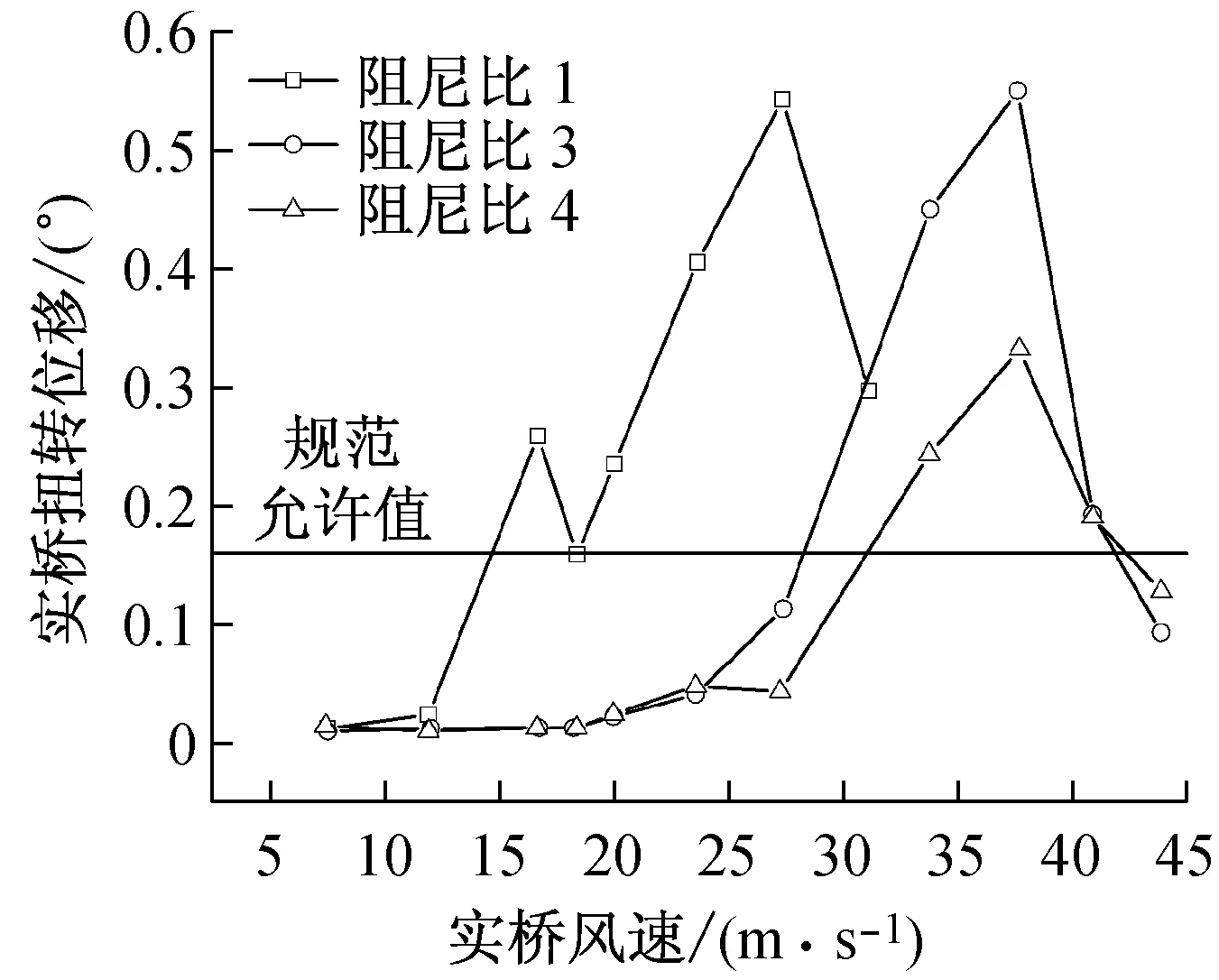
(b) 扭转位移幅值

计断面的气动稳定性不满足要求，需要设置气动稳定措施以改善主梁结构的气动性能。

试验共测试了四种措施多个工况下主梁的振动响应，振动信号采用加速度传感器测试竖向和扭转振动响应。措施的具体描述见表4，试验采用的阻尼比见表3。

由于国内规范尚没有对主梁涡振的加速度进行评价，故将《中国规范》位移幅值按类正弦曲线计算得到对应的加速度幅值，并参考文献[13](简称《英国法则》)中对于主梁涡振特性的评价标准。其中，英国桥梁设计实践中倾向于将实桥风速20 m/s范围内主梁加速度等于0.4 m/s2(0.04g)定为涡振限值[14]。

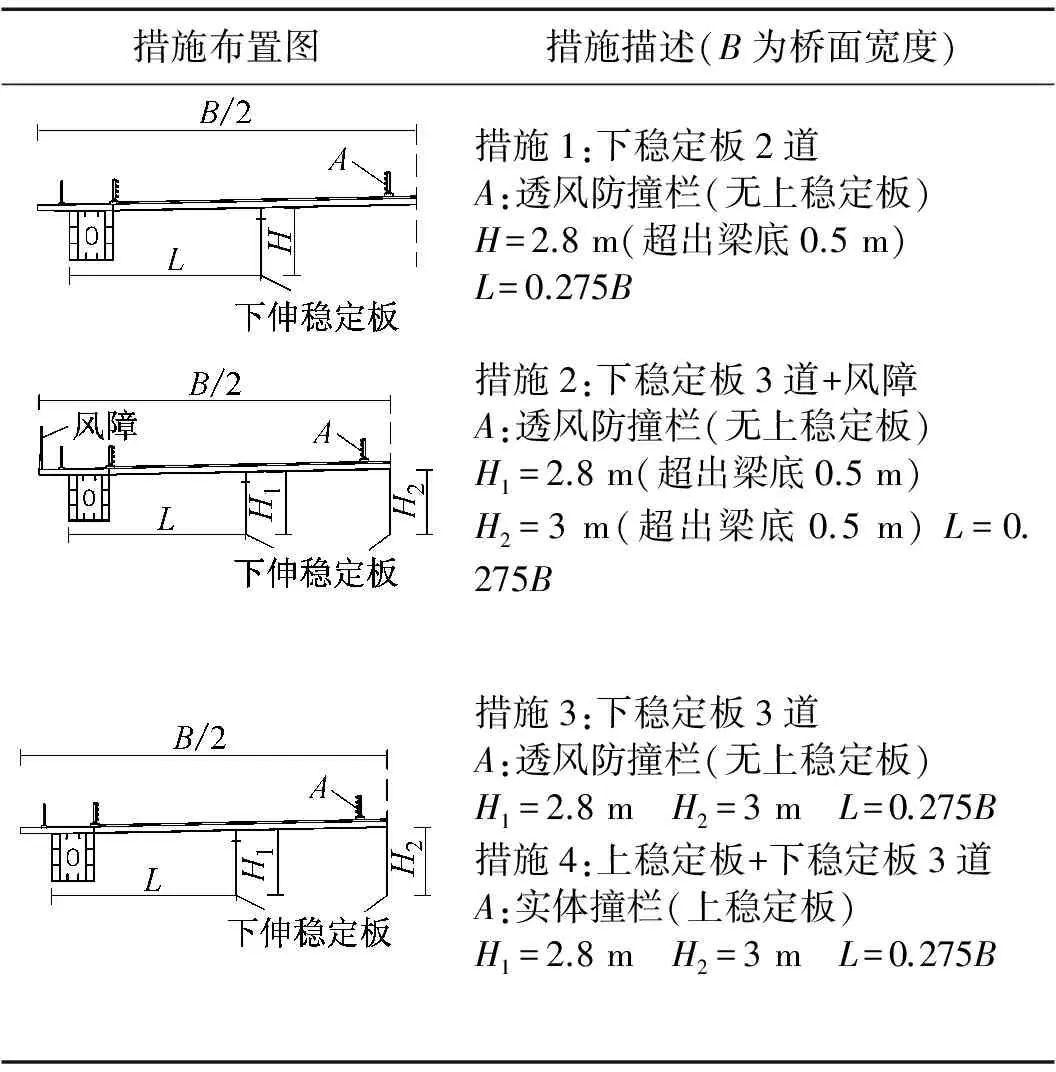
表4 桥例一气动措施表

图5(a)、(d)表明，在低阻尼比的情况下原设计断面采用措施1、2、3都有效地抑制了竖向涡振的发生，但均未有效抑制住扭转涡振。其中，措施2(三道下稳定板+风障)的第二个扭转涡振区间的振幅比原设计断面更为明显。比较可见，措施3即设置三道下稳定板的抑振效果相对较好。

对措施3进一步试验，随着阻尼比增大，涡振的幅值减小，如图5(b)、(e)所示。同时可见在+3°、0°和-3°风攻角中，+3°攻角是最不利风攻角，其涡振幅值明显大于其他风攻角。措施3(三道下稳定板)在阻尼比达到阻尼2时便可以抑制0°攻角下涡振的发生，达到阻尼3时便可抑制0°攻角及-3°攻角下涡振的发生，但是三道下稳定板没有在大阻尼比(阻尼比4)的情况下抑制+3°风攻角下的涡激共振。

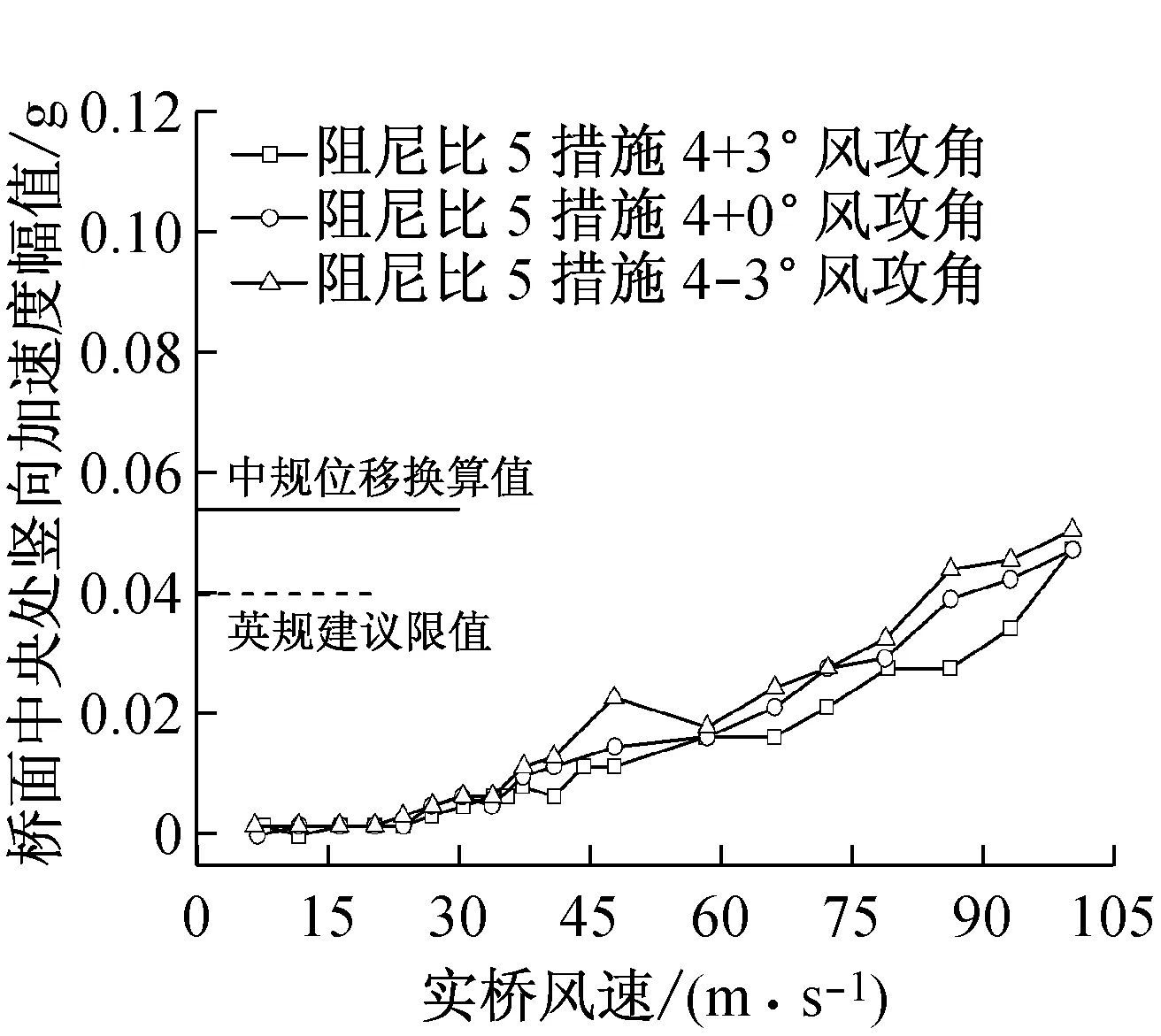
图5(c)、(f)中措施4(3道下稳定板+中央不透风栏杆形成上稳定板)基本抑制涡振的发生，并且颤振临界风速也满足要求，仅在+3°风攻角对应实桥风速值为35.64～40.87 m/s时出现了不稳定的扭转涡振，截面边缘振动的加速度最大值为0.06 g。对于实桥风速超过20 m/s，考虑到英规是针对舒适性因素故此限值应予以放宽[14]，此处应作为符合要求。而且，经测试得到的主梁最大涡振响应的幅值满足中国规范(文献[11])限值(如表5所示)，因此该方案是可行的。

(a) 不同措施桥面中央竖向振动

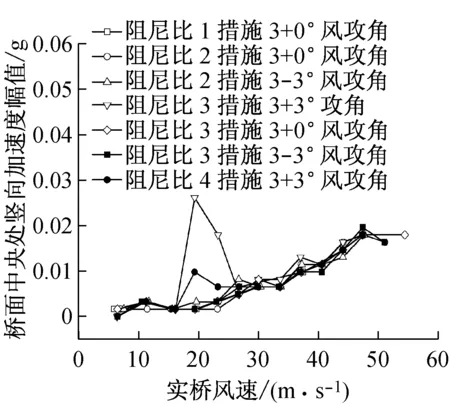
(b) 措施3桥面中央竖向振动

(c) 措施4桥面中央竖向振动

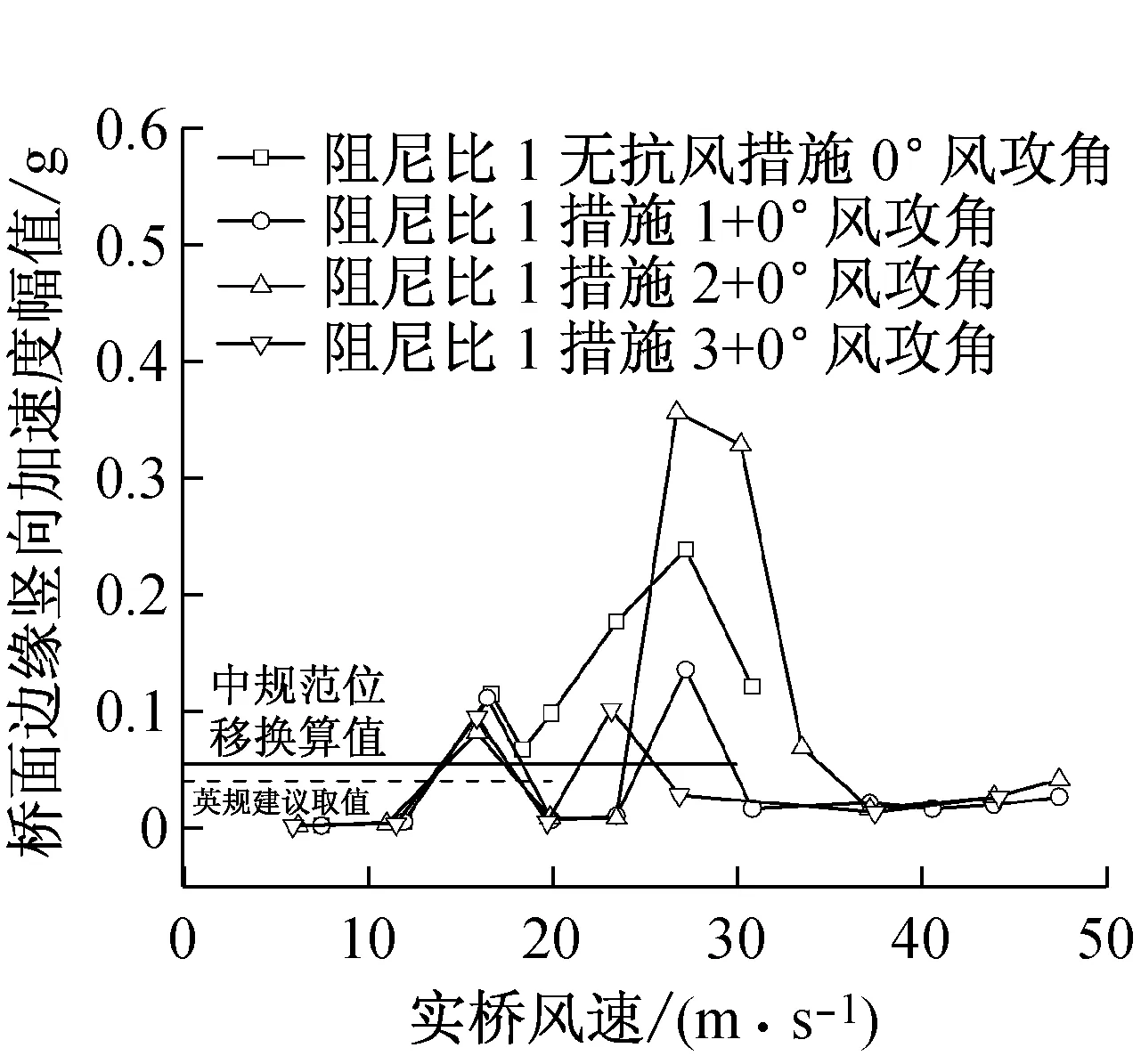
(d) 不同措施桥面边缘竖向振动

(e) 措施3桥面边缘竖向振动

(f) 措施4桥面边缘竖向振动

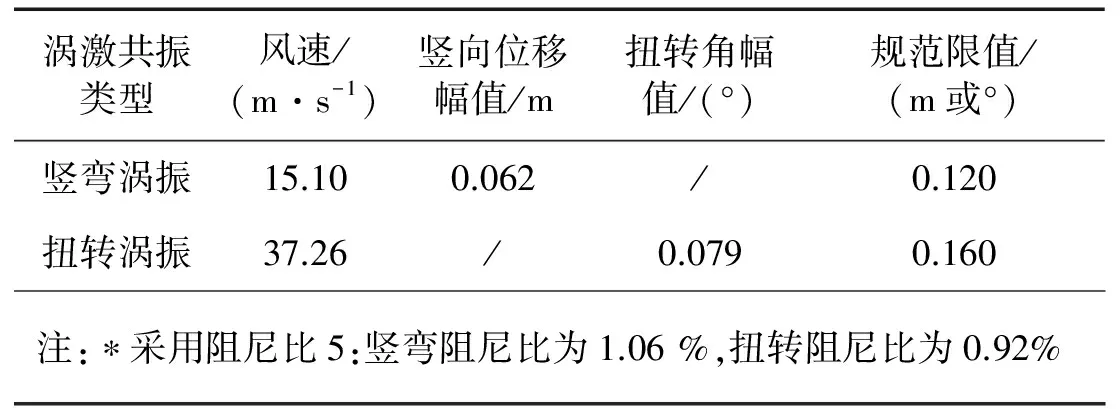
表5 桥例一推荐方案主梁最大涡振响应

横向对比这几种措施，可将其涡振抑制效果从好到差依次排列：措施4>措施3>措施1>措施2。比较措施3、措施1及无措施，可见一定范围内，合理布置的下稳定板数目越多，抑振效果越好。

2.2 桥例二抗风措施测试

根据规范(文献[11])条文说明中对实际斜拉桥的现场测试的统计结果，对于跨度450 m左右的叠合梁斜拉桥的阻尼比约在0.8%左右。故将桥例二阻尼比定在0.8%左右，控制竖弯振动阻尼比在0.75%～0.8%，扭转阻尼比在0.6%左右，略低于规范的建议值1.0%。测试风攻角为0°，±3°，并采用激光位移计采集振动信号。

由于涡激共振对主梁形状很敏感，在桥例二原设计方案上做了改变附属设施的工况试验，但试验结果(图6(a)、(d))表明，无论是采用混凝土防撞栏还是钢防撞栏，原设计断面在成桥状态+3°风攻角下，都会在实桥风速达到20 m/s时开始发生竖向涡激振动，最大幅值远大于规范允许值。并且，颤振风速为60 m/s，远低于规范要求的78 m/s的颤振检验风速。在无检修道的情况下也同样发生了明显的涡激共振和颤振，可见改变这些基本的附属设施对该桥断面的涡激共振影响甚微。因此，需要增加气动措施来抑制涡振同时又必须提高颤振稳定性。

基于桥例二原设计断面的六种措施方案(见表6)测试了多种工况下主梁的气动性能。风洞试验结果如图6所示，图中幅值为换算后的实桥幅值。

表6 桥例二措施表

试验结果图6(b)、(e)表明,仅采用措施1(中央上稳定板)在+3°风攻角下存在非常严重的竖向涡激共振现象，并且在实桥风速60 m/s时结构仍然扭转振动发散，可见仅仅设置上稳定板对颤振稳定性影响十分有限，对涡振抑制也没有明显的效果。

采用了措施2(上稳定板+1道下稳定板)的主梁节段在-3°风攻角实桥风速20～26 m/s内发生了非常明显的扭转涡激共振响应，如图6(f)中所示，扭转振幅远大于规范允许值，同时该工况下主梁的颤振风速为73.5 m/s，低于设计要求的颤振检验风速。

0°风攻角下的各气动措施方案均未发生振动，故不赘述。试验结果反应，该断面最不利风攻角为-3°。图6(f)可见，采用措施3(3道下稳定板)无法使颤振临界风速达到检验风速，但是相比原设计，颤振临界风速已经明显提高了。

措施5(上稳定板+2道设置距边缘1/3桥宽处的下稳定板)有效抑制了涡激共振的发生，但颤振临界风速仍不能满足规范要求。

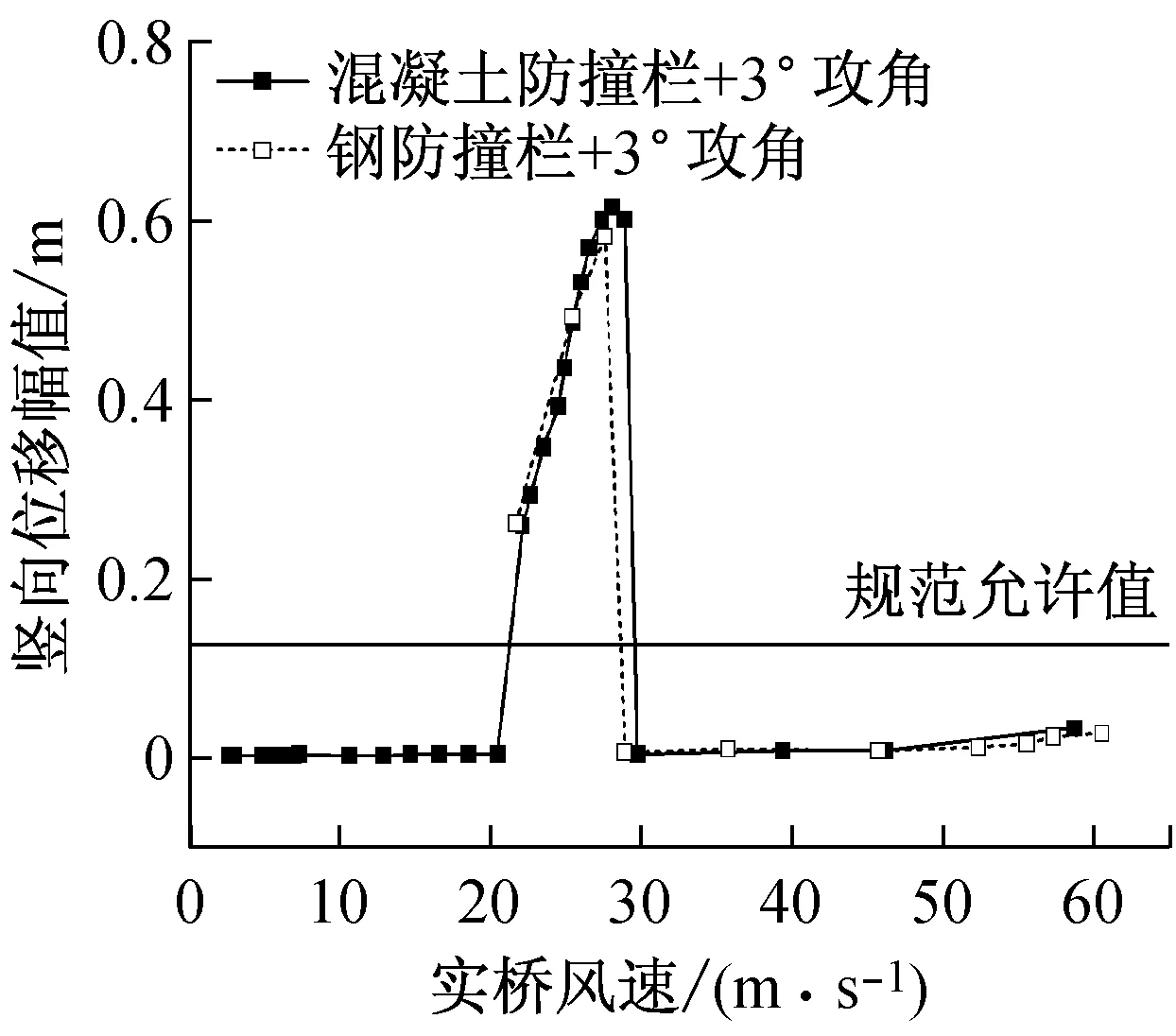
(a) 原设计的竖向位移幅值

(b) +3°各措施的竖向位移幅值

(c) -3°各措施的竖向位移幅值

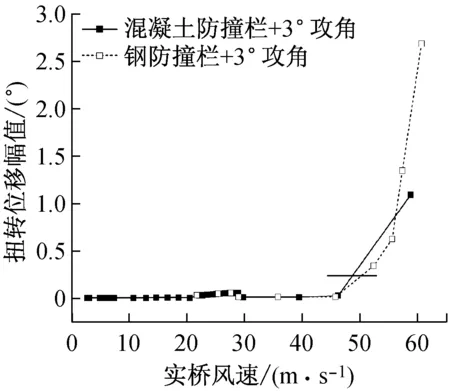
(d) 原设计的扭转位移幅值

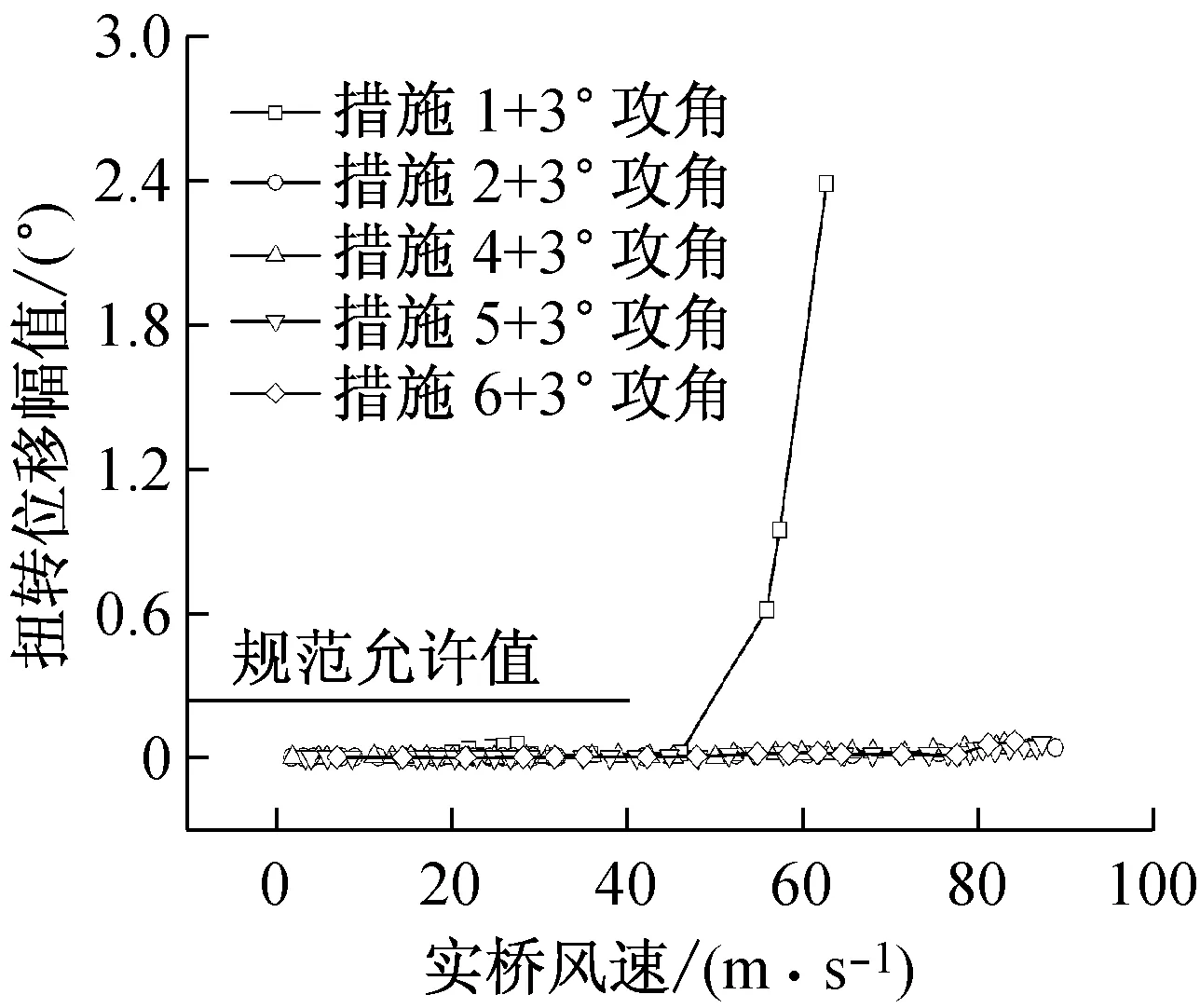
(e) +3°各措施的扭转位移幅值

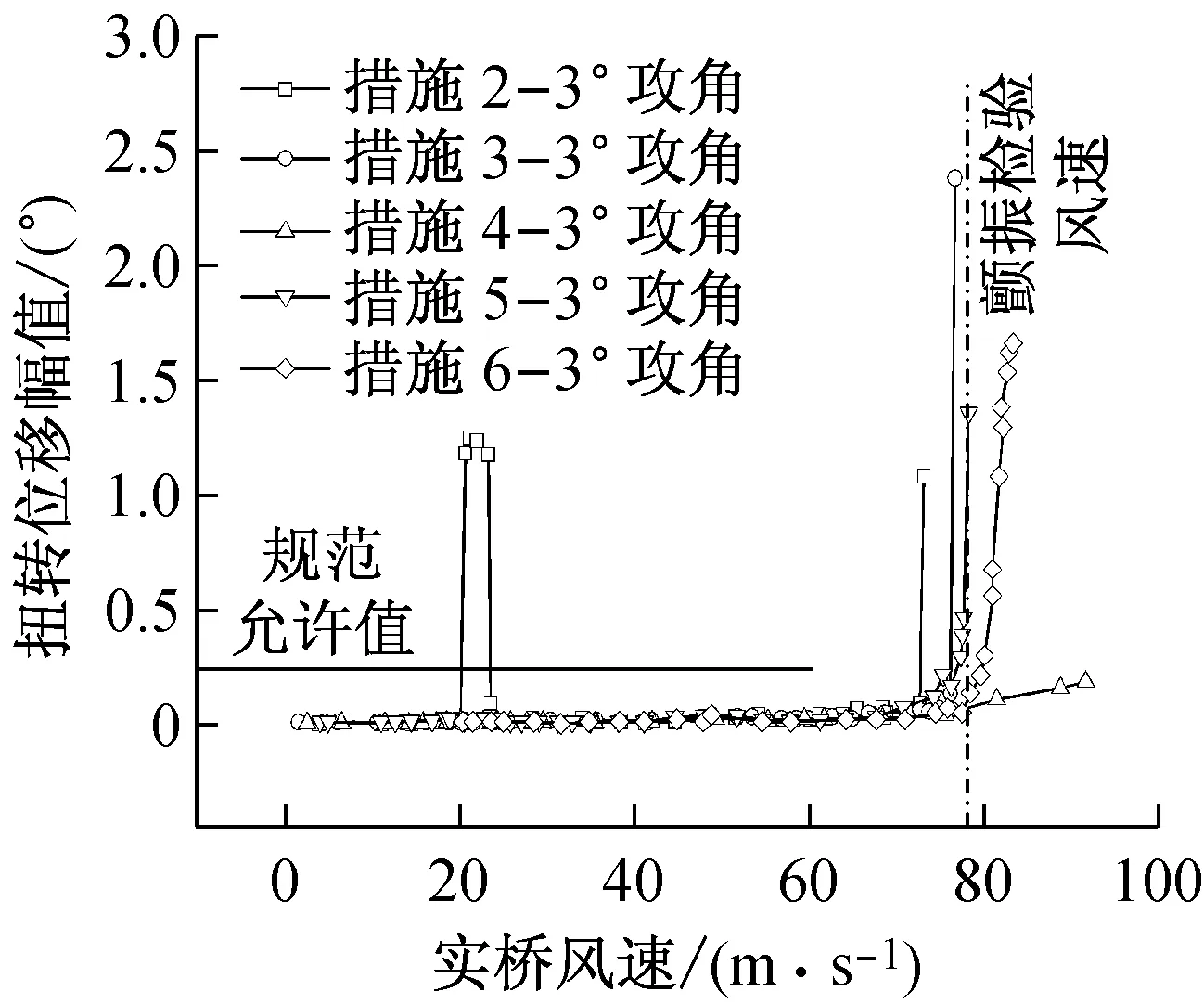
(f) -3°各措施的扭转位移幅值

图6(b)、(e)、(c)、(f)表明，措施4(中央上稳定板+3道下稳定板)和措施6(中央上稳定板+下稳定板2道)有效改善了实桥的气动性能，避免了成桥阶段的涡激共振现象，而且提高了设计结构的颤振稳定性，使之颤振临界风速在测试风攻角下从60 m/s提高到了80 m/s以上，高于该桥的颤振检验风速。但后者要更为经济，所以作为推荐方案。

通过对比措施1和措施2、4、5、6在+3°风攻角的试验结果，可见设置下稳定板有效地抑制了+3°风攻角下竖向涡激共振发生，对比措施2和措施3、4、5、6在-3°风攻角的试验结果，可见下稳定板有效地抑制了该风攻角下的扭转涡激共振。并且，下稳定板对提高颤振稳定性也起到了很大作用。

比较措施5和措施6两种方案，可见稳定板的位置也能影响颤振稳定性。综合比较这几种措施对颤振稳定性的优化程度：措施4>措施6>措施5>措施3>措施2。可见，在一定范围内，合理布置的下稳定板的数目越多，颤振稳定性越好。

2.3 St数的变化

斯托罗哈数(Strouhal number，St数)就是描述钝体漩涡脱落规律的无量纲数：

(3)

式中：fs为涡激共振起振时漩涡脱落的频率；U为涡激共振起振时的风速；D为特征尺寸，取梁高。

由式(3)可知，St数越大，发生涡激共振的风速越低，可能性也越大。

表7、8列出了桥例一和桥例二原型断面及出现了涡振的气动措施方案的St数。从中可见，不同的风攻角下，St数也会不同。桥例一存在两个扭转涡振区间。根据一些对双竖向涡振的研究，可以推断同样可能是主梁在高低不同风速下，在不同部位形成各自独立的旋涡脱落，从而引起的主梁涡振。

表7 竖向涡振的St数

表8 扭转涡振的St数

3 结 论

本文对两座典型叠合边主梁断面桥梁进行了刚性节段模型风洞试验，测试了不同阻尼比下多种稳定板抗风措施方案的振动响应，对比分析了这些抗风措施的抑振效果，得到的主要结论如下：

(1) 叠合边主梁断面在风速不高的情况下容易发生大幅涡振，并且在阻尼比达到允许值时，主梁断面的涡激共振仍然没有被有效抑制。所以桥例一及桥例二主梁断面都需要增加抑振措施。

(2) 试验表明，随着阻尼比的提高，涡振振幅降低，在一定范围内风速锁定区间不会明显改变，这与以往一些试验结果也是相符的。

(3) 桥例一和桥例二在一定范围内增设布置合理的下稳定板可以减小涡振，提高颤振稳定性，数目越多，效果越明显。同时，稳定板设置的位置也将影响桥梁断面的气动性能。

(4) 合适的上、下稳定板的组合措施能有效抑制桥例一和桥例二的涡激共振，并且对提高颤振稳定性也作用明显。然而，不当的稳定板措施也可能增大涡振振幅，降低涡振起振风速。文中的方案可供类似桥梁参考。

[1] DAITO Y, MATSUMOTO M, ARAKI K. Torsional flutter mechanism of two-edge girders for long-span cable-stayed bridge[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2002, 90(12): 2127-2141.

[2] 宋锦忠，哈鸿，毛鸿银． 开口主梁断面的气动选型[C]∥第五届全国风工程及工业空气动力学学术会议论文集． 张家界，1998: 240 -245．

[3] 宋锦忠,林志心,徐建英.桥梁抗风措施的研究及应用.同济大学学报, 2002,30(5):618-621.

SONG Jinzhong, LIN Zhixin, XU Jianying. Research and appliance of aerodynamic measures about wind-resistance of bridges[J].Journal of Tongji University, 2002, 30(5): 618-621.

[4] 杨詠昕，周锐，葛耀君. 大跨度桥梁实用颤振控制方法[J]. 同济大学学报(自然科学版), 2014, 42(7): 989-997.

YANG Yongxin, ZHOU Rui,GE Yaojun.Practical flutter control method for long-span bridges[J].Journal of Tongji University(Natural Science), 2014, 42(7): 989-997.

[5] 陈政清．桥梁风工程[M]．北京：人民交通出版社，2005：129-130.

[6] 胡长灿，詹昊.大跨度桥梁抗风设计常用气动措施分析[J].桥梁建设, 2015,45(2):77-82.

HU Changcan，ZHAN Hao.Analysis of common aerodynamic measures for wind resistant design of long span bridges[J].Bridge Construction, 2015,45(2):77-82.

[7] 刘建新.桥梁对风反应中的涡激振动及制振[J].中国公路学报，1995，8(2)：74-79．

LIU Jianxin. Vortex induced vibration and its control in responses of bridge to wind[J]. China Journal of Highway and Transport, 1995,8(2):74-79.

[8] SARWAR M W，ISHIHARA T． Numerical study on suppression of vortex-induced vibrations of box girder bridge section by aerodynamic countermeasures[J]．Journal of Wind Engineering and Industrial Aerodynamics，2010，98(12)：701-711．

[9] 董锐，杨詠昕，葛耀君.斜拉桥Π型开口断面主梁气动选型风洞试验[J]. 哈尔滨工业大学学报,2012,44(10):109-114.

DONG Rui，YANG Yongxin，GE Yaojun.Wind tunnel test for aerodynamic selection of Π shaped deck of cable-stayed bridge[J]. Journal of Harbin Institute of Technology, 2012,44(10):109-114.

[10] 徐泉，王武刚，廖海黎，等． 基于大尺度节段模型的悬索桥涡激振动控制气动措施研究[J]． 四川建筑，2007，27(3)：110-112.

XU Quan，WANG Wugang，LIAO Haili，et al. Study the aerodynamic control measures for vortex-induced vibration based on a large scale section model of a suspension bridge[J].Sichuan Architecture,2007,27(3):110-112.

[11] 公路桥梁抗风设计规范：JTG/T D60-01—2004[S]. 北京：人民交通出版社，2004.

[12] 张志田,陈政清. 桥梁节段与实桥涡激共振幅值的换算关系[J].土木工程学报,2011,44(7):77-82.

ZHANG Zhitian, CHEN Zhengqing. Similarity of amplitude of sectional model to that of full bridge in the case of vortex-induced resonance[J].China Civil Engineering Journal,2011,44(7):77-82.

[13] Design Rules for Aerodynamic Effects on Bridges: BD 49/01[S].

[14] 陈政清，黄智文.大跨度桥梁竖弯涡振限值的主要影响因素分析[J].中国公路学报,2015,28(9):30-36.

CHEN Zhengqing, HUANG Zhiwen. Analysis of main factors influencing allowable magnitude of vertical vortex-induced vibration of long-span bridges[J].China Journal of Highway and Transport,2015,28(9):30-36.

Study on stabilizer aerodynamic measure of a cable-stayed bridge with a steel-concrete composite edge girder

WANG Jiaxing1, NIU Huawei1, JIN Junzhong2, ZHANG Zhitian1, CHEN Zhengqing1

(1. Hunan Provincial Key Laboratory for Wind Engineering and Bridge Engineering, Hunan University, Changsha 410082, China;2. Henan Province Highway Engineering Bureau Group Co. Ltd., Zhengzhou 450052, China)

A steel-concrete composite edge girder is widely used in a long-span cable-stayed bridge, but it frequently leads to remarkable vortex-induced vibration and low flutter critical wind speed. Therefore, aerodynamic measures are always needed to improve the aerodynamic performance when this type of bridge is built in coastal region. Based on two cable-stayed bridges with steel-concrete composite edge girder, the controlling effect of stabilizer on the steel-concrete composite girder was investigated with a series of sectional model wind tunnel tests. The results indicate that the stabilizer can effectively eliminate vortex-induced vibration and increase the flutter critical wind speed of the edge girder section.

cable-stayed bridge; edge girder; aerodynamic measure; stabilizer; wind tunnel test

同济大学桥梁结构抗风技术交通行业重点实验室开放课题基金(KLWRTBMC)； 湖南省高校创新平台开放基金(14K021)

2016-01-26 修改稿收到日期：2016-03-24

王嘉兴 男，硕士,1990年8月生

牛华伟 男，博士，硕士生导师，1978年9月生

U443.3

A

10.13465/j.cnki.jvs.2017.08.008