RST数字控制器及其在时延系统中的应用

李明辉 宋忠柱 徐文力 谭礼斌 李光辉

(陕西科技大学机电工程学院,陕西西安,710021)

RST数字控制器及其在时延系统中的应用

李明辉 宋忠柱*徐文力 谭礼斌 李光辉

(陕西科技大学机电工程学院,陕西西安,710021)

RST数字控制器是一个三支路结构控制器,可以等效为一个前向预测器和一个无时延的控制器,能够很好地解决时延系统中的相位变化问题,使系统具有较好的鲁棒性。PID控制器、PID-Smith预估控制器和RST数字控制器的仿真实验表明,在这3种控制器中,RST数字控制器的跟踪性能和抑制扰动性能最好,而且对于参数不定的系统,其还具有较强的鲁棒性。

RST数字控制器；时延系统；相位；鲁棒性

长久以来,数字控制理论一直受制于连续控制理论的发展,数字控制器的设计被认为是模拟数字控制器的数字化而已[1]。随着计算机的快速发展,各种微型计算器功能越来越强大,复杂的数字控制算法能够直接在硬件上运用,并且体现出了许多模拟控制器无法企及的优越性。

时延系统在造纸生产中比较常见。时延的存在导致了与频率成正比的相位变化,故利用传统的控制策略很难得到满意的控制性能[2]。对时延系统的研究方兴未艾,目前,比较流行的控制策略主要有：Smith预估器控制、IMC内膜控制和模糊智能控制,以及这些控制策略的改进型[3- 4]。以上每种方法在标称条件下均能获得理想的控制效果,但是,控制器的控制性能依赖于模型的准确程度,所以鲁棒性能较差；此外,这些控制策略是为连续时间系统设计的,所以实际应用时要进行离散化处理,这会造成离散化的控制器无法达到原来的控制性能。因此,有必要引入一种鲁棒性强且能直接应用于实际的控制器,这就是RST三支路数字控制器的由来[5- 6]。

1 数字控制器结构

1.1 常见数字控制器结构

常见的数字控制系统主要包括：数字控制器(Digital Controller)、同步时钟(Clock)、零阶保持器(ZOH)、执行器、过程、传感器及DAC(数模转换器)和ADC(模数转换器)等。对象的输出信号y(t)为连续时间信号,经过同步时钟和ADC转换变为离散值y(k),y(k)再与设定值比较,得到偏差e(k),进入数字控制器后调用具体的算法计算出控制量u(k),最后通过零阶保持器重新变为连续时间变量u(t)输入到执行器(见图1)。

1.2 RST数字控制器结构

RST数字控制器是一个三支路数字控制器,结构如图2所示,3个支路分别用R(q-1)、S(q-1)和T(q-1)表示,它们都由多项式来代替,设置不同的多项式系数可以得到不同控制特点的控制器。

控制信号：

(1)

开环传递函数：

(2)

输入到输出的闭环传递函数：

(3)

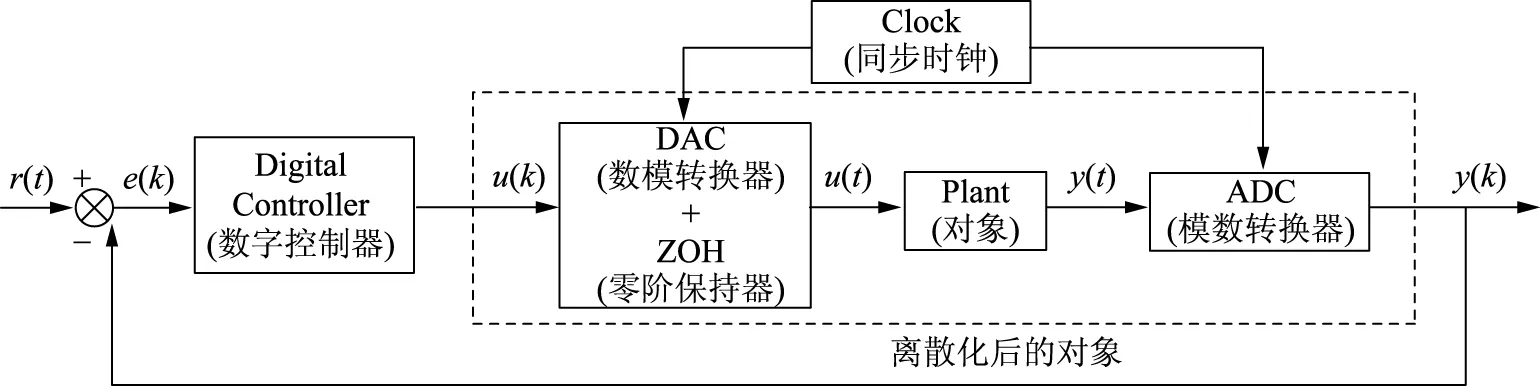
图1 RST数字控制器设计

图2 RST数字控制器结构

引入如下公式：

A(q-1)=1+a1q-1+…+anAq-nA=

1+q-1A*(q-1)

(4)

A*(q-1)=a1+a2q-1+…+anAq-nA+1

(5)

B(q-1)=b1q-1+b2q-2+…+bnBq-nB=

q-1B*(q-1)

(6)

B*(q-1)=b1+b2q-1+b3q-2+…+bnBq-nB+1

(7)

S(q-1)=1+s1q-1+…+snSq-nS=

1+q-1S*(q-1)

(8)

R(q-1)=r0+r1q-1+…+rnRq-nR

(9)

系统的特征多项式为：

P(q-1)=A(q-1)S(q-1)+q-dB(q-1)R(q-1)=1+p1q-1+p2q-2+…

(10)

多项式P(q-1)是闭环传递函数的分母项,定义了系统的极点,同时也决定了闭环系统的动态响应性能,因此,可以将多项式P(q-1)的系数看作系统性能指标的体现。

2 RST数字控制器参数设计

设计RST数字控制器最主要的就是确定参数,具体来说,就是确定R(q-1)、S(q-1)和T(q-1)的多项式系数,其中,T(q-1)的引入增加了系统的自由度,从而可以设计出同时满足跟踪性能和抑制干扰性能的数字控制器,这也是RST数字控制器具有良好鲁棒性的重要体现。控制参数设计的具体步骤如下。

(1)获得对象模型,并进行离散化处理。

对象模型的获取至关重要,模型越准确,控制器的设计越有针对性,控制效果也就越好。一般来说,对象模型的获取有2种：一种是通过机理分析,建立对象的微分方程,做拉氏变换得到对象的传递函数；另一种是通过实验法,由测试数据辨识出系统对象模型[7]。第一种方法局限性较大,对于稍微复杂的对象就很难通过机理分析得到数学模型。第二种方法应用范围较广,其辨识方法又可以分为：基于白化预测误差的辨识方法和基于观测向量和预测误差的不相关性的辨识方法[8]。用于系统辨识的软件有WinPIM+和MATLAB系统辨识工具箱。

针对RST数字控制器来说,对象模型用式(11)多项式来表示。

总而言之,在急性颅脑损伤诊断过程中,MRI成像具有较高的诊断准确率和分别率,其能够及早的将颅脑损伤病灶显示出来,为急性颅脑损伤的诊断和治疗奠定基础,值得进一步采纳和推广。

(11)

通过模型辨识得到的传递函数经过离散化处理后得到上述模型,其包括3个部分,即时延部分、离散所得分子项和分母项。

(2)选择闭环极点,确定多项式P(q-1)。

方法一：根据理想性能指标,确定多项式P(q-1)。

令：P(q-1)=1+p1q-1+p2q-2,由u(t)=P(q-1)y(t)得

y(t+2)=-u(t+2)-p1y(t+1)-p2y(t)

(12)

当输入为0时,求系统的自由输出响应。令：p1=-0.75、p2=0,可以得到y(t+1)=0.75y(t),即对象输出在下一时刻衰减到75%；对于一个稳定的系统来说,p1应为负值,且其绝对值应小于1。

方法二：对于一个二阶系统来说,可以通过指定上升时间、调节时间和最大超调量来确定系统的自然频率和阻尼比,从而得到二阶系统的传递函数,加上零阶保持器后再进行离散化,得到的传递函数的分母就是多项式P(q-1),进而得到系数p1和p2。例如,带零阶保持器的连续时间系统模型：

(13)

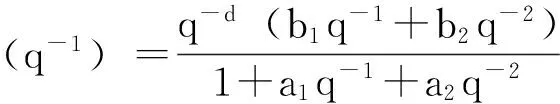
(14)

则p1=a1,p2=a2。

(3)解Bezout多项式等式,并求出R(q-1)、S(q-1)和T(q-1)。

有3种方法可以求解RST数字控制器的参数：极点配置法、独立目标的跟踪和调节法和基于内膜的跟踪和调节控制；实际上后2种方法也是极点配置法。极点配置中求解Bezout等式是RST数字控制器参数设计中最主要的一个步骤。经过前2个步骤,已经得到A(q-1)、B(q-1)和P(q-1),但是R(q-1)和S(q-1)还不确定,求Bezout等式的过程其实就是确定多项式R(q-1)和S(q-1)的系数的过程。Bezout等式如下：

P(q-1)=A(q-1)S(q-1)+q-dB(q-1)R(q-1)

(15)

当且仅当A(q-1)和B(q-1)互质时等式有唯一解,此时应满足：

nP=degP(q-1)≤nA+nB+d-1

(16)

nS=degS(q-1)≤nB+d-1

(17)

nR=degR(q-1)=nA-1

(18)

式(17)和式(18)中,R(q-1)和S(q-1)的阶数nS、nR不包含预先指定的因子项。

为了便于利用计算机进行求解,将未知参数写成一个列向量,特征多项式P(q-1)的系数也写成一个列向量,得到如下的矩阵：

Mx=p

(19)

其中,xT=[1,s1,…,sns,r0,…,rnR]；pT=[1,p1,…,pnp,0,…,0],关系矩阵M如下。

等式两边对关系矩阵求逆运算,得到：

x=M-1p

(20)

所以,可以求出R(q-1)和S(q-1)。

求解等式时,可以事先指定R(q-1)和S(q-1)的某些因子项,例如,当考虑到系统稳态误差和抑制扰动时,S(q-1)的多项式应该包括因子项(1-q-1),以保证闭环系统稳态增益等于1,该因子项的作用相当于在前向通道中加入一个积分器。

T(q-1)的确定与系统的跟踪控制性能有关。通过期望性能指标事先指定一个跟踪模型,当参考输入发生变化时,使系统输出y(t)跟随着期望y*(t)进行变化,跟踪模型的确定方法与P(q-1)的确定方法类似。以带时延系统为例,其传递函数形式如下：

(21)

因此有：T(q-1)=GP(q-1)

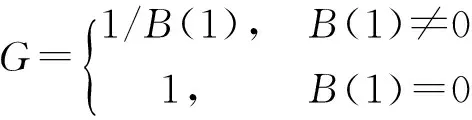
至此,RST数字控制器参数设计全部结束。完整的极点配置如图3所示。

图3 控制器设计框图

(4)验证鲁棒性裕度。

对于设计好的RST数字控制器,最后一步就是验证控制器的鲁棒性裕度,包括增益裕度(ΔG)、相角裕度(Δφ)、模值裕度(ΔM)和时延裕度(Δτ)等,其中,Δτ=Δφ/ωcr,如图4所示。

图4 系统鲁棒性裕度

3 RST数字控制器的应用

以某纸厂污泥干化中的压榨部分为系统对象,该系统为SISO结构的时延系统,辨识得到的系统传递函数为：

(22)

设采样时间Ts=1 s,加零阶保持器后离散化并进行标准化后得到:

(23)

根据二阶系统求跟踪和调节特性(两者一般不相同)。

(1)设ω0=0.5、ξ=0.9,离散化后得到跟踪特性：

(24)

(25)

控制器参数：

R(q-1)=0.8914-1.1521q-1+0.3732q-2

(26)

S(q-1)=0.2+0.0852q-1-0.0134q-2-0.0045q-3-0.1785q-4-0.0888q-5

(27)

T(q-1)=1-1.3742q-1+0.4868q-2

(28)

为了便于比较,分别使用PID控制器、PID-Smith预估控制器和RST数字控制器进行MATLAB环境下的仿真。前2个控制器均使用PID Tuner进行参数优化,得到自身最佳的控制效果；PID-Smith预估控制器采用标称情况,仿真结果如图5所示。

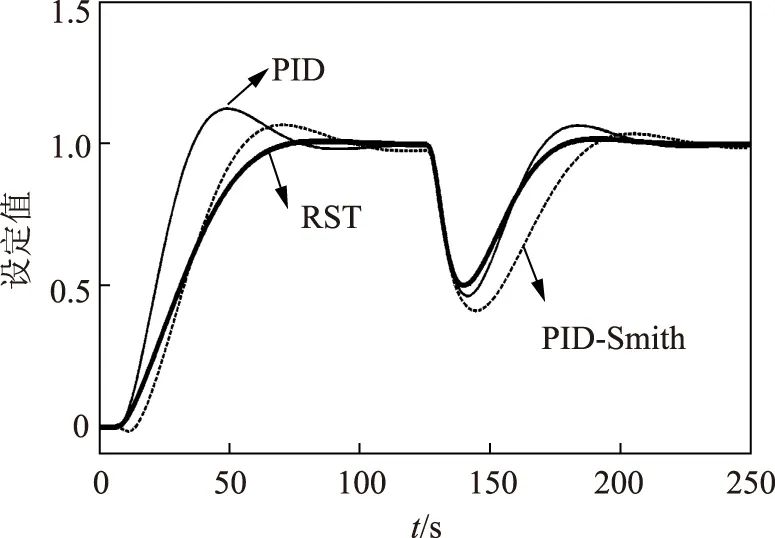
图5 3种控制器控制性能比较

粗实线代表RST数字控制器,其上升时间、调节时间和超调量都是最小的,控制效果最好；细虚线代表PID-Smith预估控制器,其整体性能较好；细实线为PID控制器,其超调量较大。跟踪性能：RST数字控制器最好,PID-Smith预估控制器次之,PID控制器最差；扰动抑制：RST数字控制器最好,PID控制器次之,PID-Smith预估控制器最差。

考虑系统的不稳定性,将对象增益扩大30%,其仿真结果如图6所示。

图6 增益扩大30%后3种控制器的鲁棒性比较

图6表明，RST数字控制器出现小幅超调,但仍然是控制性能最好的,而PID控制器和PID-Smith预估控制器均出现较大的超调量,这说明RST数字控制器的鲁棒性裕度也是最好的。根据图4求得设计的RST数字控制器的增益裕度、相角裕度和模值裕度分别为2、58和0.518。

4 结束语

本研究首先介绍了RST数字控制器结构,然后介绍了RST数字控制器参数设计步骤(包括对象模型确定、性能指标、参数求解和鲁棒性分析),最后以某纸厂污泥干化中的压榨部分为时延系统对象,并利用3种控制器(PID控制器、PID-Smith预估控制器和RST数字控制器)进行仿真对比；仿真结果表明,RST数字控制器对时延系统跟踪性能和抑制扰动性能较好,且鲁棒性较强。

[1] Carrillo F J, Rotella F. A robust adaptive controller for constant turning force regulation[J]. Control Engineering Practice, 1997, 5(12): 1673.

[2] Cuenca A, Salt J. RST controller design for a non-uniform multi-rate control system[J]. Journal of Process Control, 2012, 22(10): 1865.

[3] Khadraoui S,Nounou H N, Nounou M N, et al. A measurement-based technique for designing fixed-order RST controllers and application to a coupled water tank system[J]. Systems Science & Control Engineering: An Open Access Journal, 2014, 2(1): 484.

[4] Khadraoui S, Rakotondrabe M, Lutz P. Design of a Fixed-Order RST Controller for Interval Systems: Application to the Control of Piezoelectric Actuators[J]. Asian J Control, 2013, 15(1): 142.

[5] Mekri F, Mohamed M, Aït-Ahmed N,et al. A comparative study of voltage controllers for series active power filter[J]. Electric Power Systems Research, 2010, 80(6): 615.

[6] Bououden S, Chadli M, Karimi H R. An ant colony optimization-based fuzzy predictive control approach for nonlinear processes[J]. Information Sciences, 2015, 299(C): 143.

[7] 唐 彪. 基于模糊PID的Smith预估控制器及应用[D]. 长沙: 中南大学, 2010.

[8] 赵 青. SISO系统的数字控制研究及应用[D]. 上海: 上海交通大学, 2007.

(责任编辑：关 颖)

RST Digital Controller and Its Application in Time Delay System

LI Ming-hui SONG Zhong-zhu*XU Wen-li TAN Li-bin LI Guang-hui

(CollegeofMechanicalandElectricalEngineering,ShaanxiUniversityofScience&Technology,Xi’an,ShaanxiProvince, 710021)

(*E-mail: 342497333@qq.com)

The traditional control strategy does not focus on a problem of the robustness of the control system. The design goal of the controller is still to achieve good tracking performance and regulation performance level, and it is difficult to obtain satisfactory control effect for the time delay system. RST digital controller is a three branches structure controller which can be equivalent to a front predictor and a no delay controller, can solve the phase change of the time delay system, make the system with improved robustness. By simulation of three kinds of controllers of PID controller, PID-Smith controller and RST controller, the results show that the tracking performance and disturbance rejection performance of RST digital controller is the best, and it has strong robustness to the system with parameter uncertainty．

digital controller; time delay system; phase; robustness

2016- 03-14

李明辉,男,1972年生；博士,教授；主要研究方向：智能及高级过程控制。

*通信联系人：宋忠柱，E-mail:342497333@qq.com。

TP273;TS7

A

1000- 6842(2017)01- 0045- 05