基于偏好矩阵遗传算法求解长期车辆合乘问题

郭羽含，张美琪，周 楠

(辽宁工程技术大学 软件学院，辽宁 葫芦岛 125105)

(*通信作者电子邮箱1515120191@qq.com)

基于偏好矩阵遗传算法求解长期车辆合乘问题

郭羽含*，张美琪，周 楠

(辽宁工程技术大学 软件学院，辽宁 葫芦岛 125105)

(*通信作者电子邮箱1515120191@qq.com)

针对长期车辆合乘问题(LTCPP)，提出带有偏好矩阵的遗传算法(PMGA)，将拥有私家车且目的地相同的用户群体分配到产生总花费最少的合乘小组。首先，建立计算基于全体用户费用成本的目标函数，构建以用户时间窗和车容量为约束的长期车辆合乘模型；然后，结合模型特点，在传统遗传算法(GA)的基础上，通过在交叉算子与变异算子中添加偏好矩阵记录并更新用户间的偏好信息来提高可行解的数量和质量。实验结果表明，在相同计算环境下，当用户数量小于200时，通过PMGA所获得的20个解中的最优解的值与最优化算法相同；而处理大规模的实例时，PMGA可以获得更高质量的解。所提算法可以明显提高长期车辆合乘问题的求解质量，在降低汽车尾气污染和减少交通拥挤等方面具有重要作用。

组合优化；车辆调度问题；启发式算法；遗传算法；长期车辆合乘问题

0 引言

随着社会经济持续快速发展，我国城市私家车保有量持续大幅增长。私家车的大量使用所引发的交通拥堵、环境污染等问题日益严重[1-3]，因此车辆合乘问题成为近年来研究的热点。目前车辆合乘问题的研究多是单次车辆合乘问题，具有随机性和临时性。本文所提出的长期车辆合乘是为大中型企事业单位、政府机关设计的一种长期而固定的合乘方式，旨在减少职工上下班时驾驶的私家车道路行驶数量，进而提高城市运输效率，缓解城市交通压力。

关于车辆合乘问题的研究，多数采用依据距离将客户配对的方法，缺乏全局优化[4]。较少研究提出了全局优化的方法，如Yan等[5]提出了一种基于拉格朗日松弛的分组方法用于求解长期车辆合乘问题(Long-Term Car Pooling Problem， LTCPP)，采用网络流技术，系统地开发了一个长期的多到多的汽车模型。拉格朗日松弛方法解决模型证实了实用性模型和启发式算法在实践中是可用的。Maniezzo等[6]提出了一种蚁群优化(Ant Colony Optimization, ACO)算法和变邻域搜索结合的复合算法，提出了以时间池和车容量为约束的车模型。Barrero等[7]提出了基于量子进化算法的车辆共享模型，这种模型主要取决于电容量和车载荷量，与带有时间窗和车容量的条件意义相同。王万良等[8]在区域-区域匹配算法的基础上提出了基于交通路网的合乘路径匹配算法，对种群的大小有严格的控制，不能对现有的资源进行最优化的利用。张潜等[9]提出了基于聚类分析的多目标车辆路径优化模型，通过控制开关计算算子解决种群的复杂性。遗传算法(Genetic Algorithm, GA)作为一种被广泛应用的启发式算法，常被用来解决带有时间窗的车辆路径问题[10-12]。但现有研究对于大规模算例均存在求解效率低和质量差的问题，本文通过引入容量约束和时间窗约束构建了长期车辆合乘模型，并提出一种基于偏好矩阵的遗传算法。测试结果表明，该算法与传统的遗传算法和蚁群算法相比不仅可以提高合乘匹配的成功率，还能有效降低总体的花费成本。

1 问题的定义和描述

长期车辆合乘问题(LTCPP)假设每个合乘参与者都拥有自己的车辆，并且每个合乘参与者的上下班时间接近，其目标是将具有相同目的地的用户分为若干个合乘小组，每天轮流由组内的一名成员驾车依次接载组内其他成员共同前往工作地点，并在下班后将其依次送返。形成合乘小组后，每组的成员组合短期内将不再改变。假设如图1所示。

图1 长期车辆合乘示意图

1.1 目标函数

LTCPP是一个多目标函数问题，其目标如下：

1)最大化车辆利用率，降低往返于公共目的地的车辆数量;

2)最小化所有用户的行驶路径之和。

为降低优化难度，本文研究为单独驾车的用户引入惩罚值概念，将以上两个目标统一为求解全部出行者的总花费成本最低的单一目标函数问题。因此，LTCPP可以被转化为以下的整数规划问题。

LTCPP可以利用有向图G=(C∪{0},A)的方法来进行建模，其中：C是所有用户的集合；节点0代表其共同目的地即工作地点；集合A代表用户之间的连通路径，每条路径对应一个行驶费用cost(基于距离D)和一个行驶时间T。

设k为一组用户的集合，|k|为该组用户的数量，hp(i,k)为有向图G的一条哈密顿路径，从节点i∈k出发，通过所有节点j∈k﹨{i}，到达节点o结束。在∣k∣≤δi(δi为提供服务的组员的车容量)并满足所有用户的时间约束时，hp(i,k)是一条可行路径，最短路径min_path(i,k)即为i(i∈k)的最短可行的哈密顿路径，则一个合乘小组的费用为各位组员作为司机时所产生的成本费用之和。设costi0为一名用户直接独自驾车去工作地点的花费，pi为一名用户独自驾车的惩罚值，因此未参加任何合乘小组的用户会因惩罚而被增加额外的费用，调整惩罚值的大小可影响用户参加合乘小组时最多需额外行驶的距离。只为独自驾车的用户设置惩罚值既可使更多用户组成合乘小组，又不会鼓励将一人以上但未满员的小组合并从而使其行车成本相对合并前升高。合乘小组k的成本费用cost(k)可以被定义如下:

(1)

所有合乘小组的成本费用之和cost(σ)为：

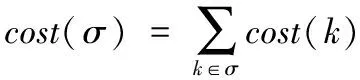
(2)

本文利用这种方法同时优化了上文提到的两个目标。

为了使更多用户可以与其他用户形成合乘小组，本文对该问题给出了惩罚值大于零的前提假设。惩罚值大于零时，只有一个用户的合成小组花费会增加，计算花费成本最低的单一问题函数问题时，为使得费用减少，可能避免只有一名用户的合成小组的情况。

1.2 数学模型

本文问题数学模型中决策变量如下：

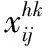
数学模型中常量如下：

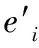
目标函数：

(3)

(4)

(5)

(6)

(7)

(8)

(9)

(10)

(11)

(12)

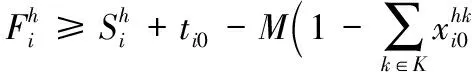
(13)

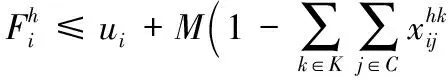
(14)

(15)

(16)

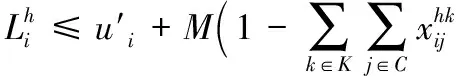
(17)

(18)

yik∈{0,1};i∈C,k∈K

(19)

ζi∈{0,1};i∈C

(20)

(21)

(22)

(23)

(24)

式(4)表示如果司机h经过i点，则将用户i加入到合乘小组K中；式(5)中的j同理；式(6)表示连续性约束；式(7)使得每个用户或者被分入一个小组或者接受惩罚；式(8)、(9)分别代表载客量和最大行程时间约束；式(10)和(12)分别限定了用户最早离家时间和最晚离家时间，其中M为一个极大常数；式(13)和(14)分别限定了最早到达工作地点时间和最晚到达工作地点时间；同样式(11)～(17)是对于用户从工作地点返回时的时间窗约束；约束条件(18)～(20)是二进制的完整性约束，同时式(21)～(24)为非负约束。

2 基于偏好矩阵的遗传算法

2.1 偏好矩阵遗传算法

由于LTCPP的时间窗较严格，经典遗传算法的交叉和变异算子的随机性会产生大量不可行解，因此算法需要花费大量时间进行修复来获得可行解。如果在每一代的遗传操作中都可以产生更多的可行解，算法的计算效率将会有很大程度的提高。为了实现这一目标，本文在传统的遗传算法基础上引入了针对长期车辆合乘问题的偏好决策机制，形成一种基于偏好矩阵的遗传算法(PreferenceMatrixbasedGeneticAlgorithm，PMGA)。

2.2 染色体编码

根据LTCPP的特点，本文采用双层编码的方法。如图2所示:第一层编码中每个数字代表每名用户的位置，d表示所有用户的共同目的地;第二层编码为一层中的用户作为司机时接载其他组员的路线和其小组内每名成员的出发时间。如第一个合乘小组中的用户1的行驶路径为1—4—6—7，出发时间为7:10,到达其他成员所在地点的时间分别为7:20、7:25和7:40。依此类推，一层中的每名用户都有其所对应的二层数据。

图2 染色体编码结构

2.3 生成初始种群

为保证生成解的多样性，本文采用随机生成个体和结构化个体的混合种群作为初始种群。

本文采用扫描法[13]生成结构化个体，以任一用户所在区位为起点，在时间窗与车容量及个体适应度值fitnessn的约束下，按顺时针方向对其他用户进行扫描分组。

2.4 选择

选择的过程是随机的，本文采用轮盘赌选择法来获得最优解。在该方法中，每个个体的选择概率与其适应度值成比例，其中个体的适应度值计算方法如下：

(25)

式(25)中的符号含义与式(3)相同。选择出的优化解通常是那些具有低费率和最低惩罚值的个体。

2.5 偏好矩阵

偏好矩阵(Preference Matrix, PM)为用于记录用户偏好信息的n×n矩阵，n为一个实例中用户的数量，矩阵中的每一个值代表一名用户愿意与另一名用户分到同一组的偏好值。每当有新的个体生成时，矩阵中的偏好信息就会被更新。

在遗传操作开始之前，需要根据用户之间的距离差和出发时间的时间差将偏好矩阵初始化，初始值initialij的计算如下：

initialij=α/dij+β/|ei+tij-ej|

(26)

其中:dij为位点i与位点j之间的距离；ei和ej为位于这两点的用户可接受的最晚离家时间；tij为位点i与位点j之间的驾驶时间；|ei+tij-ej|为用户i到用户j可接受的时间与实际从用户i到用户j的行驶时间的偏差；α和β是权衡这两部分重要程度的权重因子。

在迭代过程中，当有m个最优个体被选中时，对于被选中的个体k所包含的合乘小组中用户间的偏好值φk会通过因子ωij来增大。偏好值φk的计算如下：

(27)

2.6 偏好交叉算子

本文采用锦标赛法作为双亲的选择方案，随机地选择两个父代个体通过两点交叉法生成子代。在交叉操作过程中，每个父代的交配区域都是随机选择的。如图3所示，生成的子代1分别由父代1和父代2的交配区域交叉组合而成，其中对于交叉位点1和交叉位点2两个位点的选择必须保证一个合乘小组的完整性。当双亲中被选定的两部分基因进行重组时，剔除父代2的交配区域中与父代1中重复的基因值，然后根据偏好矩阵选择双亲交配区域以外的用户插入子代1中人数未满的合乘小组，对于交配区域外的用户i能够插入合乘小组h的偏好值preferenceih的计算如下：

(28)

其中:wik是偏好矩阵中用户i对用户k的偏好值；K为合乘小组h中所有用户的集合。

用户i被插入合乘合乘小组h中的概率pih为：

(29)

其中N为人数未满的合乘小组的集合。

子代2由父代另一部分基因区域交叉组合而成，然后与子代1作同样处理。

图3 交叉算子

2.7 偏好变异算子

在PMGA中给出了相似交换(SimilarClientExchange,S-CM)和重插入(ReinsertingCustomer,R-CM)两种变异算子。

S-CM变异算子(如图4)是随机选取n个合乘小组并在其中随机选择m个用户，根据用户的偏好信息搜索相似的用户，然后尝试将其交换。即当合乘小组h中的用户i被选中时，其他合乘小组的用户按照与合乘小组h的偏好值由大到小的顺序排列，算子将选择与i的偏好信息差异最小的用户来与i进行交换。

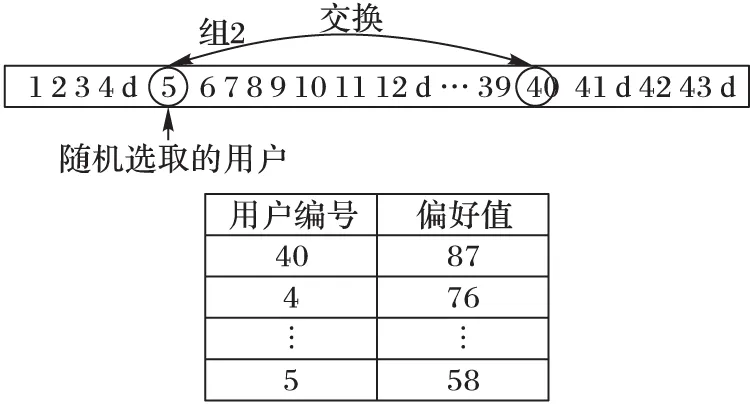
图4 SC-M变异算子

R-CM变异算子(如图5)重点研究对本组偏好值最小的用户。算子随机地选择n个合乘小组并将对自己合乘小组偏好值最小的用户在该组内剔除，这样，违反时间窗约束的用户就会在进行修复之前被移出合乘小组。然后算子根据偏好矩阵尝试将这些用户重新插入其他合乘小组。被剔除的用户被插入其他任何一个合乘小组的概率值的计算方法如式(28)～(29)。新的合乘小组可以增加解的可行性。

2.8 PMGA算法描述和分析

PMGA算法伪代码的设计如下。

输入 交叉发生的概率Pc，变异发生的概率Pm，种群规模M，终止进化的代数T，种群中个体优胜劣汰的临界值S。

输出 适应度值最大的个体Individual，适应度值最大个体的总花费成本Cost。

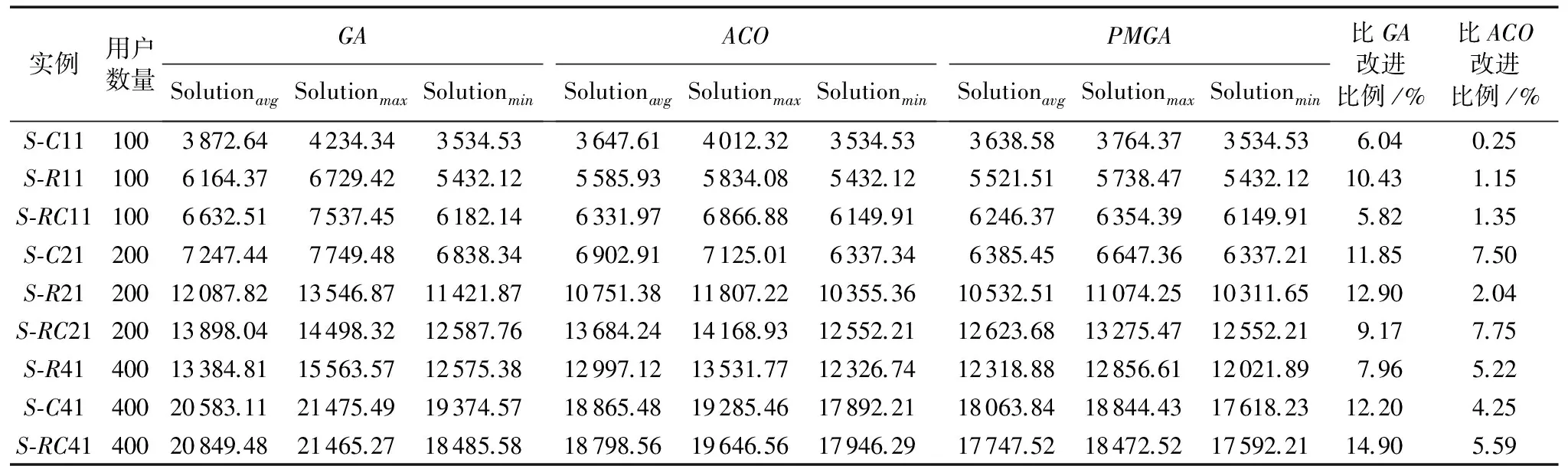
begin： 初始化Pm、Pc、M、T等参数；由概率为p的随机生成个体和扫描法生成概率为1-p的结构化个体形成第一代初始种群Pop；do{ 初始化偏好矩阵； 计算种群Population中每一个体的适应度F(i)； 初始化空种群newPopulation；do{if(random(0,1)

if(random(0,1)

{ 从n个合乘小组中选取m个用户将具有相似偏好值的用户相互交换； 在n个合乘小组中将每个合乘小组中具有最小偏好值的用户删除； 被删除的用户采用合乘小组概率值计算方法插入任何一个合乘小组； }

更新并修改偏好矩阵；

if(个体适应度值超过S)

{ 将新个体加入种群newPopulation中； }

}until(M个子代被创建)

用newPopulation取代Population；

}until(超过运行时间，或繁殖代数超过T)

找出种群中适应度值最大的个体Individual及相应的总花费；

end

图5 RC-M变异算子

PMGA采用随机和结构化的编码方式保证了解的多样性。在交叉和变异的过程中违反约束条件的用户在修复之前就能被移出合乘小组，缩短了取得可行解的时间。编码方式和采用S-CM、R-CM变异算子的变异操作增强了遗传算法跳出局部收敛的能力，以便解决调节遗传算法局部最优与收敛速度的矛盾;同时，增强了PMGA的健壮性。

3 仿真结果与分析

本文使用的24个测试实例是在硬时间窗车辆路径问题(Vehicle Routing Problem, VRP)实例的基础上修改获得的。实例中的用户分别采用三种分布方式：随机分布、群集分布以及随机和群集混合分布，分别用S-R、S-C、S-RC来表示。

3.1 测试环境

软件环境 Java虚拟机SUN JDK1.8.0_91。

硬件环境 Windows 2008系统64 bit，Intel Core2双核处理器3.2 GHz CPU，4 GB RAM。

3.2 参数配置

算法相关参数设置和仿真配置如下：种群规模为100；运行总时间为180 s；初始种群为80%结构化个体，20%随机生成个体；交叉率和变异率分别为Pc=0.8,Pm=0.1；初始偏好矩阵参数为α=0.7,β=0.3，M=10 000。对更新后的偏好矩阵，选出具有最高适应度的个体的数量为5，ωij=0.9,θ=n/300(n<300),θ=1(n≥300)，其中n为当前种群的代数；SC-M变异算子选取的用户数量m为全部用户的5%，RC-M变异算子选取的合乘小组数量n为全部合乘小组的10%，惩罚值为pi=0.5×ci0。

鉴于有限的计算资源和组合的复杂性，本文首先依据经验设定多组参数值，然后选出多组值中平均输出结果最好的一组作为最终实验参数。运行总时间代表每个算法允许执行的时间，由于不同算法生成新解的方式和每次迭代生成新解的数量不同，故使用迭代数或总生成新解数量作为终止条件无法保证比较的公平性，而以运行时间作为终止条件可以更公平地比较不同算法的求解效率和求解质量。

3.3 测试结果

本文通过对每个合乘小组中不同用户进行排列组合，最终筛选出小组内每名成员作为司机时的最短行驶路径，进而获得每个合乘小组的最短路径。由于篇幅原因，只列出用于计算机仿真实验的群集分布的100名用户的分组结果(如图6所示)及其中6个合乘小组行驶路径。

第1天 19- 37- 10- 20；14- 99- 100- 16；45- 46- 42- 69；98- 73- 70- 61；72- 71- 67- 56；59- 55- 54- 24；

第2天 37- 20- 10- 19；99- 16- 100- 14；42- 46- 45- 69；61- 98- 73- 70；71- 56- 72- 67；54- 24- 55- 59；

第3天 20- 10- 19- 37；100- 99- 14- 16；46- 45- 69- 42；73- 61- 98- 70；56- 67- 72- 71；24- 55- 54- 59；

第4天 10- 37- 20- 19；16- 99- 100- 14；69- 46- 42- 45；70- 73- 61- 98；67- 72- 71- 56；55- 59- 54- 24。

GA、ACO与PMGA在解决LTCPP时所获得的解的质量的比较如表1所示，其中Solutionavg为通过20次运行所获得的20个最优解的平均值，Solutionmax和Solutionmin分别为所获得解中的最大值和最小值。PMGA与GA、ACO算法相比，解的质量更高。

图6 群集分布种群合乘小组仿真

表1GA、ACO和PMGA成本计算结果

Tab.1CostcalculationresultsofGA,ACOandPMGA

实例用户数量GASolutionavgSolutionmaxSolutionminACOSolutionavgSolutionmaxSolutionminPMGASolutionavgSolutionmaxSolutionmin比GA改进比例/%比ACO改进比例/%S⁃C111003872．644234．343534．533647．614012．323534．533638．583764．373534．536．040．25S⁃R111006164．376729．425432．125585．935834．085432．125521．515738．475432．1210．431．15S⁃RC111006632．517537．456182．146331．976866．886149．916246．376354．396149．915．821．35S⁃C212007247．447749．486838．346902．917125．016337．346385．456647．366337．2111．857．50S⁃R2120012087．8213546．8711421．8710751．3811807．2210355．3610532．5111074．2510311．6512．902．04S⁃RC2120013898．0414498．3212587．7613684．2414168．9312552．2112623．6813275．4712552．219．177．75S⁃R4140013384．8115563．5712575．3812997．1213531．7712326．7412318．8812856．6112021．897．965．22S⁃C4140020583．1121475．4919374．5718865．4819285．4617892．2118063．8418844．4317618．2312．204．25S⁃RC4140020849．4821465．2718485．5818798．5619646．5617946．2917747．5218472．5217592．2114．905．59

从表1中可以看出，在相同的计算环境下，对于中等规模的实例如：S-C11、S-R11、S-RC11，PMGA与自适应控制优化[6]的计算结果相近；但是在处理大规模的实例如：S-C41、S-R41、S-RC41时，PMGA所获得的解的质量有了显著地提高。同时在表中还可以看到，在任何情况下PMGA所获得的解的质量都优于标准的遗传算法。通过对实验结果中平均值的比较，可以得出由PMGA所获得的实验结果与最优化算法的运算结果更接近，同时在用户数量小于200时，通过PMGA所获得的20个解中的最优解的值与最优化算法相同，而且在处理大规模的实例时，PMGA可以获得更高质量。

4 结语

本文提出的PMGA与传统遗传算法相比，获得的解的质量有了显著的提高，尤其是在处理大规模的实例时，可以通过PMGA获得更高质量的解。所以，通过实验可以得出，PMGA能够更加有效地解决LTCPP。未来的研究将会结合实际来对这一算法作更深入的评估，并进一步探索求解长期车辆合乘问题的其他算法。

)

[1]MORRISBT,TRANC,SCORAG,etal.Real-timevideo-basedtrafficmeasurementandvisualizationsystemforenergy/emissions[J].IEEETransactionsonIntelligentTransportationSystems, 2012, 13(4): 1667-1678.

[2]TERROSO-SAENZF,VALDES-VELAM,SOTOMAYOR-MAR-TINEZC,etal.AcooperativeapproachtotrafficcongestiondetectionwithcomplexeventprocessingandVANET[J].IEEETransactionsonIntelligentTransportationSystems,2012,13(2):914-929.

[3] 曹忠于.车辆合乘研究[D].上海：华东师范大学,2006:178-190.(CAOZY.Researchonvehicleride[D].Shanghai:EastChinaNormalUniversity, 2006: 178-190.)

[4]BOUKHATERCM,DAKROUBO,LAHOUDF,etal.AnintelligentandfairGAcarpoolingschedulerasasocialsolutionforgreenertransportation[C]//MELECON2014:Proceedingsofthe17thIEEEMediterraneanElectrotechnicalConference.Piscataway,NJ:IEEE, 2014: 182-186.

[5]YANS,CHENC,LINY.Amodelwithaheuristicalgorithmforsolvingthelong-termmany-to-manycarpoolingproblem[J].IEEETransactionsonIntelligentTransportationSystems, 2011, 12(4): 1362-1373.

[6]MANIEZZOV,CARBONAROA,HILDMANNH.AnANTSheuristicforthelong-termcarpoolingproblem[M]//StudiesinFuzzinessandSoftComputing,Volume141oftheSeriesStudiesinFuzzinessandSoftComputing.Berlin:Springer, 2004: 411-430.

[7]BARREROR,VANMIERLOJ,TACKOENX.Energysavingsinpublictransport[J].IEEEVehicularTechnologyMagazine, 2008, 3(3): 26-36.

[8] 王万良,黄海鹏,赵燕伟,等.基于车辆共享的软时间窗动态需求车辆路径问题[J].计算机集成制造系统,2011,17(5):1056-1063.(WANGWL,HUANGHP,ZHAOYW,etal.DynamiccustomerdemandVRPwithsofttimewindowsbasedonvehiclesharing[J].ComputerIntegratedManufacturingSystems, 2011, 17(5): 1056-1063.)

[9] 张潜,高立群,胡祥培,等.物流配送路径多目标优化的聚类—改进遗传算法[J].控制与决策，2003,18(4):418-422.(ZHANGQ,GAOLQ,HUXP,etal.Researchonmulti-objectivevehicleroutingproblemofoptimizationbasedonclusteringanalysisandimprovedgeneticalgorithm[J].ControlandDecision, 2003, 18(4):418-422.)

[10] 雷英杰.MATLAB遗传算法工具箱及应用[M].西安:西安电子科技大学出版社,2014:1-10.(LEIYJ.MATLABGeneticAlgorithmToolboxandApplication[M].Xi’an:XidianUniversityPress, 2014: 1-10.)

[11]HUANGSC,JIAUMK,LINCH.Agenetic-algorithm-basedapproachtosolvecarpoolserviceproblemsincloudcomputing[J].IEEETransactionsonIntelligentTransportationSystems, 2015, 16(1): 352-364.

[12]JIAUMK,HUANGSC.Services-orientedcomputingusingthecompactgeneticalgorithmforsolvingthecarpoolservicesproblem[J].IEEETransactionsonIntelligentTransportationSystems, 2015, 16(5): 2711-2722.

[13]GILLETTB,MILLERL.Aheuristicalgorithmforthevehicledispatchproblem[J].OperationsResearch,1974,22(2):340-349.

ThisworkissupportedbytheNaturalScienceFoundationofLiaoningProvince(2015020095).

GUO Yuhan, born in 1983, Ph.D., associate professor.His research interests include intelligent search algorithm, vehicle scheduling problem, supply chain optimization problem.

ZHANG Meiqi, born in 1991, M.S.candidate.Her research interests include supply chain optimization problem.

ZHOU Nan, born in 1994.Her research interests include vehicle scheduling problem.

Genetic algorithm with preference matrix for solving long-term carpooling problem

GUO Yuhan*, ZHANG Meiqi, ZHOU Nan

(SchoolofSoftware,LiaoningTechnicalUniversity,HuludaoLiaoning125105,China)

A Preference Matrix based Genetic Algorithm (PMGA) was introduced for solving the Long-Term Car Pooling Problem (LTCPP), and a group of users with both vehicle and the same destination was assigned to the co-generation group to minimize the total travel cost.First, the objective function of calculating the cost of all users was set up, and a long-term car pooling model with constraints of user time window and car capacity was designed.Then based on the characteristics of the model and classic Genetic Algorithm (GA), a preference matrix mechanism was adapted into the crossover and mutation operators to memorize and update the preference information among different users, thus improving the quantity and the quality of feasible solutions.The experimental results show that in the same computing environment, the optimal solution value of 20 solutions obtained by PMGA is the same as that of the exact algorithm when the number of users is less than 200.Moreover, PMGA is remarkable in solution quality when dealing with large size of instances.The proposed algorithm can significantly improve the solution quality of the long-term car pooling problem, and play an important role in reducing vehicle emission and traffic congestion.

combinational optimization; vehicle scheduling problem; heuristics algorithm; Genetic Algorithm (GA); Long-Term Car Pooling Problem (LTCPP)

2016- 08- 24;

2016- 09- 17。 基金项目:辽宁省自然科学基金资助项目(2015020095)。

郭羽含(1983—)，男，黑龙江哈尔滨人，副教授，博士，主要研究方向：智能搜索算法、车辆调度问题、供应链优化问题； 张美琪(1991—)，女，辽宁阜新人，硕士研究生，主要研究方向：供应链优化问题； 周楠(1992—)，女，辽宁朝阳人，主要研究方向：车辆调度问题。

1001- 9081(2017)02- 0602- 06

10.11772/j.issn.1001- 9081.2017.02.0602

TP399;TP

A