基于匿名广播加密的云存储访问控制方法

许盛伟，林慕清

(北京电子科技学院 信息安全研究所，北京 100070)

(*通信作者电子邮箱linmq@besti.edu.cn)

基于匿名广播加密的云存储访问控制方法

许盛伟，林慕清*

(北京电子科技学院 信息安全研究所，北京 100070)

(*通信作者电子邮箱linmq@besti.edu.cn)

针对现有的匿名广播加密方法在加解密性能和安全性方面的不足，提出一种基于拉格朗日插值多项式的匿名广播加密方法。首先定义了可以抵御自适应敌手攻击的匿名广播加密安全模型；然后在合数阶双线性群环境下采用拉格朗日插值多项式对方案进行了构建，在保证用户身份匿名性的同时，实现了高效的加解密；最后基于子群判定假设和合数阶判定双线性Diffie-Hellman假设，在标准模型下证明了方法针对自适应敌手具有密文的机密性和接收者匿名性。实验与性能分析表明，方法具有较低的通信和计算开销，可以有效地解决云存储中密文数据的匿名访问控制问题。

云存储；访问控制；匿名广播加密；拉格朗日插值多项式；合数阶双线性群

0 引言

随着计算机技术和互联网应用的迅速发展，云存储服务凭借着使用方便、节约成本等优势得到了人们的广泛关注与应用。然而，云存储在具有诸多优势的同时，也带来了许多新的安全隐患[1-3]。在云存储体系中，用户的数据存储于云服务提供商(Cloud Service Provider, CSP)的服务器上，脱离了用户的绝对控制，其安全性完全取决于CSP的系统安全性、数据管理员的素质等，这对用户来说都是不可控的因素。由于用户并不能完全信任CSP，因此当需要对数据的访问权限进行管理时，传统的由CSP所实施的访问控制方法已不再适用，因为CSP无法向用户证明自己确实正确地实施了访问控制。这时，为了保证数据的可控访问，人们往往采用基于密码学的访问控制方法，即由用户来对自己的数据进行加密，并通过控制密文数据的解密权限来实现数据的访问控制。

目前针对云存储的密文访问控制方法主要可以分为基于属性加密[4-6]和基于代理重加密[6-7]两种。这些方法分别从不同角度、针对不同场景提出了许多有效的解决方案。然而，这些方法均未考虑到对用户隐私的保护，其所产生的密文均含有授权用户的身份信息，因此并不适用于一些隐私敏感的应用场景。

与基于属性加密和代理重加密相比，广播加密[8]是一种更简单、灵活的对数据进行加密和访问控制的方法。它能够在不安全的信道(例如公共云存储服务器)上利用安全的手段来向用户共享数据，并且同时保证数据的机密性。这里的“广播”不只局限于网络通信中的广播机制，而是指广义上任何公开的信道。在广播加密方法中，数据拥有者首先选定接收者集合，然后产生针对该集合的密文。当且仅当用户属于接收者集合时，才能够正确地解密出明文；即使所有集合外的用户共谋，也无法成功进行解密。与常见的组播通信不同的是，在广播加密中，接收者集合是动态的，即它是由数据拥有者在对数据进行加密时自由选定的，并不是固定不变的。这意味着每个广播加密密文都可以具有独立的、不同的解密权限。这种特性使得广播加密可以很自然地被应用于云存储的访问控制中。

广播加密的概念由Fiat等[8]首次提出。随后研究者们针对该问题展开了一系列的研究，并取得了许多成果，其中主要可以分为基于对称密钥的广播加密[9-11]和基于公钥的广播加密[12-14]两种。基于对称密钥的方案具有较高的加解密效率，但均为集中式的方案，即只有系统中的唯一权威机构才能有权限执行加密算法。这可以满足诸如卫星电视节目的授权等领域的需求，但却不适用于文件系统的访问控制。而基于公钥的广播加密方案则较为灵活，它允许系统中的任意用户作为数据拥有者，执行加密算法来向任意接收者集合共享数据。Boneh等[14]提出的方案将双线性配对技术应用到广播加密中，提出了第一个带有常数长度的密文和私钥的完全抗共谋广播加密方案。随后，Gentry等[15]提出了具有自适应选择明文攻击(Chosen Plaintext Attack, CPA)安全性的公钥广播加密方案。该方案包括了两个广播加密方案和两个基于身份的广播加密方案，均在随机预言模型下实现了常数级的密文长度。Phan等[16]对文献[14]中的第一个方案进行了改进，提出了一种带有常数长度的密文和私钥的选择性选择密文攻击(Chosen Ciphertext Attack, CCA)安全的方案，随后他们基于双线性Diffie-Hellman指数(Bilinear Diffie-Hellman Exponent, BDHE)假设的一般化形式和KEA(Knowledge of Exponent Assumption)假设证明了该方案的自适应CCA安全性。

基于身份的广播加密(Identity-Based Broadcast Encryption, IBBE)方案是公钥广播加密方案的一种特殊形式，它使用用户的身份标识来进行加密与解密。与普通的公钥广播加密方案相比，IBBE方案在新加入用户时不需要对整个系统的公钥进行更新，因此用户可以随时加入系统。首个IBBE方案由Delerablée[17]提出，他构建了一种选择性CPA安全的IBBE方法，并具有常数长度的密文和私钥。由于方案是基于身份的，因此支持用户的动态加入，不需要更新系统公钥。Boneh等[18]使用分层身份加密结构在标准模型下构建了一个分层的广播加密方案。Zhang等[19]提出了一种基于双重加密技术的基于身份广播加密方案，使用静态假设在标准模型下实现了自适应安全性。

为了提高算法的效率，以上的这些方案往往将接收者集合以明文的形式与广播加密密文一起传送。然而在某些应用场景中，接收者的身份可能和密文本身一样都是敏感信息，此时这些方案均不再适用，因为在通信中会泄露接收者的身份信息。一些研究者们开始研究如何在加密的同时实现对接收者身份的隐藏。Barth等[20]首次提出了私有广播加密的概念，构建了两种基于公钥的方案，不会泄露关于接收者集合的任何信息。Fazio等[21]提出了一个基于子集覆盖框架的方案，具有次线性的密文长度；在该方案中，接收者的身份对于集合外的用户来说是匿名的，但对同一集合中的用户来说却是可见的。Libert等[22]首次给出了匿名广播加密(Anonymous Broadcast Encryption, ANOBE)的形式化安全模型，其允许敌手进行自适应的腐蚀攻击；然而，该方案的匿名性是由使用多份对称加密的密文构成广播体来实现的，通信开销较大。Hur等[23]构建了一种隐私保护的基于身份广播加密方案；该方案同样是选择性安全的，并且需要进行多次的解密尝试才能正确地解密出明文。

虽然针对匿名广播加密方法的研究取得了一定的进展，但目前还存在着一些不足。现有方法中解密算法的效率较低，因为现有方案所采用的方法都需要在解密时进行不断的尝试才能得到明文；另外，这些方案的安全模型均为选择性安全模型，目前还没有自适应安全的匿名广播加密方案。

本文在假定CSP为不可信实体的基础上，针对云存储访问控制中的匿名性问题，提出了一种新的匿名广播加密方法。方法采用基于身份的公钥广播加密，支持用户以身份标识直接参与运算，并且任意用户都可以调用加密算法进行数据的加密。算法在合数阶双线性群及相关复杂性假设的基础上构建，并采用拉格朗日插值多项式来实现对用户的身份信息的隐藏。与同类方案相比，本文方法在具有更高的解密效率的同时，实现了标准模型下的自适应安全性。

1 预备知识

1.1 合数阶双线性群

合数阶双线性群的概念首次在文献[24]中出现。给定安全参数k，选择两个素数p和q，令G和G分别为阶为n=pq的循环群，e:G×G→G是一个双线性映射，满足以下性质：

双线性 对于所有g,h∈G,a,b∈Zn，有e(ga,hb)=e(g,h)ab；

非退化性 存在g∈G，使得e(g,g)≠1，且是G的生成元；

可计算性 群G、G中的运算以及映射e:G×G→G的计算都可以在多项式时间内完成。

令Gp和Gq分别为阶为p和q的子群，g为群G的生成元，gp,gq分别为Gp和Gq的生成元。则对于任意hp∈Gp和hq∈Gq，元素e(hp,hq)为G中的单位元，即：

(1)

因为群G的阶为n。

1.1.1 子群判定假设

子群判定问题定义如下：给定(n,G,G,e)和一个元素x∈G，判断元素x的阶是否等于p。换句话说，在不知道阶n的因式分解的情况下，判断该元素是否属于G的一个子群。

对于一个算法来说，其解决子群判定问题的优势可以定义为概率|Pr[solved]-1/2|。如果对于任意概率多项式时间(ProbabilisticPolynomialTime,PPT)算法A来说，解决(n,G,G,e)中的子群判定问题的优势最高为一个可忽略值，则称子群判定假设(SubgroupDecisionAssumption,SDA)成立。

1.1.2 合数阶判定双线性Diffie-Hellman假设

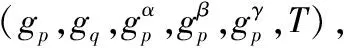
对于一个算法来说，其解决CDBDH问题的优势可以定义为概率|Pr[solved]-1/2|。如果对于任意PPT算法A来说，解决(p,q,G,G,e)中的CDBDH问题的优势最高为一个可忽略值，则称CDBDH假设成立。

1.2 拉格朗日插值多项式

拉格朗日插值[25]方法可以确定一个多项式曲线，使其精确地穿过二维平面上的一系列已知点。给定n个不同的点(x1,y1),(x2,y2),…,(xn,yn)。令n个(n-1)次的首一多项式表示为：

满足：

则插值多项式F(x)可以由以下方法给出：

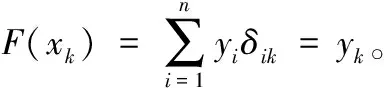
2 系统模型

为了兼顾安全性和效率，目前针对密文的访问控制方法主要采用混合加密机制来对数据进行加密，包括数据封装机制(DataEncapsulationMechanism,DEM)和密钥封装机制(KeyEncapsulationMechanism,KEM)两个部分。其中，DEM用于对具体要保护的数据文件进行加密，并且采用对称加密方法来实现较高的加解密效率；而KEM则用于对DEM中的密钥进行加密保护，主要采用公钥密码学的相关方法来实现较灵活的访问控制特性。

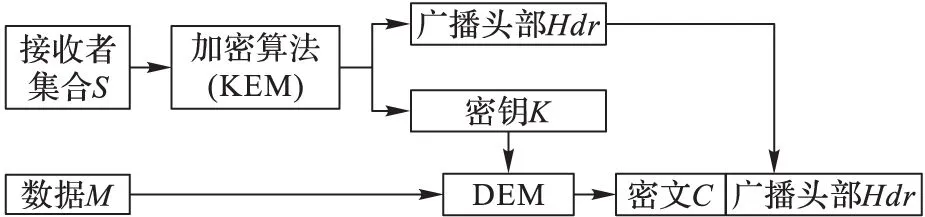
图1 广播加密中的密钥封装机制

广播加密是一种密钥封装机制。其中，用于加密数据文件的对称密钥是由加密算法输出的，如图1所示。给定一个数据文件M，数据的拥有者首先选定允许访问M的授权用户集合S，然后以S为输入执行加密算法得到一个随机的对称密钥K和一个广播头部Hdr，并使用密钥K加密数据文件M，最后将加密后的文件C与广播头部Hdr一起上传到云端。广播头部中包含了接收者的身份信息，合法的接收者可以使用自己的私钥进行解密，重新还原出对称密钥K，进而用来解密密文数据C。

本文所提出的匿名广播加密方案由三种实体构成。各种实体的角色与功能介绍如下：

1)私钥生成器(PrivateKeyGenerator,PKG)。作为系统中的一个可信的第三方，负责进行系统的初始化和密钥的生成。在生成系统的主密钥和公钥后，PKG还需要响应用户的加入请求，来为每位用户生成私钥。PKG并不参与加密与解密，如果当前没有用户需要加入的话，其可以处于离线模式，暂时停止工作。

2)数据拥有者。数据拥有者是拥有数据、并准备向指定用户共享数据的用户。在公钥广播加密系统中，任何用户都可以作为数据拥有者来向其他人共享数据。在每次加密时，数据拥有者都需要显式地指定数据的接收者集合，然后针对该集合来加密数据，得到广播密文并存储至云端。

3)接收者。接收者是在每次加密中处于目标集合中的用户，其可以使用自己的私钥来解密从云端下载的广播密文。同时，任何接收者都无法了解到集合中的其他用户身份。

实际上，数据拥有者和接收者在系统中都属于同一类型的用户。本文主要基于用户在算法中的不同角色和功能来将其划分为这两类实体。对于一个用户来说，其既可以是某个数据文件的拥有者，同时也可以是另一个数据文件的接收者。

2.1 模型的形式化定义

本文所提出的匿名广播加密方案由四个多项式时间算法组成，即ANOBE=(Setup,Join,Encrypt,Decrypt)，具体描述如下：

1)(MSK,PK)←Setup(1k)：由PKG执行，用于生成系统密钥。算法以安全参数k为输入，输出主密钥MSK和公钥PK。

2)ski←Join(MSK,IDi)：由PKG执行，用于为用户颁发私钥。算法输入主密钥MSK和用户的身份IDi，输出针对该用户的私钥ski。

3)(Hdr,K)←Encrypt(PK,S)：由数据拥有者执行，用于生成会话密钥。算法输入公钥PK和用户身份集合S={…,IDi,…}，输出广播头部Hdr和一个会话密钥K。

4)K←Decrypt(IDi,ski,Hdr)：由接收者执行，用于解密所收到的广播头部。算法输入用户身份IDi、对应该身份的私钥ski和一个广播头部，输出一个会话密钥K。

在初始化阶段中，PKG运行Setup算法来产生系统的主密钥和公钥。随后，对于每一个新用户，PKG运行Join算法来为用户生成私钥。该阶段可以看成是用户的注册阶段。只要PKG在线，新用户可以在任何时候加入系统。

给定一个要共享的数据文件M，数据拥有者首先选定一个接收者集合S，然后运行Encrypt算法来输出一个广播头部Hdr和一个会话密钥K。随后，数据拥有者可以使用对称加密算法以K为密钥对M进行加密，得到密文CM。因此最终实际存放在云端的内容为(Hdr,CM)，称为广播密文。实际上在该步骤中，数据拥有者选定的接收者集合S可以包含任意用户，甚至那些未加入系统中的用户，因为集合中只需要包含用户的身份即可。用户可以在以后的任意时刻向PKG申请私钥，然后去尝试解密消息。

对于从云端下载到的广播密文(Hdr,CM)，用户可以通过运行Decrypt算法来判断自己是否为接收者。如果该用户是接收者的话，那么Decrypt算法会输出一个正确的密钥K；如果用户不是接收者，那么算法会输出一个不确定的其他值，因此不能解密CM。与普通广播加密算法不同的是，该算法不再需要以集合S作为输入。

如果对于所有集合S和所有IDi∈S，方案满足等式：

Pr[(MSK,PK)←Setup(1k);ski←Join(MSK,IDi); (Hdr,K)←Encrypt(PK,S);K′←Decrypt(IDi,ski,Hdr):K=K′]=1

则称该匿名广播加密方案是正确的。

2.2 安全性定义

直观上，一个安全的匿名广播加密方案应该满足以下安全性质：

1)方案应该满足完全抗共谋性。给定一个广播密文，只有属于接收者集合的用户才能解密得到消息。任何集合外的用户都无法从密文中获得任何有用信息，即使所有集合外用户在一起共谋。

2)接收者的身份应该是完全匿名的。给定一个广播密文，任何用户应该只能检验自己是否为接收者，无法判断其他任何用户是否能解密，即无法确定同一集合中其他用户的身份。

本节使用挑战者C和敌手A之间的攻击实验来定义匿名广播加密方案的选择密文安全性模型。在攻击实验中，挑战者和敌手为相互交互的概率过程。该安全模型针对自适应敌手构建，相对于文献[22-23]中的静态安全模型来说，进一步提高了敌手的攻击能力。两种敌手的主要区别是，在静态敌手模型中，敌手必须首先选定想要攻击的用户集合，然后才开始进行交互实验；而在自适应敌手模型中，敌手可以在生成公钥、并完成第一阶段的质询后再选择想要进行攻击的用户集合。在这种情况下，敌手在发起挑战前所拥有的信息远多于静态敌手，因此具有更高的攻击能力。

2.2.1 密文机密性

密文的机密性指，即使敌手拥有质询所有其他用户私钥的能力，也无法区分真实的密文和一个随机给定的值。以下定义描述了方案在自适应选择密文攻击下的加密不可区分性(IND-ADA-CCA1)。

定义1IND-ADA-CCA1安全性。给定一个ANOBE方案，令A为一个自适应敌手，C为一个挑战者。考虑以下实验：

初始化 挑战者C运行Setup(1k)得到主密钥MSK和公钥PK，并将PK发送给A。

阶段1 A可以向以下两种预言机发起至多多项式次质询：

1)加入质询：对于A选择的任意身份IDi，C运行Join(MSK,IDi)得到私钥ski并发送给A。

2)解密质询：对于A选择的头部(Hdri,Si)，C随机选择一个ID∈Si，然后生成该ID的私钥sk，运行Decrypt(ID,sk,Hdri)得到Ki并发送给A。

挑战 A选择一个身份集合S*，其中集合中的身份均未在阶段1中质询过。C运行Encrypt(PK,S*)对集合S*进行加密，并得到(Hdr*,K*)。然后C选择一个随机值b∈{0,1}，并设置Kb=K*，K1-b=K′，其中K′为G中的一个随机元素。最后C将(Hdr*,K0,K1)发送给A。

阶段2 A可以继续发起至多多项式次阶段1中的加入质询，但不能针对IDi∈S*发起质询。

猜测 A输出一个针对b的猜测b′。如果b′=b，则A获胜。

2.2.2 接收者匿名性

接收者匿名性是指，给定一个密文和两个同样大小的接收者集合，敌手无法区分该密文是由哪个接收者集合通过加密算法生成的。以下定义描述了方案在自适应选择密文攻击下的匿名加密不可区分性(ANON-ADA-CCA1)。

定义2ANON-ADA-CCA1安全性。给定一个ANOBE方案，令A为一个自适应敌手，C为一个挑战者。考虑以下实验：

初始化 挑战者C运行Setup(1k)得到主密钥MSK和公钥PK，并将PK发送给A。

阶段1 A可以向以下两种预言机发起至多多项式次质询：

1)加入质询：对于A选择的任意身份IDi，C运行Join(MSK,IDi)得到私钥ski并发送给A。

2)解密质询：对于A选择的头部(Hdri,Si)，C随机选择一个ID∈Si，然后生成该ID的私钥sk，运行Decrypt(ID,sk,Hdri)得到Ki并发送给A。

挑战 A选择两个不同的接收者集合S0和S1，使两个集合的大小|S0|=|S1|，并且A未在阶段1中质询过IDi∈S0ΔS1=(S0S1)∪(S1S0)。C选择一个随机值b∈{0,1}，然后运行Encrypt(PK,Sb)对集合Sb进行加密，并得到(Hdrb,Kb)。最后C将(Hdrb,Kb)发送给A。

阶段2 A可以继续发起至多多项式次阶段1中的加入质询，但不能针对IDi∈S0ΔS1发起质询。

猜测 A输出一个针对b的猜测b′。如果b′=b，则A获胜。

3 本文方案构建

3.1 设计思路

构建方案的主要思路如下。在系统中，处于接收者集合中的每个用户都关联着一个抽象的点(x,y)。在点(x,y)中，x坐标为一个长度为l比特的大整数，代表用户的身份ID；y坐标为一个群元素，其具体的值由用户的ID值参与计算得到。显然这不是常规意义上的二维平面上的点，但并不影响对多项式的计算。每个用户的x坐标是固定的，即用户的身份不变；但y坐标在每次加密时都会发生变动，因为在计算过程中用到了随机量。

令(x1,x2,…,xn)为接收者集合中的身份。在一次加密中，数据拥有者首先选择一个随机量参与计算得到会话密钥K和每个接收者的y坐标，然后使用((x1,y1),(x2,y2),…,(xn,yn))来构造拉格朗日插值多项式：

使用拉格朗日插值多项式的主要目的是将这些y坐标隐藏到多项式中，因为只有这些值才包含了解密信息。若将某个身份xi∈(x1,x2,…,xn)代入到F(x)中进行计算的话，会得到一个对应的值yi=F(xi)。然而，如果xi∉(x1,x2,…,xn)，那么代入到F(x)中后，会产生一个不可预测的yi值，因为多项式F(x)中的系数均为群中的离散元素。这也意味着，给定多项式F(x)，无法从中恢复出点((x1,y1),(x2,y2),…,(xn,yn))。在本方案的构造中，多项式F(x)是广播头部Hdr的主要组成部分。

对于每个用户来说，用户的私钥、用户的y坐标和当前的会话密钥之间存在着联系，可以由前两个值计算出会话密钥。在这种机制下，接收者的身份对其他用户来说是隐藏的。例如，一个敌手A希望测试某个身份ID是否属于接收者集合。A可以将该ID代入到F(x)中，得到一个值y。这个y可能是正确的，但由于A并没有该ID所对应的私钥，因此无法利用该y值来计算会话密钥。也就是说，敌手A无法判断所生成的y值的正确性，即无法判断该用户是否是一个接收者。

3.2 详细算法设计

本节详细介绍本文所提出的方案中的算法。整个系统基于合数阶双线性群构建。为了表示方便，本文会同时使用乘法和加法来表示群运算。在实现时，两种运算的含义相同，均表示椭圆曲线群中的点运算。

选择适当的l值作为用户ID的长度，并选择一个长度为l的素数s来构建整数群Zs。选择哈希函数H:{0,1}*→Zs用来将任意长度的用户身份映射到Zs中。在本文接下来的内容中，均使用哈希值ID∈Zs来代表用户的身份;以l、s、H作为整个系统的公共参数，来进行具体的算法设计。

3.2.1 系统初始化算法

(MSK,PK)←Setup(1k)：进行系统的初始化和系统密钥生成。主要步骤如下：

1)选择两个长度为k的素数p和q，并生成双线性配对参数(n,G,G,e)，其中n=pq是群G和G的阶。令Gp和Gq分别为阶为p和q的子群，gp,gq分别为Gp和Gq的生成元。参数(n,G,G,e)作为公共参数公开。

3.2.2 用户加入算法

ski←Join(MSK,IDi)：为用户颁发私钥。主要步骤如下：

1)将用户的身份IDi按比特位展开成(IDi,1,…,IDi,l)，其中每个IDi, j∈{0,1}。随机选择r∈Zn，并计算私钥(这里的群运算用乘法表示)：

2)输出ski。

3.2.3 加密算法

(Hdr,K)←Encrypt(PK,S)：针对集合S进行加密并生成会话密钥。给定系统公钥PK=(gq,Q,Q,e(g1,g2))和接收者集合S=(ID1,ID2,…,ID|S|)，算法主要步骤如下：

1)对于i=1,2,…,|S|，令xi=IDi，则xi∈Zs。构造以下多项式：

使得fi(xi)=1，fi(xj)=0。其中所有运算均为在Zs中的模s运算。

2)随机选择t∈Zn，v∈Gq，(v1,v2,…,v|S|)∈Gq，计算K=e(g1,g2)t，C=v·Qt。

3)对于i=1,2,…,|S|，计算(这里的群运算用乘法表示)：

4)对于i=1,2,…,|S|，将aj,i作为大整数，计算(这里的群运算用加法表示)：

5)令Hdr=(T1,T2,…,T|S|,C),并输出(Hdr,K)。

3.2.4 解密算法

K←Decrypt(IDi,ski,Hdr)：对广播头部进行解密得到会话密钥。给定IDi，ski=(di,1,di,2)和Hdr=(T1,T2,…,T|S|,C)，算法主要步骤如下：

2)计算：

K=e(di,1,C)/e(di,2,δi)

3)输出会话密钥K。

3.3 算法的正确性

方案的正确性可以由以下推导得出：

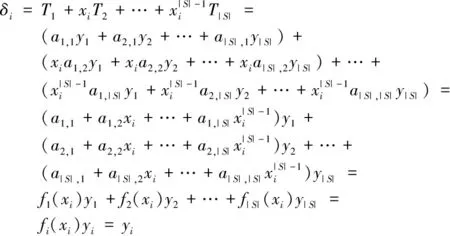
根据式(1)，对于任意元素hp∈Gp和hq∈Gq，总是存在e(hp,hq)=1。因此，在解密算法中，

实际上，在广播头部Hdr中的元组(T1,T2,…,T|S|)可以看作为拉格朗日插值多项式F(x)的系数，其中：

F(x)=T1+xT2+…+x|S|-1T|S|=f1(x)y1+f2(x)y2+…+f|S|(x)y|S|

满足F(xi)=δi=yi。

4 安全性分析

本章将对本文方案的安全性进行详细的分析与证明。在接下来的内容中，将通过构造一个挑战者C和一个敌手A之间的攻击实验来证明所提出的方案在CDBDH假设和SDA假设下针对自适应敌手的密文机密性和接收者匿名性。

4.1 密文机密性

定理1 若CDBDH假设成立，则本文所提出的ANOBE方案是IND-ADA-CCA1安全的。

证明 该安全性意味着，对于定义1中的实验，任何PPT敌手都只有最多可忽略的优势获胜。接下来的证明过程将显示，如果存在一个PPT敌手A可以以不可忽略的优势ε在实验中获胜，那么就存在一个PPT挑战者C可以以不可忽略的概率解决CDBDH问题的一个实例。换句话说，挑战者C可以借助敌手A的能力来解决CDBDH问题，因此违反了CDBDH假设。

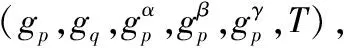
假设A可以发起最多μ次加入质询和μ′次解密质询。令l为用户身份的比特串长度。挑战者C按照以下方式和敌手A进行交互：

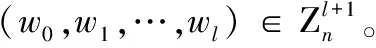
对于每位用户的身份IDi=(IDi,1,IDi,2,…,IDi,l)，定义以下三个辅助函数：

从A的角度来看，收到的这些值与从实际方案中获得的值并没有区别。

阶段1 在该阶段中，A可以向C发起两种质询。对于加入质询，C按照以下方式响应：

设A针对IDi发起质询。如果K(IDi)=0，则C终止实验并随机输出一个针对CDBDH问题的猜测θ。若K(IDi)≠0，C选择一个随机值r∈Zn，并构造私钥：

从A的角度来看，这是一个有效的私钥，因为如果令

那么有：

同时，还有：

因此该私钥ski与实际方案中的私钥具有相同的结构。当L(IDi)≠0时，该私钥是可计算的。为了便于分析，这里使用了L(IDi)≠0的充分条件K(IDi)≠0。

对于A的解密质询(Hdri,Si)，C首先为集合Si中的一个身份生成私钥，然后运行解密算法得到会话密钥Ki并发送给A。

挑战 A选择一个身份集合S*，其中集合中的身份均未在阶段1中质询过。C按以下方式对集合S*进行加密。

对于任意IDi∈S*，如果存在：

则C终止实验并随机输出一个针对CDBDH问题的猜测θ；否则，C执行以下步骤：

1)对于i=1,2,…,|S*|，令xi=IDi,构造以下多项式：

使得fi(xi)=1，fi(xj)=0。

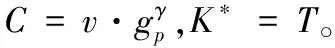
4)对于i=1,2,…,|S*|，计算：

5)令Hdr*=(T1,T2,…,T|S*|,C)，并输出(Hdr*,K*)。

如果T=e(gp,gp)αβγ，则(Hdr*,K*)是一个有效的密文，因为K*=T=e(gp,gp)αβγ=e(g1,g2)γ，并且有：

如果阶段1的解密预言机曾经向A发送过值K*，则C终止实验并随机输出一个针对CDBDH问题的猜测θ。这是因为如果发送过值K*，那么这意味着A在该阶段质询的是(Hdr*,S*)或其他有效形式，因此A可以很容易在这种情况下获胜。

相反，如果阶段1的解密预言机没有向A发送过值K*的话，那么就意味着敌手并没有从解密预言机中获得任何有用信息。这时，C选择一个随机的元素K′∈G和一个随机值b∈{0,1}，设置Kb=K*，K1-b=K′，并将(Hdr*,K0,K1)发送给A。

阶段2 A可以继续发起至多多项式次阶段1中的加入质询，但不能针对IDi∈S*发起质询。

猜测 A输出一个针对b的猜测b′。如果b′=b，则A获胜。

实验结束后，如果A获胜，则C输出针对CDBDH问题的猜测θ=1，即认为T=e(gp,gp)αβγ；反之，若A失败，则C输出针对CDBDH问题的猜测θ=0，即认为T是G中的一个其他的随机值。

分析 接下来将分析挑战者C可以解决该CDBDH问题实例的概率。

实验可能在正常结束之前就被C中止。如果发生了中止，C只有1/2的概率能解决该问题，因为中止实验后，C的猜测是随机选择的。此外，如果给定的T是G中的随机值的话，那么A的优势为0，因此无论实验中止与否，C都只有1/2的概率能解决该问题。因此CDBDH问题被解决的概率：

其中ε是A在实验中获胜的优势。接下来将讨论当T=e(gp,gp)αβγ，实验被C中止的概率。中止可能在以下三种情况下发生：

1)在加入质询中，当K(IDi)=0时；

3)在挑战阶段，当K*等于解密预言机在阶段1中回答过的某个值时。

前两种情况是相互独立的，因为敌手在进行加入质询中用到的身份与挑战阶段的接收者集合中的身份没有任何重复。将这三种情况导致的中止事件分别定义为abort1、abort2和abort3，因此有：

和：

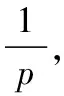
那么整个实验不中止的概率为：

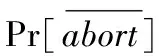
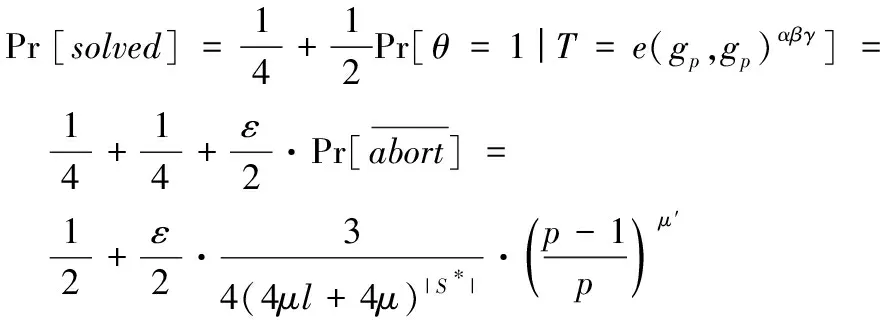
从以上分析可以看出，如果敌手在实验中获胜的优势ε是一个不可忽略的值的话，那么挑战者C同样可以以一个不可忽略的优势来解决CDBDH问题，这与CDBDH假设相矛盾。因此可以得到结论，即若CDBDH假设成立，则任何PPT敌手在该实验中获胜的优势都是一个可忽略的值，所以本文所提出的ANOBE方案是IND-ADA-CCA1安全的。

4.2 接收者匿名性

定理2 若SDA假设成立，则本文所提出的ANOBE方案是ANON-ADA-CCA1安全的。

证明 在本节中，通过定义一个实验序列0,1,2,…来对该定理进行证明。其中，实验0为原始攻击实验，即为定义2中所描述的攻击实验；令序列中的最后一个实验为目标实验，使得其中敌手的获胜概率仅为1/2。任何相邻的两个实验之间的变化都非常小，即实验i和实验i+1之间的差异对所有PPT敌手来说都是可忽略的，敌手无法区分当前进行的是实验i还是实验i+1。由于实验的总数是个常数，因此可以得出一个结论，即在原始实验中，敌手获胜的概率与1/2之间的差异也是可忽略的，从而敌手的优势为一个可忽略值。

假设A可以发起最多μ次加入质询和μ′次解密质询。定义实验序列如下：

实验0 在该实验中，挑战者C使用原始方案算法与敌手A进行交互。C首先运行Setup(1k)生成主密钥MSK和公钥PK，并将PK发送给A。在阶段1中，A可以发起两种质询。对于A的每个质询，C都运行对应的算法并将结果发送给A。在挑战阶段，C接收到A的集合S0和S1，并选择一个随机值b∈{0,1}，然后对集合Sb进行加密，得到(Hdrb,Kb)并发送给A。在阶段2，A针对IDi∉S0ΔS1继续发起加入质询，C运行Join(MSK,IDi)并返回结果。最后，A输出一个猜测b′。若b′=b则A获胜。

定义事件S0为敌手A在实验0中获胜。

实验1 在该实验中，对上述实验0进行一个微小的改动。定义实验1为：在实验0的阶段1中，令解密预言机从未向敌手A回答过Kb。

定义事件S1为敌手A在实验1中获胜。

令事件F为C在阶段1中向A应答过值Kb。如果事件F发生，则A可能会有一定的优势获胜。如果事件F没有发生的话，那么A并不能从解密预言机中获得任何有用的信息，同时实验0和实验1完全相同，有着同样的输出。即有S0∧F⟺ S1∧F。因此：

|Pr[S0]-Pr[S1]|=|Pr[S0∧F]+Pr[S0∧F]- Pr[S1∧F]-Pr[S1∧F]|= |Pr[S0∧F]-Pr[S1∧F]|≤Pr[F]

通过对定理1的证明过程可知，对于一次加密来说，K等于Kb的概率为1/p。由于A最多可以发起μ′次解密质询，因此：

|Pr[S0]-Pr[S1]|≤Pr[F]≤μ′/p

是一个可忽略的值。

实验2 在该实验中，对实验1中挑战阶段对集合Sb的加密方式进行更改。令元素(ID1,ID2,…,IDm)∈Sb为不同时存在于S0和S1中的身份，即{ID1,ID2,…,IDm}=Sb(S0∩S1)，其中1≤m≤|Sb|。为了描述方便，这里使用{ID1,…,IDm,IDm+1,…,ID|Sb|}来表示集合Sb。在加密算法的步骤3)中，增加一步判断过程，即对于i=1,2,…,|Sb|，如果1≤i≤m，则按以下方式计算yi:

否则，仍然按原来的方式来计算yi。

定义事件S2为敌手A在实验2中获胜。接下来将要说明，实验1和实验2对于敌手来说是无法区分的。

实验2中所生成的密文(Hdrb,Kb)是一个有效密文，因为经过了更改的y1,y2,…,ym是原始版本的有效变换形式。给定(Hdrb,Kb)，A可以选择一个IDi并代入到多项式中，得到一个对应的yi。根据选择的IDi的不同，可以分为以下三种情况：

1)如果其选择的IDi∈S0∩S1，那么在实验1和实验2中计算出的yi是相同的，因为都采用了同样的计算方式。

2)如果IDi∈{ID1,ID2,…,IDm}，那么A在实验1中得到的是原始版本的yi∈G；在实验2中得到的是修改过的yi∈Gp。

3)如果IDi∈S1-b且IDi∉S0∩S1，则敌手在实验1和实验2中计算出的yi都是属于群G的一个无法预测的随机值，不能用于解密，因为该IDi不是一个合法的接收者。

根据SDA假设，敌手A无法区分给定的元素是属于群G还是属于子群Gp。因此对于每个yi∈{y1,y2,…,ym}，实验1和实验2之间的差异对于A来说是可忽略的。令ε1为敌手A在SDA假设中的优势，进而有：

|Pr[S1]-Pr[S2]|≤|Sb|·ε1

也是一个可忽略的值。

实验3 在该实验中，继续对y1,y2,…,ym进行更改。在挑战阶段，对集合Sb进行加密的步骤3)中，C从群Gp中选择m个随机元素作为y1,y2,…,ym的值。其他步骤保持不变。

定义事件S3为敌手A在实验3中获胜。

主密钥中的(u0,u1,…,ul)是从Gp中随机选择的，敌手无法获知这些值。在这两个实验中，除非加密步骤2)中的随机指数t取到相同的值，否则敌手A是无法区分实验2中的原始yi和实验3中的随机yi值的。因此从A的角度看，实验2中yi和实验3中的yi是不可区分的。因此有：

|Pr[S2]-Pr[S3]|≤1/p

在实验3中，如果A将IDi∉S0∩S1代入到多项式中进行计算的话，不管该IDi是否属于集合Sb，都会得到一个随机的元素。此外，由于A不能针对IDi∈S0ΔS1发起加入质询，也就无法得到IDi对应的私钥，因此不能通过尝试解密yi来判断IDi是否属于Sb。也就是说，实验3中在挑战阶段所输出的密文(Hdrb,Kb)并不包含关于身份IDi∈S0ΔS1的任何信息。因此，

Pr[S3]=1/2

综上所述，有：

也是一个可忽略的值。敌手在原始的攻击实验中获胜的优势是一个可忽略值，因此本文所提出的ANOBE方案是ANON-ADA-CCA1安全的。

5 实验与性能分析

5.1 与现有方案的对比

本章通过与现有的匿名广播加密方案进行对比，来从理论上分析本文方案的性能和特性。分别从以下几个方面与文献[20-23]中的方案进行对比：系统公钥长度、用户私钥长度、广播密文长度和解密尝试次数。同时，还将本文方案从功能特性角度与现有方案进行了对比。其中，“任意发送者”是指允许系统中的任意用户作为数据拥有者来共享数据；“动态加入”是指用户可以在任何时刻加入系统，不需要更新系统公钥；“基于身份”是指方案支持用户使用任意比特串作为身份，而不需要为用户分配一个编号；“自适应安全性”是指方案针对自适应敌手的攻击是否是安全的。

表1给出了本文方案与现有方案的对比结果。其中：N表示系统中的总用户数，t表示在接收者集合中的用户数，r表示在文献[21]中被撤销的用户数，l表示用户身份的比特串长度，v表示群元素的长度，e表示双线性配对的长度(即G中元素的长度)，|M|表示要加密的明文消息的长度；符号“√”表示方案具有该特性，“×”表示方案无该特性。

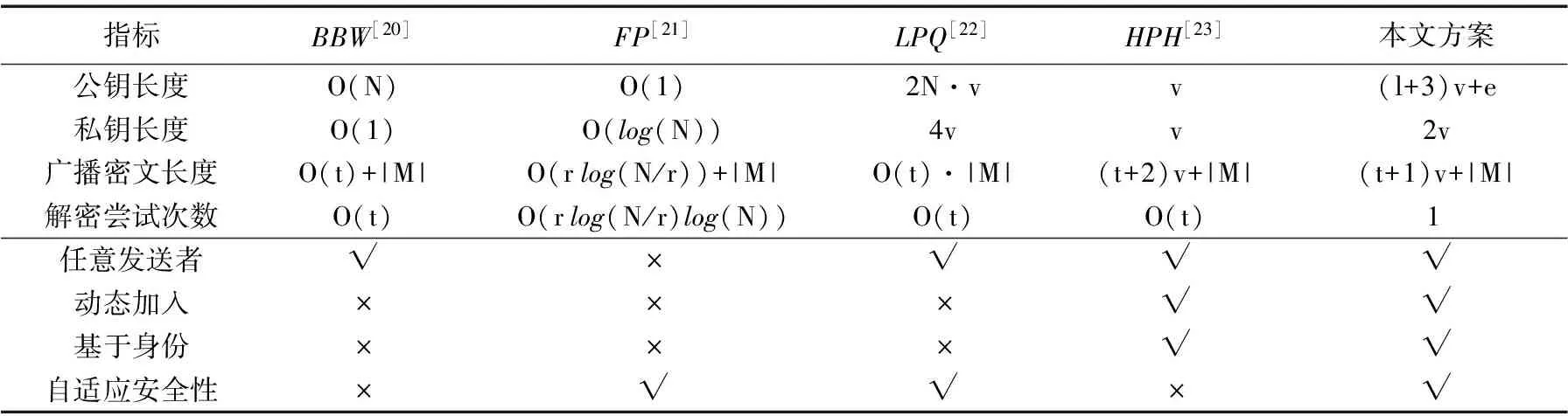
表1 几种方案的对比

由表1可以看出，与现有的匿名广播加密方案相比，本文所提出的方案只需要一次即可成功解密，而其他现有方案却需要不断地尝试才能找到正确的密文分块来解密得到明文。同时，本文所提出的方案在略微牺牲一些公钥和私钥长度的情况下，换取了最短的广播密文长度。在功能方面，与现有方案相比，本文方案实现了表中所列出的所有特性，同时在自适应敌手的攻击下是安全的。

5.2 仿真实验分析

本节通过对算法进行编码实现，并对算法的开销进行测试的方式来分析本文所提出的云存储访问控制系统在实际应用中的性能表现。

在实验中，算法采用C++语言实现，系统的安全参数为256位。使用OpenSSL库中的SHA1来对用户的身份进行处理，因此参与运算的ID串的长度为160比特。使用PBC(Pairing-BasedCryptography)库来进行群运算，包括双线性配对运算和椭圆曲线上点的指数运算。双线性群的阶为256位，其基本域的阶为512位。使用NTL(NumberTheoryLibrary)库来实现多项式环中的相关运算。算法均采用单线程的形式运行于Ubuntu14.04LTS系统下，硬件环境为IntelCorei7-2630QM, 2.0GHz，8GBRAM。

分别从通信开销和计算开销两个方面来对算法进行评估。由于广播加密算法是一种密钥封装机制，密文的最终形式为广播密文(Hdr,CM)，其中CM为使用对称加密方法所生成的密文，开销仅与明文大小、所选择的对称加密算法有关，与广播加密算法无关，因此这里不再考虑CM所产生的开销。

5.2.1 通信开销

系统中会产生额外通信开销的有系统公钥PK、每个用户的私钥ski和广播头部Hdr。其中PK和ski的大小为常数，分别为164个群元素和2个群元素；采用点压缩存储时，每个群元素占用65B，因此公钥PK和私钥ski分别占用10.7KB和130B。广播头部Hdr的大小与该次加密的目标接收者集合的大小成线性关系。分别选择从5个到50个接收者进行加密，所得到的广播头部Hdr的大小变化如图2所示。

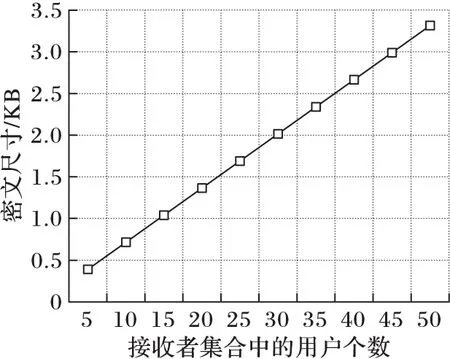
图2 密文大小与接收者数量的关系

5.2.2 计算开销

算法的初始化和用户加入两个部分的计算用时为固定值，所花费的时间与用户数量无关。同时，这两个部分在整个系统的正常工作过程中很少用到，其中初始化算法只需运行一次，用户加入算法对每个用户来说也只需运行一次,因此这里主要测试算法的加解密用时。分别随机选择5到50个接收者，执行加密算法生成密文,测试得到算法用时如图3所示。

针对图3中的密文数据，随机选择接收者集合中的一个用户，生成对应的私钥，并执行解密算法得到K。测试得到算法用时如图4所示。

由图3和图4可以看出，随着接收者集合的增大，加密与解密算法的执行时间均呈上升趋势。其中加密算法的增长速度约为二次多项式级，这与算法在理论上的开销相吻合。此外，由于应用到了拉格朗日插值多项式，解密算法的效率有很大提升，与接收者数量成线性关系，并且耗时远低于加密算法。

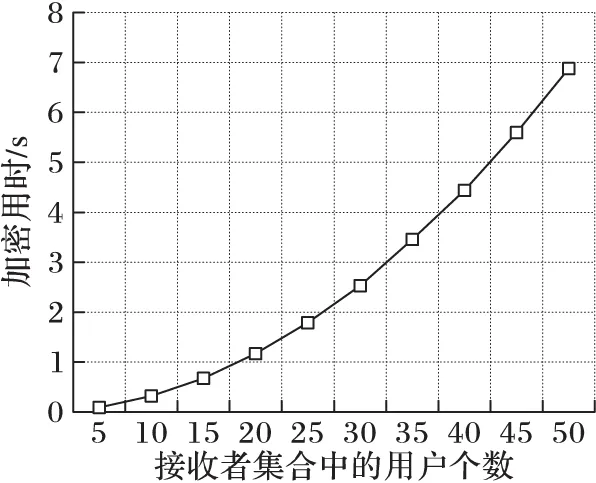
图3 加密时间与接收者数量的关系

图4 解密时间与接收者数量的关系

6 结语

匿名广播加密是广播加密方案的一个重要的衍生形式，可以在进行数据共享的过程中有效地保护接收者的隐私，因此可以广泛地应用于隐私敏感的访问控制场景中。

在匿名广播加密方案中，使用拉格朗日插值多项式可以有效地隐藏接收者的身份，同时提高解密阶段的效率。本文方案在合数阶双线性群环境下构建，具有在标准模型下针对自适应敌手攻击的密文机密性和接收者身份匿名性。与同类方案相比，本文方案同时具有了任意发送者、动态加入、基于身份等特性。对算法的仿真实验表明，本文方案是正确、高效的。作为现有针对云存储的密文访问控制方法的重要补充，本文所提出的基于匿名广播加密的访问控制方法具有广泛的实用价值和应用前景。

由于实现方法的限制，本文所构建的匿名广播加密方案为CCA1安全性，在安全模型方面仍然存在进一步改进的空间。在未来的研究计划中，可重点研究如何实现CCA2模型，以增强整体方案的安全性。同时，应考虑如何进一步提高整个系统的加解密效率，降低计算开销，以满足诸如移动互联网等低能耗场景中的应用需求。

)

[1]MATHERT,KUMARASWAMYS,LATIFS.Cloudsecurityandprivacy:anenterpriseperspectiveonrisksandcompliance[M]//CloudSecurityandPrivacy:AnEnterprisePerspectiveonRisks.Sebastopol,CA:O’ReillyMedia, 2009: 35-72.

[2] 傅颖勋,罗圣美,舒继武.安全云存储系统与关键技术综述[J].计算机研究与发展,2013,50(1):136-145.(FUYX,LUOSM,SHUJW.Surveyofsecurecloudstoragesystemandkeytechnologies[J].JournalofComputerResearchandDevelopment, 2013, 50(1): 136-145.)

[3] 李晖,孙文海,李凤华,等.公共云存储服务数据安全及隐私保护技术综述[J].计算机研究与发展,2014,51(7):1397-1409.(LIH,SUNWH,LIFH,etal.Secureandprivacy-preservingdatastorageserviceinpubliccloud[J].JournalofComputerResearchandDevelopment, 2014, 51(7): 1397-1409.)

[4]YUS,WANGC,RENK,etal.Achievingsecure,scalable,andfine-graineddataaccesscontrolincloudcomputing[C]//INFOCOM2010:Proceedingsofthe29thConferenceonInformationCommunications.Piscataway,NJ:IEEE, 2010: 1-9.

[5] 关志涛,杨亭亭,徐茹枝,等.面向云存储的基于属性加密的多授权中心访问控制方案[J].通信学报,2015,36(6):116-126.(GUANZT,YANGTT,XURZ,etal.Multi-authorityattribute-basedencryptionaccesscontrolmodelforcloudstorage[J].JournalonCommunications, 2015, 36(6): 116-126.)

[6] 洪澄,张敏,冯登国.面向云存储的高效动态密文访问控制方法[J].通信学报, 2011, 32(7): 125-132.(HONGC,ZHANGM,FENGDG.Achievingefficientdynamiccryptographicaccesscontrolincloudstorage[J].JournalonCommunications, 2011, 32(7): 125-132.)

[7] 郎讯,魏立线,王绪安,等.基于代理重加密的云存储密文访问控制方案[J].计算机应用,2014,34(3):724-727.(LANGX,WEILX,WANGXA,etal.Cryptographicaccesscontrolschemeforcloudstoragebasedonproxyre-encryption[J].JournalofComputerApplications, 2014, 34(3): 724-727.)

[8]FIATA,NAORM.Broadcastencryption[C]//CRYPTO’93:Proceedingsofthe13thAnnualInternationalCryptologyConferenceonAdvancesinCryptology,LNCS773.Berlin:Springer-Verlag, 1994: 480-491.

[9]NAORD,NAORM,LOTSPIECHJ.Revocationandtracingschemesforstatelessreceivers[C]//CRYPTO’01:Proceedingsofthe21stAnnualInternationalCryptologyConferenceonAdvancesinCryptology,LNCS2139.Berlin:Springer-Verlag, 2001: 41-62.

[10]HALEVYD,SHAMIRA.TheLSDbroadcastencryptionscheme[C]//CRYPTO’02:Proceedingsofthe22ndAnnualInternationalCryptologyConferenceonAdvancesinCryptology,LNCS2442.Berlin:Springer-Verlag, 2002: 47-60.

[11]PHANDH,POINTCHEVALD,STREFLERM.Decentralizeddynamicbroadcastencryption[CM]//SCN2012:Proceedingsofthe8thInternationalConferenceSecurityandCryptographyforNetworks,LNCS7485.Berlin:Springer-Verlag, 2012: 166-183.

[12]NAORM,PINKASB.Efficienttraceandrevokeschemes[C]//FC2000:Proceedingsofthe4thInternationalConferenceonFinancialCryptography,LNCS1962.Berlin:Springer-Verlag, 2001: 1-20.

[13]DODISY,FAZION.Publickeybroadcastencryptionforstatelessreceivers[M]//DRM2002:ProceedingsoftheACMCCS-9WorkshoponDigitalRightsManagement,LNCS2696.Berlin:Springer-Verlag, 2003: 61-80.

[14]BONEHD,GENTRYC,WATERSB.Collusionresistantbroadcastencryptionwithshortciphertextsandprivatekeys[C]//CRYPTO2005:Proceedingsofthe25thAnnualInternationalCryptologyConferenceonAdvancesinCryptology,LNCS3621.Berlin:Springer-Verlag, 2005: 258-275.

[15]GENTRYC,WATERSB.Adaptivesecurityinbroadcastencryptionsystems(withshortciphertexts) [C]//EUROCRYPT’09:Proceedingsofthe28thAnnualInternationalConferenceontheTheoryandApplicationsofCryptographicTechniques,LNCS5479.Berlin:Springer-Verlag, 2009: 171-188.

[16]PHAND-H,POINTCHEVALD,SHAHANDASHTISF,etal.AdaptiveCCAbroadcastencryptionwithconstant-sizesecretkeysandciphertexts[J].InternationalJournalofInformationSecurity, 2013, 12(4): 251-265.

[17]DELERABLÉEC.Identity-basedbroadcastencryptionwithconstantsizeciphertextsandprivatekeys[C]//ASIACRYPT2007:Proceedingsofthe13thInternationalConferenceontheTheoryandApplicationofCryptologyandInformationSecurity,LNCS4833.Berlin:Springer-Verlag, 2007: 200-215.

[18]BONEHD,HAMBURGM.Generalizedidentitybasedandbroadcastencryptionschemes[C]//ASIACRYPT2008:Proceedingsofthe14thInternationalConferenceontheTheoryandApplicationofCryptologyandInformationSecurity,LNCS5350.Berlin:Springer-Verlag, 2008: 455-470.

[19]ZHANGL,HUY,WUQ.Adaptivelysecureidentity-basedbroadcastencryptionwithconstantsizeprivatekeysandciphertextsfromthesubgroups[J].MathematicalandComputerModelling, 2012, 55(1/2): 12-18.

[20]BARTHA,BONEHD,WATERSB.Privacyinencryptedcontentdistributionusingprivatebroadcastencryption[C]//FC2006:Proceedingsofthe10thInternationalConferenceonFinancialCryptographyandDataSecurity,LNCS4107.Berlin:Springer-Verlag, 2006: 52-64.

[21]FAZION,PERERAIM.Outsider-anonymousbroadcastencryptionwithsublinearciphertexts[C]//PKC2012:Proceedingsofthe15thInternationalConferenceonPracticeandTheoryinPublicKeyCryptography,LNCS7293.Berlin:Springer-Verlag, 2012: 225-242.

[22]LIBERTB,PATERSONKG,QUAGLIAEA.Anonymousbroadcastencryption:adaptivesecurityandefficientconstructionsinthestandardmodel[C]//PKC2012:Proceedingsofthe15thInternationalConferenceonPracticeandTheoryinPublicKeyCryptography,LNCS7293.Berlin:Springer-Verlag, 2012: 206-224.

[23]HURJ,PARKC,HWANGSO.Privacy-preservingidentity-basedbroadcastencryption[J].InformationFusion, 2012, 13(4): 296-303.

[24]BONEHD,GOHE-J,NISSIMK.Evaluating2-DNFformulasonciphertexts[C]//TCC2005:ProceedingsoftheSecondTheoryofCryptographyConference,LNCS3378.Berlin:Springer-Verlag, 2005: 325-341.

[25]HILDEBRANDFB.IntroductiontoNumericalAnalysis[M].2ndedition.NewYork:DoverPublications, 1987: 25-28.

ThisworkispartiallysupportedbytheOpen-fundProjectoftheKeyLaboratoryofInformationSecurity(JBKYYWF2014KF_XSW),theDoctorialInitializingProjectofBeijingElectronicScienceandTechnologyInstitute(2016BSQD-LMQ).

XU Shengwei, born in 1976, Ph.D., associate research fellow.His research interests include information security, applied cryptography application.

LIN Muqing, born in 1987, Ph.D., assistant research fellow.His research interests include cryptography, network security.

Anonymous broadcast encryption based access control method for cloud storage

XU Shengwei, LIN Muqing*

(InformationSecurityInstitute,BeijingElectronicScienceandTechnologyInstitute,Beijing100070,China)

Focusing on the deficiencies on performance and security of the existing anonymous broadcast encryption scheme, a new anonymous broadcast encryption scheme based on the Lagrange interpolation polynomial was proposed.Firstly, an anonymous broadcast encryption security model against adaptive adversaries was defined.Then the scheme was constructed based on the Lagrange interpolation polynomial under the composite order bilinear group settings, which ensures user identity anonymity and achieves an efficient encryption and decryption at the same time.Finally, based on the subgroup decision assumption and the composite decisional bilinear Diffie-Hellman assumption, the security was proved in standard model, which shows that the proposed scheme has both ciphertext confidentiality and receiver anonymity against adaptive adversaries.Experimental results and performance analysis show that the proposed method has low communication and computing overhead, and can efficiently solve the anonymous access control issues of ciphertext data in cloud storage.

cloud storage; access control; anonymous broadcast encryption; Lagrange interpolation polynomial; composite order bilinear group

2016- 08- 29;

2016- 09- 30。 基金项目:中共中央办公厅信息安全重点实验室开放基金资助项目(基本科研业务费2014KF_XSW)；北京电子科技学院博士启动项目(2016博士启动-林慕清)。

许盛伟(1976—)，男，江西吉安人，副研究员，博士，主要研究方向：信息安全、密码应用； 林慕清(1987—)，男，安徽宿州人，助理研究员，博士，主要研究方向：密码学、网络安全。

1001- 9081(2017)02- 0473- 10

10.11772/j.issn.1001- 9081.2017.02.0473

TP309.2

A